Imagine que você está cercado por um muro infinitamente alto, mas absolutamente nada se sabe sobre o que está por trás do muro. Agora imagine que a personificação dessa parede é esta equação:
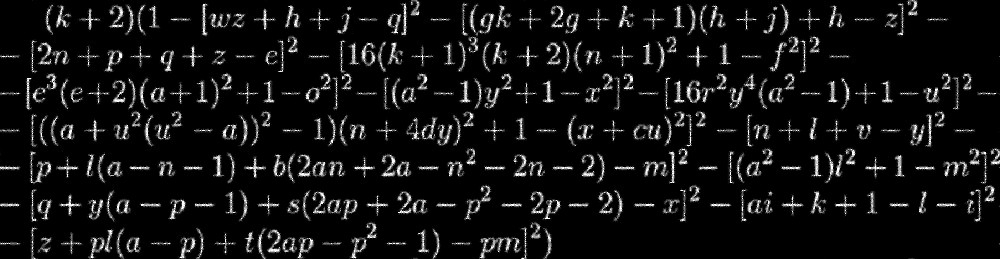
Essa metáfora será mais fácil de entender se traçarmos uma analogia com um buraco negro: não sabemos o que está sob seu horizonte de eventos e para descobrir que precisamos encontrar uma maneira de chegar lá. Algo semelhante existe no mundo da matemática. Essa equação é uma "fórmula" real de um número primo, mas, para usá-lo, precisamos descobrir como procurar por
{a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, w, v, x, y, z} .
O buraco negro e essa equação são os estados finais de algo real e abstrato. E, se houver palpites e idéias suficientes sobre o primeiro, sobre o segundo, praticamente nada se sabe. Mas, e se for realmente um buraco negro "matemático"? Você não está curioso para saber o que pode acontecer se cairmos abaixo do horizonte?
Em que consiste o muro?
Números - eles não estão no mundo real. Existem sete dados, sete átomos, sete pecados capitais, mas os sete em si não existem - é uma abstração. Sim, poderíamos dizer que os números são apenas muitos objetos abstratos, no entanto, este é um mundo inteiro. Um mundo em que, como no mundo real, existem leis. O próprio pensamento disso parece muito estranho. No entanto, a existência de um ramo da matemática como a teoria dos números sugere que essa “estranheza” é muito importante para nós.
O mais emocionante é que, entre esses objetos imaginários, existem objetos especiais - números primos. Eles são como o caos determinístico - previsíveis e imprevisíveis ao mesmo tempo, dependendo da escala de sua consideração. Por exemplo, estando ao lado deles, podemos notar que o número deles na frente de algum número arbitrário n não excederá:
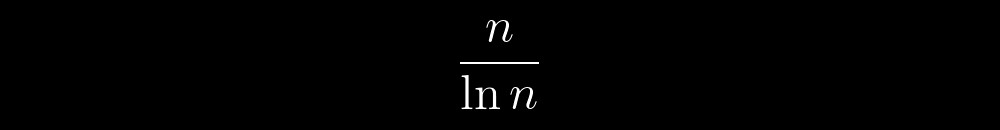
Mudando a escala, começamos a perceber muitas dicas de algum tipo de regra interna de seu comportamento. Gradualmente, essas dicas se tornam demais. Cada vez mais as perguntas “De onde elas vieram?”, “E se houver um determinado algoritmo para obter números primos?”, “E se todos os números primos puderem ser obtidos usando o mesmo algoritmo?”
Como a parede apareceu
Se uma determinada sequência de números for obtida como resultado da operação de um determinado algoritmo, o conjunto de números nessa sequência será considerado enumerável, mesmo que possa ser infinitamente grande. Conjuntos enumerados têm uma propriedade notável - diofantina. Isso significa que qualquer conjunto desse tipo pode ser representado por uma equação diofantina - um polinômio com coeficientes e potências positivas inteiras.
A declaração a seguir pode parecer completamente implausível, mas com base nessa definição, podemos argumentar que todas as chaves de segurança e valores de funções hash (mesmo bitcoins) podem ser expressos por meio de equações diofantinas. isto é equações que são resolvidas em números inteiros. E sim, teoricamente, alguém pode aprender segredos, ser uma pessoa infinitamente rica e poderosa. Mas, para se tornar uma pessoa assim, essas equações devem primeiro ser deduzidas e depois resolvidas.
O computador pode lidar com a tarefa de representar o conjunto pela equação diofantina, parcial ou completamente. Mas aqui surge outro problema - as equações diofantinas não são resolvidas de uma forma geral, ou seja, não existe um algoritmo único para resolvê-los. Isso não parece ser um grande problema, porque sabemos que algumas equações são distinguidas em formas separadas, para a solução da qual métodos eficazes já foram encontrados.
Mas, apesar da presença desses métodos, inevitavelmente encontramos dificuldades computacionais associadas à precisão dos cálculos ou à velocidade das iterações.
Como aconteceu que números primos eram enumeráveis? O próprio processo de criação de equações representando conjuntos enumeráveis se baseia nos fundamentos da matemática - aritmética e lógica. E se tivermos conhecimento suficiente sobre as propriedades dos objetos de um determinado conjunto, então, com base nesse conhecimento, podemos fazer suposições sobre o algoritmo que permite que eles sejam obtidos. E, como se viu, o conhecimento sobre as propriedades dos primos foi acumulado o suficiente para esse fim. A equação foi obtida e agora todas as questões relacionadas aos números primos são reduzidas apenas a ela.
Mas não podemos resolvê-lo.
Espessura e resistência da parede
De fato, somos desafiados. E sabemos com antecedência sobre a inevitável derrota. Talvez um retiro seja a decisão mais prudente. Mas não precisamos dessas derrotas para nos superar? Vamos tentar resolvê-lo um pouco.
Dê uma olhada na equação novamente:
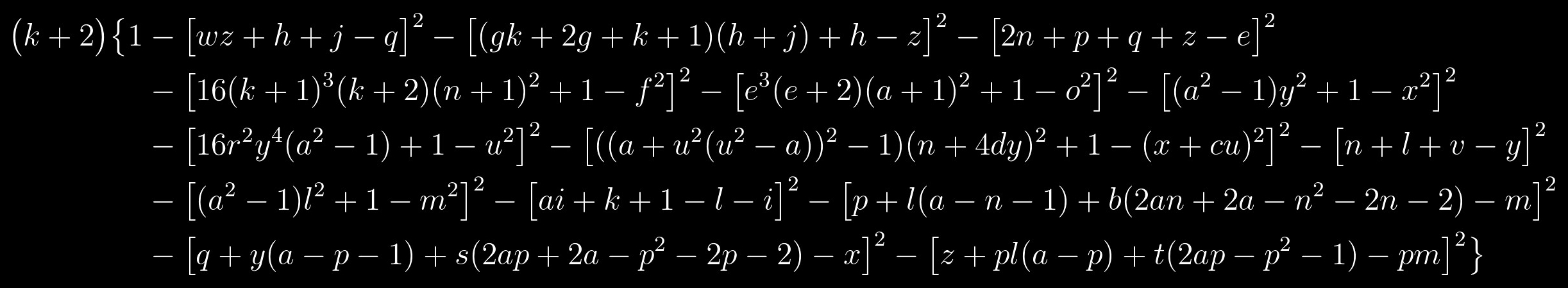
Este é um polinômio cujo conjunto de valores positivos coincide com o conjunto de primos. Consiste em dois fatores: o fator esquerdo será primo somente quando o fator direito, indicado entre colchetes, for igual a um, e isso, por sua vez, só será possível se cada termo nesse fator, indicado entre colchetes, for igual a zero . Acontece que a questão de resolver esta equação se reduz a resolver um sistema das seguintes equações:
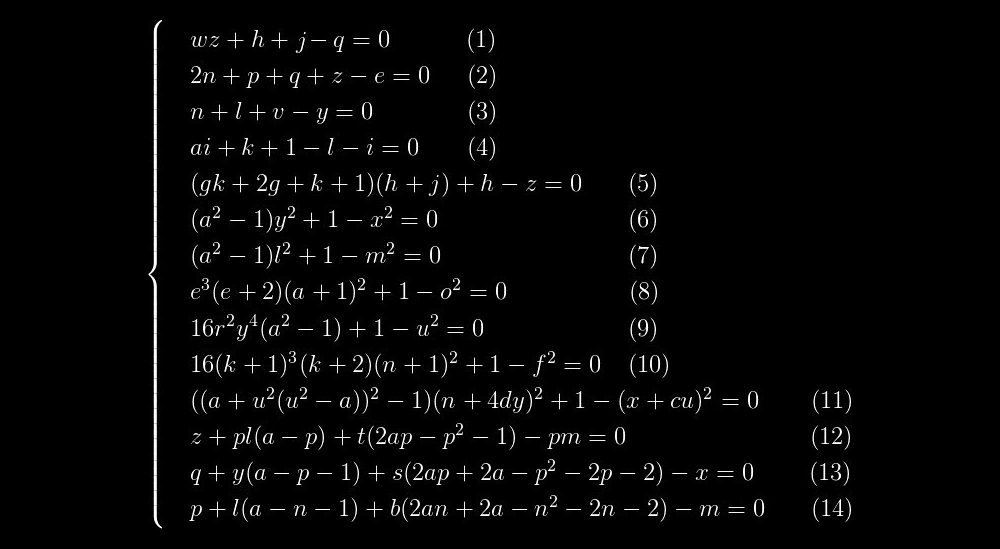
Se resolvermos esse sistema de equações e adicionarmos 2 ao valor encontrado de
k , obtemos um número primo. Mas podemos seguir o outro caminho. Pegue um número primo, subtraia 2 dele, obtendo o valor de
k , substitua-o no sistema e tente encontrar os valores das variáveis restantes em relação a ele. É dessa maneira que iremos - tente encontrar pelo menos uma solução para esse polinômio.
Todas as variáveis estão sujeitas a duas restrições estritas; elas devem ser inteiras e não podem ser negativas. Se considerarmos
k = 0 , o primeiro número primo que podemos obter é 2. Esse será o nosso ponto de partida. Depois de substituir esse valor no sistema de equações, ele assumirá a seguinte forma:
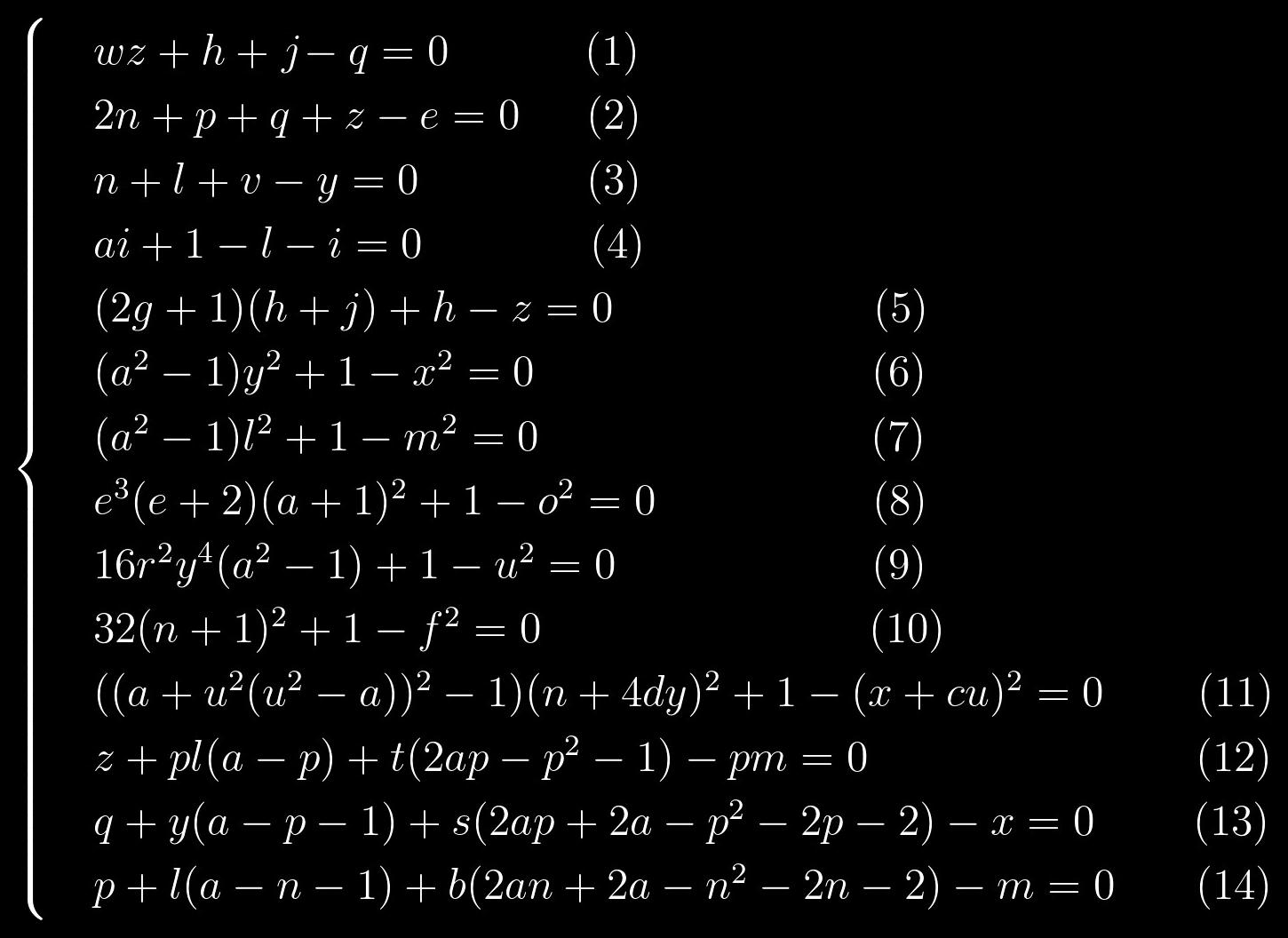
As equações (1) - (5) são equações lineares, ou seja, os graus de todas as variáveis são 1. As equações (6) - (11) têm uma estrutura muito semelhante. E finalmente, as equações (12) - (14) também se destacam em um grupo separado, e as equações (13) e (14) são semelhantes entre si, como duas gotas de água.
Podemos nos livrar de variáveis ou diminuir o grau, mas já fizemos isso antes. Uma diminuição no número de variáveis leva a um forte aumento nos graus de outras variáveis, e uma diminuição nos graus de variáveis é possível apenas através de um aumento em seu número. Então, vamos tentar resolver esse sistema neste formulário.
As equações (6) - (11) são modificações da equação de Pell:
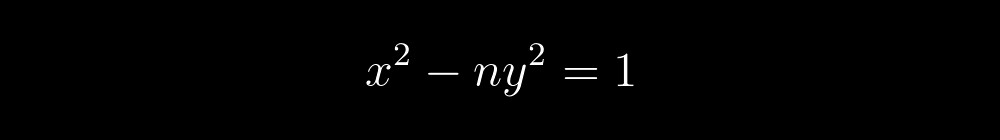
De fato, se você os reescrever assim:
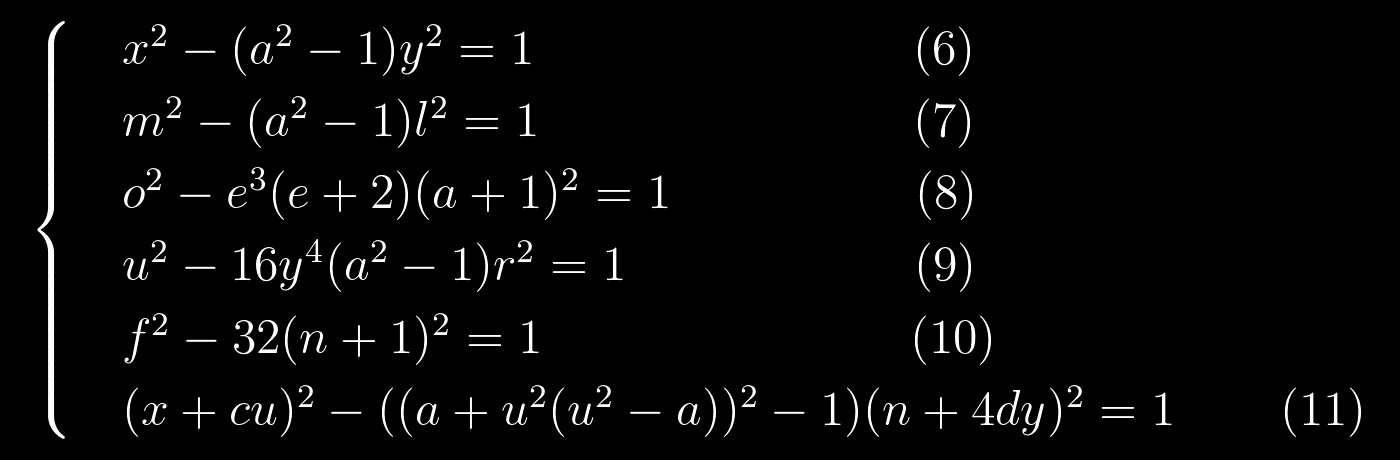
então a semelhança se torna aparente. Isso é muito encorajador, pois somos capazes de resolver as equações de Pell muito bem. Podemos tentar resolver esse sistema assim: primeiro resolvemos uma equação, substituímos suas soluções por outra, que também resolvemos e assim por diante até o fim. Parece bem simples, mas não faria mal desenhar algo como um gráfico de permutação para saber pelo menos aproximadamente em que ordem resolver as equações:
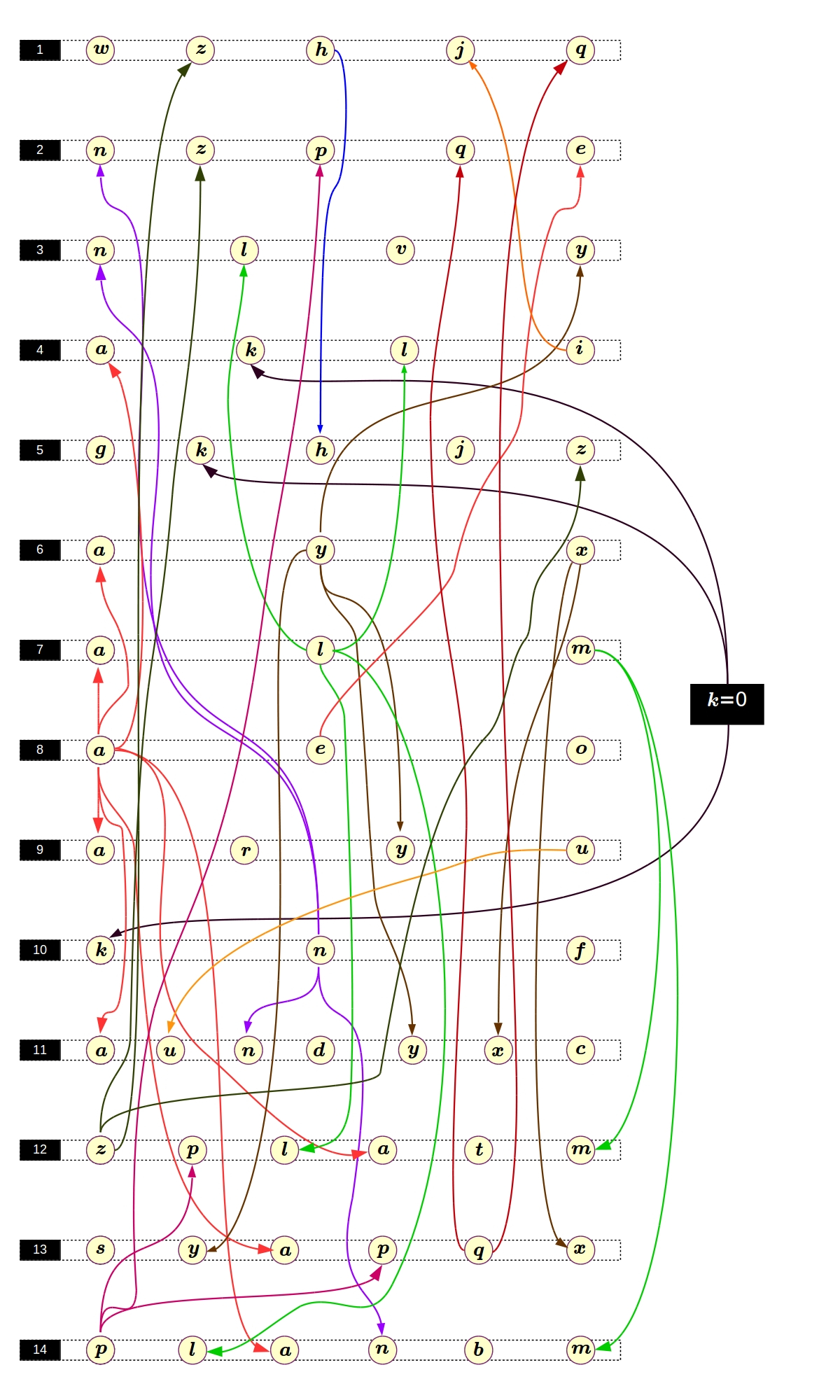
Parece que tudo é simples.
Chute na parede
Começamos com as equações de Pell. Para resolvê-los, escreveremos um pequeno script:
from decimal import * getcontext().prec = 50 def peq_dec(N): n = Decimal(N).sqrt() a = int(n) x = n - a p0, q0 = 1, 0 p1, q1 = int(a), 1 while True: a = int(1/x) x = 1/x - a p_i = a*p1 + p0 q_i = a*q1 + q0 if p_i**2 - N*q_i**2 == 1: return p_i, q_i break p0, q0 = p1, q1 p1, q1 = p_i, q_i
Graças a ele, podemos encontrar imediatamente uma solução para a equação (10)
n = 2 ,
f = 17 . No entanto, antes de prosseguir, precisamos saber algo sobre a equação de Pell.
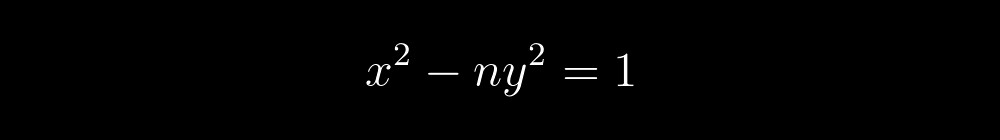
Para começar,
n não pode ser um quadrado inteiro. Além disso, qualquer equação de Pell tem um número infinito de soluções, entre as quais sempre há uma trivial:
x = 1 e
y = 0 . Cada decisão subsequente pode ser obtida com base nas anteriores, de acordo com a seguinte fórmula de recorrência:
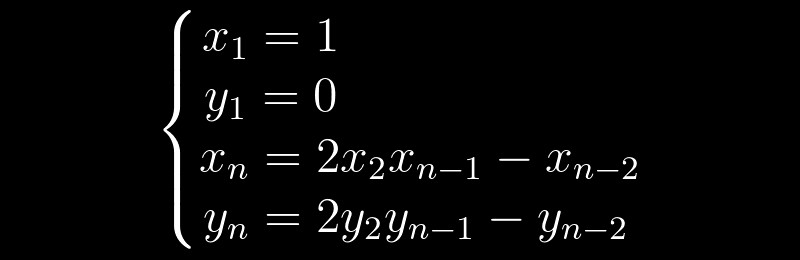
Acontece que é suficiente encontrarmos a solução mínima não trivial, e podemos fazer o resto usando um algoritmo simples. Por exemplo, para
n = 2, podemos encontrar facilmente essa solução, é
x = 3 e
y = 2 ; as soluções subseqüentes terão a seguinte aparência:
17, 12 99, 70 577, 408 3363, 2378 19601, 13860 114243, 80782 665857, 470832 3880899, 2744210 22619537, 15994428 131836323, 93222358 768398401, 543339720 4478554083, 3166815962 26102926097, 18457556052 152139002499, 107578520350 886731088897, 627013566048
Vale a pena continuar a nova decisão? Claro que vale a pena, mas ... podemos tentar prever o que está por vir.
Vamos imaginar por enquanto que estamos resolvendo um sistema de equações de três equações de Pell da seguinte forma:
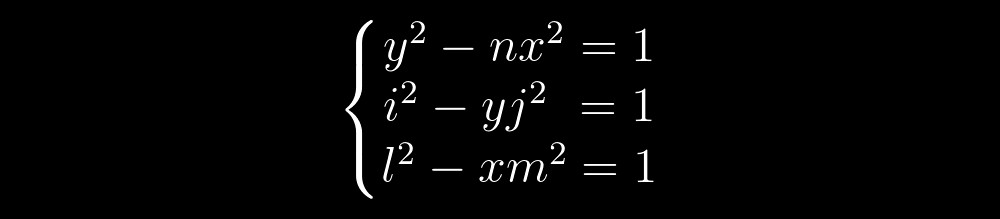
A solução para qualquer equação de Pell são os pontos da hipérbole com coordenadas inteiras. Então, podemos imaginar uma solução para as duas primeiras equações como esta:
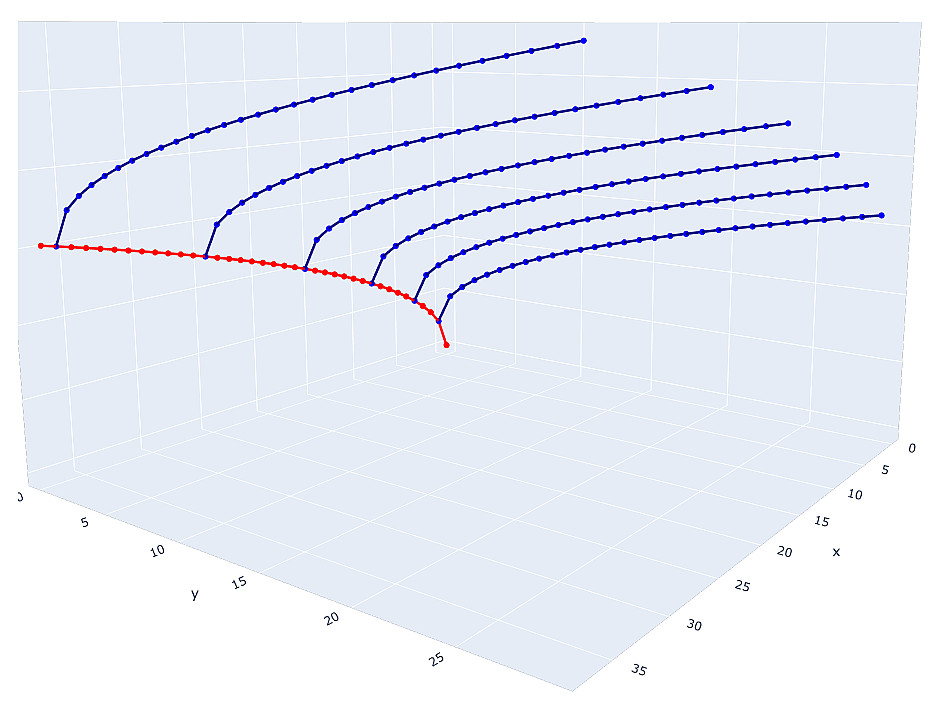
A solução para a primeira equação são os pontos inteiros da hipérbole vermelha, mas a coordenada
y de cada ponto está presente na segunda equação e pode gerar qualquer hipérbole azul cujos pontos inteiros serão a solução para a segunda equação.
Mesmo este diagrama esquemático é suficiente para entender que estamos lidando com um número muito grande de candidatos em potencial para resolver o sistema. Por que candidatos? Como alguns pontos inteiros da hipérbole serão necessariamente quadrados completos, ou seja, soluções inadequadas. E se você imagina que quaisquer condições adicionais são impostas a cada variável no sistema, encontrar candidatos para uma solução se tornará extremamente difícil. E até agora estamos falando apenas de um sistema de três equações.
Mas vamos voltar à nossa "fórmula" de números primos. O que pode estar à nossa frente?
Mais cedo ou mais tarde, descobriremos que o parâmetro
n na equação de Pell se tornará catastroficamente grande. O método de frações contínuas se tornará simplesmente inútil. Definitivamente, tentaremos outra coisa, por exemplo, enumerar valores com peneiração, de alguma forma generalizar todo o processo e chegar a algoritmos como uma peneira quadrática ou uma peneira de um campo numérico. No final, vamos nos concentrar no método "chakraval", embora ele também tenha algumas dificuldades.
Em um determinado momento, sentiremos certa confiança na solução de cada equação individual do sistema. Mas não todo o sistema. Vamos tentar aplicar alguns métodos de otimização heurística, por exemplo, um algoritmo de recozimento ou um algoritmo de formiga. Mas aqui vamos falhar. A fim de, pelo menos de alguma forma, entender as razões dessas falhas, teremos que nos aprofundar um pouco na geometria e topologia algébrica. Gradualmente, teremos uma idéia da "substância cristalizável". Podemos imaginar remotamente a estrutura da hipersuperfície sobre a qual liberamos formigas.
Com base nessas idéias, tentaremos melhorar nossos algoritmos. Para fazer isso, obteremos as melhores realizações de muitos ramos da matemática. Gradualmente, haverá menos chances nos algoritmos, mas você ainda não pode se livrar dele. O que acontecerá depois? De repente, descobrimos que muitos candidatos adequados para uma decisão verdadeira em alguns lugares são paradoxalmente densos. Cada uma dessas densidades dará esperança de que em algum lugar no centro a resposta oculta esteja oculta. Tais densidades “parecerão” formigas como algo como um hiper-funil invertido. Vamos tentar "atingir" seus centros e elevações. Mas então o que vai acontecer?
O que há atrás do muro?
Provavelmente não sei como, mas resolveremos essa equação. Talvez os computadores quânticos ou (!) Quark nos ajudem. Mas isso não se tornará um buraco na parede. Provavelmente, números primos gaussianos e uma equação ainda mais complicada que representará muitos deles nos esperarão ainda mais. Então, talvez, entre outros números hipercomplexos, encontraremos novamente algum tipo de comportamento "simples". Talvez esse seja o limite, um tipo de horizonte de eventos para um buraco negro matemático.
O que poderia estar sob esse horizonte? Provavelmente algum tipo de singularidade matemática. Provavelmente, saberemos absolutamente tudo sobre todos os conjuntos, seremos capazes de resolver quaisquer equações e quaisquer problemas. Ou talvez não haja mais perguntas e tarefas novas?
São precisamente esses pensamentos que surgem. Bem, de fato, faça qualquer pergunta sobre números primos e, graças a esta equação, você pode obter uma resposta para ela. O número de primos gêmeos é infinito? Resolva esta equação, faça alguns cálculos algébricos e obtenha a resposta. Quais são os números primos que terminam em 1, 3, 7 ou 9? O mesmo algoritmo: alguns cálculos e substituição da equação. Deseja decompor rapidamente os números em fatores primos?
Em conclusão
Conheci essa equação pela primeira vez em 2008. Nessa época, eu já estava louco por criptografia e teoria dos números, em particular o esquema RSA e o problema de fatoração. Obviamente, o polinômio que gera números primos me pareceu um tópico muito interessante, mas muito complicado. No entanto, todos os problemas que poderiam ou não ser resolvidos estavam de alguma forma relacionados com as equações diofantinas. Portanto, já em 2014, voltei-me novamente para esse polinômio, decidindo simplesmente explorar todas as seções da matemática em sequência e procurar algo que pudesse ser útil para resolvê-lo. Obviamente, não se pode falar em nenhuma cultura acadêmica de todos os meus trabalhos - nunca guardei registros sistemáticos, nunca agreguei o código gerado. Este é apenas o meu hobby.
O pensamento de escrever este artigo surgiu depois que eu vi o filme Interestelar. Eu não podia acreditar que buracos negros e gravidade pudessem ser representados de maneira tão emocionante. Mas, como se viu, o mundo "inexistente" da matemática me forneceu as mesmas impressões o tempo todo. Este mundo também tem seu próprio "espaço profundo" inacessível e suas "partículas elementares".
Com este artigo, eu queria mostrar que é possível abordar, pelo menos um pouco, qualquer tarefa mais difícil e até impossível. Existem muitas dessas tarefas e você pode escolher uma que seja do seu agrado e mais próxima da área de interesse. Obviamente, complexidade excessiva e derrota garantida privarão o menor desejo desse empreendimento. Mas todo o paradoxo é que as viagens e aventuras mais interessantes, mesmo no mundo "inexistente" da matemática, na maioria das vezes, começam dessa maneira.