Um estudo recente,
“Usando e atribuindo trechos de código do Stack Overflow em projetos do GitHub”, subitamente descobriu que, na maioria das vezes, em projetos de código aberto, minha
resposta foi escrita há quase dez anos. Ironicamente, há um erro.
Era uma vez ...
Em 2010, eu estava sentado no meu escritório e fazendo bobagens: eu me diverti com o
golfe de código e
adicionei uma classificação ao Stack Overflow.
A seguinte pergunta chamou minha atenção: como exibir o número de bytes em um formato legível? Ou seja, como converter algo como 123456789 bytes para "123,5 MB".
 Boa e velha interface de 2010, obrigado The Wayback Machine
Boa e velha interface de 2010, obrigado The Wayback MachineImplicitamente, o resultado seria um número entre 1 e 999,9 com a unidade apropriada.
Já havia uma resposta com um loop. A idéia é simples: verifique todos os graus, da unidade maior (EB = 10
18 bytes) ao menor (B = 1 byte) e aplique o primeiro, que é menor que o número de bytes. No pseudo-código, é algo parecido com isto:
suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ] magnitudes = [ 10^18, 10^15, 10^12, 10^9, 10^6, 10^3, 10^0 ] i = 0 while (i < magnitudes.length && magnitudes[i] > byteCount) i++ printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])
Geralmente, com a resposta correta com uma classificação positiva, é difícil alcançá-la. No jargão do Stack Overflow, isso é chamado de
problema do atirador mais rápido do Ocidente . Mas aqui a resposta tinha várias falhas, então eu ainda esperava superá-la. Pelo menos o código com um loop pode ser bastante reduzido.
Bem, isso é álgebra, tudo é simples!
Então me dei conta. Os prefixos são kilo-, mega-, giga-, ... - nada mais que o grau de 1000 (ou 1024 no padrão IEC); portanto, o prefixo correto pode ser determinado usando o logaritmo, e não o ciclo.
Com base nessa ideia, publiquei o seguinte:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Obviamente, isso não é muito legível e o log / pow é inferior em eficiência a outras opções. Mas como não há loop e quase nenhuma ramificação, o resultado é bastante bonito, na minha opinião.
A matemática é simples . O número de bytes é expresso como byteCount = 1000 s , onde s representa o grau (em notação binária, a base é 1024.) A solução s fornece s = log 1000 (byteCount).
Não existe um log de expressão simples 1000 na API, mas podemos expressá-lo em termos do logaritmo natural da seguinte forma s = log (byteCount) / log (1000). Em seguida, convertemos s em int; portanto, se, por exemplo, tivermos mais de um megabyte (mas não um gigabyte completo), o MB será usado como unidade de medida.
Acontece que se s = 1, a dimensão é kilobytes, se s = 2 - megabytes e assim por diante. Divida byteCount por 1000 s e coloque a letra correspondente no prefixo.
Tudo o que restou foi esperar e ver como a comunidade percebeu a resposta. Eu não conseguia pensar que esse pedaço de código se tornaria o mais amplamente divulgado na história do Stack Overflow.
Estudo de atribuição
Avanço rápido para 2018. O estudante de graduação Sebastian Baltes publica um artigo na revista científica
Empirical Software Engineering, intitulado
"Usando e atribuindo trechos de código de estouro de pilha em projetos do GitHub" . O tópico de sua pesquisa é o quanto a licença do Stack Overflow CC BY-SA 3.0 é respeitada, ou seja, os autores apontam para o Stack Overflow como uma fonte de código?
Para análise, trechos de código foram extraídos do
dump Stack Overflow e mapeados para o código nos repositórios públicos do GitHub. Citação do resumo:
Apresentamos os resultados de um estudo empírico em larga escala analisando o uso e a atribuição de fragmentos não triviais de código Java a partir de respostas SO em projetos públicos do GitHub (GH).
(Spoiler: não, a maioria dos programadores não cumpre os requisitos de licença).
O artigo possui uma tabela como esta:
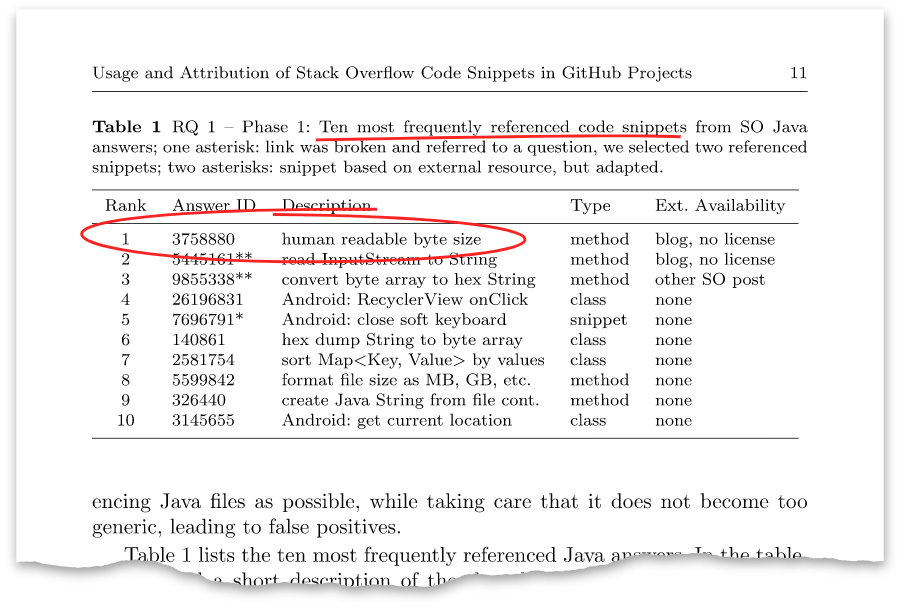
Essa resposta acima com o identificador
3758880 acabou sendo a mesma resposta que eu
publiquei oito anos atrás. No momento, ele tem mais de cem mil visualizações e mais de mil vantagens.
Uma pesquisa rápida no GitHub realmente produz milhares de repositórios com o código
humanReadableByteCount .
Procure este fragmento no seu repositório:
$ git grep humanReadableByteCount
Uma história engraçada , como descobri sobre este estudo.
Sebastian encontrou uma correspondência no repositório do OpenJDK sem nenhuma atribuição e a licença do OpenJDK não é compatível com o CC BY-SA 3.0. Na lista de discussão jdk9-dev, ele perguntou: o código de estouro de pilha é copiado do OpenJDK ou vice-versa?
O engraçado é que eu acabei de trabalhar no Oracle, no projeto OpenJDK, então meu ex-colega e amigo escreveu o seguinte:
Oi
Por que não perguntar ao autor deste post diretamente no SO (aioobe)? Ele é membro do OpenJDK e trabalhou na Oracle quando esse código apareceu nos repositórios de código-fonte do OpenJDK.
A Oracle leva esses problemas muito a sério. Sei que alguns gerentes ficaram aliviados ao lerem essa resposta e encontraram o "culpado".
Em seguida, Sebastian me escreveu para esclarecer a situação, o que eu fiz: esse código foi adicionado antes de eu ingressar na Oracle e não tenho nada a ver com o commit. É melhor não brincar com a Oracle. Alguns dias após a abertura do ticket, esse código foi excluído .
Bug
Aposto que você já pensou nisso. Que tipo de erro no código?
Mais uma vez:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Quais são as opções?
Após exabytes (10
18 ) são zettabytes (10
21 ). Talvez um número realmente grande vá além do kMGTPE? Não. O valor máximo é 2
63 -1 ≈ 9,2 × 10
18 , portanto, nenhum valor jamais excederá os exabytes.
Talvez a confusão entre unidades SI e o sistema binário? Não. Houve confusão na primeira versão da resposta, mas foi corrigida rapidamente.
Talvez exp acabe zerando, causando charAt (exp-1) travar? Também não. A primeira declaração if cobre esse caso. O valor exp será sempre pelo menos 1.
Talvez algum erro de arredondamento estranho na extradição? Bem, finalmente ...
Muitos noves
A solução funciona até se aproximar de 1 MB. Quando
"1000,0 kB" bytes são especificados como entrada, o resultado (no modo SI) é
"1000,0 kB" . Embora 999.999 esteja mais próximo de 1000 × 1000
1 que de 999.9 × 1000
1 , o significante 1000 é proibido pela especificação. O resultado correto é
"1.0 MB" .
Em minha defesa, posso dizer que, no momento da redação deste texto, havia um erro em todas as 22 respostas publicadas, incluindo as bibliotecas Apache Commons e Android.
Como consertar isso? Antes de tudo, observamos que o expoente (exp) deve mudar de 'k' para 'M' assim que o número de bytes estiver mais próximo de 1 × 1.000
2 (1 MB) do que para 999,9 × 1000
1 (999,9 k ) Isso acontece em 999.950. Da mesma forma, devemos mudar de 'M' para 'G' quando passarmos por 999.950.000 e assim por diante.
Computamos esse limite e aumentamos
exp se
bytes maior:
if (bytes >= Math.pow(unit, exp) * (unit - 0.05)) exp++;
Com essa alteração, o código funciona bem até o número de bytes se aproximar de 1 EB.
Mais nove
Ao calcular 999 949 999 999 999 999 999, o código fornece
1000.0 PB e o resultado correto é
999.9 PB . Matematicamente, o código é preciso, então o que acontece aqui?
Agora estamos diante de
double restrições.
Introdução à aritmética de ponto flutuante
De acordo com a especificação IEEE 754, valores de ponto flutuante próximos a zero têm uma representação muito densa, enquanto valores grandes têm uma representação muito esparsa. De fato, metade de todos os valores estão entre -1 e 1 e, quando se trata de números grandes, um valor do tamanho Long.MAX_VALUE não significa nada. No sentido literal.
double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true
Consulte "Bits de ponto flutuante" para obter detalhes.
O problema é representado por dois cálculos:
- Divisão em
String.format e
- Limite de expansão
exp
Podemos mudar para
BigDecimal , mas é chato. Além disso, também surgem problemas aqui, porque a API padrão não possui um logaritmo para
BigDecimal .
Reduzindo valores intermediários
Para resolver o primeiro problema, podemos reduzir o valor de
bytes para o intervalo desejado, onde a precisão é melhor, e ajustar
exp acordo. De qualquer forma, o resultado final é arredondado, portanto, não importa se jogamos fora os dígitos menos significativos.
if (exp > 4) { bytes /= unit; exp--; }
Configuração de bits menos significativos
Para resolver o segundo problema
, os bits menos significativos
são importantes para nós (99994999 ... 9 e 99995000 ... 0 devem ter graus diferentes), portanto, precisamos encontrar uma solução diferente.
Primeiro, observe que existem 12 valores limite diferentes (6 para cada modo) e apenas um deles leva a um erro. Um resultado incorreto pode ser identificado exclusivamente porque termina em D00
16 . Então você pode corrigi-lo diretamente.
long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0)) exp++;
Como contamos com certos padrões de bits nos resultados de ponto flutuante, usamos o modificador strictfp para garantir que o código funcione independentemente do hardware.
Valores de entrada negativos
Não está claro em que circunstâncias um número negativo de bytes pode fazer sentido, mas como o Java não possui um
long sem sinal, é melhor lidar com essa opção. No momento, entradas como
-10000 B produz
-10000 BVamos escrever
absBytes :
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
A expressão é tão detalhada porque
-Long.MIN_VALUE == Long.MIN_VALUE . Agora fazemos todos os cálculos de
exp usando
absBytes vez de
bytes .
Versão final
Aqui está a versão final do código, abreviada e condensada no espírito da versão original:
Observe que isso começou como uma tentativa de evitar loops e ramificações excessivas. Mas, após suavizar todas as situações de borda, o código ficou ainda menos legível que a versão original. Pessoalmente, eu não copiaria esse fragmento na produção.
Para uma versão atualizada da qualidade da produção, consulte um artigo separado:
“Formatando o tamanho do byte em um formato legível” .
Principais conclusões
- Pode haver erros nas respostas ao estouro de pilha, mesmo que tenham milhares de vantagens.
- Verifique todos os casos de limite, especialmente no código com Estouro de Pilha.
- A aritmética de ponto flutuante é complicada.
- Certifique-se de incluir a atribuição correta ao copiar código. Alguém pode levá-lo a água limpa.