1. Introdução
O artigo discute o "método Y" de montar o cubo de Rubik - é fácil de entender e lembrar. É baseado em apenas uma sequência, chamada "movimento Y". Depois de entender esse algoritmo, é improvável que você esqueça como montar o cubo.
Se você tentar pesquisar no Google as instruções de montagem do Cubo de Rubik, existem muitas opções com uma descrição da "montagem simples", inclusive na
Wikipedia . Que, em geral, são realmente bastante simples de entender, mas têm uma desvantagem significativa. Para montar um cubo, você precisa conhecer cinco ou mais seqüências não triviais (algoritmos) para reorganizar cubos individuais, para montar um cubo de Rubik em camadas. Nesse sentido, é difícil lembrar e reproduzir essas instruções independentemente. Recentemente, deparei-me acidentalmente com a menção do algoritmo “
A solução definitiva para o cubo de Rubik ”, que era fácil de lembrar e entender, e usa apenas duas seqüências. E quando comecei a descobrir com mais detalhes, também encontrei outro algoritmo - o “
método Y ”, que também é simples e usa apenas uma sequência.
Infelizmente, não encontrei uma descrição desse algoritmo em russo, por isso decidi preencher essa lacuna. Também me parece que o principal neste método é entender como ele funciona. Portanto, aqui não ofereço conjuntos de movimentos prontos para situações específicas, mas tentei descrever com mais detalhes o que está acontecendo.
As imagens neste artigo foram geradas usando a ferramenta
ruwix.com . Os links nas figuras abrirão esta ferramenta com os parâmetros correspondentes à figura. Esse é o estado descrito do cubo e você pode girá-lo com o mouse ou, em alguns casos, os movimentos descritos são especificados lá, que podem ser "perdidos" para frente e para trás.
Movimento Y
A base deste algoritmo é o movimento Y. E um componente bastante importante do algoritmo é entender a mecânica desse movimento.
Essa sequência de voltas é assim denominada porque os cubos que tocam se parecem com a letra "Y", composta de três arestas saindo de um canto do cubo.

O movimento Y é bastante simples e consiste em quatro voltas de duas faces adjacentes, por exemplo, a direita e a frente. Em uma notação de rotação comum para um cubo de Rubik, fica assim: R 'FR F'. O que pode ser descrito da seguinte maneira:
- lado direito no sentido anti-horário um quarto de volta
- face frontal no sentido horário um quarto de volta
- lado direito quarto de volta no sentido horário
- face frontal quarto de volta no sentido anti-horário
Ou seja, as faces são giradas primeiro "em direção a si mesmas" e, em seguida, na ordem inversa "a partir de si mesmas".
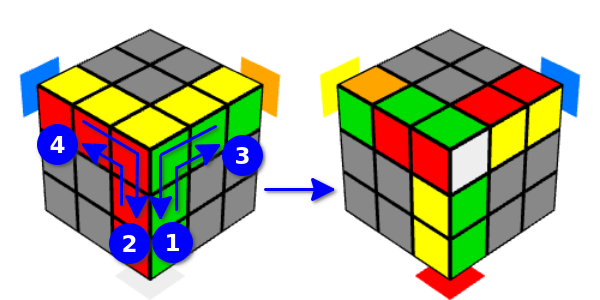
Vamos chamar essa opção de “movimento Y certo” (desde que a face seja girada pela primeira vez para a direita). Nesse caso, a posição dos cubos na aresta muda, o que é comum para essas faces e nas arestas superiores. Se você começar a girar a partir da face frontal, os mesmos cubos serão afetados, chamaremos essa opção de "movimento Y esquerdo" (uma vez que a face é girada primeiro a partir da esquerda).
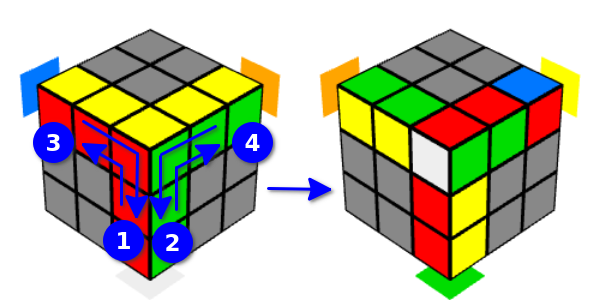
Você também pode começar com as curvas "por conta própria" - seria o mesmo se girássemos o cubo e começássemos com as curvas "por conta própria", por isso chamaremos essas opções de "movimento Y invertido direito e esquerdo". Com movimentos Y invertidos, a borda adjacente também será afetada, assim como não a parte superior, mas as bordas inferiores adjacentes a ela.
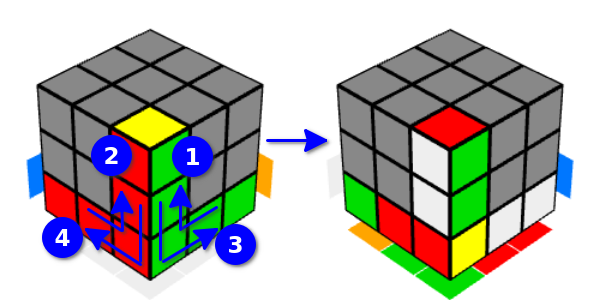
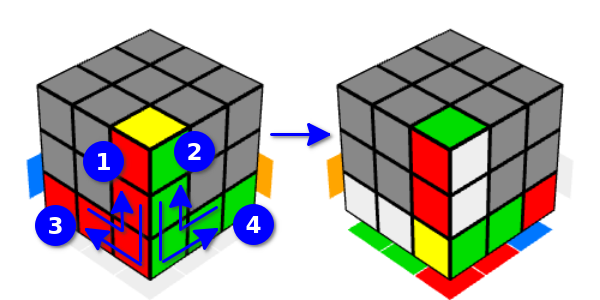
Obviamente, não há diferença fundamental em todos esses movimentos. Essa variedade é apenas para conveniência.
Listamos algumas propriedades dos movimentos Y:
- Os movimentos Y direito e esquerdo são inversos um ao outro, ou seja, a sequência de movimentos direito e esquerdo ou esquerdo e direito não alterará o estado do cubo.
- Um movimento em Y faz com que dois cubos de canto em uma face adjacente e outros dois cubos de canto mudem de lugar em um par. E três cubos localizados no meio das arestas (arestas) se movem em círculo.
- Como você pode imaginar, após dois movimentos, os cubos dos cantos retornam aos seus lugares. Mas, ao mesmo tempo, eles são transformados.
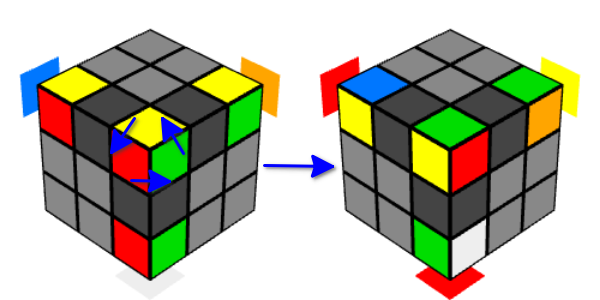
- E se você executar três vezes em dois movimentos, os cubos girarão três vezes e, como resultado, retornarão ao seu estado original.
- Os cubos da aresta retornam ao seu estado original após um ciclo de três movimentos.
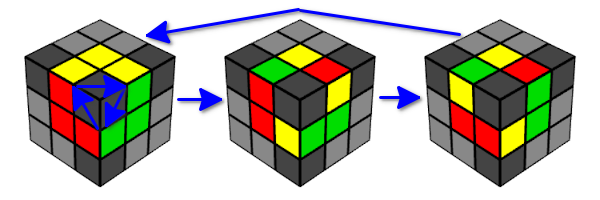
- Portanto, se você executar o movimento Y seis vezes seguidas, o estado do cubo retornará ao seu estado original.
- Após um movimento em Y, os cubos da aresta se movem na direção da primeira rotação, enquanto dois parecem rodar ao longo das faces correspondentes (ao redor do eixo), e o terceiro também gira, mas vira. O cubo que se move entre as arestas superiores, no caso do movimento Y usual (não invertido), vira. Ao trabalhar com cubos de arestas, o movimento Y ao longo das mesmas arestas pode ser feito girando o cubo em direções diferentes, alcançando assim a revolução do cubo de que precisamos.
Sequência de montagem do cubo
Primeiro, as duas camadas inferiores do cubo são montadas, com exceção de uma aresta vertical passando por essas camadas. Reservamos este lugar como um espaço de manobra. Os cubos da cruz inferior e do canto inferior são montados de maneira bastante simples, mas se houver dificuldades, não é tão difícil adaptar o movimento Y para isso ou consulte uma das instruções para uma montagem em camadas simples do cubo.

Em seguida, você precisa coletar os cubos do meio nas arestas verticais (arestas). Para fazer isso, gire a face superior com o cubo desejado para que fique em uma das faces adjacentes à aresta de destino. E também temporariamente (não se esqueça de voltar ao local) para girar a face inferior para que no lugar da borda do alvo exista um cubo, o qual deixamos especialmente desmontados. Agora você pode usar o movimento Y para mover o cubo da face superior para o local que precisamos. O movimento Y precisa ser feito para que esse cubo de aresta gire na direção certa em direção à nervura e, se necessário, vire.

Se o cubo desejado não estiver na face superior, é necessário "libertá-lo" de lá de antemão, também pelo movimento Y, sem esquecer novamente de substituir o canto desmontado na face inferior.

Até agora, reunimos as duas camadas inferiores sem uma borda. Em seguida, precisaremos coletar dois cubos de borda nas bordas superiores, que não fazem fronteira com o que não coletamos especificamente. Depois disso, dos cubos de arestas, restarão apenas três desmontados, nas arestas que formam a letra “Y”: a vertical que não coletamos e as duas arestas superiores adjacentes a ela.

E, é claro, os coletamos usando um ou mais movimentos Y, virando-os e colocando-os nos lugares certos. Aqui você só precisa levar em consideração um momento com o número de permutações, que é descrito um pouco abaixo.
Ao montar os últimos cinco cubos de aresta, podemos precisar desenrolar esta letra "Y" para fazer o movimento Y na outra direção (girando outras faces ao longo dessas arestas), conseguindo assim o movimento dos cubos de que precisamos para outros lugares com ou sem uma revolução.

Nesse ponto, teremos um cubo quase montado no qual apenas os cubos de canto na face superior e na borda vertical que não coletamos não são coletados. Usando os métodos descritos abaixo, primeiro reorganizamos os ângulos entre si para que eles estejam em seus lugares, possivelmente orientados incorretamente. E então nós os implantamos.
Viva, nosso cubo está montado!
Consideramos as permutações
O que você precisa prestar atenção quando coletamos os últimos cinco cubos de borda. Quando restarem apenas três deles, então, para que tudo dê certo com seu rearranjo na letra “Y”, é necessário que todos estejam em seus lugares (possivelmente de cabeça para baixo) ou que todos estejam fora de lugar. Isso se deve ao fato de o movimento Y reorganizar três cubos de borda simultaneamente. Se considerarmos isso do ponto de vista das trocas de cubos aos pares em locais nas bordas adjacentes, existem duas trocas (permutações). Agora deve ficar claro por que, no caso de termos exatamente dois cubos fora do lugar, não seremos capazes de coletá-los. Porque precisamos fazer uma permutação e, com a ajuda dos movimentos Y, podemos fazer apenas um número par de permutações.
O que fazer neste caso? Observe que, se você girar a face do cubo, trocamos quatro cubos de arestas ao mesmo tempo, o que será equivalente a três permutações, ou seja, um número ímpar, que é o que precisamos. A partir daí, a face superior deve estar corretamente orientada para que possamos coletar os três últimos cubos de arestas. Se os três últimos cubos da aresta exigirem uma permutação, isso significa que você precisará reorganizar os dois cubos da aresta que já estão montados na face superior em locais adjacentes.
Além disso, podemos calcular antecipadamente, antes de montar os dois primeiros cubos destes cinco, o número de permutações necessárias para colocar todos os cinco cubos de aresta no lugar. Se esse número for par, o limite superior será orientado corretamente. E se for estranho, você precisará girá-lo uma vez em qualquer direção. Assim, podemos colocar imediatamente esses dois dados nos lugares certos.
Trabalhar com cubos de canto
No último estágio da montagem, precisamos reorganizar os cubos de canto em alguns lugares e girá-los. Para fazer isso, usamos as propriedades mencionadas anteriormente do movimento Y em relação aos cubos de canto. Porque é mais conveniente trabalhar com cubos de canto localizados na face superior; para isso, usaremos o movimento Y invertido (ele começa com uma curva "para longe de você"). Nesta seção, essas opções serão usadas sem maiores esclarecimentos. Notemos imediatamente que esse movimento altera o estado de apenas um cubo na face superior - este é um cubo angular na "aresta adjacente".
Para reorganizar os cubos de canto, notamos que um único movimento Y (esquerdo e direito) troca um par de cubos de canto na "aresta adjacente" e que o uso seqüencial do movimento Y esquerdo e direito (ou direito e esquerdo) retorna o cubo inteiro no estado inicial. Vamos pensar no que acontece se girarmos a face superior entre esses movimentos. Como já vimos, na face superior apenas um cubo de canto muda, o qual é reorganizado com um cubo de par na borda. Nesse caso, teremos duas trocas de cubos de canto na borda, mas cada vez que um ângulo diferente for substituído na parte superior, e todos os outros cubos permanecerão como estavam (é claro, você ainda deve se lembrar de girar a face superior para o seu estado original). Assim, trocamos os lugares de três cubos de canto - um por baixo e dois por cima.
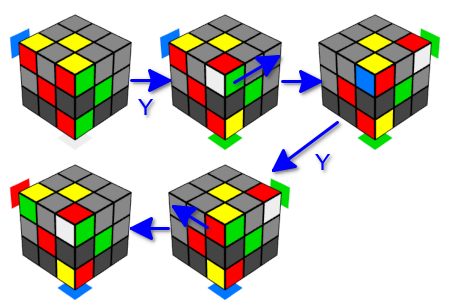
Agora vamos lidar com a rotação dos cubos. Para fazer isso, use um truque semelhante. Faremos dois movimentos Y consecutivos em uma direção. Como resultado disso, os cubos de canto permanecem no lugar, mas alteram sua orientação. Aqui estamos interessados em duas opções para uma combinação de movimentos: três movimentos duplos em uma direção (esquerda ou direita) ou movimento duplo em uma direção e movimento duplo na direção oposta. Em cada uma dessas opções, o cubo inteiro retorna ao seu estado original. E, novamente, substituiremos entre os movimentos duplos o próximo ângulo que precisamos no lugar do canto superior da “costela adjacente”. Assim, podemos girar três cubos de canto em uma face em uma direção ou dois cubos de canto em uma face em direções diferentes, sem alterar o estado dos cubos restantes. Observe que, após um movimento duplo, o cubo superior de uma nervura adjacente gira na mesma direção em que o primeiro movimento Y é realizado.
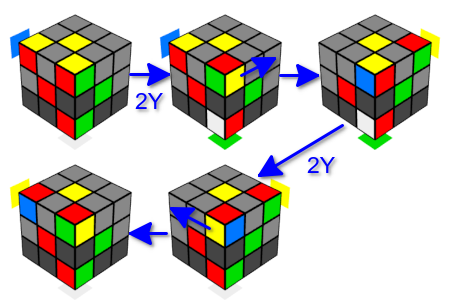
Conclusão
Não sei como será no seu caso, mas para mim a vantagem desse algoritmo não é apenas fácil de lembrar e você não precisa instruir as instruções de montagem. Mas também no fato de que agora, coletando o cubo, eu o monto, entendendo o que está acontecendo, em vez de seguir quase mecanicamente as instruções, e isso é muito mais agradável. O que eu te desejo também!