Em quase todos os jogos de cartas após o jogo, você precisa embaralhar as cartas. Enquanto embaralha as cartas, sempre surge a minha frente: "Já basta?" Essa é uma pergunta séria: não quero gastar muito tempo e jogar em um deck carregado também não é divertido.

O artigo irá lidar com a situação.

Shuffle Way

Existem maneiras legais de baralhar as cartas, aleatoriamente, por exemplo.

Não sei como, e os cartões de papelão não podem ser embaralhados assim, então embaralha de uma maneira simples, é algo parecido com isto:

Primeiro, separo a parte do convés, depois jogo a parte dessa parte para o outro lado e, em seguida, relato a parte restante. De acordo com minhas observações, as pessoas embaralham as cartas exatamente dessa maneira ou próximas a ela. Em geral, ele pode ser dividido em um número maior de partes, mas essas já são detalhes. No artigo, analisaremos esse método de reprodução aleatória.

O que é o layout aleatório do cartão?

A primeira coisa que me ocorreu foi que, com um bom layout, qualquer cartão pode estar igualmente no i-ésimo lugar.

Mas isso não é suficiente. Por exemplo, se você cortar o baralho - divida-o em dois em um local aleatório e troque-o -, a primeira carta poderá ter qualquer chance. Mas, ao mesmo tempo, esse é obviamente um layout ruim: depois de cada cartão, exceto por alguns, o mesmo cartão será colocado antes do "corte". Ou seja, os jogadores receberão cartas "correlacionadas". No caso de um tolo, um será espancado, e o outro será espancado, e isso não será acidental.

Outra abordagem para determinar um bom layout é que, no i + 1º lugar, há um cartão independente do cartão no i-ésimo lugar. Você pode imaginar desta maneira: se você olhar para a carta do topo do baralho, não poderá adivinhar qual carta será a próxima.

Essa abordagem também pode ter problemas que são resolvidos considerando-se grandes distribuições conjuntas, mas, para a análise atual, será completamente adequado para nós.

Como medir a "bondade" do layout

Pegamos o baralho que sobrou do jogo anterior. Nós numeramos todos os cartões em ordem. A má situação é quando, depois de embaralhar em algum lugar após o cartão com o número i, há um cartão com o número i + 1. Portanto, mediremos a proporção de cartões que estão em ordem após o embaralhamento.

def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total 

É claro que, mesmo em um baralho bem baralhado, algumas cartas caem aleatoriamente em ordem. Sua parte será em média 1 / (n-1), onde n é o número de cartas no baralho.

Resultados

Calculamos a probabilidade de cartas consecutivas para um baralho de 52 cartas, dependendo do número de iterações mistas.

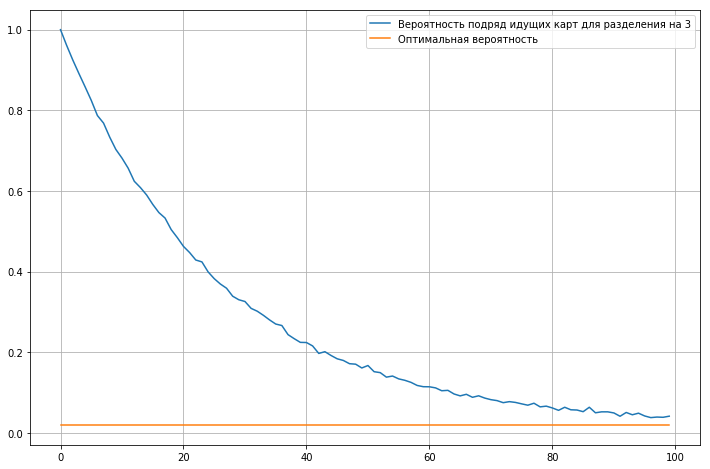
O gráfico mostra que, mesmo após centenas de iterações, a probabilidade de cartões consecutivos é cerca de duas vezes maior que a probabilidade ideal.

 import random def two_split_shuffle(a): s1 = random.randint(1,len(a)-1) s2 = random.randint(1,len(a)-1) s_min = min(s1, s2) s_max = max(s1, s2) p1 = a[:s_min] p2 = a[s_min:s_max] p3 = a[s_max:] return p3 + p2 + p1 def shuffle_n(a, f, n): for _ in range(n): a = f(a) return a def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total def expected(f, n = 100): s = 0 for _ in range(n): s += f() return s / n def get_expected_next_stat(shuf, n, cards): return expected(lambda: next_stat(shuffle_n(range(cards), shuf, n))) cards = 52 x = range(100) y = map(lambda i: get_expected_next_stat(two_split_shuffle, i, cards), x) import matplotlib.pyplot as plt %matplotlib inline plt.figure(figsize=(12,8)) plt.plot(x, y, label = u'       3') plt.plot(x, [1./(cards-1)] * len(x), label = u' ') plt.grid() plt.legend() 

Em geral, podemos assumir que 60 iterações são a quantidade ideal, menos é definitivamente ruim. Eu faço cerca de 16 a 17 iterações em 30 segundos. Isso significa que, para uma reprodução normal , levará quase dois minutos .

Meus amigos e eu nunca misturamos muito as cartas. E isso significa que nosso jogo é muito influenciado pelo saldo do último jogo.

Tenha cuidado :)