Os métodos de Newton-Cotes são uma combinação de técnicas aproximadas de integração baseadas em:
- dividir o intervalo de integração em intervalos iguais;
- aproximações do integrando em intervalos selecionados por polinômios;
- encontrar a área total do trapézio curvo obtido.
Este artigo abordará vários métodos de Newton-Cotes:
- método trapezoidal;
- Método de Simpson;
- Método de Romberg.
Método trapézio
O método trapézio é o mais simples dos considerados. Como exemplo, considere a seguinte integral:
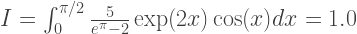
A precisão da aproximação depende do número N de segmentos nos quais o intervalo de integração é dividido. Assim, o comprimento do espaço:
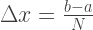
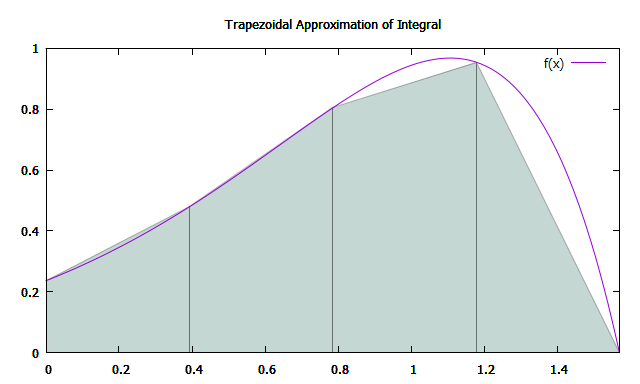
A área do trapézio pode ser calculada pela fórmula:
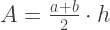
Resumindo todas as opções acima, o valor aproximado da integral é calculado pela fórmula:
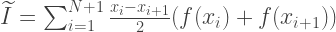
A função que calcula a integral pelo método trapézio deve ter 4 parâmetros:
- limites do segmento de integração;
- função integrando;
- o número N de intervalos da partição.
double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double trapezoidal_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2)); } return trapezoidal_integral; }
Método Simpson
O método Simpson consiste em integrar o polinômio de interpolação de segundo grau da função f (x) com os nós de interpolação a, bec = = (a + b) / 2 - parábolas p (x). Para aumentar a precisão, faz sentido dividir o segmento de integração em N intervalos iguais ( por analogia com o método trapézio), em cada um dos quais se aplica o método Simpson.
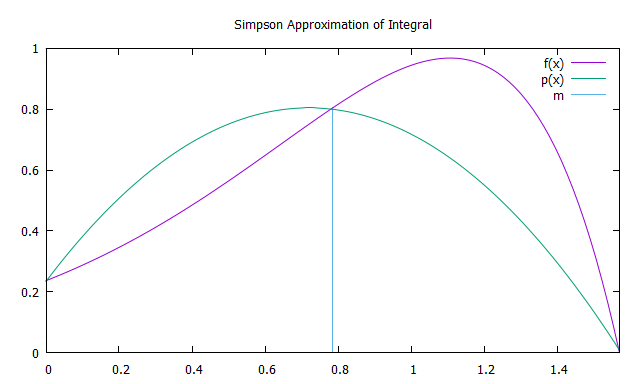
A área da parábola pode ser encontrada somando as áreas de 6 retângulos de igual largura. A altura do primeiro deles deve ser igual a f (a), do terceiro ao quinto - f (m), o sexto - f (m). Assim, a aproximação pelo método Simpson é encontrada pela fórmula:
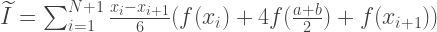
double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double simpson_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2)); } return simpson_integral; }
Método Romberg
Seja T (x) a aproximação integral obtida pelo método trapezoidal com o passo x. Temos três aproximações, reduzindo o tamanho do passo em 2 vezes com cada cálculo.

Agora construímos uma parábola simétrica em relação ao eixo y, passando pelos pontos T (1) e T (1/2) para extrapolar os valores obtidos para x tendendo a 0.
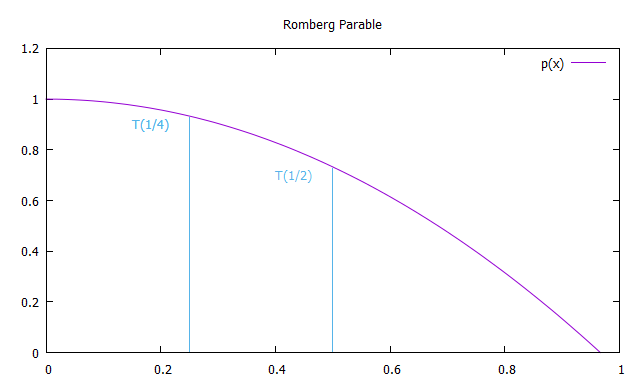
Portanto, cada membro da primeira coluna R (n, 0) das aproximações de Romberg é equivalente às soluções obtidas pelo método trapezóide, e cada solução da segunda coluna de R (n, 1) é equivalente ao método Simpson. Assim, as fórmulas para integração aproximada pelo método Romberg:
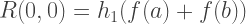
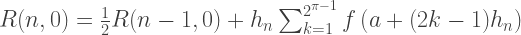
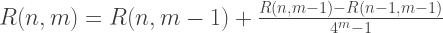
Implementação em C ++:
std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) { std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n)); romberg_integral.front().front() = trapezoidalIntegral(a, b, 1, f); double h = ba; for(size_t step = 1; step < n; step++) { h *= 0.5; double trapezoidal_integration = 0; size_t stepEnd = pow(2, step - 1); for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) { const double deltaX = (2*tzStep - 1)*h; trapezoidal_integration += f(a + deltaX); } romberg_integral[step].front() = 0.5*romberg_integral[step - 1].front() + trapezoidal_integration*h; for(size_t rbStep = 1; rbStep <= step; rbStep++) { const double k = pow(4, rbStep); romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1); } } return romberg_integral; }