A cor da lua e do sol do espaço em termos de RGB e temperatura de cor

Parece que a questão da cor da lua e do sol no espaço para a ciência moderna é tão simples que, em nosso século, não deveria haver nenhum problema com a resposta. Estamos falando de cores ao observar precisamente do espaço, pois a atmosfera causa uma mudança de cor devido à dispersão da luz Rayleigh. "Certamente em algum lugar da enciclopédia sobre isso em detalhes, em números há muito que foi escrito", você dirá. Bem, agora tente pesquisar na Internet para obter informações sobre isso. Aconteceu? Provavelmente não. O máximo que você encontrará é algumas palavras sobre o fato de a Lua ter um tom acastanhado e o Sol estar avermelhado. Mas você não encontrará informações sobre se essas tonalidades são visíveis ao olho humano ou não, especialmente o significado das cores em RGB ou pelo menos a temperatura das cores. Mas você encontrará várias fotos e vídeos em que a Lua do espaço é absolutamente cinza, principalmente nas fotos do programa americano Apollo, e onde o Sol do espaço é retratado em branco e até azul.

Especialmente minha opinião pessoal nada mais é do que uma consequência da intervenção da política na ciência. Afinal, as cores da Lua e do Sol do espaço estão diretamente relacionadas aos vôos dos americanos à Lua.

Pesquisei muitos artigos e livros científicos em busca de informações sobre a cor da lua e do sol do espaço. Felizmente, apesar de não terem uma resposta direta ao RGB, há informações completas sobre a densidade espectral da radiação solar e a refletividade da Lua em todo o espectro. Isso é suficiente para obter cores precisas nos valores RGB. Você só precisa calcular cuidadosamente o que, de fato, eu fiz. Neste artigo, compartilharei os resultados dos cálculos com você e, é claro, explicarei em detalhes sobre os próprios cálculos. E você verá a lua e o sol do espaço em cores reais!

Realizei os cálculos no programa Mathcad e, consequentemente, os fragmentos de código estarão na linguagem de programação interna, o que é bastante adequado e compreensível para todos os pseudo-códigos.

Ao mesmo tempo, explicarei em detalhes qual é o modelo de cores RGB, com o qual, creio, todos estão familiarizados. Esta questão também não é totalmente simples. Por exemplo, tente responder às duas perguntas a seguir. Deixe a cor ser definida como rgb (120,80,100) .
1) Quais valores de RGB possuem uma cor 2 vezes mais escura que a especificada?
2) Quais são os valores de RGB em cinza com o mesmo brilho que o especificado?
Parece que existe pensamento, dividido por 2 no primeiro caso, ou seja, rgb (60,40,50) e, em média, no segundo caso, ou seja, rgb (100,100,100) . Infelizmente, as respostas corretas são: 1) rgb (86.56.71) ; 2) rgb (92.92.92) . Você descobrirá por que as respostas são exatamente assim.

Fale também sobre a temperatura da cor e como calculá-la.

Espaço de cores XYZ

XYZ é um modelo mestre de cores, definido em estrito sentido matemático pela Organização Internacional de Iluminação da CIE (Comissão Internacional de Iluminação) em 1931. O modelo CIE XYZ é um modelo mestre de quase todos os outros modelos de cores usados ​​em áreas técnicas. A cor XYZ é definida da seguinte forma:

$$

$$X = \ int _ {390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {x}} (\ lambda) \, d \ lambda \\ Y = \ int _ { 390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda \\ Z = \ int _ {390 \, nm} ^ { 830 \, nm} I (\ lambda) \, {\ overline {z}} (\ lambda) \, d \ lambda$$

onde $$$I (\ lambda)$ - a densidade espectral de qualquer valor fotométrico de energia (por exemplo, fluxo de radiação, brilho de energia, etc., em termos absolutos ou relativos) na faixa de comprimento de onda de 390 a 830 nm (isto é, de acordo com 2006, em 1931, a faixa era de 380 a 780 nm ); $$${\ overline {x}} (\ lambda)$ , $$${\ overline {y}} (\ lambda)$ , $$${\ overline {z}} (\ lambda)$ - funções de correspondência de cores. Além disso, o que é importante para nós, a coordenada Y corresponde ao brilho visual do sinal.

Eu baixei essas funções de correspondência de cores aqui: [ 1 ]. Lá, as funções de correspondência de cores são definidas para um campo de visão de 2 e 10 graus . Decidi realizar cálculos para os dois casos, comparar os resultados e garantir que, como seria de esperar, as coordenadas das cores sejam ligeiramente diferentes. Naturalmente, usei os dados das funções com a resolução máxima das fornecidas, ou seja, com uma etapa de 0,1 nm . Os gráficos das funções de correspondência de cores são os seguintes:



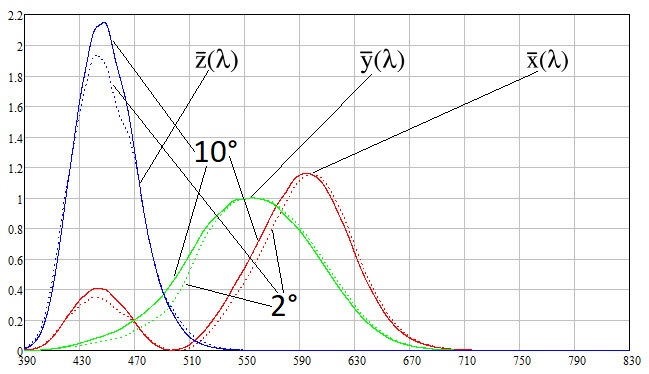
A partir dos gráficos, pode ser observado que acima de 710 nm , as funções se tornam desprezíveis no sentido de que, ao observar cores próximas ao branco, a densidade espectral na faixa acima de 710 nm quase não contribui. Embora saibamos que a luz visível está na faixa de até 780 nm , devemos entender que isso ocorre com radiação monocromática. Tenho tudo isso no fato de que, em cálculos, tive que extrapolar em alguns casos os dados ausentes sobre a refletividade da Lua apenas para o intervalo em que as funções de correspondência de cores são essencialmente pequenas. Portanto, um possível erro de extrapolação não leva a um erro perceptível nas cores calculadas.

Calculo as integrais acima pela regra trapezoidal :


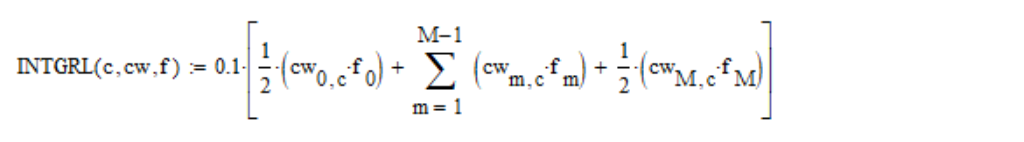
onde c - é o número de coordenadas do espaço de cores (1, 2, 3 para X, Y, Z, respectivamente); cw - é uma tabela de funções de correspondência de cores; f - é a densidade espectral; M = (830-390) /0.1=4400 - o número de etapas da grade.

As funções de correspondência de cores corretas têm a propriedade de que a área nas três curvas é a mesma:

$$

$$\ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {x}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {y}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {z}} (\ lambda) \, d \ lambda$$

Isso é feito para que o espectro uniforme tenha os mesmos valores de coordenadas XYZ. Verifique se esta propriedade possui:


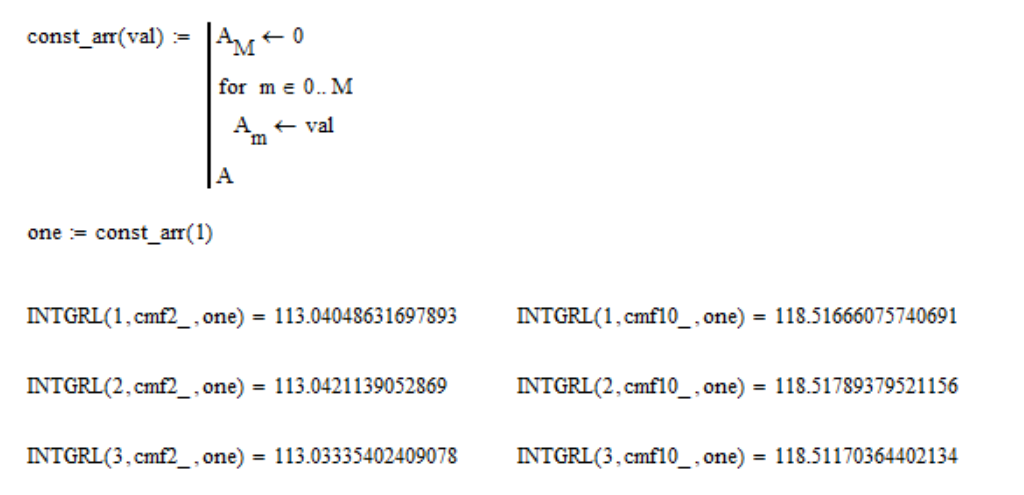
onde "um" - é uma matriz de 1; cmf2_ e cmf10_ - são tabelas de funções de correspondência de cores para o campo de visão de 2 e 10 graus , respectivamente. Como você pode ver, a propriedade é executada com aproximadamente 0,01% de precisão, o que é bastante bom. Mas ainda assim, renormalize as funções de fidelidade:

Normalização de brilho

Considere o trabalho de uma câmera digital. O principal elemento de uma câmera digital é uma matriz, que consiste em fotosensores. Quando uma imagem é projetada em uma matriz, uma carga elétrica é acumulada em cada um de seus fotossensores, o que é proporcional à energia de radiação do fotossensor. Os fotossensores capturam o brilho do elemento da imagem, sem transportar nenhuma informação sobre sua cor. Para obter informações sobre a cor, a matriz de fotossensores é coberta por filtros em miniatura. Esses filtros desempenham o papel das funções de correspondência de cores. Cada pixel consiste em vários fotosensores, que são combinados na quantidade de vários filtros de luz.

Assim, como uma função $$$I (\ lambda)$ devemos tomar a densidade espectral da energia de radiação de um pixel. Essa densidade espectral pode ser representada como

$$

$$I (\ lambda) = iluminação do coef \ cdot (\ lambda) \ cdot albedo (\ lambda)$$

onde iluminação - é a densidade espectral da fonte de luz; albedo - a refletividade da superfície do objeto fotografado; coef - é um certo coeficiente constante, que é determinado pelo tempo de exposição, abertura, distância da fonte de luz ao objeto sendo fotografado e outros fatores. Refletância refere-se ao albedo visível , que é definido como a razão entre o brilho de um elemento de superfície plana iluminado por um feixe paralelo de raios e o brilho da superfície absolutamente branca localizada perpendicular aos raios.

Agora imagine que estamos fazendo o trabalho do medidor de fotoexposição, com o qual o fotógrafo define a velocidade do obturador e a abertura da câmera. Em outras palavras, precisamos escolher um valor de coef para que a imagem fique com brilho normal, nem muito escuro, nem muito claro. Imagine que existe a tela absolutamente branca atrás do objeto que está sendo fotografado. A refletividade albedo de tal tela é por definição igual a 1 em todos os comprimentos de onda. Defina o valor do coef de forma que o brilho visual Y dessa tela seja igual a 1. Por que 1? Como no modelo de cores RGB, o valor máximo possível de brilho é 1, o que é alcançado com rgb (255.255.255) , ou seja, com branco. Vou contar um pouco mais tarde. Como os corpos normais têm cores mais escuras do que a tela absolutamente branca, as imagens ficarão com brilho normal. A partir dessas considerações, obtemos a seguinte expressão para coef :

$$

$$coef = \ frac {1} {\ int _ {390 \, nm} ^ {830 \, nm} iluminação (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda}$$

Observe que essa normalização não garante que o valor de cada coordenada RGB seja menor ou igual a 255. Por exemplo, se você fotografar a tela absolutamente branca com uma fonte de luz vermelha, a cor RGB será apagada a balança.

Portanto, calculo os valores das coordenadas do espaço de cores XYZ da seguinte maneira:


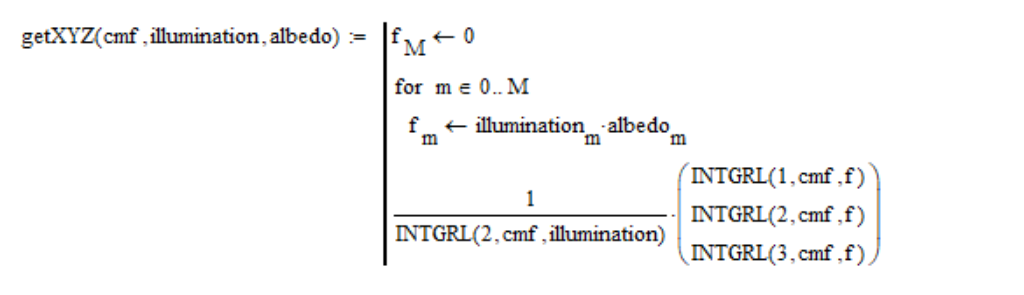
Precisamos de alguma forma expressar a cor do sol. Não podemos fotografá-lo diretamente e, em nosso modelo matemático, não previmos um caso tão extremo. Obviamente, precisamos fotografar a superfície absolutamente branca iluminada pelo sol. Como o Sol do espaço tem uma tonalidade avermelhada, então, como eu disse, a cor da tela absolutamente branca desaparece da escala. Portanto, devemos tomar a superfície mais escura. Eu descobri empiricamente que devemos levar um papel branco com um albedo de 0,91. Mais albedo não pode ser tomado, começa a sair da balança. Portanto, para obter a cor do Sol, basta definir o valor de albedo como 0,91 em todos os comprimentos de onda na fórmula acima:

espaço de cores sRGB

O espaço de cores mais comum usando o modelo RGB é sRGB. Portanto, quando eles falam sobre RGB sem esclarecimentos, é o espaço de cores sRGB que é o padrão para representar o espectro de cores usando o modelo RGB. Esse padrão foi criado pelo International Color Consortium (ICC) em 1996 para unificar o uso do modelo RGB em monitores, impressoras e sites da Internet. Vamos analisar esse padrão, cuja descrição está disponível em [ 2 ].

A conversão de XYZ em sRGB ocorre em três estágios. Primeiro, as coordenadas XYZ são convertidas em coordenadas lineares RGB, depois as coordenadas lineares são convertidas em coordenadas RGB não lineares e, no final, as coordenadas não lineares são convertidas em coordenadas RGB de 8 bits, que de fato são as coordenadas do espaço de cores sRGB.

A conversão de coordenadas XYZ em coordenadas lineares RGB é a seguinte:



e o oposto é:



Eu me pergunto de onde vieram esses números estranhos em matrizes quadradas? E eles vieram da recomendação da ITU-R BT.709 [ 3 ]. Denote a primeira matriz quadrada por XYZ_to_RGB e a segunda por RGB_to_XYZ . Obviamente, eles são mutuamente inversos. A recomendação ITU-R BT.709 especifica os requisitos para a segunda matriz. A partir desses requisitos, é possível calcular exclusivamente a segunda matriz e a primeira é igual à matriz inversa da segunda.

Apresentamos as seguintes funções:

$$

$$XYZ (R, G, B) = RGB \ _para _XYZ \ cdot {\ begin {bmatrix} R \\ G \\ B \ end {bmatrix}} \\ W (R, G, B) = XYZ_1 (R , G, B) + XYZ_2 (R, G, B) + XYZ_3 (R, G, B) \\ xy (R, G, B) = \ frac {1} {W (R, G, B)} \ cdot {\ begin {bmatrix} XYZ_1 (R, G, B) \\ XYZ_2 (R, G, B) \ end {bmatrix}}$$

Em seguida, os requisitos das recomendações ITU-R BT.709 assumem a seguinte forma:

$$

$$xy (1,0,0) = {\ begin {bmatrix} 0,64 \\ 0,33 \ end {bmatrix}}, \; xy (0,1,0) = {\ begin {bmatrix} 0,30 \\ 0,60 \ end {bmatrix}}, \; xy (0,0,1) = {\ begin {bmatrix} 0,15 \\ 0,06 \ end {bmatrix}} \\ xy (1,1,1) = {\ begin {bmatrix} 0,3127 \\ 0,3290 \ end {bmatrix }}$$

Temos 8 equações, quando temos 9 elementos desconhecidos da matriz RGB_to_XYZ , ou seja, falta mais uma equação. E a equação em falta é dada implicitamente, eu tive que adivinhar antes. A essência dessa equação é que, para a cor branca, o brilho visual Y deve ser igual a 1:

$$

$$XYZ_2 (1,1,1) = 1$$

Encontrei a solução exata dessas equações em números racionais:


Se você arredondar os números no meu resultado para quatro casas decimais após o ponto, você obterá esses números estranhos no padrão do International Color Consortium. Nos meus cálculos, não uso matrizes arredondadas, mas as exatas mencionadas acima (na medida em que os números de ponto flutuante com dupla precisão permitem).

Assim, as coordenadas lineares do RGB com base na tabela de funções de correspondência de cores (cmf), densidade de radiação espectral (iluminação) e refletividade (albedo) são calculadas da seguinte forma:



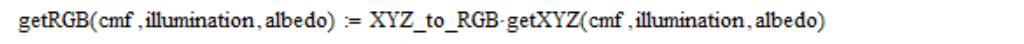
Eu também uso coordenadas lineares RGB, com média sobre o campo de visão de 2 e 10 graus :



A partir das coordenadas lineares do RGB, o brilho visual Y é calculado usando a seguinte fórmula (por padrão, as matrizes do Mathcad são numeradas a partir do elemento zero):


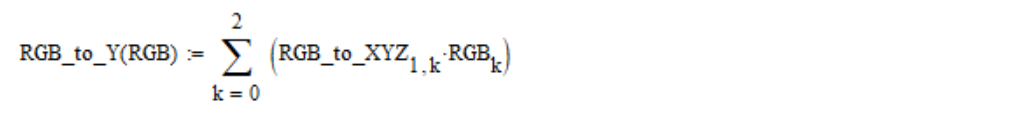
Continuamos a desmontar o padrão. Cada coordenada linear do RGB é convertida em não linear usando a função não linear lin2bit e retornando ao bit2lin, que são definidos da seguinte forma:


Os gráficos dessas funções são assim:



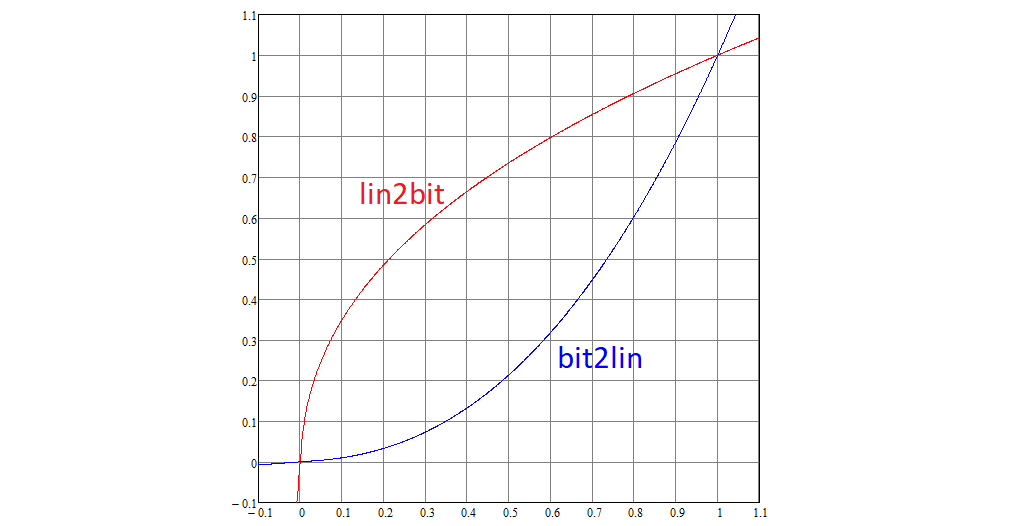
Observe que 0 é convertido em 0, 1 em 1.

No final, as coordenadas não lineares do RGB são convertidas em 8 bits multiplicando por 255, seguidas pelo arredondamento para números inteiros.

Assim, defini as seguintes funções para converter coordenadas lineares RGB em 8 bits e vice-versa:

Agora estamos prontos para resolver o problema desde a introdução. Lembro a condição.

Deixe a cor ser definida como rgb (120,80,100) .
1) Quais são os valores de RGB com uma cor 2 vezes mais escura que a especificada?
2) Quais são os valores RGB para cinza com o mesmo brilho que o fornecido?

Solução:

Respostas: 1) rgb (86.56.71) ; 2) rgb (92.92.92) .

Temperatura de cor

A temperatura da cor da fonte de luz, medida em Kelvin, é determinada pela temperatura do corpo negro localizado na tabela de cores no mesmo local da fonte de radiação em consideração. Se a fonte de luz não cair na curva de Planck (uma curva que é determinada pelo conjunto de pontos de cor de um corpo negro a diferentes temperaturas), uma temperatura de cor correlacionada é usada para caracterizá-la. Esse valor também é medido em Kelvin e é determinado pela temperatura de um corpo negro, cuja cor é o mais próxima possível da cor da fonte de luz. Para encontrar a temperatura de cor correlacionada da fonte de radiação na tabela de cores construída nas coordenadas (u, v) , é determinado o ponto mais próximo da fonte na curva de Planck (ou seja, a menor distância geométrica). A temperatura de um corpo negro localizado neste ponto corresponderá à temperatura de cor correlacionada da fonte em consideração [ 4 ].

Para um corpo negro de temperatura T, a potência de radiação por unidade de área da superfície radiante em um intervalo de comprimento de onda unitário é expressa pela lei de Planck :

$$

$$R (\ lambda, T) = \ frac {2 \ pi h c ^ 2} {\ lambda ^ 5} \ frac {1} {e ^ {h c / \ lambda k T} -1}$$

Portanto, calculo a densidade espectral da radiação do corpo negro da seguinte forma (na coluna zero da tabela de funções de correspondência de cores cmf2 estão os valores do comprimento de onda em nanômetros):



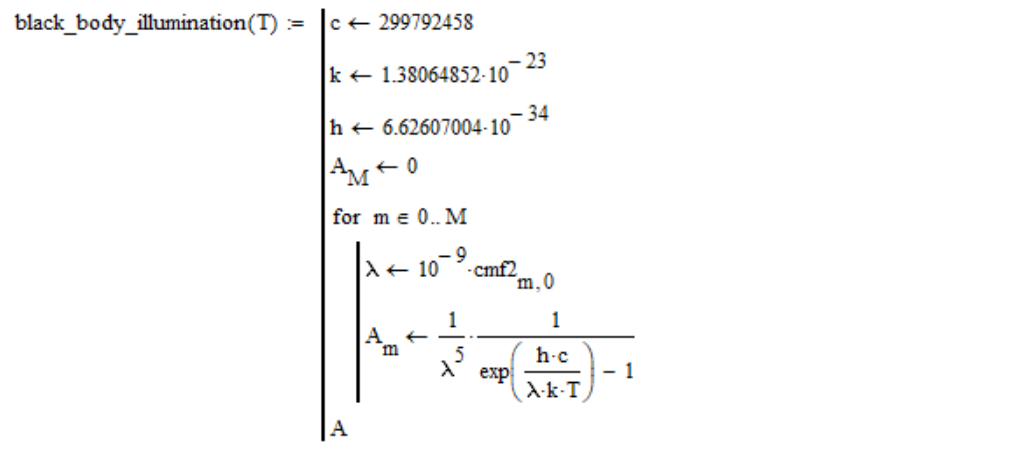
Observe que pulei o fator constante, pois ele ainda é reduzido com mais normalização no brilho (o brilho da fonte de luz não afeta a temperatura da cor).

Então eu calculo as coordenadas lineares do RGB:



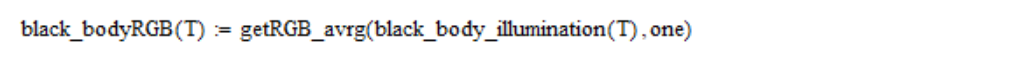
As coordenadas lineares RGB são convertidas em coordenadas (u, v) da seguinte maneira:



No plano (u, v) , calcula-se a distância geométrica entre os pontos da cor considerada e a cor de um corpo negro de uma determinada temperatura T:



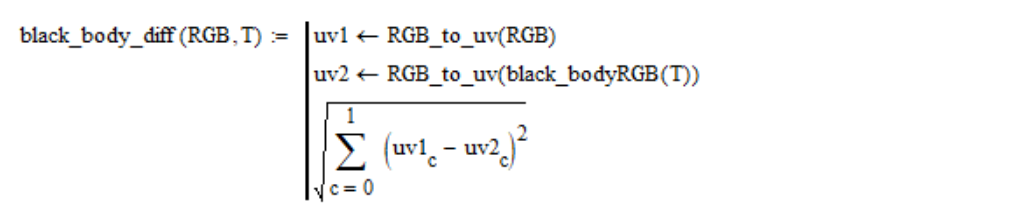
Por exemplo, para a fonte de luz branca padrão, a dependência dessa distância da temperatura é assim:



O valor de T no qual essa dependência tem um mínimo é a temperatura da cor da fonte de luz considerada.

Densidade espectral da radiação do sol

Os dados da densidade espectral da radiação solar na ausência da atmosfera foram baixados aqui: [ 5 ]. A fonte de luz correspondente ao Sol do espaço, chamarei de E490 no futuro. Também para comparação nos cálculos, considero o iluminante padrão D65 . Esta fonte representa luz branca. Olho para mostrar como seria a Lua se o Sol fosse branco. Os dados da densidade espectral de radiação do iluminante padrão D65 foram baixados aqui: [ 6 ].

Como será mostrado abaixo, as fontes de luz D65 e E490 têm temperaturas de cor de 6467K e 5912K, respectivamente. As densidades de radiação espectral das fontes de luz D65, E490 e corpos absolutamente negros das temperaturas correspondentes são as seguintes:



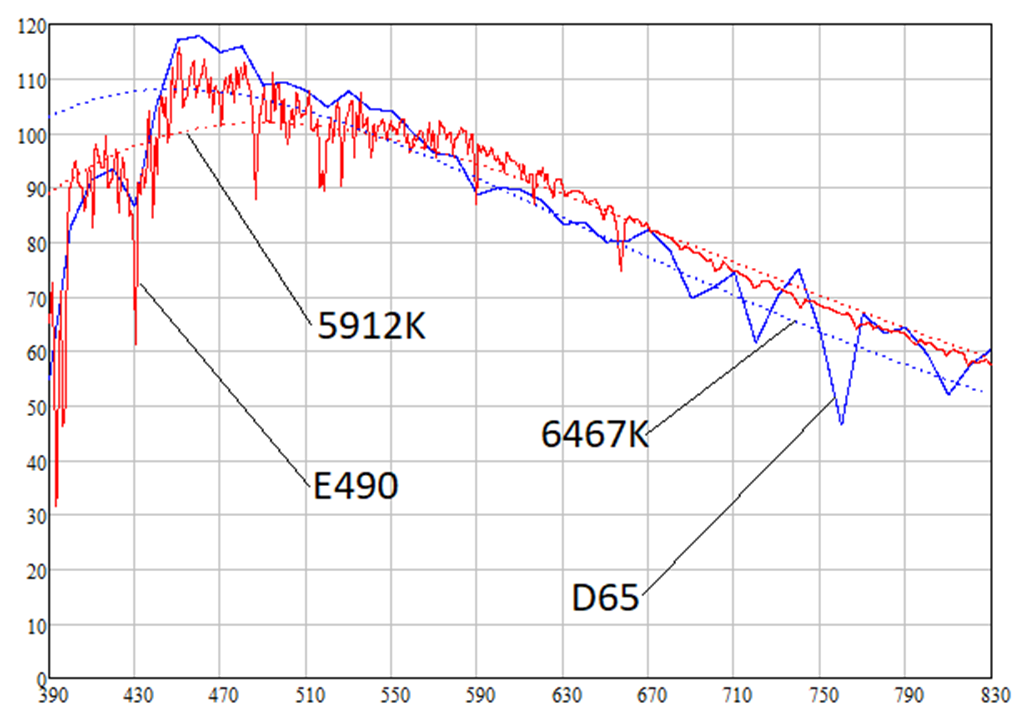
Você pode ver que a densidade espectral da radiação solar é maior que a de uma fonte de luz branca em comprimentos de onda mais longos, ou seja, em comprimentos de onda da luz vermelha (620-770 nm). Isso significa que o Sol tem um tom avermelhado. De fato, os cálculos dão as seguintes cores das fontes de luz D65, E490 e corpos negros de temperaturas correspondentes (como eu disse, é considerado papel branco com um albedo de 0,91):



Observe que as coordenadas do sRGB do Sol e uma temperatura do corpo negro de 5912K correspondem exatamente. Isso não é explicado por nada, apenas acontece.

A cor dos círculos na última foto é a verdadeira cor do Sol do espaço. O olho humano vê claramente o tom avermelhado do sol. Então, o fato de o Sol do espaço ser branco é um grande mito! Deve-se notar que, por algum motivo, esse tom não é observado nas fotos e vídeos da Apollo. Em fotografias reais, o tom avermelhado visível do Sol certamente apareceria nas superfícies brancas da bandeira e dos trajes espaciais americanos. E, como será mostrado abaixo, esse tom do Sol contribui significativamente para a "vermelhidão" da Lua a partir do espaço.

A Lua é diferente ou da mesma cor?

Opositores da teoria da conspiração lunar promovem a versão de que a Lua tem uma cor diferente. Alegadamente, a Lua é cinza em alguns lugares, marrom em alguns lugares, e os Apollos pousaram onde a Lua é cinza. Mas esta versão contradiz diretamente os dados científicos. O artigo [ 7 ] afirma claramente:

As diferenças de cores na Lua são extremamente pequenas.

Shevchenko também escreve em seu livro [ 8 ]:

Por muitos anos, o famoso pesquisador americano T. McCord trabalhou nessa direção. Ele obteve mais de 200 espectros para diferentes partes da superfície lunar de 10 a 20 km cada. Todas as curvas obtidas são basicamente de aparência semelhante.

Então, não, a Lua não é diferente em cores, mas é a mesma.

Dados de cores de acordo com Shevchenko

Shevchenko em seu livro [ 8 ] fornece a seguinte dependência da refletividade no comprimento de onda.



Nos meus cálculos, aplico a interpolação linear por partes desses dados. Os dados ausentes no intervalo de 820-830 nm, recebi por continuação direta do segmento no intervalo de 690-820 nm.

Dados de cores de acordo com a LRO

A dependência da refletividade da superfície lunar nas condições de iluminação e observação em comprimentos de onda de 321 nm a 689 nm é dada em [ 9 ]. Os parâmetros do modelo foram calculados com base na análise dos dados obtidos pelo Lunar Reconnaissance Orbiter (LRO). As condições de iluminação e observação são determinadas pelos três parâmetros i (ângulo de incidência), e (ângulo de reflexão) e g (ângulo de fase). Esses ângulos são mostrados no diagrama a seguir:



O ângulo de fase pode ser expresso em termos do ângulo de azimute $$$\ varPsi$ usando a lei esférica dos cossenos da seguinte maneira:

$$

$$g = \ arccos \ esquerda (\ cos \ esquerda (i \ direita) \ cos \ esquerda (e \ direita) + \ sin \ esquerda (i \ direita) \ sin \ esquerda (e \ direita) \ cos \ esquerda ( \ varPsi \ right) \ right)$$

Nos cálculos, tomo os valores tradicionais dos ângulos i = g = 30 °, e = 0 °. Para tais ângulos, é obtida a seguinte dependência da refletividade no comprimento de onda (gráfico lro30):


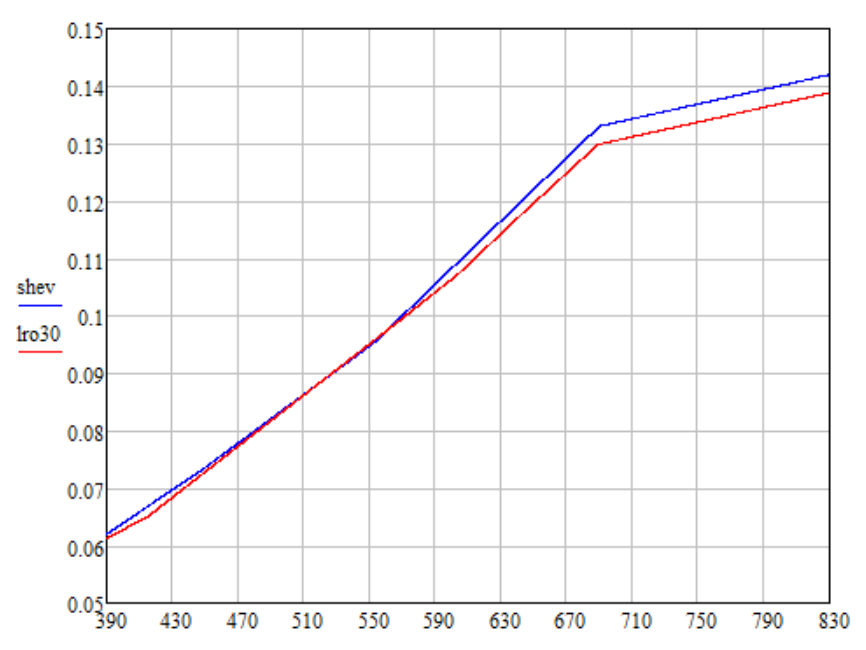
Fiz uma extrapolação linear dos dados da LRO no intervalo de 689-830 nm, de modo que a razão dos valores nos pontos de 830 nm e 689 nm fosse a mesma que a dos dados de Shevchenko (gráfico de shev). Também renormalizei os dados de Shevchenko multiplicando por 0,8315 para que o brilho da cor resultante de acordo com Shevchenko e LRO fosse o mesmo.

Dados de cores de acordo com "Kaguya"

Em [ 10 ], são apresentados dados obtidos pelo segundo satélite artificial japonês da Lua. Infelizmente, a refletividade na faixa do comprimento de onda visível é fornecida com uma resolução muito baixa, portanto, não a uso nos meus cálculos.

Mas o trabalho é interessante, pois fala das discrepâncias colossais entre os dados de Kaguya e os da missão Apollo 16. E este é um dos raros casos em que a comunidade científica fala abertamente de inconsistências associadas aos voos dos americanos para a Lua.

Resultados do cálculo

Além disso, usarei a seguinte notação:
D65 - fonte de luz branca padrão D65;
E490 - a fonte de luz do Sol na ausência da atmosfera;
W-0,91 - papel branco com albedo 0,91;
LRO (30 °) - dados de LRO para ângulos tradicionais i = g = 30 °, e = 0 °;
Shevch. - dados de Shevchenko;
lin. (2 °) - coordenadas lineares de RGB com campo de visão de 2 graus ;
lin. (10 °) - coordenadas lineares de RGB com campo de visão de 10 graus ;
lin. (média) - coordenadas lineares RGB, com média sobre o campo de visão de 2 e 10 graus ;
sRGB (100%) - coordenadas de sRGB, obtidas a partir de coordenadas lineares RGB, em média no campo de visão de 2 e 10 graus ;
sRGB (200%) - coordenadas de sRGB, obtidas a partir das coordenadas lineares duplicadas de RGB, em média no campo de visão de 2 e 10 graus ;
sRGB (300%) - coordenadas de sRGB, obtidas a partir das coordenadas lineares triplas de RGB, com média no campo de visão de 2 e 10 graus ;
sRGB (400%) - coordenadas de sRGB, obtidas a partir das coordenadas lineares quádruplas de RGB, em média no campo de visão de 2 e 10 graus ;
cl. temp. - temperatura da cor obtida a partir das coordenadas lineares do RGB, calculada a média sobre o campo de visão de 2 e 10 graus ;

D65

	W-0.91	LRO (30 °)	Shevch.
lin. (2 °)	0.9076,0.9120,0.8968	0.1177,0.0931,0.0688	0.1202,0.0931,0.0697
lin. (10 °)	0.9084,0.9122,0.8929	0.1165.0.0916.0.0687	0.1188,0.0917,0.0696
lin. (média)	0.9080,0.9121,0.8948	0.1171,0.0924,0.0688	0.1195,0.0924,0.0697
sRGB (100%)	rgb (244.245.243)	rgb (96.86.74)	rgb (97.86.75)
sRGB (200%)	-	rgb (133.119.104)	rgb (134.119.104)
sRGB (300%)	-	rgb (160.144.125)	rgb (161.144.126)
sRGB (400%)	-	rgb (182.164.143)	rgb (184.164.144)
cl. temp.	6467K	4928K	4891K

E490

	W-0.91	LRO (30 °)	Shevch.
lin. (2 °)	1.0005,0.8892,0.8490	0.1283.0.0909.0.0649	0.1310,0.0909,0.0657
lin. (10 °)	1.0021,0.8888,0.8483	0.1272.0.0895.0.0650	0.1297.0.0895.0.0659
lin. (média)	1.0013,0.8890,0.8486	0.1277,0.0902,0.0649	0.1303.0.0902.0.0658
sRGB (100%)	rgb (255.242.237)	rgb (100.85.72)	rgb (101.85.73)
sRGB (200%)	-	rgb (138.118.101)	rgb (140.118.102)
sRGB (300%)	-	rgb (166.142.122)	rgb (168.142.123)
sRGB (400%)	-	rgb (189.162.139)	rgb (191.162.140)
cl. temp.	5912K	4550K	4512K

A imagem a seguir mostra as cores de superfície da Lua sRGB (100%) , sRGB (200%) (brilho dobrado), sRGB (300%) (brilho triplo), sRGB (400%) (brilho quádruplo) com fonte de luz E490 (ou seja, quando observado a partir do espaço), de acordo com LRO e Shevchenko.



Como você pode ver, a Lua do espaço tem uma cor marrom, de acordo com os dados da LRO e com os dados de Shevchenko. Shevchenko acaba sendo um pouco (quase imperceptível) mais vermelho que o LRO.

Cor da lua nas fotos

Nesta seção, faremos a coloração das fotos. Deixe a imagem img e a cor nas coordenadas lineares RGB são fornecidas. Cada pixel da imagem é substituído por um pixel de uma determinada cor com o mesmo brilho que o pixel de origem. A imagem no programa Mathcad é representada como uma única matriz de coordenadas sRGB, obtida através da costura de três matrizes “R”, “G”, “B” da esquerda para a direita. Com isso em mente, o procedimento de coloração é o seguinte:

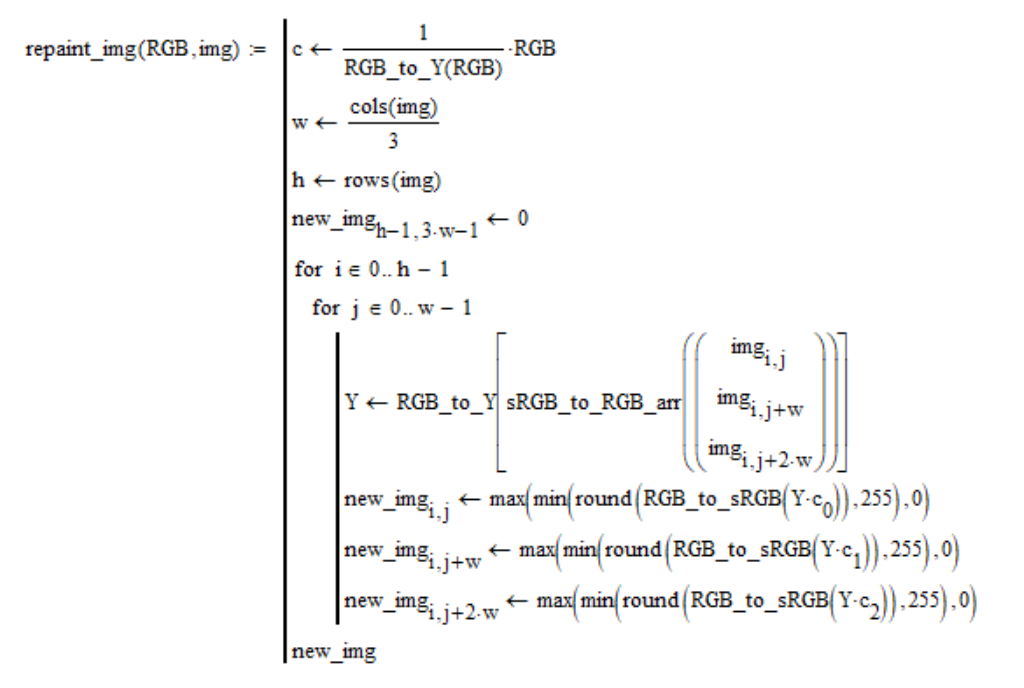
Por interesse, tirei fotografias do álbum de fotos da Apollo, representando a superfície lunar do programa americano, e repintei-o nas cores obtidas em meus cálculos. Eu dou apenas os resultados e a conclusão de que essas fotos autênticas ou falsas são suas.

O resultado da imagem AS11-44-6552 coloração:



No meio estão as fotos originais. À esquerda, as fotografias são pintadas em cores, de acordo com os dados da LRO nos ângulos tradicionais i = g = 30 °, e = 0 °, e à direita, de acordo com os dados de Shevchenko. A linha superior corresponde ao iluminante padrão D65, ou seja, a linha superior mostra as cores da superfície da Lua, que seriam obtidas se o Sol fosse branco. A linha inferior corresponde à fonte de luz E490, ou seja, a linha inferior mostra as cores naturais da superfície da Lua, vistas do espaço.

Como você pode ver, o tom avermelhado do Sol contribui significativamente para a "vermelhidão" da superfície da Lua, que no final parece marrom, e nem cinza.

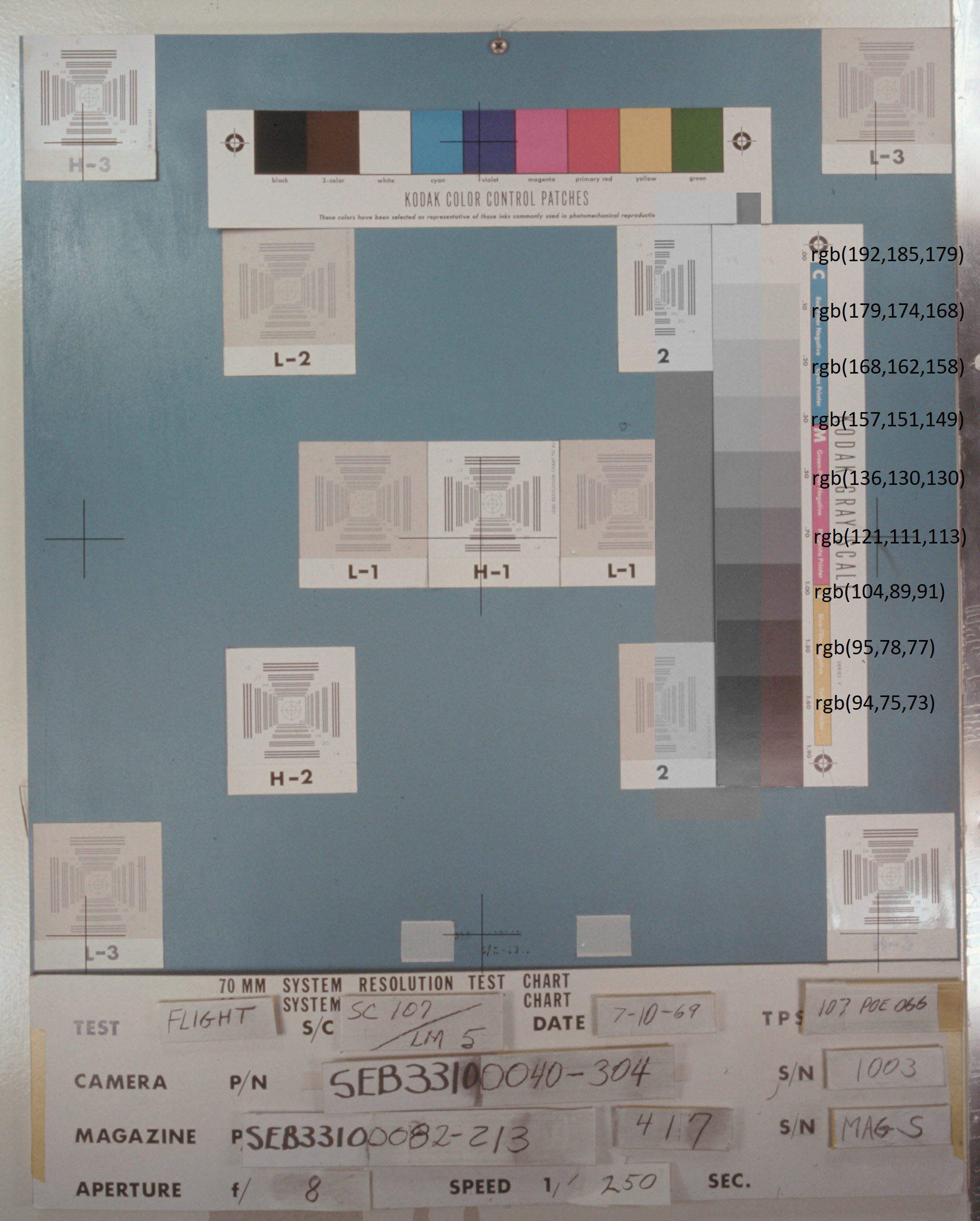
A cor cinza da Lua nas fotos da NASA pode ser explicada pelo fato de que, por algum motivo, o filme “foi embora” para azul, mas essa versão desaparece imediatamente se analisarmos as imagens de gradações de cinza no final dos álbuns. A fotografia no gráfico 11-44 mostra esse instantâneo para a última foto acima. Coloquei cinzas reais com o mesmo brilho da foto à esquerda das gradações de cinza e também escrevi os valores das coordenadas sRGB. O resultado foi a seguinte imagem:



Como você pode ver, o filme não apenas não "desapareceu" em azul, mas até um pouco "desapareceu" na direção oposta ao azul. Esse desvio não pode ficar marrom a cinza.

O resultado da foto para colorir AS11-40-5903 :



Na foto original, a superfície lunar em alguns lugares não tem apenas uma cor cinza, mas até um leve tom azulado. A fotografia como gráfico 11-40 mostra a imagem correspondente das gradações de cinza:



O filme "foi embora" não para a cor "azul", mas para o "vermelho". E mesmo depois disso, por algum motivo, a superfície lunar na foto da NASA é cinza.

O resultado da foto para colorir AS11-37-5455 :



Esta é uma das raras fotos do programa "Apollo", onde a superfície lunar tem uma tonalidade marrom, embora não totalmente. Os oponentes da teoria da conspiração lunar gostam de mostrá-la, dizem eles, parecer marrons. Mas o truque apareceu aqui. Vamos analisar a foto como 11-37-chart , que mostra a imagem correspondente das gradações de cinza:



O filme simplesmente "saiu" em marrom. Essa é toda a razão para o tom marrom da superfície lunar nas fotografias da NASA.

A dependência da cor da superfície lunar das condições de iluminação e observação

Usando os dados da LRO apresentados em [ 9 ], investigamos como a cor da superfície da Lua varia de acordo com as condições de iluminação e observação. Considere a fonte de luz E490 (o Sol do espaço) e os diferentes valores dos ângulos i , e , $$$\ varPsi$ . A figura a seguir mostra o resultado, onde na linha superior há cores com um brilho triplo e na linha inferior há cores reduzidas para o mesmo brilho Y = 0,5 .



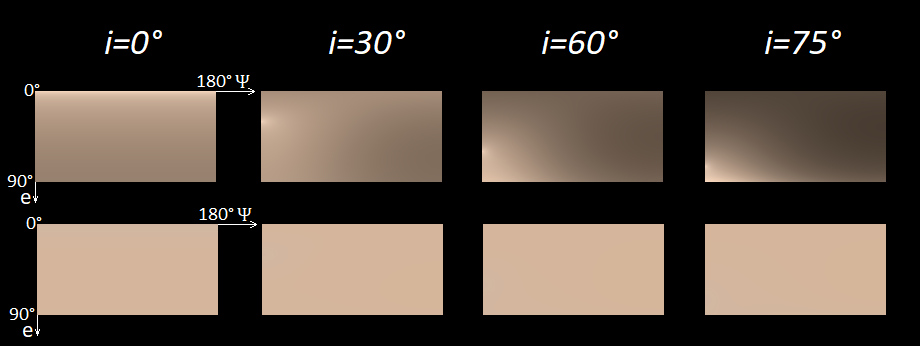
Como pode ser visto na imagem, apenas o brilho muda. Na linha inferior, as cores são quase as mesmas em todos os lugares para o olho humano. Embora, se você observar atentamente, no caso de i = 0 °, poderá ver um pequeno desvio na direção cinza quando e se aproxima de zero.

Cor do solo da lua

O site da NASA tem uma fotografia muito estranha, ou seja, esta fotografia da amostra de solo lunar nº 10005



O solo lunar na foto parece marrom, até marrom demais, dado que a iluminação foi produzida por uma fonte de luz branca. A correção do balanço de branco pode ser verificada pela cor do papel branco que entrou no quadro.

Talvez este seja o mesmo solo laranja que os astronautas da Apollo 17 encontraram? Não! O documento [ 11 ] afirma claramente que a amostra foi coletada pelos astronautas da Apollo 11.

E agora vamos ouvir o que Neil Armstrong (astronauta da Apollo 11) diz em uma entrevista com Patrick Moore [ 12 ] que ele deu em 1970.

Quando você olha o material de perto, como se estivesse em sua mão, na verdade, é um cinza-carvão, e nunca conseguimos encontrar coisas muito diferentes daquela cor.

Acontece que Neil Armstrong, sem medo da palavra, mentiu.

Literatura

1 Laboratório de Pesquisa em Cores e Visão - Novas funções CIE XYZ transformadas a partir das funções LMS CIE (2006)
2) International Color Consortium - um espaço de cores padrão padrão para a Internet: sRGB
3) Recomendação ITU-RBT.709 - Valores de parâmetro para os padrões HDTV para produção e intercâmbio internacional de programas
4) Robertson R. “Cálculo da temperatura de cor correlacionada e temperatura de distribuição” /.Opt. Soc. Am. 58, 1528 (1968).
5) 2000 Espectro extraterrestre padrão ASTM Referência E-490-00
6 Iluminante padrão CIE D65
7) "Os primeiros resultados da determinação das propriedades físico-mecânicas dos solos da Lua", M .: 1970. Gosstroy da URSS, ed. prof. Dr. Techn. Sciences VG Bulycheva, p. 8. ("Os Primeiros Resultados da Determinação das Propriedades Físico-Mecânicas dos Solos da Lua", Moscou: 1970. Gosstroy da URSS, sob a direção de redação do Prof. Dr. Sc. VG Bulychev, p. 8.)
8) Shevchenko VV, A Lua e sua observação, 1983, pp. 91-92. (Shevchenko V.V., Moon e sua observação, 1983, pp. 91-92.)
9 Hapke, B., B. Denevi, H. Sato, S. Braden e M. Robinson (2012), A dependência do comprimento de onda da curva da fase lunar, conforme visto pela Câmera de Grande Angular do Lunar Reconnaissance Orbiter, J. Geophys. Res., 117, E00H15
10) Ohtake, M. et al. (2010), Derivando a refletância absoluta da superfície lunar usando dados do gerador de imagens multibanda SELENE (Kaguya), Space Sci. Rev., 154, 57-77
11) THE APOLLO 11 DRIVE TUBES, Dissecção e descrição por Judith H. Allton, NASA (1978)
12) BBC Neil Armstrong fala com Patrick Moore (1970)