Como ensinar uma rede neural a reproduzir a física dos jogos

Em quase todos os jogos de computador modernos, a presença de um mecanismo físico é um pré-requisito. Bandeiras e coelhos tremulando ao vento, bombardeados por bolas - tudo isso requer execução adequada. E, é claro, mesmo que nem todos os heróis usem capas de chuva ... mas aqueles que usam realmente precisam de uma simulação adequada de tecido esvoaçante.



No entanto, a modelagem física completa dessas interações geralmente se torna impossível, pois é uma ordem de magnitude mais lenta que o necessário para jogos em tempo real. Este artigo oferece um novo método de modelagem que pode acelerar simulações físicas e torná-las 300-5000 vezes mais rápidas. Seu objetivo é tentar ensinar uma rede neural a simular forças físicas.

O progresso no desenvolvimento de motores físicos é determinado pelo crescente poder computacional dos equipamentos técnicos e pelo desenvolvimento de métodos de modelagem rápidos e estáveis. Tais métodos incluem, por exemplo, modelagem, cortando espaço em subespaços e abordagens orientadas a dados - ou seja, com base em dados. O primeiro funciona apenas em um subespaço reduzido ou compactado, onde apenas algumas formas de deformação são levadas em consideração. Para grandes projetos, isso pode levar a um aumento significativo nos requisitos técnicos. As abordagens orientadas a dados usam a memória do sistema e os dados pré-computados armazenados nele, o que reduz esses requisitos.

Aqui, examinamos uma abordagem que combina os dois métodos: dessa maneira, pretende-se capitalizar os pontos fortes de ambos. Esse método pode ser interpretado de duas maneiras: como um método de modelagem de subespaço parametrizado por uma rede neural ou como um método DD baseado na modelagem de subespaços para construir um meio simulado compactado.

Sua essência é a seguinte: primeiro coletamos dados de simulação de alta precisão usando o Maya nCloth e depois calculamos o subespaço linear usando o método do componente principal (PCA) . Na próxima etapa, usamos o aprendizado de máquina com base no modelo clássico de rede neural e em nossa nova metodologia, após o qual introduzimos o modelo treinado em um algoritmo interativo com várias otimizações, como um algoritmo de descompressão eficiente por uma GPU e um método para aproximar os vértices normais.


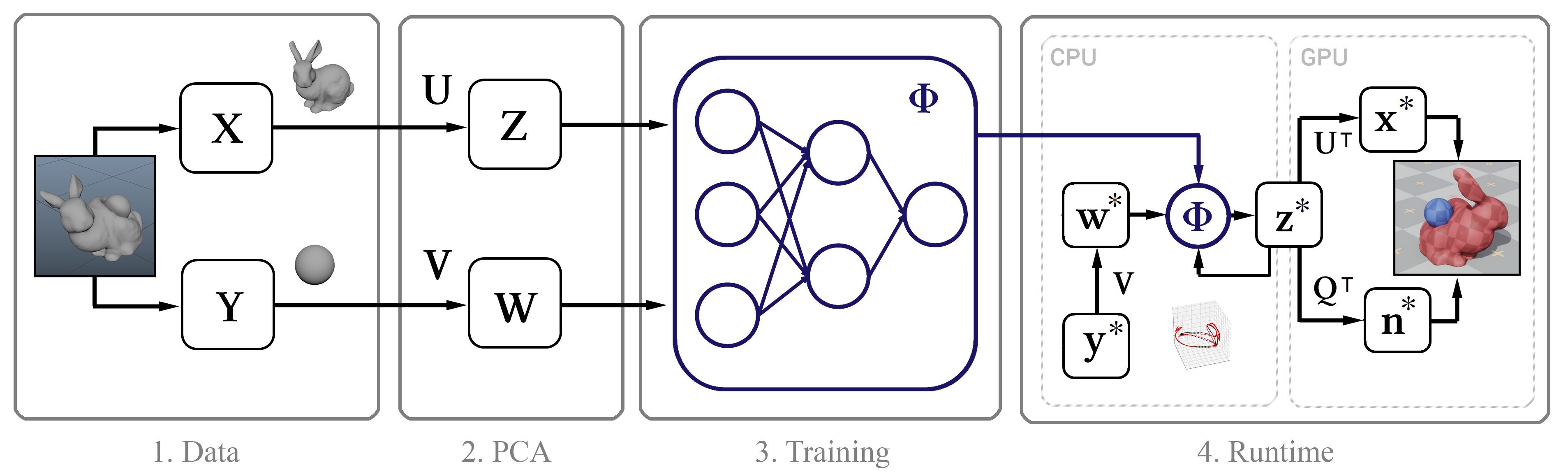Figura 1. O diagrama estrutural do método

Dados de treinamento

De um modo geral, a única entrada para esse método são os carimbos de data / hora brutos das posições quadro a quadro dos vértices do objeto. A seguir, descrevemos o processo de coleta desses dados.

Realizamos a simulação no Maya nCloth, capturando dados a uma velocidade de 60 quadros por segundo, com 5 ou 20 subetapas e 10 ou 25 iterações limitantes, dependendo da estabilidade da simulação. Para tecidos, use um modelo de camiseta com um leve aumento no peso do material e sua resistência ao esticamento e, para objetos deformáveis, borracha dura com atrito reduzido. Realizamos colisões externas colidindo triângulos de geometria externa, autocolisões - vértices com vértices para tecido e triângulos com triângulos para borracha. Em todos os casos, usamos uma espessura de colisão bastante grande - da ordem de 5 cm - para garantir a estabilidade do modelo e para evitar beliscar e rasgar o tecido.

Tabela 1. Parâmetros dos Objetos Modelados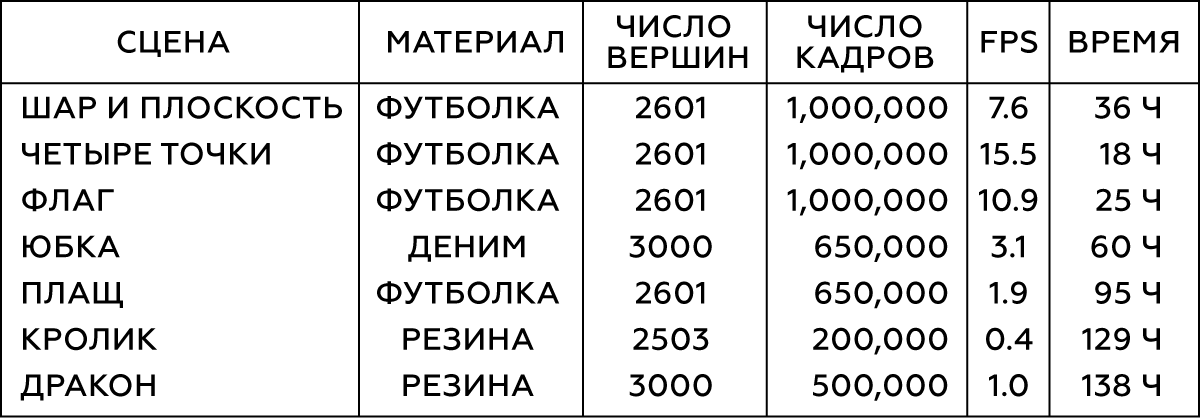


Para vários tipos de interação de objetos simples (por exemplo, esferas), geraremos seu movimento de maneira aleatória cortando coordenadas aleatórias em momentos aleatórios. Para simular a interação do tecido com um personagem, usamos um banco de dados de captura de movimento de 6,5 × 10 ⁵ quadros, que são uma grande animação. Após a conclusão da simulação, verificamos o resultado e excluímos os quadros com comportamento instável ou ruim. Para a cena com a saia, removemos as mãos do personagem, pois elas freqüentemente se cruzam com a geometria da malha das pernas e agora são insignificantes.


Figura 2. As duas primeiras cenas da tabela

Normalmente, precisamos de 10 ^{5 a} 10 ⁶ quadros de dados de treinamento. Em nossa experiência, na maioria dos casos, 10 ⁵ quadros é suficiente para teste, enquanto os melhores resultados são alcançados com 10 ⁶ quadros.

Treinamento

A seguir, falaremos sobre o processo de aprendizado de máquina: sobre parametrização em nossa rede neural, sobre arquitetura de rede e diretamente sobre a própria técnica.

Parametrização

Para obter um conjunto de dados de treinamento, coletamos as coordenadas dos vértices em cada quadro t em um vetor x _t e, em seguida, combinamos esses vetores quadro a quadro em uma grande matriz X. Essa matriz descreve os estados do objeto modelado. Além disso, devemos ter uma idéia do estado dos objetos externos em cada quadro. Para objetos simples (como bolas), é possível usar suas coordenadas tridimensionais, enquanto o estado de modelos complexos (personagem) é descrito pela posição de cada articulação em relação ao ponto de referência: no caso de uma saia, esse suporte será a articulação do quadril, no caso de uma capa - o pescoço. Para objetos com um sistema de referência móvel, a posição da Terra em relação a ele deve ser levada em consideração: então nosso sistema saberá a direção da gravidade, bem como sua velocidade linear, aceleração, velocidade de rotação e aceleração de rotação. Para a bandeira, levaremos em conta a velocidade e a direção do vento. Como resultado, para cada objeto, obtemos um vetor grande que descreve o estado do objeto externo, e todos esses vetores também são combinados na matriz Y.

Agora, aplicamos o PCA às matrizes X e Y e usamos as matrizes de transformação Z e W resultantes para construir a imagem do subespaço. Se o procedimento PCA exigir muita memória, primeiro experimente nossos dados.

A compactação do PCA inevitavelmente resulta em perda de detalhes, especialmente para objetos com muitas condições em potencial, como dobras finas de tecido. No entanto, se o subespaço consistir em 256 vetores base, isso geralmente ajudará a preservar a maioria dos detalhes. Abaixo estão animações da física padrão da capa e modelos com 256, 128 e 64 vetores base, respectivamente.


Figura 3. Comparação do modelo de controle (padrão) com os modelos obtidos por nosso método em espaços com diferentes bases de dimensão

Modelo de origem e estendido

Foi necessário desenvolver um modelo que pudesse prever o estado dos vetores de modelo em quadros futuros. E como os objetos modelados são geralmente caracterizados por inércia com tendência a um determinado estado médio de repouso (após o procedimento PCA, o objeto leva esse estado a valores zero), um bom modelo inicial seria a expressão representada pela linha 9 do algoritmo na Figura 4. Aqui α e β são os parâmetros do modelo, ⊙ é um produto explodido. Os valores desses parâmetros serão obtidos a partir dos dados de origem, resolvendo a equação linear dos mínimos quadrados individualmente para α e β:



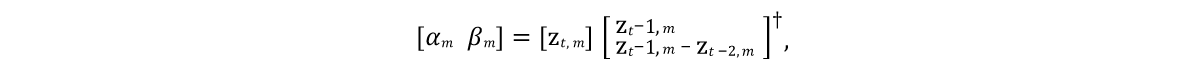
Aqui † é a transformação pseudo - inversa da matriz .

Como essa previsão é apenas uma aproximação muito aproximada e não leva em consideração a influência de objetos externos w, obviamente, não será possível modelar com precisão os dados de treinamento. Portanto, treinamos a rede neural Φ para aproximar os efeitos residuais do modelo de acordo com a 11ª linha do algoritmo. Aqui, parametrizamos uma rede neural de distribuição direta padrão com 10 camadas, para cada camada (exceto a saída), usando a função de ativação ReLU . Excluindo as camadas de entrada e saída, definimos o número de unidades ocultas em cada camada restante igual a um tamanho e meio dos dados do PCA, o que levou a um bom compromisso entre o espaço ocupado no disco rígido e o desempenho.


Figura 4. Algoritmo de aprendizado de rede neural

Treinamento em redes neurais

Uma maneira padrão de treinar uma rede neural seria iterar todo o conjunto de dados e treinar a rede para fazer previsões para cada quadro. Obviamente, essa abordagem levará a um baixo erro de aprendizado, mas o feedback dessa previsão causará um comportamento instável de seu resultado. Portanto, para garantir uma previsão estável a longo prazo, nosso algoritmo usa o método de propagação reversa de erros em todo o procedimento de integração.

Em geral, funciona assim: a partir de uma pequena janela de dados de treinamento z e w, pegamos os dois primeiros quadros z ₀ e z ₁ e adicionamos um pouco de ruído r ₀ , r _{1 a eles} , a fim de atrapalhar levemente o caminho de aprendizado. Então, para prever os próximos quadros, executamos o algoritmo várias vezes, retornando aos resultados anteriores das previsões a cada nova etapa de tempo. Assim que obtemos uma previsão de toda a trajetória, calculamos o erro médio de coordenadas e o passamos para o otimizador AmsGrad usando as derivadas automáticas calculadas usando o TensorFlow.

Repetiremos esse algoritmo em mini-amostras de 16 quadros, usando janelas sobrepostas de 32 quadros, por 100 épocas ou até o treinamento convergir. Utilizamos a taxa de aprendizado de 0,0001, o coeficiente de atenuação da taxa de aprendizado de 0,999 e o desvio padrão de ruído calculado a partir dos três primeiros componentes do espaço PCA. Esse treinamento leva de 10 a 48 horas, dependendo da complexidade da instalação e do tamanho dos dados do PCA.


Figura 5. Comparação visual da saia de referência e da que nossa rede neural aprendeu a construir

Implementação do sistema

Descreveremos em detalhes a implementação de nosso método em um ambiente interativo, incluindo a avaliação de uma rede neural, o cálculo das normais nas superfícies dos objetos para renderização e como lidamos com as interseções visíveis.

Aplicativo de renderização

Renderizamos os modelos resultantes em um aplicativo 3D interativo simples escrito em C ++ e DirectX: mais uma vez implementamos os pré-processos e operações de rede neural no código C ++ de thread único e carregamos os pesos de rede binários obtidos durante nosso procedimento de treinamento. Em seguida, aplicamos algumas otimizações simples para a estimativa da rede, em particular a reutilização de buffers de memória e dados esparsos da matriz vetorial, o que se torna possível devido à presença de zero unidades ocultas obtidas graças à função de ativação ReLU.

Descompressão de GPU

Envie dados compactados do estado z para a GPU e descompacte-os para posterior renderização. Para esse fim, usamos um sombreador computacional simples, que para cada vértice do objeto calcula o produto pontual do vetor z e as três primeiras linhas da matriz UT correspondentes às coordenadas desse vértice, após o qual adicionamos o valor médio x _µ . Essa abordagem tem duas vantagens sobre o método de descompressão ingênuo . Em primeiro lugar, o paralelismo da GPU acelera significativamente o cálculo do vetor de estado do modelo, que pode levar até 1 ms. Em segundo lugar, reduz o tempo de transferência de dados entre a central e a GPU em uma ordem de magnitude, o que é especialmente importante para plataformas nas quais a transferência de todo o estado de todo o objeto é muito lenta.

Previsão normal de vértice

Durante a renderização, não basta ter acesso apenas às coordenadas dos vértices - também são necessárias informações sobre as deformações de suas normais. Geralmente, em um mecanismo físico, omita esse cálculo ou execute um recálculo ingênuo quadro a quadro de normais com sua subsequente redistribuição para os vértices vizinhos. Isso pode se mostrar ineficiente, porque a implementação básica do processador central, além dos custos de descompressão e transferência de dados, requer outros 150 μs para esse procedimento. E, embora esse cálculo possa ser realizado na GPU, ele se torna mais difícil de implementar devido à necessidade de operações paralelas.

Em vez disso, realizamos uma regressão linear do estado do subespaço para vetores de estado completo normais no shader da GPU. Conhecendo os valores das normais dos vértices em cada quadro, calculamos a matriz Q, que melhor representa a representação do subespaço nas normais dos vértices.

Como a previsão de normais em nosso método nunca foi apresentada antes, não há garantia de que essa abordagem seja precisa, mas na prática ela provou ser realmente boa, como pode ser visto na figura abaixo.


Figura 6. Comparação dos modelos calculados pelo nosso método e a referência (verdade fundamental), bem como a diferença entre eles

Luta de interseção

Nossa rede neural aprende a executar colisões com eficiência, no entanto, devido a imprecisões nas previsões e erros causados ​​pela compressão do subespaço, podem ocorrer interseções entre objetos externos e simulados. Além disso, como adiamos o cálculo do estado completo da cena até o início da renderização, não há como resolver esses problemas com antecedência. Portanto, para manter o alto desempenho, é necessário eliminar essas interseções durante a renderização.

Encontramos uma solução simples e eficaz para isso, consistindo no fato de que vértices que se cruzam são projetados na superfície dos primitivos a partir dos quais formamos o personagem. É fácil fazer essa projeção na GPU usando o mesmo sombreador computacional que descompacta o tecido e calcula o sombreamento normal.

Então, em primeiro lugar, comporemos o caractere dos objetos proxy conectados aos vértices com diferentes raios inicial e final, após o qual transferiremos informações sobre as coordenadas e raios desses objetos para o shader computacional. Mais uma vez, verifique as coordenadas de cada vértice quanto à interseção com o objeto proxy correspondente e, se houver, projete esse vértice na superfície do objeto proxy. Portanto, apenas corrigimos a posição do vértice, sem tocar no próprio normal, para não danificar o sombreamento.

Essa abordagem removerá pequenas interseções visíveis de objetos, desde que os erros do deslocamento do vértice não sejam tão grandes que a projeção esteja no lado oposto do objeto proxy correspondente.


Figura 7. Modelo de caractere composto por objetos proxy e os resultados da eliminação de interseções visíveis usando nosso método: antes e depois

Análise de Resultados

Portanto, nossas cenas de teste incluem:

• um avião interagindo com uma bola controlada pelo usuário;
• um plano esticado entre quatro pontos que o usuário pode mover;
• uma bandeira balançando ao vento;
• capa e saia em um personagem animado controlado pelo usuário;
• um coelho sendo atingido por uma bola controlada pelo usuário;
• dragão, sobre o qual a chaleira se move.

Em todos os exemplos, nosso método define a natureza das deformações próximas à natural.

Também realizamos testes de estresse do nosso método em cenas com cem coelhos e 16 caracteres, cada qual modelado de forma independente a uma taxa de quadros de 120 e 240 quadros por segundo.


Figura 8. Teste em 16 caracteres. Hora da festa!

Comparação com o padrão

, , , , .

, PCA. , , , .


9. , , –

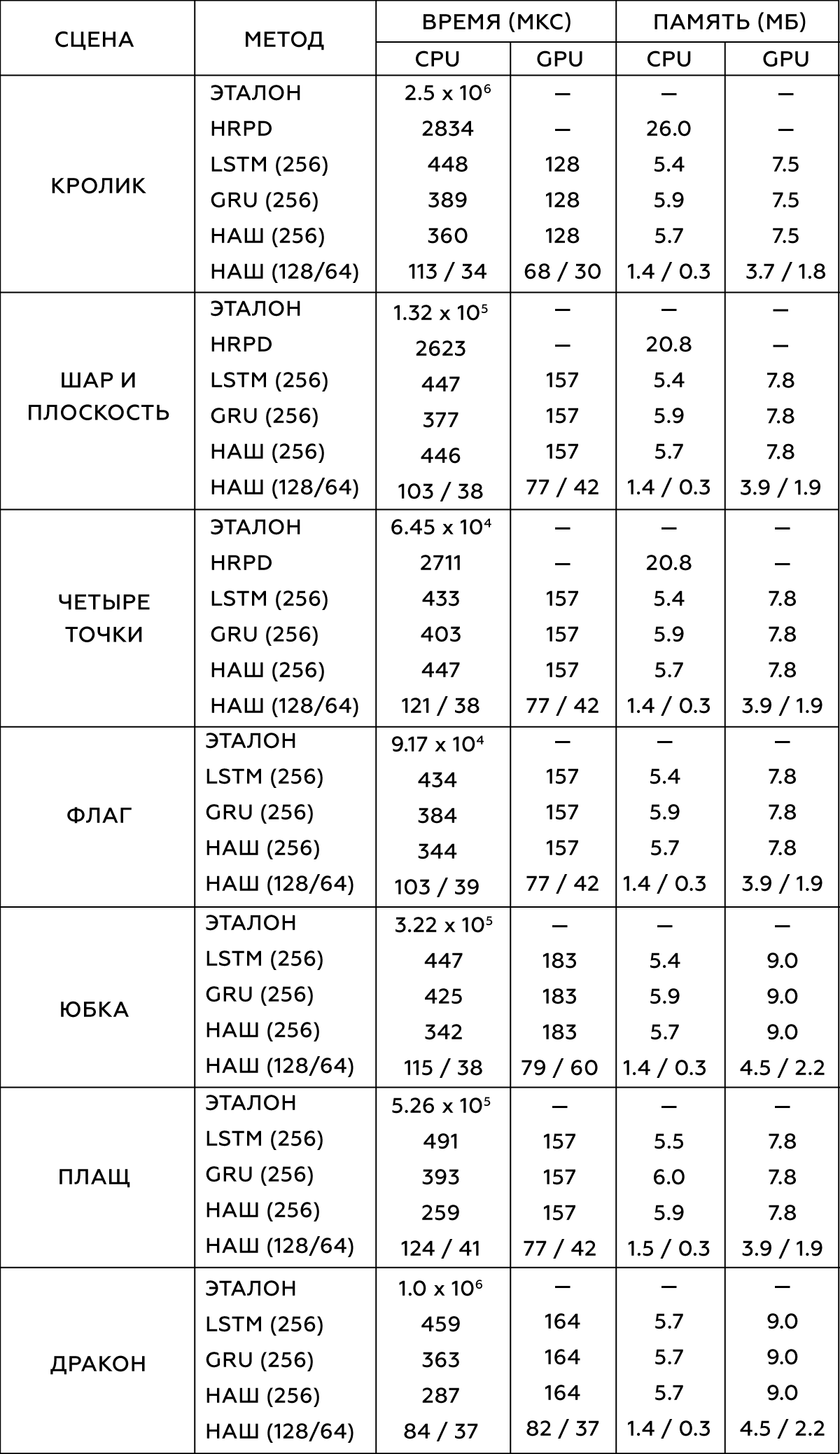
― , . , . 300-5000 , . , - (HRPD) , (LSTM) (GRU) .

, . Intel Xeon E5-1650 3.5 GHz GeForce GTX 1080 Titan.

2.

, , . , .

data-driven , . , , , , , . , , ― , .

, , , .

, . data-driven , ― , . , , , . , , , .

, . .

, , , . , , ― , . -, , , - . .

, , , , . , , , , ― , , . .

.


10. vs : choose your fighter