Trazemos a equação de regressão linear para a forma matricial

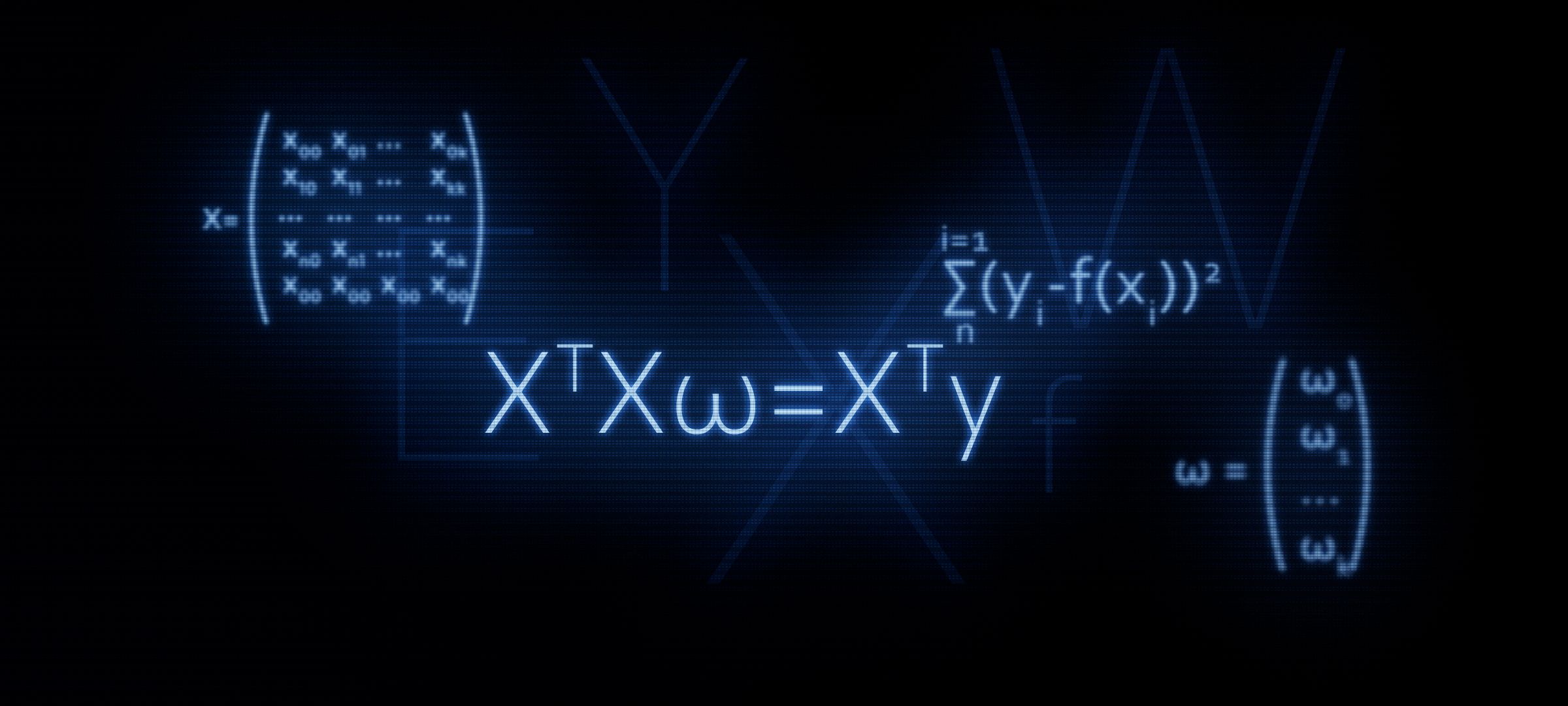
O objetivo do artigo é fornecer suporte a dataintists iniciantes. No artigo anterior, examinamos nos dedos três métodos para resolver a equação de regressão linear: solução analítica, descida em gradiente, descida em gradiente estocástico. Em seguida, para a solução analítica, aplicamos a fórmula $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ . Neste artigo, como segue no título, justificaremos o uso dessa fórmula ou, em outras palavras, derivaremos independentemente.

Por que faz sentido prestar mais atenção à fórmula $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ ?

É com a equação da matriz que, na maioria dos casos, se inicia a regressão linear. Ao mesmo tempo, cálculos detalhados de como a fórmula foi derivada são raros.

Por exemplo, nos cursos de aprendizado de máquina Yandex, quando os alunos são introduzidos à regularização, eles sugerem o uso das funções da biblioteca sklearn , enquanto nenhuma palavra é mencionada sobre a representação matricial do algoritmo. É nesse momento que alguns ouvintes podem querer entender esse problema com mais detalhes - escrever código sem usar funções prontas. E para isso, devemos primeiro apresentar a equação com o regularizador em forma de matriz. Este artigo permitirá que aqueles que desejam dominar essas habilidades. Vamos começar.

Linha de base

Metas

Temos vários valores-alvo. Por exemplo, a meta pode ser o preço de um ativo: petróleo, ouro, trigo, dólar etc. Ao mesmo tempo, por vários valores do indicador de objetivo, queremos dizer o número de observações. Tais observações podem ser, por exemplo, preços mensais do petróleo para o ano, ou seja, teremos 12 valores-alvo. Começamos a introduzir a notação. Designamos cada valor-alvo como $$$y_i$ . Total que temos $$$n$ observações, o que significa que podemos imaginar nossas observações como $$$y_1, y_2, y_3 ... y_n$ .

Regressores

Assumimos que existem fatores que, em certa medida, explicam os valores do indicador de meta. Por exemplo, a taxa de câmbio do par dólar / rublo é fortemente influenciada pelo preço do petróleo, pela taxa do Fed etc. Esses fatores são chamados de regressores. Ao mesmo tempo, cada valor do indicador de meta deve corresponder ao valor do regressor, ou seja, se tivermos 12 metas para cada mês em 2018, também devemos ter 12 regressores para o mesmo período. Indique os valores de cada regressor por $$$x_i: x_1, x_2, x_3 ... x_n$ . Deixe no nosso caso, existe $$$k$ regressores (ou seja, $$$k$ fatores que influenciam o valor do alvo). Portanto, nossos regressores podem ser representados da seguinte forma: para o primeiro regressor (por exemplo, o preço do petróleo): $$$x_ {11}, x_ {12}, x_ {13} ... x_ {1n}$ , para o segundo regressor (por exemplo, a taxa do Fed): $$$x_ {21}, x_ {22}, x_ {23} ... x_ {2n}$ para $$$k$ th "regressor: $$$x_ {k1}, x_ {k2}, x_ {k3} ... x_ {kn}$

Dependência de alvos em regressores

Assumir dependência de destino $$$y_i$ dos regressores " $$$i$ -a "observação pode ser expressa através da equação de regressão linear da forma:

$$

$$f (w, x_i) = w_0 + w_1 x_ {1i} + ... + w_k x_ {ki}$$

onde $$$x_i$ - " $$$i$ th "valor do regressor de 1 a $$$n$ ,

$$$k$ - o número de regressores de 1 a $$$k$

$$$w$ - coeficientes angulares que representam a quantidade pela qual o indicador de meta calculado mudará em média quando o regressor for alterado.

Em outras palavras, somos a favor de todos (exceto $$$w_0$ ) do regressor, determinamos o coeficiente "nosso" $$$w$ , multiplique os coeficientes pelos valores dos regressores " $$$i$ -ª "observação, como resultado, temos uma certa aproximação" $$$i$ th "alvo.

Portanto, precisamos selecionar esses coeficientes $$$w$ para os quais os valores da nossa função de aproximação $$$f (w, x_i)$ será localizado o mais próximo possível dos valores dos alvos.

Estimativa da qualidade da função de aproximação

Determinaremos a estimativa de qualidade da função de aproximação pelo método dos mínimos quadrados. A função de avaliação da qualidade, neste caso, assumirá a seguinte forma:

$$

$$Err = \ soma \ limites_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ rightarrow min$$

Precisamos escolher esses valores dos coeficientes $ w $ para os quais o valor $$$Err$ será o menor.

Traduzimos a equação em forma de matriz

Vista vetorial

Primeiro, para facilitar sua vida, você deve prestar atenção à equação de regressão linear e observar que o primeiro coeficiente $$$w_0$ não multiplicado por nenhum regressor. Além disso, quando traduzimos os dados em forma de matriz, a circunstância acima complicará seriamente os cálculos. Nesse sentido, propõe-se a introdução de outro regressor para o primeiro coeficiente $$$w_0$ e igualar a um. Ou melhor, cada " $$$i$ o "valor" desse regressor para igualar a unidade - porque, quando multiplicado pela unidade, nada mudará em termos do resultado dos cálculos e, do ponto de vista das regras para o produto das matrizes, nosso tormento será reduzido significativamente.

Agora, por um tempo, para simplificar o material, suponha que tenhamos apenas um " $$$i$ th "observação. Então, imagine os valores dos regressores" $$$i$ th observação como um vetor $$$\ vec {x_i}$ . Vetor $$$\ vec {x_i}$ tem dimensão $$$(k \ vezes 1)$ isso é $$$k$ linhas e 1 coluna:

$$

$$\ vec {x_i} = \ begin {pmatrix} x_ {0i} \\ x_ {1i} \\ ... \\ x_ {ki} \ end {pmatrix} \ qquad$$

Os coeficientes desejados podem ser representados como um vetor $$$\ vec {w}$ tendo dimensão $$$(k \ vezes 1)$ :

$$

$$\ vec {w} = \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$$

A equação de regressão linear para " $$$i$ -a "observação assumirá a forma:

$$

$$f (w, x_i) = \ vec {x_i} ^ T \ vec {w}$$

A função de avaliação da qualidade do modelo linear assumirá a forma:

$$

$$Err = \ soma \ limites_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 \ rightarrow min$$

Observe que, de acordo com as regras de multiplicação de matrizes, é necessário transpor o vetor $$$\ vec {x_i}$ .

Representação matricial

Como resultado da multiplicação de vetores, obtemos o número: $$$(1 \ vezes k) \ ponto central (k \ vezes 1) = 1 \ vezes 1$ como esperado. Este número é a aproximação " $$$i$ -ésimo "alvo. Mas precisamos aproximar não um valor do alvo, mas todos. Para fazer isso, escrevemos tudo" $$$i$ regressores matriciais $$$X$ . A matriz resultante tem a dimensão $$$(n \ vezes k)$ :

$$exibição $$ $$ X = \ begin {pmatrix} x_ {00} e x_ {01} e ... & x_ {0k} \\ x_ {10} e x_ {11} e ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} e x_ {n1} e ... & x_ {nk} \ end {pmatrix} \ qquad $$ display $$

Agora a equação de regressão linear assumirá a forma:

$$

$$f (w, X) = X \ vec {w}$$

Indique os valores dos indicadores alvo (todos $$$y_i$ ) por vetor $$$\ vec {y}$ dimensão $$$(n \ vezes 1)$ :

$$

$$\ vec {y} = \ begin {pmatrix} y_ {0} \\ y_ {1} \\ ... \\ y_ {n} \ end {pmatrix} \ qquad$$

Agora podemos escrever no formato de matriz a equação para avaliar a qualidade de um modelo linear:

$$

$$Err = (X \ vec {w} - \ vec {y}) ^ 2 \ rightarrow min$$

Na verdade, a partir desta fórmula, obtemos ainda a fórmula conhecida por nós $$$X ^ T X w = X ^ T y$

Como isso é feito? Os colchetes são abertos, a diferenciação é realizada, as expressões resultantes são transformadas, etc., e é isso que vamos fazer agora.

Transformações matriciais

Expanda os colchetes

$$$(X \ vec {w} - \ vec {y}) ^ 2 = (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y})$

$$$= (X \ vec {w}) ^ TX \ vec {w} - \ vec {y} ^ TX \ vec {w} - (X \ vec {w}) ^ T \ vec {y} + \ vec { y} ^ T \ vec {y}$

Prepare uma equação para diferenciação

Para isso, realizamos algumas transformações. Nos cálculos subsequentes, será mais conveniente para nós se o vetor $$$\ vec {w} ^ T$ será apresentado no início de cada trabalho na equação.

Conversão 1

$$$\ vec {y} ^ TX \ vec {w} = (X \ vec {w}) ^ T \ vec {y} = \ vec {w} ^ TX ^ T \ vec {y}$

Como isso aconteceu? Para responder a essa pergunta, basta olhar para os tamanhos das matrizes multiplicadas e ver que, na saída, obtemos um número ou não $$$const$ .

Escrevemos as dimensões das expressões da matriz.

$$$\ vec {y} ^ TX \ vec {w}: (1 \ vezes n) \ ponto central (n \ vezes k) \ ponto central (k \ vezes 1) = (1 \ vezes 1) = const$

$$$(X \ vec {w}) ^ T \ vec {y}: ((n \ vezes k) \ ponto central (k \ vezes 1)) ^ T \ ponto central (n \ vezes 1) = (1 \ vezes n) \ centerdot (n \ vezes 1) = (1 \ vezes 1) = const$

$$$\ vec {w} ^ TX ^ T \ vec {y}: (1 \ vezes k) \ ponto central (k \ vezes n) \ ponto central (n \ vezes 1) = (1 \ vezes 1) = const$

Conversão 2

$$$(X \ vec {w}) ^ TX \ vec {w} = \ vec {w} ^ TX ^ TX \ vec {w}$

Escrevemos de maneira semelhante à transformação 1

$$$(X \ vec {w}) ^ TX \ vec {w}: ((n \ vezes k) \ ponto central (k \ vezes 1)) ^ T \ ponto central (n \ vezes k) \ ponto central (k \ vezes 1 ) = (1 \ vezes 1) = const$

$$$\ vec {w} ^ TX ^ TX \ vec {w}: (1 \ vezes k) \ ponto central (k \ vezes n) \ ponto central (n \ vezes k) \ ponto central (k \ vezes 1) = (1 \ vezes 1) = const$

Na saída, obtemos uma equação que precisamos diferenciar:
$$$Err = \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

Diferenciamos a função de avaliar a qualidade do modelo

Diferenciar por vetor $$$\ vec {w}$ :

$$

$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}}$$

$$$(\ vec {w} ^ TX ^ TX \ vec {w}) '- (2 \ vec {w} ^ TX ^ T \ vec {y})' + (\ vec {y} ^ T \ vec {y }) '= 0$

$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} + 0 = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

Perguntas por que $$$(\ vec {y} ^ T \ vec {y}) '= 0$ não deveria ser, mas as operações para determinar as derivadas nas outras duas expressões, analisaremos mais detalhadamente.

Diferenciação 1

Revelamos a diferenciação: $$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w})} {d \ vec {w}} = 2X ^ TX \ vec {w}$

Para determinar a derivada de uma matriz ou vetor, você precisa ver o que eles têm dentro. Nós olhamos:

$$$ inline $ \ vec {w} ^ T = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$\ vec {w} = \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$

$$$ inline $ X ^ T = \ begin {pmatrix} x_ {00} e x_ {10} e ... & x_ {n0} \\ x_ {01} & x_ {11} e ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} e x_ {1k} e ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $$$ $ inline $ X = \ begin {pmatrix} x_ {00} e x_ {01} e ... & x_ {0k} \\ x_ {10} e x_ {11} e ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

Denotar o produto de matrizes $$$X ^ TX$ através da matriz $$$A$ . Matrix $$$A$ quadrado e, além disso, é simétrico. Essas propriedades serão úteis para nós ainda mais, lembre-se delas. Matrix $$$A$ tem dimensão $$$(k \ vezes k)$ :

$$$ inline $ A = \ begin {pmatrix} a_ {00} e a_ {01} e ... & a_ {0k} \\ a_ {10} e a_ {11} e ... & a_ {1k} \\ ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad $ inline $

Agora, nossa tarefa é multiplicar corretamente os vetores pela matriz e não obter "duas vezes dois cinco", para que possamos nos concentrar e ser extremamente cuidadosos.

$$$ inline $ \ vec {w} ^ TA \ vec {w} = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad \ times \ begin {pmatrix} a_ {00} e a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \ \ a_ {k0} e a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$ inline $ = \ begin {pmatrix} w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0} & ... & w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk} \ end {pmatrix} \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$= \ begin {pmatrix} (w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0}) w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu (w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk}) w_k \ end {pmatrix} =$

$$$= w_0 ^ 2a_ {00} + w_1a_ {10} w_0 + w_ka_ {k0} w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_0a_ {0k} w_k + w_1a_ {1k} w_k + .. . + w_k ^ 2a_ {kk}$

No entanto, temos uma expressão complexa! De fato, temos um número - um escalar. E agora, já de verdade, passamos à diferenciação. É necessário encontrar a derivada da expressão obtida para cada coeficiente $$$w_0 w_1 ... w_k$ e obtenha o vetor de dimensão na saída $$$(k \ vezes 1)$ . Apenas no caso, descreverei os procedimentos para as ações:

1) diferenciar por $$$w_o$ nós obtemos: $$$2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k}$

2) diferenciar por $$$w_1$ nós obtemos: $$$w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ {k}$

3) diferenciar por $$$w_k$ nós obtemos: $$$w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k-1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk}$

Na saída, o vetor prometido de tamanho $$$(k \ vezes 1)$ :

$$

$$\ begin {pmatrix} 2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k} \\ w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ { k} \\ ... \\ ... \\ ... \\ w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k -1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk} \ end {pmatrix}$$

Se você olhar mais de perto o vetor, notará que os elementos esquerdo e direito do vetor correspondentes podem ser agrupados de forma que, como resultado, o vetor possa ser distinguido do vetor apresentado $$$\ vec {w}$ o tamanho $$$(k \ vezes 1)$ . Por exemplo $$$w_1a_ {10}$ (elemento esquerdo da linha superior do vetor) $$$+ a_ {01} w_1$ (o elemento direito da linha superior do vetor) pode ser representado como $$$w_1 (a_ {10} + a_ {01})$ e $$$w_2a_ {20} + a_ {02} w_2$ - como $$$w_2 (a_ {20} + a_ {02})$ etc. em cada linha. Grupo:

$$

$$\ begin {pmatrix} 2w_0a_ {00} + w_1 (a_ {10} + a_ {01}) + w_2 (a_ {20} + a_ {02}) + ... + w_k (a_ {k0} + a_ { 0k}) \\ w_0 (a_ {01} + a_ {10}) + 2w_1a_ {11} + w_2 (a_ {21} + a_ {12}) + ... + w_k (a_ {k1} + a_ {1k }) \\ ... \\ ... \\ ... \\ w_0 (a_ {0k} + a_ {k0}) + w_1 (a_ {1k} + a_ {k1}) + w_2 (a_ {2k } + a_ {k2}) + ... + 2w_ka_ {kk} \ end {pmatrix}$$

Retire o vetor $$$\ vec {w}$ e na saída temos:

$$exibição $$ $$ \ begin {pmatrix} 2a_ {00} e a_ {10} + a_ {01} e a_ {20} + a_ {02} e ... & a_ {k0} + a_ {0k} \\ a_ {01} + a_ {10} e 2a_ {11} e a_ {21} + a_ {12} e ... & a_ {k1} + a_ {1k} \\ ... & ... & .. . & ... & ... \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & .. & .. . \\ a_ {0k} + a_ {k0} e a_ {1k} + a_ {k1} e a_ {2k} + a_ {k2} & ... & 2a_ {kk} \ end {pmatrix} \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ ... \\ ... \\ w_k \ end {pmatrix} \ qquad $$ display $$

Agora, vamos dar uma olhada na matriz resultante. Uma matriz é a soma de duas matrizes $$$A + A ^ T$ :

$$exibição $$ $$ \ begin {pmatrix} a_ {00} e a_ {01} e a_ {02} e ... & a_ {0k} \\ a_ {10} e a_ {11} e a_ {12} e ... & a_ {1k} \\ ... & ... & ... & ... & ... \\ a_ {k0} & a_ {k1} e a_ {k2} & ... & a_ {kk} \ end {pmatrix} + \ begin {pmatrix} a_ {00} e a_ {10} e a_ {20} e ... & a_ {k0} \\ a_ {01} e a_ {11} e a_ {21} & ... & a_ {k1} \\ ... & ... & ... & ... & ... \\ a_ {0k} e a_ {1k} e a_ {2k} & ... & a_ {kk} \ end {pmatrix} \ qquad $$ display $$

Lembre-se que, um pouco antes, observamos uma propriedade importante da matriz $$$A$ - é simétrico. Com base nessa propriedade, podemos afirmar com confiança que a expressão $$$A + A ^ T$ é igual a $$$2A$ . Isso é fácil de verificar, revelando o produto matriz por elemento $$$X ^ TX$ . Não faremos isso aqui, aqueles que desejarem podem realizar uma verificação por conta própria.

Vamos voltar à nossa expressão. Após nossas transformações, aconteceu como queríamos vê-lo:

$$

$$(A + A ^ T) \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = 2A \ vec {w} = 2X ^ TX \ vec {w}$$

Então, lidamos com a primeira diferenciação. Passamos para a segunda expressão.

Diferenciação 2

$$$\ frac {d (2 \ vec {w} ^ TX ^ T \ vec {y})} {d \ vec {w}} = 2X ^ T \ vec {y}$

Vamos seguir o caminho batido. Será muito mais curto que o anterior, portanto, não vá longe da tela.

Nós revelamos os vetores e a matriz elemento a elemento:

$$$ inline $ \ vec {w} ^ T = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$ inline $ X ^ T = \ begin {pmatrix} x_ {00} e x_ {10} e ... & x_ {n0} \\ x_ {01} & x_ {11} e ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} e x_ {1k} e ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

$$$\ vec {y} = \ begin {pmatrix} y_0 \\ y_1 \\ ... \\ y_n \ end {pmatrix} \ qquad$

Por um tempo, removemos o empate dos cálculos - ele não desempenha um grande papel, depois o devolvemos ao seu lugar. Multiplique os vetores pela matriz. Primeiro de tudo, multiplicamos a matriz $$$X ^ T$ em vetor $$$\ vec {y}$ , aqui não temos restrições. Obtenha o vetor de tamanho $$$(k \ vezes 1)$ :

$$

$$\ begin {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

Execute a seguinte ação - multiplique o vetor $$$\ vec {w}$ para o vetor resultante. Na saída, um número nos espera:

$$

$$\ begin {pmatrix} w_0 (x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n) + w_1 (x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1 } y_n) \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_k (x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n) \ end {pmatrix} \ qquad$$

Nós então o diferenciamos. Na saída, obtemos um vetor de dimensão $$$(k \ vezes 1)$ :

$$

$$\ begin {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

Parece algo? Tudo bem! Este é o produto da matriz. $$$X ^ T$ em vetor $$$\ vec {y}$ .

Assim, a segunda diferenciação foi concluída com sucesso.

Em vez de uma conclusão

Agora sabemos como surgiu a igualdade. $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ .

Por fim, descrevemos uma maneira rápida de transformar as principais fórmulas.

Estime a qualidade do modelo de acordo com o método dos mínimos quadrados:
$$$\ sum \ limits_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ mkern 20mu = \ mkern 20mu \ sum \ limits_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 =$

$$$= (X \ vec {w} - \ vec {y}) ^ 2 \ mkern 20mu = \ mkern 20mu (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y}) \ mkern 20mu = \ mkern 20mu \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

Diferenciamos a expressão resultante:
$$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}} =$$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

$$$\ leftarrow$ Trabalho anterior do autor - “Resolvemos a equação da regressão linear simples”
$$$\ rightarrow$ O próximo trabalho do autor - "Chewing Regression Logistic"

Literatura

Fontes da Internet:

1) habr.com/en/post/278513
2) habr.com/ru/company/ods/blog/322076
3) habr.com/en/post/307004
4) nabatchikov.com/blog/view/matrix_der

Livros didáticos, coleções de tarefas:

1) Notas de aula sobre matemática superior: curso completo / D.T. Escrito - 4ª ed. - M: Iris Press, 2006
2) Análise de Regressão Aplicada / N. Draper, G. Smith - 2a ed. - M .: Finanças e estatística, 1986 (traduzido do inglês)
3) Tarefas para resolver equações matriciais:
function-x.ru/matrix_equations.html
mathprofi.ru/deistviya_s_matricami.html