Ao extrair informações, muitas vezes surge a tarefa de encontrar esses fragmentos de texto. No contexto de uma pesquisa, uma consulta pode ser gerada pelo usuário (por exemplo, o texto que o usuário digita no mecanismo de pesquisa) ou pelo próprio sistema. Frequentemente, precisamos corresponder uma consulta recebida com consultas já indexadas. Neste artigo, veremos como você pode criar um sistema que resolva esse problema em relação a bilhões de solicitações sem gastar uma fortuna na infraestrutura do servidor.

Primeiro, definimos formalmente o problema:

Dado um conjunto fixo de consultas $$$Q$ pedido recebido $$$q$ e inteiro $$$k$ . Precisa encontrar esse subconjunto de consultas $$$R = \ left \ {q0, q1, ..., qk \ right \} \ subconjunto Q$ para cada solicitação $$$q_ {i} \ em R$ era mais como $$$q$ do que qualquer outro pedido em $$$Q ∖ R$ .

Por exemplo, com este conjunto de consultas $$$Q$ :

{tesla cybertruck, beginner bicycle gear, eggplant dishes, tesla new car, how expensive is cybertruck, vegetarian food, shimano 105 vs ultegra, building a carbon bike, zucchini recipes} 

e $$$k = 3$ Você pode esperar este resultado:


Observe que ainda não definimos um critério de similaridade . Nesse contexto, isso pode significar quase tudo, mas geralmente se resume a alguma forma de similaridade com base em palavras-chave ou vetores. Usando similaridade com base em palavras-chave, podemos encontrar duas consultas semelhantes se elas contiverem palavras comuns suficientes. Por exemplo, as consultas "abrir um restaurante em munique" e "melhor restaurante de munique" são semelhantes porque contêm as palavras "restaurante" e "munique". E as perguntas "melhor restaurante de munique" e "onde comer em munique" já são menos semelhantes, porque têm apenas uma palavra comum. No entanto, quem procura um restaurante em Munique ficaria melhor se o segundo par de pedidos fosse semelhante. E nisso ajudaremos a comparação com base em vetores.

Representação vetorial de palavras

A representação vetorial de palavras é uma técnica de aprendizado de máquina usada no processamento de linguagem natural para converter texto ou palavras em vetores. Movendo a tarefa para o espaço vetorial, podemos usar operações matemáticas com vetores - somando e calculando distâncias. Para estabelecer links entre palavras semelhantes, você pode usar métodos tradicionais de agrupamento de vetores. O significado dessas operações no espaço de palavras original pode não ser óbvio, mas a vantagem é que agora temos acesso a uma ampla gama de ferramentas matemáticas. Se você estiver interessado em detalhes sobre vetores de palavras e sua aplicação, leia sobre word2vec e GloVe .

Temos uma maneira de gerar vetores a partir de palavras, agora vamos reuni-los em vetores de texto (vetores de documentos ou expressões). A maneira mais fácil de fazer isso é adicionando (ou calculando a média) os vetores de todas as palavras no texto.


^{Figura 1: Vetores de consulta.}

Agora você pode determinar a semelhança de duas partes do texto (ou consultas) representando-as no espaço vetorial e calculando a distância entre os vetores. Normalmente, uma distância angular é usada para isso.

Como resultado, a representação vetorial de palavras permite a correspondência textual de um tipo diferente, que complementa a correspondência baseada em palavras-chave. Você pode explorar a semelhança semântica dos pedidos (por exemplo, "melhor restaurante de munique" e "onde comer em munique"), como não podíamos fazer antes.

Pesquisa por Vizinho Mais Próximo Aproximado

Agora podemos refinar nosso problema de correspondência de consulta original:

Dado um conjunto fixo de vetores de consulta $$$Q$ vetor de entrada $$$q$ e inteiro $$$k$ . Você precisa encontrar esse subconjunto de vetores $$$R = \ left \ {q0, q1, ..., qk \ right \} \ subconjunto Q$ de modo que a distância angular de $$$q$ para cada vetor $$$q_ {i} \ em R$ foi menor que a distância para qualquer outro vetor $$$Q ∖ R$ .

Isso é chamado de tarefa de encontrar o vizinho mais próximo. Existem vários algoritmos para sua solução rápida em espaços de baixa dimensão. Porém, ao trabalhar com representações vetoriais de palavras, geralmente operamos com vetores de alta dimensão (100-1000 dimensões). E aqui os métodos mencionados não funcionam mais.

Não existe uma maneira adequada de determinar rapidamente os vizinhos mais próximos em espaços de alta dimensão. Portanto, simplificamos o problema permitindo o uso de resultados aproximados: em vez de sempre retornar os vetores mais próximos, ficaremos satisfeitos com apenas alguns dos vizinhos mais próximos ou até certo ponto próximos. Isso é chamado de tarefa de busca aproximada dos vizinhos mais próximos e é uma área de pesquisa ativa.

Mundo pequeno hierárquico

O gráfico de mundo pequeno navegável hierárquico ( HNSW ) é um dos algoritmos mais rápidos para a pesquisa aproximada dos vizinhos mais próximos. O índice de pesquisa no HNSW é uma estrutura de vários níveis, na qual cada nível é um gráfico de proximidade. Cada nó do gráfico corresponde a um dos vetores de consulta.


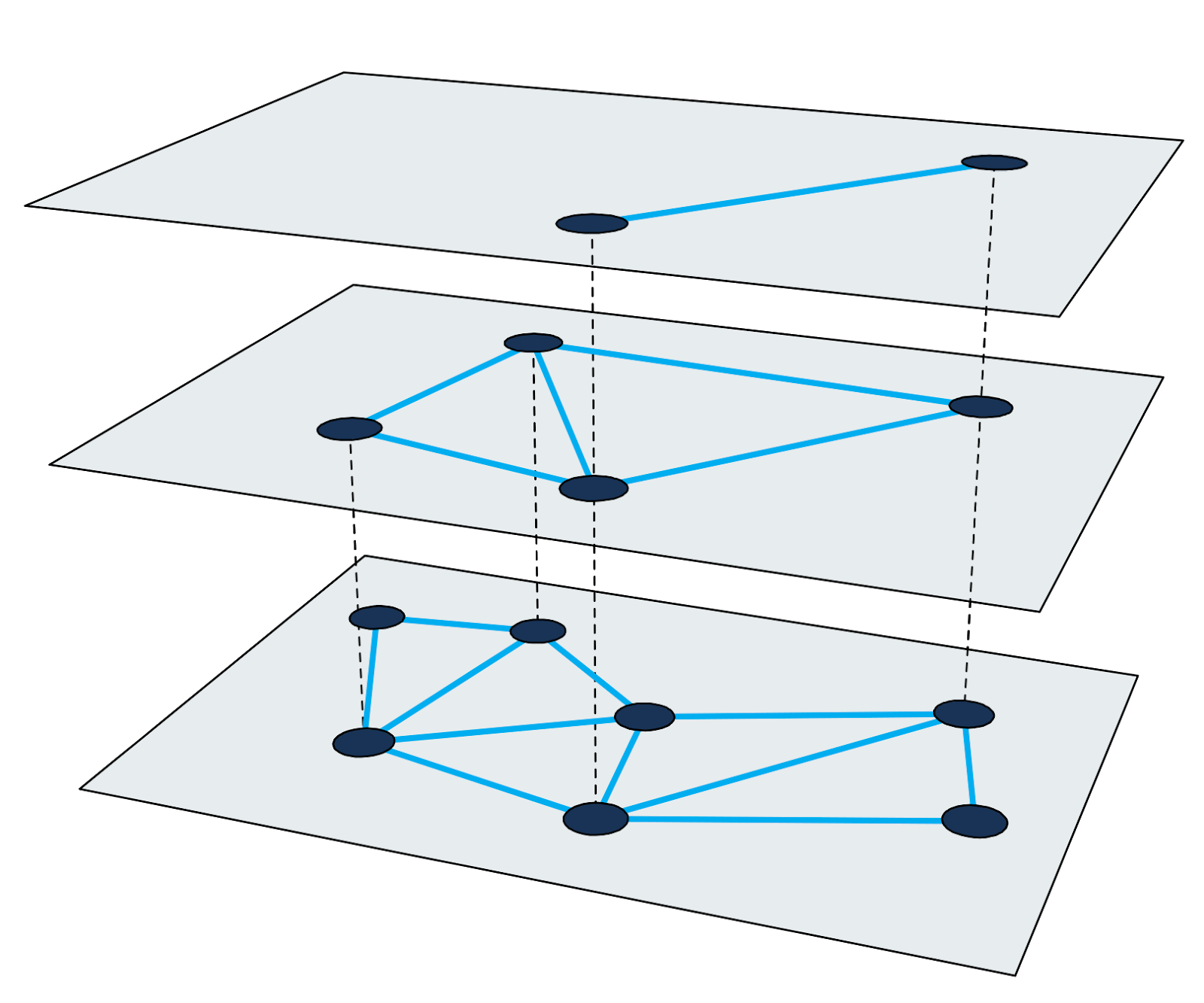^{Figura 2: Gráfico de proximidade multinível.}
Encontrar vizinhos mais próximos no HNSW usa o método de aumento de zoom. Ele inicia no nó de entrada do nível mais alto e executa recursivamente o percurso de gráfico ganancioso em cada nível até atingir um mínimo local na parte inferior.

Detalhes sobre o algoritmo e a técnica de pesquisa estão bem descritos no trabalho científico. É importante lembrar que cada ciclo de pesquisa dos vizinhos mais próximos consiste em percorrer os nós dos gráficos e calcular as distâncias entre os vetores. Examinaremos essas etapas abaixo para usar esse método para criar um índice em larga escala.

A dificuldade de indexar bilhões de consultas

Suponha que precisamos indexar 4 bilhões de vetores de consulta 200-dimensionais, com cada dimensão representada por um número de ponto flutuante de quatro bytes (4 bilhões são suficientes para tornar a tarefa interessante, mas você ainda pode armazenar os IDs dos nós em números regulares de quatro bytes) . Um cálculo aproximado indica que o tamanho dos vetores será de aproximadamente 3 TB. Como a maioria das bibliotecas existentes usa uma capacidade de RAM para uma pesquisa aproximada dos vizinhos mais próximos, precisaremos de um servidor muito grande para inserir pelo menos vetores na RAM. Observe que isso não leva em consideração o índice de pesquisa adicional, necessário para a maioria dos métodos.

Em toda a história do desenvolvimento de nosso mecanismo de pesquisa, usamos várias abordagens diferentes para resolver esse problema. Vamos considerar alguns deles.

Subconjunto de dados

A primeira e mais simples abordagem, que não nos permitiu resolver completamente o problema, foi limitar o número de vetores no índice. Tomando um décimo dos dados, criamos um índice que precisa - surpresa - 10% da memória. No entanto, a qualidade da pesquisa se deteriorou, porque agora operamos com menos consultas.

Quantização

Aqui, usamos todos os dados, mas os reduzimos usando a quantização (usamos diferentes técnicas de quantização, por exemplo, quantização do produto, mas não conseguimos atingir a qualidade desejada de trabalho com essa quantidade de dados). Ao arredondar alguns erros, conseguimos substituir todos os números de quatro bytes nos vetores originais por versões quantizadas de um byte. A quantidade de RAM para vetores diminuiu 75%. No entanto, ainda precisávamos de 750 GB de memória (sem contar o tamanho do próprio índice), e este ainda é um servidor muito grande.

Resolvendo problemas de memória com o Granne

As abordagens descritas tiveram suas vantagens, mas exigiram muitos recursos e deram baixa qualidade à pesquisa. Embora existam bibliotecas que respondem em menos de 1 ms, poderíamos sacrificar a velocidade em troca de requisitos de hardware mais baixos.

Granne (vizinhos mais próximos aproximados baseados em gráficos) é uma biblioteca HNSW desenvolvida e usada pela Cliqz para pesquisar essas consultas. Possui código-fonte aberto, mas a biblioteca ainda está em desenvolvimento ativo. Uma versão melhorada será publicada no crates.io em 2020. Está escrito em Rust com inserções Python, projetado para lidar com bilhões de vetores usando competitividade. Do ponto de vista dos vetores de consulta, é interessante que o Granne tenha um modo especial que exija muito menos memória em comparação com outras bibliotecas.

Representação compacta de vetores de consulta

Reduzir o tamanho dos vetores de consulta nos dará muitos benefícios. Para fazer isso, vamos voltar e considerar a criação de vetores. Como as consultas são compostas de palavras e os vetores de consulta são somas de vetores de palavras, podemos recusar explicitamente o armazenamento de vetores de consulta e calculá-los conforme necessário.

Você pode armazenar consultas na forma de conjuntos de palavras e usar a tabela de pesquisa para encontrar os vetores correspondentes. No entanto, evitamos o redirecionamento armazenando cada consulta como uma lista de IDs inteiros correspondentes aos vetores de palavras na consulta. Por exemplo, salve a consulta "melhor restaurante de munique" como $$$[{i_ {best}}, {i_ {restaurant}}, {i_ {of}}, {i_ {munich}}]$ onde $$${i_ {best}}$ - esse é o ID do vetor da palavra "melhor" etc. Suponha que tenhamos menos de 16 milhões de vetores de palavras (mais do que esse valor custará 1 byte por palavra), então você pode usar 3 bytes para representar todos os IDs de palavras. Ou seja, em vez de armazenar 800 bytes (ou 200 bytes no caso de vetores quantizados), armazenaremos apenas 12 bytes para esta solicitação (isso não é totalmente verdade. Como as solicitações consistem em um número diferente de palavras, também precisamos armazenar o deslocamento da lista no índice de palavras. isso exigirá 5 bytes por solicitação).

Quanto aos vetores de palavras, todos precisamos deles. No entanto, o número de palavras é muito menor que o número de consultas que podem ser criadas combinando essas palavras. E isso significa que o tamanho das palavras não é tão importante. Se você armazenar vetores de palavras como versões de ponto flutuante de quatro bytes em uma matriz simples $$$v$ , precisamos de menos de 1 GB para cada milhão de palavras. Este volume pode caber facilmente na RAM. Agora, o vetor de consulta fica assim: $$${v _ {{i_ {best}}}} + {v _ {{i_ {restaurant}}} + {v _ {{i_ {of}}} + {v _ {{i_ {munich}}}}$ .

O tamanho final do envio da consulta depende do número total de palavras na consulta. Para 4 bilhões de consultas, são cerca de 80 GB (incluindo vetores de palavras). Em outras palavras, comparado aos vetores de palavras originais, o tamanho diminuiu 97% e comparado aos vetores quantizados - 90%.

E mais uma coisa. Para uma pesquisa, precisamos visitar aproximadamente 200 a 300 nós do gráfico. Cada nó tem 20 a 30 vizinhos. Portanto, precisamos calcular a distância do vetor de consulta de entrada aos 4000-9000 vetores no índice. E mais, precisamos gerar vetores. Quanto tempo leva para criar vetores de consulta rapidamente?

Acontece que, com um processador relativamente novo, esse problema pode ser resolvido em alguns milissegundos. Uma solicitação que costumava ser executada em 1 ms agora é executada em cerca de 5 ms. Mas reduzimos a quantidade de memória para vetores em 90%. Aceitamos com prazer esse compromisso.

Exibir na memória de vetores e índice

Acima, resolvemos o problema de reduzir a quantidade de memória para vetores. Mas depois que resolvemos esse problema, a própria estrutura do índice se tornou um fator limitante. Agora você precisa reduzir seu tamanho.

No Granne, a estrutura do gráfico é armazenada compactamente na forma de uma lista de adjacências com um número variável de vizinhos para cada nó. Ou seja, a memória dificilmente é desperdiçada em metadados. O tamanho da estrutura do índice depende muito dos parâmetros de design e das propriedades do gráfico. No entanto, para ter uma idéia do tamanho do índice, basta dizer que podemos criar um índice para 4 bilhões de vetores com um tamanho total de cerca de 240 GB. Isso pode ser aceitável para uso na memória em um servidor grande, mas pode ser feito melhor.


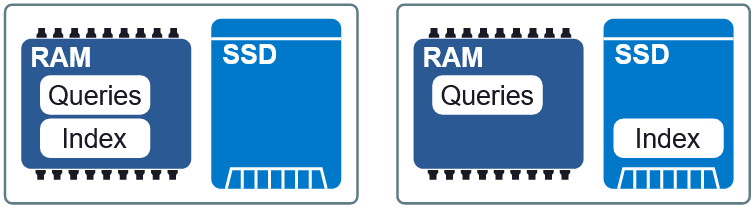^{Figura 3: Dois layouts diferentes na RAM e SSD.}

Uma propriedade importante do Granne é a capacidade de exibir os vetores de índice e consulta na memória . Isso nos permite carregar preguiçosamente o índice e compartilhar memória com vários processos. Os arquivos de índice e consulta são divididos em arquivos de exibição separados na memória e podem ser usados ​​em diferentes layouts na RAM e no SSD. Se os requisitos para o atraso forem um pouco menores, então, colocando o índice no SSD, solicitações para RAM, mantemos uma velocidade aceitável sem consumo excessivo de memória. No final do artigo, veremos como esse compromisso se parece.

Melhorando a localidade dos dados

Em nossa configuração atual, quando o índice está em um SSD, cada solicitação requer de 200 a 300 leituras do disco. Você pode tentar aumentar a localidade dos dados organizando os elementos cujos vetores estão tão próximos que seus nós HNSW estão localizados no índice também não muito longe um do outro. A localidade dos dados melhora o desempenho, porque é mais provável que uma operação de leitura única (geralmente extraída de 4 KB) contenha outros nós necessários para percorrer o gráfico. E isso, por sua vez, reduz o número de recuperações de dados por uma pesquisa.


^{Figura 4: A localidade dos dados reduz a recuperação de informações.}

Deve-se notar que os elementos de reordenação não afetam os resultados da pesquisa; é uma maneira de acelerar isso. Ou seja, o pedido pode ser qualquer, mas nem todas as opções aceleram a pesquisa. É muito difícil encontrar a ordem ideal. No entanto, a heurística que usamos com sucesso é classificar as consultas pela palavra mais importante em cada consulta.

Conclusão

Usamos o Granne para criar e manter índices de bilhões de dólares com vetores de consulta, a fim de procurar consultas semelhantes com consumo de memória relativamente baixo. A tabela abaixo mostra os requisitos para diferentes métodos. Seja cético em relação aos valores absolutos dos atrasos durante a pesquisa, porque eles dependem fortemente do que é considerado uma resposta aceitável. No entanto, essas informações descrevem o desempenho relativo dos métodos.


* A alocação de um índice de memória maior que a quantidade necessária levou ao cache de alguns nós (frequentemente visitados), o que reduziu o atraso na pesquisa. Nenhum cache interno foi usado para isso, apenas ferramentas internas do SO (kernel do Linux).

Deve-se notar que algumas das otimizações mencionadas no artigo não são aplicáveis ​​para resolver o problema geral de encontrar vizinhos mais próximos com vetores indecomponíveis. No entanto, eles são aplicáveis ​​em qualquer situação em que os elementos possam ser gerados a partir de menos partes (como é o caso de palavras e consultas). Caso contrário, você ainda poderá usar o Granne com os vetores de origem, mas será necessário mais memória, como em outras bibliotecas.