Às vezes, surge uma tarefa para "colar" uma seleção integral com os mesmos dados "em colunas" das matrizes lineares passadas como parâmetros na consulta SQL.
Como é feito às vezes:
WITH T1 AS ( SELECT row_number() OVER() rn , unnest v1 FROM unnest('{1,2,3,4}'::integer[]) ) , T2 AS ( SELECT row_number() OVER() rn , unnest v2 FROM unnest('{5,6}'::integer[]) ) SELECT T1.v1 , T2.v2 FROM T1 LEFT JOIN T2 USING(rn);
v1 | v2 ------- 1 | 5 2 | 6 3 | 4 |
Ou seja, primeiro, cada uma das matrizes foi "expandida" na amostra, numerada e, em seguida, esse número foi usado como a chave de conexão CTE ...
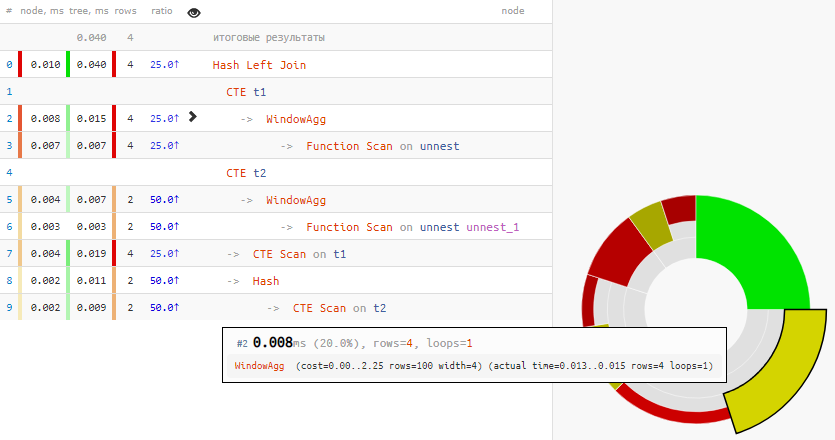 [veja em explicar.tensor.ru]
[veja em explicar.tensor.ru]COM ORDINALIDADE
Mais de um quarto de todo o tempo foi gasto em um par de WindowAgg!
Mas se usarmos uma versão do PG não inferior a 9.4,
poderemos usar WITH ORDINALITY para numerar os resultados de qualquer SRF, incluindo unnest:
WITH T1 AS ( SELECT * FROM unnest('{1,2,3,4}'::integer[]) WITH ORDINALITY T(v1, rn) ) , T2 AS ( SELECT * FROM unnest('{5,6}'::integer[]) WITH ORDINALITY T(v2, rn) ) SELECT T1.v1 , T2.v2 FROM T1 LEFT JOIN T2 USING(rn);
 [veja em explicar.tensor.ru]
[veja em explicar.tensor.ru] .
Assim, nos livramos completamente do uso das funções da janela.
UNNEST com vários argumentos
Mas, do ponto de vista da eficiência, nem tudo é bom até agora - quase metade do tempo foi para o Hash Left Join.
E o autor claramente partiu da suposição de que a primeira matriz é exatamente mais longa - é por isso que ele usou LEFT JOIN. Mas essa suposição nem sempre é correta e pode causar problemas.
Para contornar isso, usaremos
unnest para várias matrizes ao mesmo tempo , que apareceram na mesma versão 9.4:
SELECT * FROM unnest( '{1,2,3,4}'::integer[] , '{5,6}'::integer[] ) T(v1, v2);
Como resultado, quase nada restou da solicitação e do plano:
Function Scan on t (cost=0.01..1.00 rows=100 width=8) (actual time=0.006..0.007 rows=4 loops=1)
Portanto, as chances de cometer um erro são muito menores. Sim, e o tempo de execução foi aprimorado várias vezes - e em matrizes mais longas o efeito será ainda mais perceptível.