Matemática genérica não segura em C #

Infelizmente, não foi fácil traduzir adequadamente o nome da feiúra que comecei para o russo. Fiquei surpreso ao descobrir que a documentação oficial do MSDN chama “modelos genéricos” (modelos similares ao C++ , suponho). Na 4ª edição do "CLR via C# ” que chamou minha atenção , Jeffrey Richter , traduzido por Peter , os genéricos são chamados de “generalizações”, o que reflete o conceito muito melhor. Este artigo abordará operações matemáticas generalizadas inseguras em C# . Considerando que o C# não se destina à computação de alto desempenho (embora, é claro, seja capaz disso, mas não seja capaz de competir com o mesmo C/C++ ), as operações matemáticas no BCL não recebem muita atenção. Vamos tentar simplificar o trabalho com tipos aritméticos básicos usando C# e CLR .

Declaração do problema

Isenção de responsabilidade : o artigo conterá muitos fragmentos de código, alguns dos quais ilustrarei com links para o maravilhoso recurso SharpLab ( Gi r tHub ) de Andrey Shchekin .

A maioria dos cálculos, de uma maneira ou de outra, se resume a operações básicas. Adição, subtração (inversão, negação), multiplicação e divisão podem ser complementadas por operações de comparação e verificação de igualdade. Obviamente, todas essas ações podem ser executadas de maneira fácil e simples em variáveis ​​de qualquer tipo aritmético básico de C# . O único problema é que o C# deve saber em tempo de compilação que as operações são executadas em tipos específicos e parece que é impossível escrever um método que igualmente eficiente (e transparente) adicione dois números inteiros e dois números de ponto flutuante.

Vamos especificar nossos desejos por um método generalizado hipotético que execute alguma operação matemática simples:

1. Um método deve ter restrições de tipo generalizadas que nos protegem de tentar adicionar (ou multiplicar, dividir) dois tipos arbitrários. Precisamos de alguma restrição de tipo genérico.
2. Para a pureza do experimento, os tipos aceitos e retornados devem ser os mesmos. Por exemplo, um operador binário deve ter uma assinatura no formato (T, T) => T
3. O método deve ser pelo menos parcialmente otimizado. Por exemplo, o boxe onipresente é inaceitável.

E os vizinhos?

Vamos olhar para F# . Eu não sou forte em F# , mas a maioria das restrições de C# é ditada pelas limitações do CLR , o que significa que o F# sofre dos mesmos problemas. Você pode tentar declarar um método de adição generalizada explícita e o método de adição usual e ver o que o sistema de inferência do tipo F# diz:

 let add_gen (x : 'a) (y : 'a) = x + y let add xy = x + y add_gen 5.0 6.0 |> ignore add 5.0 6.0 |> ignore 

Nesse caso, os dois métodos não serão generalizados e o código gerado será idêntico. Dada a rigidez do sistema do tipo F# , em que não há conversões implícitas no formato int -> double , após a primeira chamada desses métodos com parâmetros do tipo double (em termos de C# ), chame métodos com parâmetros de outros tipos (mesmo com uma possível perda de precisão devido à conversão de tipos) mais falhará.

É importante notar que, se você substituir o operador + operador de igualdade = , a imagem se tornará um pouco diferente : ambos os métodos se tornam generalizados (do ponto de vista de C# ), e um método auxiliar especial, disponível em F# é chamado para realizar a comparação.

 let eq_gen (x : 'a) (y : 'a) = x = y let eq xy = x = y eq_gen 5.0 6.0 |> ignore eq_gen 5 6 |> ignore eq 5.0 6.0 |> ignore eq 5 6 |> ignore 

E o Java ?

É difícil para mim falar sobre Java , mas, tanto quanto posso dizer, tipos significativos não existem da forma usual para nós, mas ainda existem tipos primitivos . Para trabalhar com primitivas em Java existem wrappers (por exemplo, uma referência Long para primitivo por valor long ), que possuem uma classe base comum Number . Portanto, você pode generalizar parcialmente as operações usando Number , mas esse é um tipo de referência, que provavelmente não terá um efeito positivo no desempenho.

Me corrija se eu estiver errado.

C++ ?

C++ é uma linguagem para trapaceiros.
C++ abre caminho para recursos que alguns consideram ... não naturais .
Modelos (também conhecidos como modelos), em contraste com generalizações (genéricos), são, no sentido literal, modelos . Ao declarar um modelo, você pode restringir explicitamente os tipos para os quais esse modelo está disponível. Por esse motivo, em C++ , por exemplo, o seguinte código é válido:

 #include <iostream> template<typename T, std::enable_if_t<std::is_arithmetic<T>::value>* = nullptr> T Add (T left, T right) { return left + right; } int main() { std::cout << Add(5, 6) << std::endl; std::cout << Add(5.0, 6.0) << std::endl; // std::cout << Add("a", "b") << std::endl; Does not compile } 

is_arithmetic , infelizmente, permite char e bool como parâmetros. Por outro lado, char pode ser equivalente a sbyte na terminologia C# , embora os tamanhos reais dos tipos inteiros dependam da fase da plataforma / compilador / lua.

Idiomas de digitação dinâmica

Por fim, considere algumas linguagens dinamicamente tipadas (e interpretadas ), aguçadas pelo cálculo. Nessas linguagens, geralmente a generalização da computação não causa problemas: se o tipo de parâmetro for adequado para execução, além disso, condicionalmente, a operação será executada, caso contrário, falhará com um erro.

No Python (3.7.3 x64):

 def add (x, y): return x + y type(add(5, 6)) # <class 'int'> type(add(5.0, 6.0)) # <class 'float'> type(add('a', 'b') # <class 'str'> 

Em R (3.6.1 x64)

 add <- function(x, y) x + y # Or typeof() vctrs::vec_ptype_show(add(5, 6)) # Prototype: double vctrs::vec_ptype_show(add(5L, 6L)) # Prototype: integer vctrs::vec_ptype_show(add("5", "6")) # Error in x + y : non-numeric argument to binary operator 

Por outro lado, no mundo C #: restringimos o tipo generalizado de função matemática

Infelizmente, não podemos fazer isso. Em C# tipos primitivos são tipos de valor, ou seja, estruturas que, embora herdadas de System.Object (e System.ValueType ), não têm muito em comum. Uma limitação natural e lógica é where T : struct . Começando com C# 7.3 temos a restrição where T : unmanaged , o que significa que T é um , null . Além dos tipos aritméticos primitivos de que precisamos, char , bool , decimal , qualquer Enum e qualquer estrutura cujos todos os campos tenham o mesmo tipo unmanaged atendem a esses requisitos. I.e. este tipo passará no teste:

 public struct Coords<T> where T : unmanaged { public TX; public TY; } 

Portanto, não podemos escrever uma função generalizada que aceite apenas os tipos aritméticos desejados. Daí a Unsafe no título do artigo - teremos que confiar nos programadores que usam nosso código. Uma tentativa de chamar o método hipotético generalizado T Add<T>(T left, T right) where T : unmanaged levará a resultados imprevisíveis se o programador passar objetos de um tipo incompatível como argumentos.

O primeiro experimento, ingênuo: dynamic

dynamic é a primeira e óbvia ferramenta que pode nos ajudar a resolver nosso problema. Obviamente, usar a dynamic para cálculos é absolutamente inútil - a dynamic equivalente ao object , e os métodos chamados com uma variável dynamic são transformados em uma reflexão monstruosa pelo compilador. Como um bônus - empacotar / descompactar nossos tipos de valor. Aqui está um exemplo :

 public class Class { public static void Method() { var x = Add(5, 6); var y = Add(5.0, 6.0); } private static dynamic Add(dynamic left, dynamic right) => left + right; } 

Basta olhar para a IL método Method :

 .method public hidebysig static void Method () cil managed { // Method begins at RVA 0x2050 // Code size 53 (0x35) .maxstack 8 IL_0000: ldc.i4.5 IL_0001: box [System.Private.CoreLib]System.Int32 IL_0006: ldc.i4.6 IL_0007: box [System.Private.CoreLib]System.Int32 IL_000c: call object Class::Add(object, object) IL_0011: pop IL_0012: ldc.r8 5 IL_001b: box [System.Private.CoreLib]System.Double IL_0020: ldc.r8 6 IL_0029: box [System.Private.CoreLib]System.Double IL_002e: call object Class::Add(object, object) IL_0033: pop IL_0034: ret } // end of method Class::Method 

Carregou 5 , empacotou , carregou 6 , empacotou, chamado object Add(object, object) .
A opção obviamente não nos convém.

O segundo experimento, "na testa"

Bem, a dynamic não é para nós, mas o número de nossos tipos é finito e eles são conhecidos antecipadamente. Vamos nos armar com um pé de cabra de ramo e anotá-lo: se nosso tipo for , vamos calcular algo, caso contrário - aqui está a exceção.

 public static T Add<T>(T left, T right) where T : unmanaged { if(left is int i32Left && right is int i32Right) { // ??? } // ... throw new NotSupportedException(); } 

III, aqui nos deparamos com um problema. Se você entender com quais tipos estamos trabalhando, ainda poderá aplicar a operação a eles, então o int condicional resultante precisará ser convertido em um tipo desconhecido T e isso não é muito simples. A opção de return (T)(i32Left + i32Right) não é compilada - não há garantia de que T seja int (mesmo sabendo que é). Você pode tentar o return (T)(object)(i32Left + i32Right) conversão dupla return (T)(object)(i32Left + i32Right) . Primeiro, a quantidade é embalada e depois descompactada em T Isso só funcionará se os tipos corresponderem antes e depois da embalagem. Você não pode empacotar int , mas descompacte-o em double , mesmo se houver uma conversão implícita int -> double . O problema com esse código é a ramificação gigante e a abundância de pacotes de descompactação, mesmo que if condições. Esta opção também não é boa.

Reflexão e Metadados

Bem, toque e basta. Todo mundo sabe que existem operadores em C# que podem ser substituídos. Lá, existem + , - , == , == != E assim por diante. Tudo o que precisamos fazer é usar um método estático do tipo T correspondente ao operador, por exemplo, adições - isso é tudo. Bem, sim, novamente alguns pacotes, mas sem ramificação e sem problemas. A coisa toda pode ser armazenada em cache pelo tipo T e geralmente acelera o processo de todas as formas, reduzindo uma operação matemática a chamar um único método de reflexão. Bem, algo como isto:

 public static T Add<T>(T left, T right) where T : unmanaged { // Simple example without cache. var method = typeof(T) .GetMethod(@"op_Addition", new [] {typeof(T), typeof(T)}) ?.CreateDelegate(typeof(Func<T, T, T>)) as Func<T, T, T>; return method?.Invoke(left, right) ?? throw new InvalidOperationException(); } 

Infelizmente isso não funciona . O fato é que os tipos aritméticos (mas não decimal ) não possuem um método estático. Todas as operações são implementadas através de operações de IL , como add . A reflexão normal não resolve o nosso problema.

System.Linq.Expressions

A solução baseada em Expressions é descrita no blog de John Skeet aqui (de Marc Gravell).
A ideia é bem simples. Suponha que temos um tipo T que suporta a operação + . Vamos criar uma expressão como esta:

 (x, y) => x + y; 

Depois disso, após o cache, vamos usá-lo. Construir essa expressão é bastante fácil. Precisamos de dois parâmetros e uma operação. Então, vamos anotá-la.

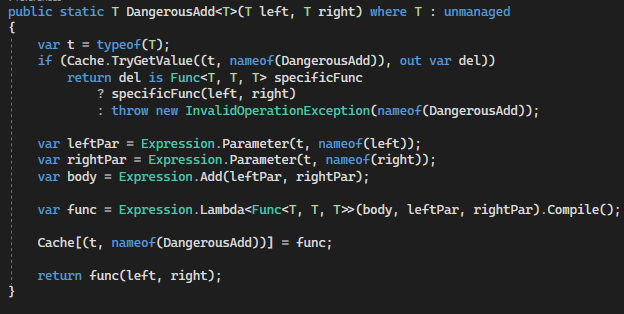
 private static readonly Dictionary<(Type Type, string Op), Delegate> Cache = new Dictionary<(Type Type, string Op), Delegate>(); public static T Add<T>(T left, T right) where T : unmanaged { var t = typeof(T); // If op is cached by type and function name, use cached version if (Cache.TryGetValue((t, nameof(Add)), out var del)) return del is Func<T, T, T> specificFunc ? specificFunc(left, right) : throw new InvalidOperationException(nameof(Add)); var leftPar = Expression.Parameter(t, nameof(left)); var rightPar = Expression.Parameter(t, nameof(right)); var body = Expression.Add(leftPar, rightPar); var func = Expression.Lambda<Func<T, T, T>>(body, leftPar, rightPar).Compile(); Cache[(t, nameof(Add))] = func; return func(left, right); } 

Informações úteis sobre árvores de expressão e delegados foram publicadas no hub

Tecnicamente, expressões nos permitem resolver todos os nossos problemas - qualquer operação básica pode ser reduzida a chamar um método generalizado. Qualquer operação mais complexa pode ser escrita da mesma maneira, usando expressões mais complexas. Isso é quase o suficiente.

Nós quebramos todas as regras

É possível conseguir algo mais usando o poder do CLR/C# ? Vamos ver em que ano o código é gerado por métodos de adição para diferentes tipos :

 public class Class { public static double Add(double x, double y) => x + y; public static int Add(int x, int y) => x + y; // Decimal only to show difference public static decimal Add(decimal x, decimal y) => x + y; } 

O código IL correspondente contém o mesmo conjunto de instruções:

 ldarg.0 ldarg.1 add ret 

Este é o código op muito add no qual a adição de tipos primitivos aritméticos é compilada. decimal nesse local chama static decimal decimal.op_Addition(decimal, decimal) . Mas e se escrevermos um método que será generalizado, mas conter exatamente esse código IL ? Bem, John Skeet adverte que isso não vale a pena . No seu caso, ele considera todos os tipos (incluindo decimal ), bem como seus análogos nullable . Isso exigirá operações de IL não triviais e levará necessariamente a um erro. Mas ainda podemos tentar implementar operações básicas.

Para minha surpresa, o Visual Studio não contém modelos para projetos e arquivos de IL . Você não pode simplesmente pegar e descrever parte do código em IL e incluí-lo em sua montagem. Naturalmente, o código aberto vem em nosso auxílio. O projeto ILSupport contém modelos para projetos de IL , bem como um conjunto de instruções que podem ser adicionadas a *.csproj para incluir o código de IL no projeto. Obviamente, descrever tudo em IL é bastante difícil, portanto o autor do projeto usa o atributo MethodImpl com o sinalizador ForwardRef . Este atributo permite que você declare o método como extern e não descreva o corpo do método. Parece algo como isto:

 [MethodImpl(MethodImplOptions.ForwardRef)] public static extern T Add<T>(T left, T right) where T : unmanaged; 

A próxima etapa é escrever a implementação do método no arquivo *.il com código IL :

 .method public static hidebysig !!T Add<valuetype .ctor (class [mscorlib]System.ValueType modreq ([mscorlib]System.Runtime.InteropServices.UnmanagedType)) T>(!!T left, !!T right) cil managed { .param type [1] .custom instance void System.Runtime.CompilerServices.IsUnmanagedAttribute::.ctor() = (01 00 00 00 ) ldarg.0 ldarg.1 add ret } 

Em nenhum lugar explicitamente referindo-se ao tipo !!T , sugerimos que o CLR adicione dois argumentos e retorne o resultado. Não há verificação de tipo e tudo está na consciência do desenvolvedor. Surpreendentemente, ele funciona e relativamente rápido.

Um pouco de referência

Provavelmente, um benchmark honesto seria construído sobre uma expressão bastante complexa, cujo cálculo seria "frontal", comparado com esses perigosos métodos de IL . Escrevi um algoritmo simples que resume os quadrados de números previamente calculados e armazenados em uma matriz double e divide o valor final pelo número de números. Para executar a operação, usei os operadores C# + , * e / , como fazem as pessoas saudáveis, funções criadas com Expressions e IL .

 BenchmarkDotNet=v0.12.0, OS=Windows 10.0.18362 Intel Core i7-2700K CPU 3.50GHz (Sandy Bridge), 1 CPU, 8 logical and 4 physical cores .NET Core SDK=3.1.100 [Host] : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Job-POXTAH : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Runtime=.NET Core 3.1 

Nosso código inseguro é cerca de 2.5 vezes mais lento (em termos de uma operação). Isso pode ser atribuído ao fato de que, no caso de um cálculo de "testa", o compilador compila a + b no código de operação add e, no caso de um método inseguro, é chamada uma função estática, que é naturalmente mais lenta.

Em vez de concluir: quando true != true

Alguns dias atrás, me deparei com um tweet de Jared Parsons:

Há casos em que o seguinte imprimirá "false"
bool b = ...
if (b) Console.WriteLine (b.IsTrue ());

Esta foi a resposta para esta entrada , que mostra o código de verificação bool para true , que se parece com isso:

 public static bool IsTrue(this bool b) { if (b == true) return true; else if (b == false) return false; else return !true && !false; } 

Os cheques parecem redundantes, certo? Jared fornece um contra-exemplo que demonstra alguns dos recursos do comportamento bool . A idéia é que bool seja byte ( sizeof(bool) == 1 ), enquanto false corresponde a 0 e true corresponde a 1 . Contanto que você não gire os ponteiros, o bool se comporta de maneira inequívoca e previsível. No entanto, como Jared mostrou, você pode criar um bool usando 2 como valor inicial e algumas das verificações falharão corretamente:

 bool b = false; byte* ptr = (byte*)&b; *ptr = 2; 

Podemos obter um efeito semelhante usando nossas operações matemáticas inseguras (isso não funciona com Expressions ):

 var fakeTrue = Subtract<bool>(false, true); var val = *(byte*)&fakeTrue; if(fakeTrue) Assert.AreNotEqual(fakeTrue, true); else Assert.Fail("Clause not entered."); 

Sim, sim, verificamos dentro do ramo true se a condição é true e esperamos que, de fato, não seja true . Por que isso é assim? Se você subtrair de 0 ( =false ) 1 ( =true ) sem verificações, o byte será igual a 255 . Naturalmente, 255 (nosso fakeTrue ) não é 1 (verdadeiro true ), portanto, a afirmação é executada. A ramificação funciona de maneira diferente.

if ocorrer inversão: um ramo condicional é inserido; se a condição for falsa , ocorrerá uma transição para o ponto após o final do bloco if . A validação é realizada pela brfalse_S / brfalse_S . Ele compara o último valor na pilha com zero . Se o valor é zero, então é false , passamos o bloco if . No nosso caso, fakeTrue simplesmente não é igual a zero, portanto a verificação passa e a execução continua dentro do bloco if , onde comparamos fakeBool com o valor true e obtemos um resultado negativo.

UPD01:
Depois de discutir nos comentários com shai_hulud e blowin , adicionei outro método aos benchmarks que implementam um ramo como if(typeof(T) == typeof(int)) return (T)(object)((int)(object)left + (int)(object)right); . Apesar do JIT otimizar as verificações, pelo menos quando T é uma struct , esses métodos ainda funcionam em uma ordem de magnitude mais lenta. Não é óbvio se as transformações T -> int -> T otimizadas ou se o boxe / unboxing é usado. Os resultados do benchmark MethodImpl são significativamente afetados pelos sinalizadores MethodImpl .

UPD02:
O xXxVano nos comentários mostrou um exemplo de uso de ramificação por tipo e lança T <--> um tipo específico usando Unsafe.As<TFrom, TTo>() . Por analogia com a ramificação usual e o costume através do object , escrevi três operações (adição, multiplicação e divisão) com ramificação para todos os tipos aritméticos, após as quais adicionei outro benchmark ( UnsafeBranchSum ). Apesar do fato de que todos os métodos (exceto expressões) geram código asm quase idêntico (até onde meu conhecimento limitado de assembler me permite julgar), por algum motivo desconhecido, ambos os métodos com ramificação são muito lentos em comparação com a soma direta ( DirectSum ) e usando genéricos e código IL . Não tenho explicação para esse efeito, o fato de o tempo gasto aumentar na proporção de N indica que há algum tipo de sobrecarga constante para cada operação, apesar de toda a magia do JIT . Essa sobrecarga está ausente na versão IL dos métodos. , IL - , / / , 100% ( , ).
, , - .