Boa tarde
Neste artigo, tentarei dar uma nova olhada no algoritmo para encontrar uma solução geral para um sistema de equações lineares.
A tarefa que faremos é a seguinte.
Encontre uma solução geral para o seguinte sistema de equações
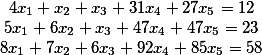
Esse problema é resolvido reduzindo o sistema inicial para uma forma triangular, de acordo com o método de Gauss. Então, escolhendo variáveis livres, a solução geral é calculada.
Quero mostrar como alguém pode resolver esses sistemas de outra maneira. Tanto quanto é conhecido e aplicado em outros lugares, não consegui descobrir. Em todos os materiais públicos / populares, o método Gauss é usado.
Devo dizer imediatamente que a solução certamente não é ótima (em termos de velocidade), pois ao calcular um produto vetorial, é necessário calcular o determinante da matriz, e este é de alguma forma o cálculo da matriz triangular.
Mas a solução é bonita e clara, além disso, é fácil ver o critério sob o qual o sistema não tem soluções.
Qual é a essência da técnica?
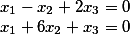
Resolvendo este sistema como produto de dois vetores, obtemos
i%20+%20(%201%20)j%20+%20(%207%20)k)
Portanto, as raízes do sistema são iguais
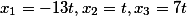
Para quem não acredita, isso é facilmente verificado por substituição.
Usamos essa técnica e consideramos como esses sistemas são resolvidos usando produtos vetoriais.
Então nós temos o sistema de origem
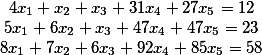
Mova os termos gratuitos para o lado esquerdo
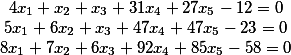
Temos 6 colunas.
Nesta fase, não apresentaremos novas entidades e não usaremos os conceitos de classificação matricial em nosso trabalho. (Por favor, trate-me com condescendência)
Vemos apenas que existem 3 equações e 5 variáveis. Portanto, a solução geral usará 5-3 = 2 variáveis independentes.
Na mesma etapa, podemos determinar quais das variáveis estarão livres. Pegamos duas variáveis que estarão à direita de todos e as libertamos.
Nota: Para outras equações, nem sempre é necessário tomar apenas os últimos coeficientes corretos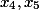
E agora, em três etapas, determinamos a solução fundamental do sistema original
Etapa 1. Aqui a última coluna são os membros livres do sistema.
i%20+%20(%20-162%20)j%20+%20(%20-486%20)k%20+%20(%20-81%20)l)
Etapa 2. Aqui a última coluna é os coeficientes para a variável
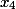
i%20+%20(%20162%20)j%20+%20(%20405%20)k%20+%20(%20-81%20)l)
Etapa 3. Aqui a última coluna é os coeficientes para a variável
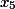
i%20+%20(%20243%20)j%20+%20(%20324%20)k%20+%20(%20-81%20)l)
Não há necessidade de informar em detalhes de onde obtemos os dados. Eu acho que isso é óbvio para os leitores. (Quem resolveu o sistema de equações usando o método Cramer encontrará características comuns)
O que é mais interessante é o que faremos com esses "vetores".
Divida-os por -81
temos os seguintes três vetores
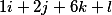
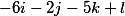
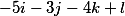
organizá-los verticalmente e, portanto, a decisão fundamental assume a forma
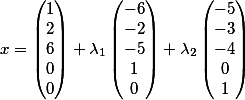
Ótimo! Não é ...
Para o critério de solvabilidade de um determinado sistema de equações, na maioria dos casos é usada a regra de Kronecker-Copelli, aqui o resultado do produto vetorial é simplesmente analisado.
Se o vetor resultante tiver a forma
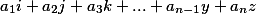
onde 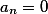 , e entre todos os restantes, há pelo menos um diferente de zero, então esse sistema de soluções não temSe o vetor resultante tiver todos os coeficientes zero, isso indica que pelo menos uma das equações é uma representação linear da outra e / ou uma das variáveis é proporcional à outra.
, e entre todos os restantes, há pelo menos um diferente de zero, então esse sistema de soluções não temSe o vetor resultante tiver todos os coeficientes zero, isso indica que pelo menos uma das equações é uma representação linear da outra e / ou uma das variáveis é proporcional à outra.Este artigo é o primeiro, e eu gostaria de ouvir comentários, críticas, desejos em meu endereço.
O algoritmo e a calculadora foram
criados em janeiro de 2019 e só hoje decidi publicar informações sobre Habré.
Se você aceitar em sua equipe / sociedade, o próximo tópico será
- Como encontrar uma solução geral para o sistema de equações diofantinas.