
Computadores quânticos e computação quântica são uma nova palavra de ordem que foi adicionada ao nosso espaço de informações, juntamente com inteligência artificial , aprendizado de máquina e outros termos de alta tecnologia. Ao mesmo tempo, não consegui encontrar material na Internet que colocasse na minha cabeça um quebra-cabeça chamado "como os computadores quânticos funcionam" . Sim, existem muitos trabalhos excelentes, inclusive no Habré (veja a Lista de recursos ), os comentários nos quais, como costuma acontecer, são ainda mais informativos e úteis, mas a imagem na cabeça, como se costuma dizer, não se encaixou.
Recentemente, colegas me procuraram e perguntaram: “Você entende como funciona um computador quântico? Você pode nos contar? ”E então eu percebi que o problema de dobrar uma imagem completa na minha cabeça não é apenas meu.
Como resultado, foi feita uma tentativa de compilar informações sobre computadores quânticos em um esquema lógico consistente no qual, em um nível básico, sem imersão profunda na matemática e na estrutura do mundo quântico , foi explicado o que era um computador quântico, quais princípios ele trabalhava e também quais problemas enfrentavam. cientistas em sua criação e operação.
Sumário
Isenção de responsabilidade
(ao conteúdo)
O autor não é especialista em computação quântica, e o público-alvo do artigo são os mesmos especialistas em TI, não especialistas em quantum , que também desejam montar uma imagem chamada "Como os computadores quânticos funcionam". Por esse motivo, muitos conceitos no artigo são deliberadamente simplificados para uma melhor compreensão das tecnologias quânticas no nível "básico", mas sem muita simplificação com a perda de conteúdo e adequação das informações .
Em alguns lugares, o artigo usa materiais de outras fontes, cuja lista é fornecida no final do artigo . Sempre que possível, são inseridos links diretos e referências ao texto, tabela ou imagem original. Se em algum lugar eu esqueci algo (ou alguém), escreva - eu o corrigirei.
1. Introdução
(ao conteúdo)
Neste capítulo, examinaremos brevemente como começou a era quântica, que foi a motivação para a idéia de um computador quântico, quem (quais países e empresas) são atualmente os principais participantes desta clareira e falaremos brevemente sobre as principais direções de desenvolvimento da computação quântica.
Como tudo começou
(ao conteúdo)

O ponto de partida da era quântica é considerado o ano de 1900, quando M. Planck apresentou pela primeira vez a hipótese de que a energia é emitida e absorvida não continuamente, mas em quanta (porções) separadas. A idéia foi escolhida e desenvolvida por muitos cientistas destacados da época - Bohr, Einstein, Heisenberg, Schrödinger, que, em última análise, levaram à criação e desenvolvimento de uma ciência como a física quântica . Existem muitos materiais bons sobre o desenvolvimento da física quântica como ciência na Web. Neste artigo, não iremos nos aprofundar nisso em detalhes, mas era necessário indicar a data em que entramos na nova era quântica.
A física quântica trouxe para a vida cotidiana muitas invenções e tecnologias, sem as quais agora é difícil imaginar o mundo ao nosso redor. Por exemplo, um laser que agora é usado em qualquer lugar, de eletrodomésticos (níveis de laser, etc.) a sistemas de alta tecnologia (lasers de correção da visão, olá meklon ). Seria lógico supor que, mais cedo ou mais tarde, alguém apresentará a ideia de por que não usar sistemas quânticos para cálculos. E assim, em 1980, aconteceu.
A Wikipedia indica que o cientista Yuri Manin foi o primeiro a expressar a idéia da computação quântica em 1980. Mas eles realmente começaram a falar sobre isso apenas em 1981, quando o conhecido R. Feynman, em seu relatório na primeira conferência sobre física computacional realizada no Instituto de Tecnologia de Massachusetts , observou que é impossível modelar a evolução de um sistema quântico em um computador clássico de maneira eficaz. Ele propôs um modelo elementar de um computador quântico que seria capaz de realizar tal simulação.
Existe um trabalho na Web em que a cronologia do desenvolvimento da computação quântica é considerada mais academicamente e em detalhes, mas examinaremos brevemente:
Marcos na história dos computadores quânticos:
Como você pode ver, 17 anos se passaram (de 1981 a 1998) desde o momento da ideia até sua primeira implementação em um computador com 2 qubits e 21 anos (de 1998 a 2019) até o momento em que o número de qubits aumentou para 53. Foram necessários 11 anos (de 2001 a 2012) para melhorar o resultado do algoritmo Shore (vamos nos aprofundar um pouco mais) do número 15 para 21. Além disso, apenas três anos atrás, descobrimos o que Feynman falou e Aprenda a simular os sistemas físicos mais simples.
O desenvolvimento da computação quântica é lento. Cientistas e engenheiros enfrentam tarefas muito complexas, os estados quânticos têm vida curta e frágil, e para mantê-los por tempo suficiente para realizar cálculos, é preciso construir sarcófagos por dezenas de milhões de dólares, nos quais a temperatura é mantida logo acima do zero absoluto e protegida contra influências externas. Além disso, falaremos sobre essas tarefas e problemas com mais detalhes.
Jogadores líderes
(ao conteúdo)

Os slides desta seção foram retirados do artigo Quantum Computer: A Big Boost Game. Palestra em Yandex , de um pesquisador do Centro Quântico Russo Alexei Fedorov. Permitirei-me citações diretas:
Todos os países tecnologicamente bem-sucedidos estão atualmente envolvidos ativamente no desenvolvimento de tecnologias quânticas. Uma quantidade enorme de dinheiro é investida nesses estudos; programas especiais para apoiar tecnologias quânticas estão sendo criados.

A corrida quântica envolve não apenas estados, mas também empresas privadas. No total, Google, IBM, Intel e Microsoft investiram cerca de US $ 0,5 bilhão no desenvolvimento de computadores quânticos nos últimos anos, criaram grandes laboratórios e centros de pesquisa.
Existem muitos artigos sobre Habré e na Web, por exemplo, aqui , aqui e aqui , nos quais o estado atual das coisas com o desenvolvimento de tecnologias quânticas em diferentes países é considerado com mais detalhes. Para nós agora, o principal é que todos os principais países e players tecnologicamente desenvolvidos invistam grandes quantias de dinheiro em pesquisas nessa direção, o que dá esperança de uma saída do atual impasse tecnológico.
Instruções de desenvolvimento
(ao conteúdo)

No momento (posso estar errado, correto), os principais esforços (e resultados mais ou menos significativos) para todos os principais jogadores estão concentrados em duas direções:
- Computadores quânticos especializados que visam solucionar um problema específico específico, por exemplo, problemas de otimização. Um exemplo de produto são os computadores quânticos D-Wave.
- Computadores quânticos universais - capazes de implementar algoritmos quânticos arbitrários (Shore, Grover, etc.). Implementações da IBM, Google.
Outros vetores de desenvolvimento que a física quântica nos fornece, como:
certamente também na lista de áreas para pesquisa, mas algum tipo de resultado mais ou menos significativo atualmente parece estar lá.
Além disso, você pode ler o roteiro para o desenvolvimento de tecnologias quânticas , bem, no Google " desenvolvimento de tecnologias quânticas ", por exemplo, aqui , aqui e aqui .
O básico. Objetos quânticos e sistemas quânticos
(ao conteúdo)

A coisa mais importante a entender nesta seção é que
Um computador quântico (em contraste com o convencional) usa objetos quânticos como portadores de informações, e os objetos quânticos devem ser conectados a um sistema quântico para realizar cálculos.
O que é um objeto quântico?
Um objeto quântico é um objeto do microworld (mundo quântico) que exibe propriedades quânticas:
- Tem um certo estado com dois níveis de limite
- Está em uma superposição de seu estado até o momento da medição
- Emaranhado com outros objetos para criar sistemas quânticos
- Executa um teorema de proibição de clone (você não pode copiar o estado de um objeto)
Vamos analisar cada propriedade em mais detalhes:
Tem um determinado estado com dois níveis de limite (estado final)
Um exemplo clássico do mundo real é uma moeda. Ela tem um estado de "lado", que leva dois níveis de fronteira - "águia" e "caudas".
Está em uma superposição de seu estado até o momento da medição
Jogou uma moeda, voa e gira. Enquanto está girando, é impossível dizer em qual dos níveis de fronteira seu estado “lateral” está localizado. Mas, se o criticarmos e olharmos para o resultado, a superposição de estados se desintegra imediatamente em um dos dois limites - “cara” e “coroa”. Bater uma moeda no nosso caso é uma dimensão.
Emaranhado com outros objetos para criar sistemas quânticos
É difícil com uma moeda, mas vamos tentar. Imagine que jogamos três moedas para que elas girem agarradas uma à outra, como um malabarismo de moedas. A cada momento, não apenas cada um deles se sobrepõe a estados, mas esses estados se influenciam mutuamente (as moedas colidem).
Executa um teorema de proibição de clone (você não pode copiar o estado de um objeto)
Enquanto as moedas estão girando e girando, não podemos de forma alguma criar uma cópia do estado de rotação de qualquer uma das moedas separadas do sistema. O sistema vive em si mesmo e tem muita inveja de fornecer qualquer informação.
Algumas palavras sobre o próprio conceito de “superposição” , em quase todos os artigos, a superposição é explicada como “está em todos os estados ao mesmo tempo”, o que, é claro, é verdade, mas às vezes é muito confuso. Uma superposição de estados também pode ser pensada como o fato de que, a todo momento, um objeto quântico tem certas probabilidades de colapsar em cada um de seus níveis de fronteira, e no total essas probabilidades são naturalmente iguais a 1 . Além disso, ao considerar o qubit, vamos nos aprofundar nisso com mais detalhes.
Para moedas, isso pode ser imaginado visualmente - dependendo da velocidade inicial, do ângulo do lançamento, do estado do ambiente em que a moeda voa, a cada momento, a probabilidade de obter uma “águia” ou “coroa” é diferente. E, como mencionado anteriormente, o estado de uma moeda voadora pode ser imaginado como "está em todos os seus estados de fronteira ao mesmo tempo, mas com uma probabilidade diferente de sua implementação".
Qualquer objeto para o qual as propriedades acima sejam satisfeitas e que possamos criar e gerenciar pode ser usado como um meio de armazenamento em um computador quântico.
Um pouco mais adiante, falaremos sobre o estado atual das coisas com a implementação física de qubits como objetos quânticos e o que os cientistas estão usando agora nessa capacidade.
Portanto, a terceira propriedade diz que objetos quânticos podem ser enredados para criar sistemas quânticos. O que é um sistema quântico?
Um sistema quântico é um sistema de objetos quânticos emaranhados com as seguintes propriedades:
- Um sistema quântico está em uma superposição de todos os estados possíveis dos objetos dos quais consiste
- É impossível conhecer o estado do sistema até o momento da medição
- No momento da medição, o sistema implementa uma das possíveis variantes de seus estados de contorno
(e correndo um pouco à frente)
Corolário de programas quânticos :
- Um programa quântico possui um dado estado do sistema na entrada, uma superposição interna, uma superposição na saída
- Na saída do programa após a medição, temos uma implementação probabilística de um dos possíveis estados finais do sistema (mais possíveis erros)
- Qualquer programa quântico possui uma arquitetura de chaminé (entrada -> saída. Não há ciclos, você não pode ver o estado do sistema no meio do processo).
Comparação de um computador quântico e um computador convencional
(ao conteúdo)

Vamos agora comparar um computador convencional com um computador quântico.
Nível lógico

Em um computador comum, isso é um pouco. Um pouco determinístico bem conhecido. Ele pode assumir os valores 0 ou 1. Ele lida com o papel de uma unidade lógica para um computador comum, mas é completamente inadequado para descrever o estado de um objeto quântico , que, como já dissemos, está em estado selvagem com a suposição de seus estados de fronteira .
Para isso, um qubit foi inventado. Em seus estados de contorno, ele realiza os estados | 0> e | 1> semelhantes a 0 e 1 e, em superposição, representa uma distribuição de probabilidade sobre seus estados de contorno |0> e |1> :
a|0> + b|1>, , a^2+b^2=1
neste caso, a e b representam as amplitudes das probabilidades , e os quadrados de seus módulos representam as probabilidades de fato para obter precisamente esses valores dos estados de contorno |0> e |1>, se o qubit for colapsado por medição no momento.
Nível físico
No atual nível tecnológico de desenvolvimento, a implementação física de um bit para um computador comum é um transistor semicondutor , para um quantum, como dissemos, qualquer objeto quântico . Na próxima seção, falaremos sobre o que agora é usado como portadores físicos de qubits.
Meio de armazenamento
Para um computador comum, trata-se de uma corrente elétrica - níveis de tensão, presença ou ausência de corrente etc., para um quântico - o próprio estado de um objeto quântico (direção da polarização, rotação, etc.), que pode estar em um estado de superposição.
Operações
Para implementar circuitos lógicos em um computador comum, todos usamos operações lógicas conhecidas; para operações em qubits, tivemos que criar um sistema de operações completamente diferente, chamado portas quânticas . Os portões são de um e dois qubit, dependendo de quantos qubits são convertidos.
Exemplos de portões quânticos:
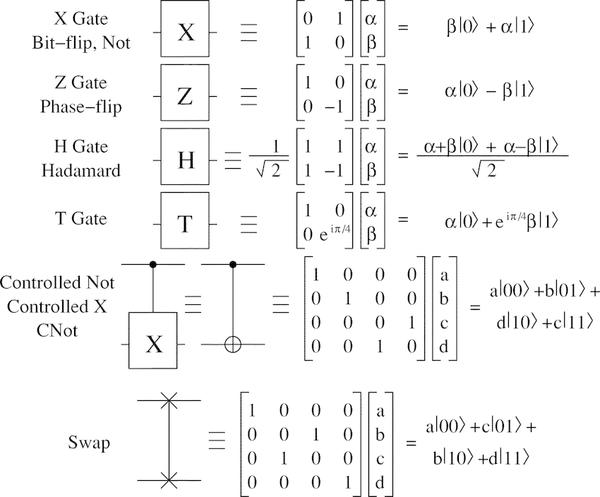
Existe o conceito de um conjunto universal de portas , suficientes para realizar qualquer cálculo quântico. Por exemplo, um conjunto universal inclui uma válvula Hadamard, uma válvula de mudança de fase, uma válvula CNOT e uma válvula π⁄8. Com a ajuda deles, você pode executar qualquer cálculo quântico em um conjunto arbitrário de qubits.
Neste artigo, não falaremos em detalhes sobre o sistema de portas quânticas; em mais detalhes sobre eles, e operações lógicas em qubits podem ser lidas, por exemplo, aqui . A principal coisa a lembrar:
- Operações em objetos quânticos requerem a criação de novos operadores lógicos (portas quânticas)
- As válvulas quânticas são de um e dois qubit
- Existem conjuntos universais de portões com os quais você pode executar qualquer cálculo quântico
Interconexão
Um transistor é completamente inútil para nós; para fazer cálculos, precisamos conectar muitos transistores entre si, ou seja, criar um chip semicondutor a partir de milhões de transistores, nos quais já construímos circuitos lógicos, ALUs e, finalmente, obtemos um processador moderno em sua forma clássica.
Um qubit também é completamente inútil para nós (bem, mesmo que apenas em termos acadêmicos),
para fazer cálculos, precisamos de um sistema de qubits (objetos quânticos)
que, como já dissemos, é criado entrelaçando qubits entre si para que as mudanças em seus estados ocorram em conjunto.
Algoritmos
Os algoritmos padrão que a humanidade acumulou até o momento atual são completamente inadequados para implementação em um computador quântico. Sim, em geral, e não há necessidade. Os computadores quânticos baseados na lógica da porta sobre os qubits requerem a criação de algoritmos completamente diferentes, algoritmos quânticos. Dos algoritmos quânticos mais famosos, três podem ser distinguidos:
Princípio
E a diferença mais importante é o princípio do trabalho. Para um computador padrão, esse é um princípio digital, estritamente determinado , com base no fato de que, se definirmos algum estado inicial do sistema e o passarmos por um determinado algoritmo, o resultado dos cálculos será o mesmo, não importa quantas vezes executemos esse cálculo. Na verdade, esse comportamento é exatamente o que esperamos do computador.
Um computador quântico funciona com um princípio probabilístico analógico . O resultado de um determinado algoritmo em um determinado estado inicial é uma amostra da distribuição de probabilidade das implementações finais do algoritmo, além de possíveis erros.
Essa natureza probabilística da computação quântica se deve à própria essência probabilística do mundo quântico. "Deus não joga dados com o universo ", disse o velho Einstein, mas todos os experimentos e observações até agora (no atual paradigma científico) confirmam o contrário.
Implementações físicas de qubits
(ao conteúdo)

Como já dissemos, um qubit pode ser representado por um objeto quântico, ou seja, um objeto físico que implementa as propriedades quânticas descritas acima. Ou seja, grosso modo, qualquer objeto físico no qual haja dois estados e esses dois estados estejam em um estado de superposição pode ser usado para construir um computador quântico.
“Se podemos colocar um átomo em dois níveis diferentes e controlá-los, então aqui está um qubit para você. Se pudermos fazer isso com um íon, qubit. É o mesmo com a corrente. Se rodarmos no sentido horário e anti-horário ao mesmo tempo, aqui está um qubit. ” (C)
Há um comentário maravilhoso sobre o artigo em que a variedade atual de realizações físicas do qubit é considerada em mais detalhes, mas apenas listamos as mais famosas e comuns:
De toda essa diversidade, o primeiro método para produzir qubits baseados em supercondutores é o mais elaborado. Google , IBM , Intel e outros players líderes usam-no para construir seus sistemas.
Bem, leia também a revisão de possíveis realizações físicas de qubits de Andrew Daley, 2014 .
O básico. O princípio de operação de um computador quântico
(ao conteúdo)

Os materiais para esta seção (tarefa e fotos) foram retirados do artigo “Apenas sobre o complexo. Como um computador quântico funciona . ”
Então, vamos imaginar que temos a seguinte tarefa:
Há um grupo de três pessoas: (A) ndrey, (B) olodya e (C) heresia . Existem dois táxis (0 e 1) .
Sabe-se também que:
- (A) ndrey, (B) olodya - amigos
- (A) ndrey, (C) heresia - inimigos
- (B) olodya e (C) heresia - inimigos
Tarefa: Coloque as pessoas de táxi para que Max (amigos) e Min (inimigos)
Pontuação: L = (número de amigos) - (número de inimigos) para cada opção de acomodação
IMPORTANTE: Assuma que não há heurística, não há solução ideal. Nesse caso, o problema é resolvido apenas pela pesquisa exaustiva de opções.
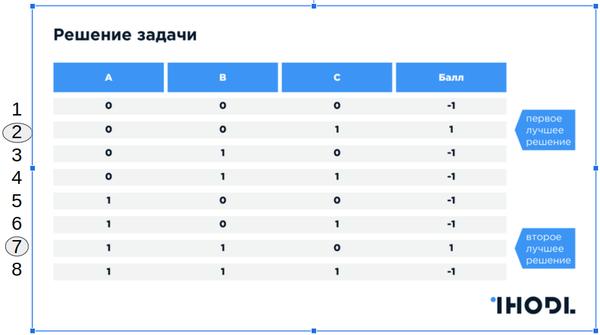
Solução em um computador comum
Como resolver esse problema em um (super) computador (ou cluster) regular - é claro que precisamos classificar todas as opções possíveis em um loop . Se tivermos um sistema multiprocessador, poderemos paralelizar o cálculo de soluções em vários processadores e coletar os resultados.
Temos 2 opções de acomodação possíveis (táxi 0 e táxi 1) e 3 pessoas. O espaço das soluções é 2 ^ 3 = 8 . Você pode percorrer 8 opções, mesmo em uma calculadora, isso não é um problema. E agora vamos complicar a tarefa - temos 20 pessoas e dois barramentos, o espaço da solução é 2 ^ 20 = 1.048.576 . Nada muito complicado. Vamos aumentar o número de pessoas em 2,5 vezes - pegue 50 pessoas e dois trens, o espaço de decisão agora é 2 ^ 50 = 1,12 x 10 ^ 15 . Um (super) computador normal já está começando a ter problemas sérios. Aumentaremos o número de pessoas em 2 vezes, 100 pessoas nos fornecerão 1,2 x 10 ^ 30 opções possíveis.
Tudo, em um tempo razoável, esta tarefa não pode ser contada.
Conectamos um supercomputador
O computador mais poderoso atualmente é o número 1 do Top500 , é o Summit , com capacidade para 122 Pflops . Suponha que, para o cálculo de uma opção, 100 operações sejam suficientes para nós, para resolver o problema para 100 pessoas que precisamos:
(1,2 x 10 ^ 30 100) / 122x10 ^ 15 / (60 60 24 365) = 3 x 10 ^ 37 anos.
Como vemos, à medida que a dimensão dos dados de origem aumenta, o espaço das soluções aumenta de acordo com uma lei de energia ; no caso geral de N bits, temos 2 ^ N soluções possíveis que, com N (100) relativamente pequeno, nos dão um espaço ilegível (no nível tecnológico atual) decisões.
Existem alternativas? Como você deve ter adivinhado, sim, existe.
Mas antes de prosseguirmos sobre como e por que os computadores quânticos podem efetivamente resolver esses problemas, vamos lembrar um pouco sobre o que é uma distribuição de probabilidade . Não se assuste, o artigo de revisão, não haverá matemática difícil aqui, vamos dar um exemplo clássico com uma bolsa e bolas.
Bastante combinação, teoria das probabilidades e um experimentador estranho
Pegue uma bolsa e coloque nela 1000 bolas brancas e 1000 bolas pretas . Realizaremos um experimento - retire a bola, anote a cor, devolva a bola à sacola e misture as bolas na sacola.
Realizamos o experimento 10 vezes, retiramos 10 bolas pretas . Talvez? Bastante. Esta amostra nos fornece um conceito razoável da verdadeira distribuição na bolsa? Obviamente não. O que você precisa fazer é certo, repita o experimento um milhão de vezes e calcule a frequência da queda de bolas pretas e brancas. Temos, por exemplo, 49,95% em preto e 50,05% em branco . Nesse caso, a estrutura de distribuição da qual coletamos amostras já é mais ou menos clara (pegamos uma bola).
O principal que você precisa entender é que o experimento em si é probabilístico por natureza . Com uma amostra (bola) que não reconhecemos a verdadeira estrutura de distribuição, precisamos repetir o experimento várias vezes e calcular a média dos resultados.
Adicione 10 bolas vermelhas e 10 verdes à nossa bolsa (erros). Repita o experimento 10 vezes. Em puxado 5 vermelho e 5 verde . Talvez? Sim Podemos dizer algo sobre a verdadeira distribuição - Não. O que precisa ser feito - bem, você entende.
Para entender melhor a estrutura da distribuição de probabilidade, é necessário amostrar repetidamente os resultados individuais dessa distribuição e calcular a média dos resultados.
Conectamos teoria com prática
Agora, em vez de bolas pretas e brancas, vamos pegar as bolas de bilhar e colocar na bolsa 1000 bolas com o número 2, 1000 com o número 7 e 10 bolas com outros números . Imagine um experimentador treinado em etapas simples (pegue uma bola, anote o número, coloque a bola de volta na sacola, misture as bolas na sacola) e ele faz isso em 150 microssegundos. Bem, um experimentador de Aids (não propaganda de drogas !!!). Então, em 150 segundos, ele poderá realizar nosso experimento 1 milhão de vezes e fornecer os resultados da média.
Eles sentaram o experimentador, deram a bolsa, se afastaram, esperaram 150 segundos - receberam:
número 2 - 49,5%, número 7 - 49,5%, os números restantes no valor - 1%.
Sim, está certo, nossa bolsa é um computador quântico com um algoritmo que resolve nosso problema , e bolas são possíveis soluções. Como existem duas soluções corretas, um computador quântico nos dará a mesma probabilidade de qualquer uma dessas possíveis soluções e erros de 0,5% (10/2000) , sobre os quais falaremos mais adiante.
Para obter o resultado de um computador quântico, você precisa executar o algoritmo quântico repetidamente no mesmo conjunto de dados de entrada e calcular a média do resultado.
Escalabilidade de um computador quântico
Agora vamos imaginar que, para um problema em que 100 pessoas participem (lembramos desse espaço de decisão 2 ^ 100 ), existem apenas duas soluções corretas. Então, se pegarmos 100 qubits e escrevermos um algoritmo que calcula nossa função objetivo (L, veja acima) nesses qubits, obteremos uma sacola que contém 1000 bolas com o número da primeira resposta correta, 1000 com o número da segunda resposta correta e 10 bolas com outros números. E nosso pesquisador nos mesmos 150 segundos nos dará uma estimativa da distribuição probabilística das respostas corretas .
O tempo de execução do algoritmo quântico (com algumas suposições) pode ser considerado constante O (1) em relação à dimensão do espaço da solução (2 ^ N).
E é precisamente essa propriedade de um computador quântico - a chave do tempo de execução no que diz respeito à complexidade do espaço de decisão que cresce de acordo com a lei do poder.
Qubit e mundos paralelos
Como isso acontece? O que permite que um computador quântico faça cálculos tão rapidamente? É tudo sobre a natureza quântica do qubit.
Olha, dissemos que um qubit como objeto quântico realiza um de seus dois estados quando é observado , mas na "natureza viva" está em uma superposição de estados , ou seja, está em ambos os estados de fronteira ao mesmo tempo (com alguma probabilidade).
Tome (A) Ndrey e imagine sua condição (na qual o veículo é 0 ou 1) como um qubit. Então temos (em um espaço quântico) dois mundos paralelos , em um (A) sentado em um táxi 0, em outro mundo - em um táxi 1. Ao mesmo tempo em dois táxis , mas com alguma chance de encontrá-lo em cada um deles ao observar.
Tome (B) olod e também imagine seu estado como um qubit. Dois outros mundos paralelos surgem. Mas enquanto esses pares de mundos (A) e (B) não interagem de forma alguma. O que precisa ser feito para criar um sistema conectado ? É isso mesmo, você precisa conectar (confundir) esses qubits. Tomamos e confundimos (A) com (B) - obtemos um sistema quântico de dois qubits (A, B), que implementa quatro mundos paralelos interdependentes dentro de si. Adicione (C) erge e obtenha um sistema de três qubits (ABC), que implementa oito mundos paralelos interdependentes .
A essência da computação quântica (a implementação de uma cadeia de portas quânticas sobre um sistema de qubits acoplados) é o fato de que o cálculo ocorre em todos os mundos paralelos simultaneamente.
E não importa quantos deles tenhamos, 2 ^ 3 ou 2 ^ 100, o algoritmo quântico será executado em um tempo finito em todos esses mundos paralelos e nos fornecerá o resultado, que é uma amostra da distribuição de probabilidade das respostas do algoritmo.
Para uma melhor compreensão, podemos imaginar que um computador quântico no nível quântico inicie processos de decisão paralelos 2 ^ N , cada um dos quais funciona em uma opção possível, em seguida, colete os resultados do trabalho - e nos dê a resposta na forma de uma superposição da solução (distribuição de probabilidade das respostas), de que amostramos uma vez de cada vez (em cada experimento).
Lembre-se do tempo que o nosso experimentador (150 μs) leva para realizar o experimento; isso será útil um pouco mais quando falarmos sobre os principais problemas dos computadores quânticos e o tempo de decoerência.
Algoritmos quânticos
(ao conteúdo)
Como já mencionado, algoritmos convencionais baseados em lógica binária não são aplicáveis a um computador quântico que usa lógica quântica (portas quânticas). Para ele, ele teve que criar novos que fizessem pleno uso do potencial inerente à natureza quântica da computação.
Os algoritmos mais famosos da atualidade são:
Ao contrário dos clássicos, os computadores quânticos não são universais.
Até agora, apenas um pequeno número de algoritmos quânticos foi encontrado. (C)
Agradecemos a oxoron pelo link para o Zoológico de Algoritmo Quântico , o local onde, de acordo com o autor ( Stephen Jordan ), os melhores representantes do mundo do algoritmo quântico foram reunidos e continuam a se reunir.
Neste artigo, não analisaremos detalhadamente os algoritmos quânticos; existem muitos materiais excelentes na Web para qualquer nível de complexidade, mas você ainda precisa revisar brevemente os três mais famosos.
Algoritmo Shore.
(ao conteúdo)
O algoritmo quântico mais famoso é o algoritmo Shor (inventado em 1994 pelo matemático inglês Peter Shor ), que visa solucionar o problema de decompor números em fatores primos (o problema de fatoração, o logaritmo discreto).
Esse algoritmo é usado como exemplo quando eles escrevem que seus sistemas bancários e senhas serão invadidos em breve. Considerando que o comprimento das chaves usadas hoje não é inferior a 2048 bits, ainda não chegou a hora do limite.
Até o momento, os resultados são mais do que modestos. Os melhores resultados de fatoração usando o algoritmo Shore são os números 15 e 21 , que são muito menos que 2048 bits. Para os resultados restantes da tabela, foi utilizado um algoritmo de cálculo diferente, mas mesmo o melhor resultado de acordo com esse algoritmo (291311) está longe de ser real.
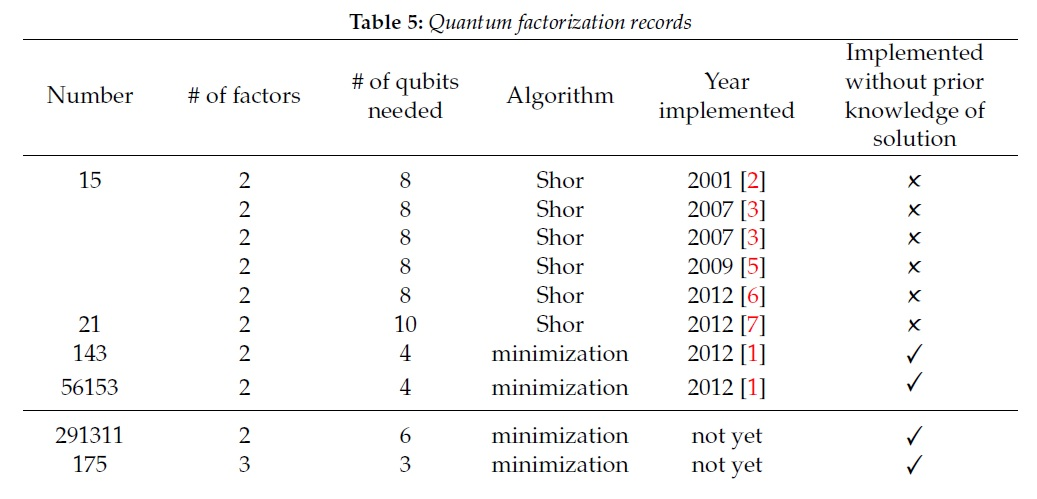
Você pode ler mais sobre o algoritmo Shore, por exemplo, aqui . Sobre implementação prática - aqui .
Uma das estimativas atuais de complexidade e energia necessárias para fatorar um número de 2048 bits é um computador com 20 milhões de qubits . Dormimos em paz.
Algoritmo de Grover
(ao conteúdo)
O algoritmo de Grover é um algoritmo quântico para resolver o problema de enumeração, ou seja, encontrar uma solução para a equação F(X) = 1 , onde F é uma função booleana de n variáveis. Foi proposto pelo matemático americano Lov Grover em 1996 .
O algoritmo de Grover pode ser usado para encontrar a média mediana e aritmética de uma série numérica. Além disso, ele pode ser usado para resolver problemas de NP-completo , pesquisando exaustivamente entre as muitas soluções possíveis. Isso pode levar a um aumento significativo na velocidade em comparação com algoritmos clássicos, embora sem fornecer uma " solução polinomial " em geral . (C)
Você pode ler mais aqui ou aqui . Também há uma boa explicação do algoritmo no exemplo das caixas e da bola, mas, infelizmente, por razões fora do meu controle, este site não me é aberto da Rússia. Se o seu site também estiver bloqueado, aqui está um breve aperto:
Algoritmo de Grover. Imagine que você tenha N pedaços de caixas fechadas numeradas. Todos estão vazios, exceto aquele em que a bola está localizada. Sua tarefa: descobrir o número da caixa em que a bola está localizada (esse número desconhecido é frequentemente indicado pela letra w).

Como resolver este problema? , , . , ? N/2. , 100 , 100 , , .
. , , (Oracle). — « 732», « 732 ». , , « , »
, , , : N SQRT(N) !
.
-
( )
— ( — ) — [ ]( https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D1%8B%D0%B9 %D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC), 1992 , , . _
— , F(x1, x2, … xn) ( 0, 1 ) ( 0, 1). , , . ()
. :
( — ) , . , . : «» «» – , «», «» — . , , – . ()
( )

, . ( ) :
“ ”, .
:
( )
N+1 .
, , ( ) . , , — .
, (-273.14 ) - , () .
, , .
.
, . — IBM IBM Q System One Google Sycamore . , (2) 200 .
Sycamore, — 1 200 , — 130 . 150 . ? .
?
, 150 N — .
:
150 . — .
...
( )

, , 100% , - . , . :
, , , . , , . , , , .
— () , , , . — “ ?” — 5050, .
, ( ) - . . N 1 .
— . , 100 , 80 , 20.
— , . .
. , — IBM IBM Q System One Google Sycamore :
— . 1-Fidelity. , 2- .
2016 NQIT .
( )

, . () , , .
1- , , 12-, , , . , , , , .
, , , “ ” “” . .
:
, , . , , . - , .
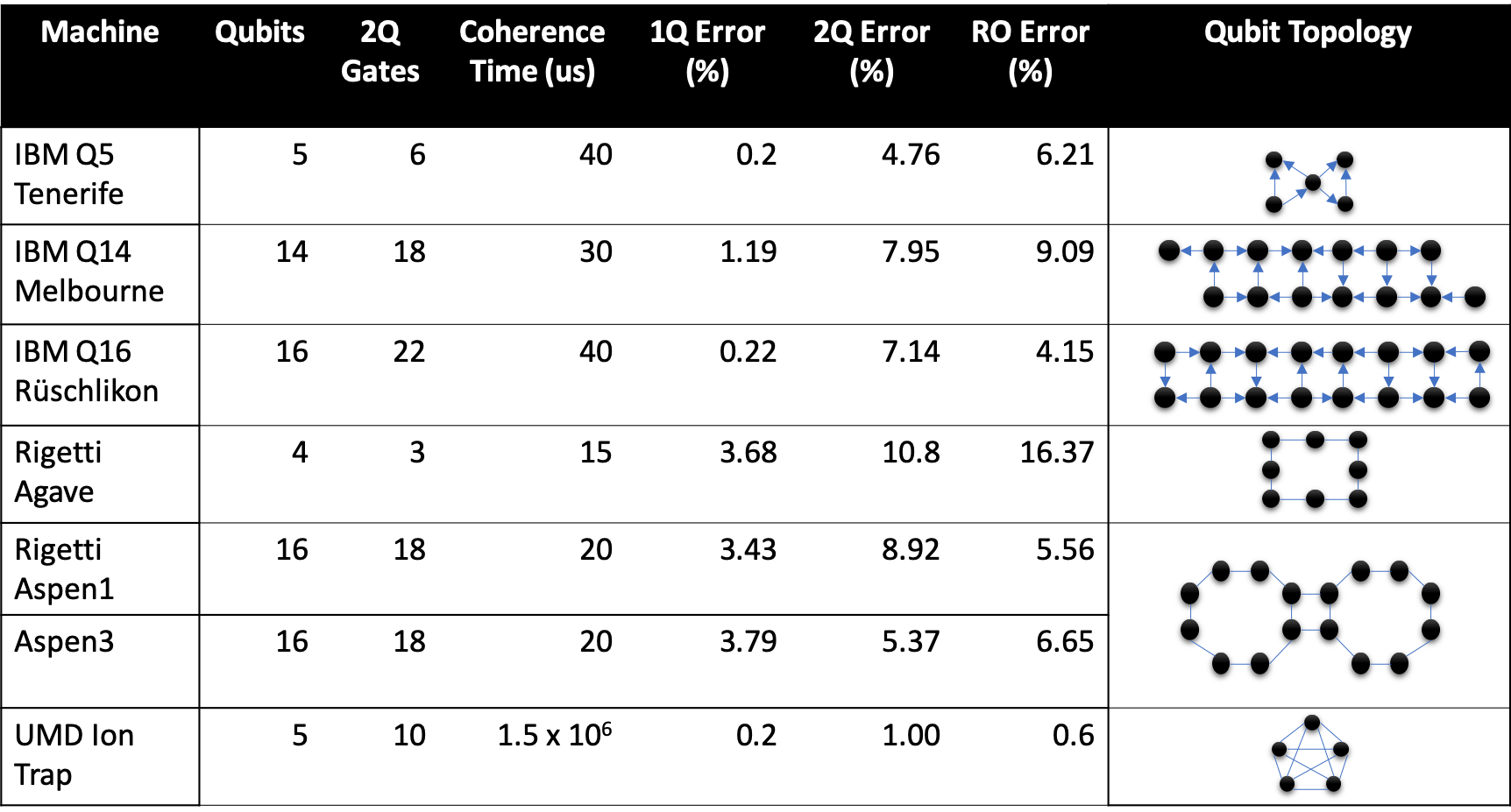
:
( )
— . 150 :
, 0.5 , :
We measure a qubit coherence time in excess of 0.5 s, and with magnetic shielding we expect this to improve to be longer than 1000 s
, , .
, , , .
, , , 1 4 1 6.
( )
, :
, , ( ) , . ( ), , .
D-Wave
( )

2000- D-Wave 2000Q. : D-Wave Systems
Google 53- , D-Wave, , . , 53 , 2048 ? ...
( ):
D-Wave ( ), , .
, , , (, ), Scott Aaronson . , ,
D-Wave. , 2014 IBM , D-Wave . , 2015 Google NASA , , , . Google , , .
, D-Wave, . , . , — . , D-Wave ASIC .
( )
. , :
- , 232 264 (8-16 )
- N 2^N , .. 2^(3+N) 32- 2^(4+N) 64- .
- N 2^N x 2^N
:
()
, Summit ( Top-1 Top-500 ) 2.8 .
— 49 ( Sunway Taihu Light )
.
. :
— 49 - 39 "" ( ) 2^63 — 4 4
50+ . - Google 53- .
.
( )

:
́ ́ — , .
, , , , , . .
, “ ”. , 50+ , , , . .
, . , Google, Sycamore .
Google
( )

54- Sycamore
, 2019 Google Nature « ». 54- «Sycamore».
Sycamore 54- , 53-. , , 54- , . , 53- .
, .
IBM , Google . , 2,5 , , . .
, , Scott Aaronson . Scott's Supreme Quantum Supremacy FAQ! , . FAQ, , , .
Google? , :
, , , . : (.. 1- 2- — — , 20, 2D n=50-60 ). , 0, {0,1}, n- () . , , .
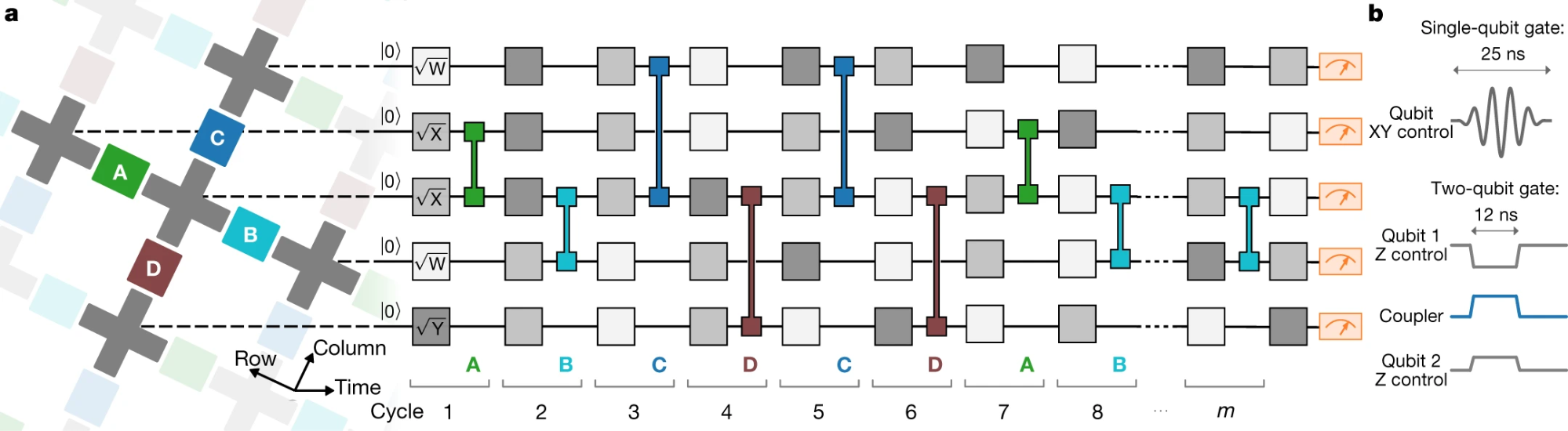
:
Google 53- , .
— Google , , , , , . , 2048- .
Sumário
( )

— , .
(-) :
:
:
:
( ), , - , .
— , , . .
Conclusão
( )
, , , , D-Wave Google .
(, , ..) , , , , .. , .
, - .
() Kruegger
( )

@Oxoron , “ ”
@a5b - “ ” , , .
, .
( )

[The National Academies Press]