O paradoxo de Einstein - Podolsky - Rosen nos dedos e ... o que o éter tem a ver com isso

O paradoxo de Einstein - Podolsky - Rosen é agora estudado ativamente em muitos laboratórios do mundo e institutos científicos. Toneladas de artigos científicos estão sendo escritos. Muita publicidade foi suscitada em círculos quase científicos.


Apenas um obstáculo, embora bastante paradoxal. Na própria mecânica quântica, não há nada paradoxal no paradoxo da EPR! Nem um grama!

Então, por que está sendo estudado tão de perto?

E sim, o que o éter tem a ver com isso ?!

Procure por nova física

A resposta é simples - ao estudar o paradoxo da EPR, há uma busca ativa por nova física. Para ser preciso - a busca por uma nova física fundamental, à medida que o desenvolvimento da física aplicada prossegue.

Isto é especialmente verdade em nosso mundo, onde bolas são governadas por teorias da conspiração que sugerem que reptilianos ou judeus em algum lugar estão escondendo a física REAL!

Antagonista do final do século XIX, quando muitos físicos acreditavam que quase tudo estava aberto, restava apenas encontrar alguns retoques.

Agora, pelo contrário, até físicos conservadores pensam que a física fundamental está longe de ser completa.

Naturalmente, o interesse em encontrar nova física é agora colossal!

Uma coisa ainda precisa ser entendida: como determinar onde procurar esse veio de ouro da nova física?
Uma opção é encontrar inconsistências nas teorias e tentar cavar lá.

Tomemos, por exemplo, a teoria eletrodinâmica de Maxwell. Essa teoria é tão bem consistente com todas as teorias aceitas que não há nada a procurar. E não olhe. Bem, exceto por teorias unificadoras. À tarde com fogo, você não encontrará novos artigos sobre eletrodinâmica fundamental. Embora aplicado - um monte.

Coordenação de STO e GO

No entanto, a eletrodinâmica é difícil de mostrar bem nos dedos, então vamos usar algo mais simples.
Vamos ver até que ponto a Teoria Especial da Relatividade concorda com a Mecânica Clássica (principalmente com a relatividade de Galileu).

A relatividade de Galileu, em particular, fala da relatividade da velocidade.

E a Teoria Especial da Relatividade, em particular, afirma que a velocidade da luz é absoluta.
Parece que o conflito é óbvio. Mas nós (na pessoa de Einstein) declaramos o STR como uma teoria generalizada do GO, onde a relatividade de Galileu é apenas um caso especial.

De fato, se nas transformações de Lorentz direcionamos a velocidade da luz para o infinito $$ , então obtemos a transformação do Galileo. Ou, em outras palavras, para velocidades muito inferiores à velocidade da luz, as transformações do Galileo serão válidas.

Portanto, não vale a pena procurar uma nova física na junção da mecânica clássica e especial. E há muito poucos artigos novos sobre esse assunto. Isso não significa que tudo foi desenterrado na estação de serviço. Você pode procurar um novo, por exemplo, no campo dos taquiões (partículas com velocidades mais altas que a luz) e sim, eles estão procurando lá.

Coerência da mecânica quântica e clássica

Mas e a consistência da mecânica quântica e clássica?
A mecânica clássica afirma em particular que partículas existem aqui e agora.
E a mecânica quântica afirma que as partículas são ondas, manchadas no tempo, no espaço e até em nós mesmos.

Aqui também o conflito é óbvio. Mas você também pode sair: declaramos o KM uma teoria generalizada da mecânica clássica (newtoniana).

De fato, se nas soluções das equações de Schrödinger, filmarmos a constante de Planck (reduzida) até zero $$ então temos leis newtonianas. Bem ... QUASE.

Ou, em outras palavras, se trabalharmos a distâncias muito maiores que o comprimento de onda de De Broglie, podemos usar as equações newtonianas. Bem ... QUASE.
De fato, isso não é suficiente. E o que é mais incompreensível - não sabemos o que mais precisa ser mudado na mecânica quântica, exceto o colapso da função de onda, para obter a Mecânica Newtoniana.



Uma das inconsistências mais impressionantes e simples entre essas duas teorias é o paradoxo dos gatos de Schrodinger.

O paradoxo de Schrödinger afirma que, se pegarmos um único átomo radioativo e colocarmos um detector de radiação próximo a ele como detonador (veneno ou bombas). Aquele gato ao lado deste dispositivo:

• De acordo com a mecânica clássica - estará OU vivo OU morto de qualquer maneira
• De acordo com a mecânica quântica - se o gato com o dispositivo estiver em uma caixa impenetrável - então - E vivo E morto ao mesmo tempo, e apenas a publicação de informações o forçará a mudar para o modo OR / OR

Pode parecer que a mina de ouro da nova física foi encontrada, vá e cave, mas não tão simples.
O fato é que a parte que contradiz está localizada no campo do paradoxo mundial do canguru (de fato, o complicado paradoxo do bule de chá de Russell).

Ele afirma que quando fechamos os olhos e desligamos os aparelhos, tudo ao redor se transforma em um canguru. Mas se ligarmos os aparelhos ou abrirmos os olhos, tudo se transformará no que vemos.
O paradoxo é que esses mundos não podem ser provados nem refutados em princípio e geralmente são descartados pela navalha de Occam.

Isso significa que, embora tenhamos encontrado uma discrepância entre a mecânica quântica e a newtoniana - não há lugar para investigar - não é possível fazer um único experimento que tenha provado ou refutado uma das versões.

Procure por nova física e éter

De fato, a idade de ouro do éter já desapareceu mais de um século. O éter surgiu como um assistente para as explicações dos campos de luz, elétrico e magnético. Mas a estrela do éter brilhou mais intensamente na segunda metade do século XIX, quando Maxwell adicionou as equações de Ampère e combinou as equações básicas de eletricidade e magnetismo em um sistema, criando a teoria do eletromagnetismo.
Resolvendo essas equações diferenciais, em particular, verificou-se que existem ondas eletromagnéticas e que essas ondas se movem a uma velocidade constante $$ onde $$ - magnético e $$ - constante dielétrica do vácuo. Um pouco mais tarde, descobriu-se que essa velocidade é muito semelhante à velocidade da luz medida em breve, a partir da qual se concluiu que a luz são as ondas eletromagnéticas de Maxwell.

No entanto, a declaração em si tinha duas desvantagens:

• Quando falamos de ondas, queremos dizer o ambiente em que essas ondas se propagam. Ondas do mar - na água, som - no ar. E no que as ondas eletromagnéticas se propagam?
• O movimento das ondas com velocidade constante era claramente contrário à relatividade das velocidades de Galileu.

E se a primeira é uma questão mais filosófica, então no segundo caso, algo não estava certo.
Ou Galileu estava certo (e o princípio da relatividade da velocidade é óbvio demais para uma contradição), ou Maxwell estava certo (embora o que é mais intuitivamente mais correto - uma solução para o princípio difuso ou óbvio?!), Ou ambos estivessem certos (é terrivelmente difícil mudar o problema) montagem sob Galileo).



A teoria do éter luminífero removeu toda a tensão - em primeiro lugar, descobriu-se que as ondas eletromagnéticas se propagam no éter, e a velocidade da luz é constante em relação ao éter estacionário, mas o movimento do éter em si é muito relativo. Isto é, Maxwell e Galileu estão certos. Bem ... teoricamente.

É verdade que a prática não parou. Medições cada vez mais precisas não mostraram desvios da velocidade da luz, nenhum vento etéreo pôde ser detectado.

Lorentz percebeu que o éter oculta e muda o espaço e o tempo de tal maneira que parece que não há vento etéreo e a velocidade da luz é constante.

Einstein em 1905 apenas removeu a essência desnecessária e criou a Teoria Especial da Relatividade com base nas transformações de Lorentz. Então o éter perdeu metade das funções.

Finalmente, o éter luminífero morreu desnecessariamente um pouco mais tarde, com o desenvolvimento da mecânica quântica, e foi a descoberta da dualidade onda-partícula em 1924. A luz não precisa mais de um mediador, e / m as ondas se propagam no próprio fóton.

Procure por nova física em não localidade

Da mesma forma, estamos procurando uma discrepância entre a mecânica clássica e a quântica, mas para podermos confirmar isso com experimentos e tentar encontrar uma explicação.

Estes são experimentos com violação da localidade. Os cientistas têm mais que certeza de que o mundo é local (não há interação de longo alcance, as partículas se comunicam usando assistentes como um fóton e outros bósons de medição).

Por outro lado, alguns dos resultados da mecânica quântica são claramente não-locais.

Efeitos não locais da luz polarizada

Não, não veremos algo complicado, como o paradoxo da EPR. Para realizá-lo, usaremos um experimento muito mais fácil - a não-linearidade dos efeitos da polarização da luz. Para fazer isso, não precisamos de ferramentas ou instituições mega complexas. Basta ir à loja de equipamentos fotográficos e comprar 2 filtros polarizados linearmente. E é isso.

Por experiência, colocaremos os dois filtros paralelos um ao outro e iluminaremos com uma lanterna. Se os filtros forem ideais, todo o feixe de luz que passou pelo primeiro filtro passará pelo segundo sem perda. Se houver blecaute, é considerado separadamente como um coeficiente constante.



Portanto, se a polarização do segundo filtro paralelo estiver em um ângulo em relação ao primeiro filtro (ou vice-versa), o coeficiente de transmissão final de acordo com a mecânica quântica é

$$

Ou seja, se o ângulo for zero, 100% da luz passa, se 90 ° - a luz está completamente bloqueada - 0% passa. Se o ângulo for 45 °, metade do feixe passa 50%. Etc.



A prática mostra (a lei de Malus descobriu no início do século 19) que ela concorda muito bem com a teoria.

E agora a coisa mais importante:

Se as decisões são tomadas individualmente por cada partícula individualmente sem se comunicar com ninguém, essas decisões não podem ser explicadas usando a localidade.

Se você puder - vá em frente, preencha um artigo e receba seu Nobel!

O que podemos explicar com a ajuda da localidade é uma dependência linear, de modo que a 0 ° passa 100%, a 45 ° passa 50% e a 90 ° passa 0%. No entanto, em quaisquer outros ângulos, os valores não convergem.

Agora haverá homens sábios e dirão, deixe os fótons sentirem o ângulo de polarização e, de acordo com a fórmula, lançará lotes. Taki terá que complicar as experiências para uma correspondência mais exata: exatamente individual, exatamente sem comunicação ...

Não localidade no paradoxo de Einstein-Podolsky-Rosen

O próprio paradoxo da EPR afirma que é possível medir simultaneamente as propriedades quânticas violando o princípio da incerteza de Heisenberg, o que significa que a mecânica quântica é incompleta.

Bohm sugeriu experimentos para verificar esse paradoxo com a ajuda de fótons ou elétrons emaranhados.



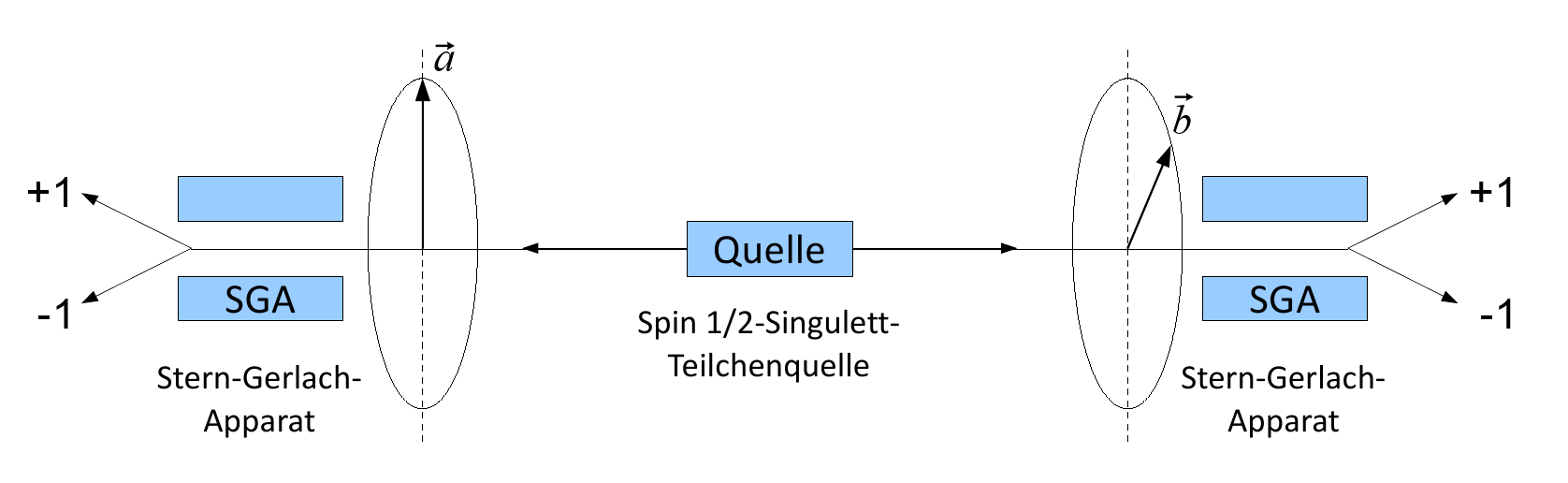
Imagine um experimento em que 2 elétrons se espalhem linearmente a partir do centro e ambos passam por 2 medidores de rotação paralelos.

Para começar, entenderemos o que acontecerá se os elétrons forem comuns, não emaranhados.

Tudo é simples. Elétrons de rotação passarão pelo primeiro medidor $$ em 50% dos casos e 50% dos casos $$ . Através do segundo - tanto.

E se girarmos os medidores, qual será o resultado?
Teremos uma média de 50% $$ e 50% dos casos com $$ . Trivial.

Agora vamos complicar e tentar encontrar as dependências.

Vamos saber que uma partícula com um giro passou pelo primeiro metro $$ . Caso contrário, ignore o resultado da passagem da segunda partícula. A questão é o que passará pelo segundo medidor, caso o primeiro seja $$ ? Obviamente - com uma probabilidade de 50% mostrará o giro $$ e com uma probabilidade de 50% $$ .

Por conveniência, introduzimos o índice de correlação, que é igual ao módulo da diferença de probabilidade de ambas as opções:

$$

Nossa correlação é zero.

O dispositivo possui outro grau de liberdade: os medidores de rotação podem ser girados independentemente um do outro. E o que acontecerá se uma partícula com um giro passar pelo primeiro metro $$ e o segundo medidor é girado 90 ° em relação ao primeiro. Obviamente - uma média de 50% $$ e 50% dos casos com $$ . E, novamente, a correlação é zero.

Em geral, onde quer que você vire, não haverá correlação.



Mas isso se torna muito mais interessante quando enviamos elétrons emaranhados.

As partículas emaranhadas são muito simples: elas SEMPRE têm um giro para trás em relação uma à outra.

Se o primeiro girar $$ , então o segundo elétron emaranhado necessariamente tem $$ girar.

E se o primeiro tem um giro $$ então o segundo - $$ .
Ou seja, uma correlação de 100%.

Mas o que acontece se girarmos o segundo cursor em 90 °? Se o primeiro girar $$ , o segundo elétron emaranhado terá uma média de 50% $$ e 50% dos casos com $$ . Acontece que a correlação é zero.

O que acontece se girarmos o segundo cursor em 45 °? Se o primeiro girar $$ então o segundo elétron emaranhado terá 25% de chance $$ e 75% de chance $$ . Correlação de 50%.

No caso geral, obtemos da teoria e da prática o nível de correlação dependendo do ângulo mútuo dos medidores de rotação:

$$

Isto é, de fato, obtivemos a mesma equação não linear que para a passagem de fótons através de filtros.

Você pode tentar descrever a não linearidade local usando parâmetros ocultos, mas a desigualdade de Bell para parâmetros aleatórios ocultos será violada.

A teoria de Bell na formulação de Clauser-Horn-Shimoni-Holt diz que, para quatro variáveis ​​aleatórias, a desigualdade sempre será verdadeira:

$$

onde K é a correlação sem módulo (e pode ser negativo).



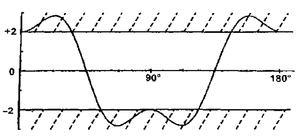
Somente para esses experimentos, a desigualdade será violada em alguns ângulos (próximos a 0 ° e 90 °), o que significa que eles não podem ser explicados por parâmetros ocultos aleatórios.

Conclusões

Enquanto na junção da mecânica clássica e quântica, o clássico perde a seco. E até nos faz pensar que não sabemos algo sobre a localidade da natureza, se é mesmo local ...