O estudo dos neutrinos levou a uma descoberta inesperada na matemática

Três físicos queriam calcular o processo de mudança de neutrinos. Como resultado, eles encontraram uma relação inesperada entre alguns dos objetos mais comuns da matemática.

Um dia em agosto, na manhã seguinte ao café da manhã, o matemático Terence Tao abriu um e-mail escrito por três físicos com quem ele não estava familiarizado. Trinity explicou-lhe que tinha encontrado uma fórmula simples, que, se verdadeira, descreveria uma relação inesperada entre alguns dos objetos mais básicos e importantes da álgebra linear.

A fórmula "parecia boa demais para ser verdade", disse Tao, professor da Universidade da Califórnia, Los Angeles, vencedor do Fields , um dos principais matemáticos do mundo. "Algo tão curto e simples deveria estar nos livros didáticos há muito tempo", disse ele. "Portanto, a princípio pensei - não, não pode ser."

E então ele pensou um pouco mais.

Físicos - Stephen Park do National Accelerator Laboratory. Fermi, Xining Zhang, da Universidade de Chicago, e Peter Denton, do Laboratório Nacional Brookhaven - obtiveram essa identidade matemática dois meses antes, tentando lidar com o estranho comportamento de partículas elementares chamadas neutrinos .

Eles notaram que “ vetores próprios ”, difíceis de calcular, descrevendo, no seu caso, como os neutrinos se propagam na matéria, são comparados a uma combinação de termos conhecidos como “valores próprios”, que são muito mais fáceis de calcular. Além disso, eles perceberam que essa relação entre autovetores e autovalores - muito comum em objetos de cálculos de matemática, física e engenharia que foram estudados desde o século XVIII - parece ser de ordem mais geral.

Embora os físicos não pudessem acreditar que descobriram um fato novo relacionado a essa matemática básica, eles não conseguiram encontrar essa relação nos livros ou nos artigos. Portanto, eles decidiram arriscar e entrar em contato com Tao, apesar de ter sido feito um pedido em seu site para não incomodá-lo nesses casos.

"Para nossa surpresa, ele respondeu duas horas depois e disse que nunca tinha visto algo assim antes", disse Park. Além disso, na resposta de Tao havia três provas independentes dessa identidade.


Xining Zhang, Peter Denton e Stephen Park com a fórmula aberta

Uma semana e meia depois, os físicos e Tao, a quem Park chama de "mangueira de incêndio da matemática", publicaram um artigo na Internet relatando uma nova fórmula. Agora, este trabalho é avaliado por especialistas da revista Communications in Mathematics Physics. Em um artigo separado publicado no Journal of High Energy Physics, Denton, Park e Zhang usam essa fórmula para simplificar as equações que descrevem o comportamento dos neutrinos.

Os especialistas dizem que essa fórmula pode ter mais maneiras de aplicar, porque em um grande número de tarefas, é necessário o cálculo de vetores e valores próprios. "Ele tem uma ampla variedade de usos", disse John Bickom , especialista em física de partículas na Universidade de Ohio. "Quem sabe que portas ela pode abrir."

Os matemáticos pensam da mesma maneira. "Isso é surpreendente e interessante", disse Van Wu , matemático da Universidade de Yale. "Eu não suspeitava que era possível calcular vetores próprios usando apenas informações sobre valores próprios".

Vu e Tao provaram uma identidade semelhante em 2009 (foi por isso que Denton, Park e Zhang decidiram entrar em contato com Tao), mas a nova fórmula obviamente não segue a antiga. E embora uma fórmula semelhante por acaso tenha aparecido em um trabalho matemático em maio deste ano, seus autores não a associaram a autovetores e autovalores.

Em certo sentido, não é de surpreender que uma nova idéia sobre objetos matemáticos com vários séculos de idade venha dos físicos. A natureza inspirou a pesquisa matemática desde que as pessoas começaram a contar com 10 dedos. "Para que a matemática floresça, ela precisa estar conectada à natureza", disse Vu. "Não há outro caminho."

Truques de transformação

Os vetores próprios e os valores próprios são tão comuns porque caracterizam transformações lineares: operações que esticam, comprimem, giram ou de qualquer outra forma alteram igualmente todas as partes do mesmo objeto. Essas transformações são representadas por matrizes retangulares de números chamados matrizes. Uma matriz gira o objeto 90 graus; o outro vira de cabeça para baixo e reduz pela metade.


A aplicação dessa matriz a um determinado objeto espelhará a mesma em relação ao plano e também dobrará sua altura. Os autovetores da matriz descrevem as direções nas quais o objeto não muda, exceto a escala. Os autovalores da matriz descrevem o quanto o objeto escala ao longo desses autovetores.
O vetor próprio A é paralelo ao eixo vertical. Seu valor próprio é 2, porque o objeto dobra sua altura.
O vetor próprio B está no plano de reflexão. Seu valor próprio é 1, porque o objeto não muda ao longo dele.
O vetor próprio C é perpendicular ao plano de reflexão. Seu valor próprio é -1, o que significa reflexão em relação ao plano.
Ao excluir linhas e colunas de uma matriz, matrizes menores podem ser criadas. Seus valores próprios, juntamente com os valores próprios das matrizes originais, podem ser usados ​​para calcular os vetores próprios das matrizes originais.

As matrizes fazem isso alterando os “vetores” dos objetos - setas matemáticas apontando para cada local físico do objeto. Os autovetores de uma matriz são aqueles vetores que continuam apontando na mesma direção de antes, após a aplicação da matriz. Suponha que tomemos uma matriz que gire um objeto 90 graus em torno do eixo x: os autovetores são direcionados ao longo do eixo x, pois os pontos localizados nesse eixo não giram quando todos os outros giram em torno deles.

Uma matriz semelhante pode girar objetos ao redor do eixo x e compactá-los duas vezes. Quanto a matriz comprime ou estica os autovetores do objeto, descrevem os autovalores correspondentes - neste caso, 1/2 (se o autovetor não mudar, seu autovalor será 1).


Terence Tao

Os vetores próprios e os valores próprios são independentes e, geralmente, precisam ser calculados separadamente, começando pelas linhas e colunas da própria matriz. Os alunos aprendem a fazer isso em matrizes simples. Mas a nova fórmula é diferente dos métodos existentes. "O que é interessante sobre essa identidade é que você não precisa conhecer nenhum valor contido na matriz para calcular algo", disse Tao.

A identidade é aplicada a matrizes hermitianas que realizam transformações reais de vetores próprios (em contraste com números imaginários) e, portanto, são aplicáveis ​​a situações que ocorrem na realidade. A fórmula expressa cada vetor próprio da matriz hermitiana em termos dos valores próprios dessa matriz e de sua “matriz menor” - uma matriz menor, que é obtida pela exclusão da linha e coluna do original.

Olhando para trás, a fórmula parece razoável, disse Tao, já que os valores próprios da matriz menor codificam informações ocultas em si mesmos. No entanto, "por exemplo, eu pessoalmente nunca teria pensado nisso."

Ele disse que uma ferramenta não relacionada a uma tarefa raramente aparece em matemática. No entanto, ele acredita que a interconexão de autovetores e autovalores deve ser importante. "É tão bonito que tenho certeza de que a fórmula encontrará alguma aplicação em um futuro próximo", disse ele. "Até agora, temos apenas um uso para ela."

Partículas de lobisomem

E essa aplicação está associada aos neutrinos: a mais estranha, menos estudada e mais secreta das partículas fundamentais conhecidas. A cada segundo, trilhões de partículas passam pelo corpo humano, mas, como praticamente não mostram sua presença, muitas de suas propriedades permanecem desconhecidas.

Curiosamente, a teoria afirma que são precisamente as diferenças no comportamento dos neutrinos e antineutrinos que podem fazer com que a matéria domine a antimatéria no Universo . Se os dois opostos aparecessem depois do Big Bang em quantidades iguais, eles se aniquilariam e não restaria nada no espaço, exceto a luz. A diferença entre um neutrino e um antineutrino pode dar origem a um excesso vital de matéria. "Se eles se comportarem de maneira diferente, nos dará uma idéia de por que o Universo está cheio de matéria", disse Deborah Harris , física da Universidade de York e Fermilab, trabalhando no experimento DUNE (Deep Underground Neutrino Experiment, um neutrino subterrâneo profundo) experimento) projetado para medir essas diferenças.

O experimento, que medirá as características dos neutrinos lançados do Fermilab, em Illinois, para um detector subterrâneo localizado a 1300 km da fonte em Dakota do Sul, usa o fato de que existem três tipos diferentes de neutrinos - elétron, múon e tau. No entanto, cada tipo é uma mistura mecânica quântica e os neutrinos oscilam, mudando seus tipos em movimento. À medida que os neutrinos viajam do Fermilab, sua mistura muda, então o múon neutrino pode se transformar em elétron ou tau neutrino.

Essas oscilações são descritas por uma matriz 3x3 extremamente complexa. Com base nos vetores próprios e nos valores próprios, os físicos podem calcular uma expressão descrevendo a probabilidade de um neutrino de múon se transformar em neutrino eletrônico quando chegar a Dakota do Sul. Eles também calculam a probabilidade de um neutrino de múon se tornar um antineutrino de elétrons.


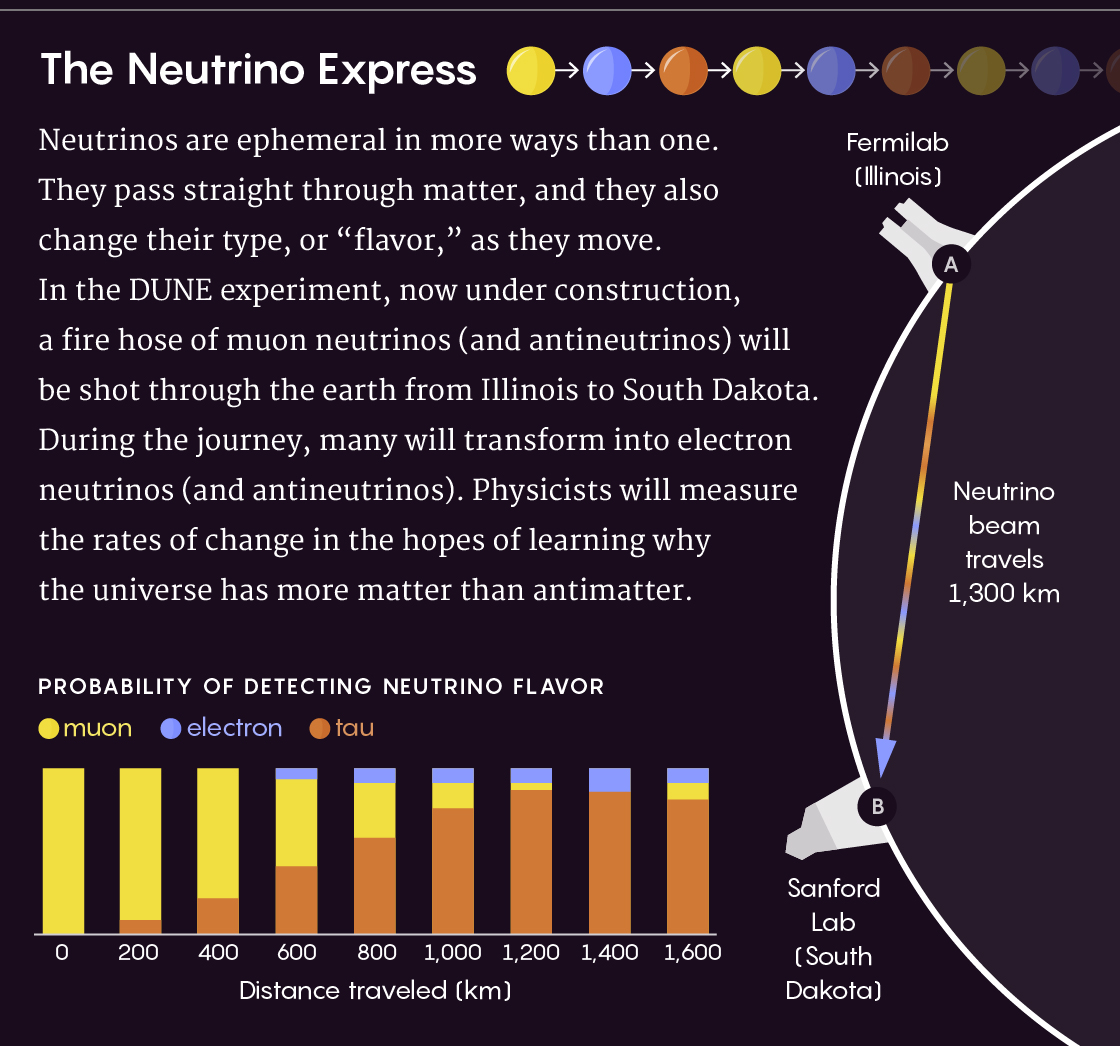As partículas efêmeras de um neutrino não apenas passam pela matéria, mas também mudam de tipo na hora. No experimento DUNE, um feixe de neutrinos será lançado, muitos dos quais mudarão de tipo no caminho da fonte para o alvo. Essas mudanças serão medidas pelos físicos.
O diagrama mostra a probabilidade de detectar neutrinos de vários tipos, dependendo da distância em km. Amarelo - múon, azul - eletrônico, marrom - tau.

Essas expressões contêm o desconhecido: a “fase de violação da invariância da PC ”, que mostra como as leis das oscilações de neutrinos e antineutrinos diferem umas das outras. Medindo e comparando as taxas reais de oscilação, os cientistas com DUNE podem calcular esse desconhecido. Se a fase de perturbação for grande o suficiente, isso ajudará a explicar por que o universo está cheio de matéria.

E como se essas dificuldades não bastassem, um efeito estranho, cujos pré-requisitos foram descobertos pela primeira vez em 1978 pelo físico Lincoln Wolfenstein, torna a matriz de neutrinos ainda mais complexa. Os neutrinos raramente interagem com a matéria no sentido usual, mas Wolfenstein descobriu que sua passagem pela matéria, diferentemente do espaço vazio, ainda muda a maneira como se propagam. Às vezes, um neutrino que penetra na matéria interage com os elétrons em um átomo, essencialmente trocando de lugar com ele: um neutrino de elétron se transforma em elétron e vice-versa.

Tais substituições introduzem um novo termo na matriz, afetando os neutrinos eletrônicos, o que complica muito a matemática. É esse efeito de Mikheev-Smirnov-Wolfenstein [que foi previsto e teoricamente investigado pelos físicos soviéticos Stanislav Mikheev e Alexey Smirnov em 1985, com base no caso de oscilações de neutrinos em um meio com densidade constante considerada em Wolfenstein], pressionando Park, Zhang e Denton para encontrar uma maneira de simplificar o cálculo. .

A expressão para calcular os valores próprios é mais simples que a expressão para os vetores próprios, portanto, Park, Zhang e Denton usaram isso como ponto de partida. Antes disso, eles desenvolveram um novo método para o cálculo aproximado dos valores próprios. Com base nisso, eles notaram que expressões longas para vetores próprios de trabalhos anteriores eram iguais a combinações desses valores próprios. Juntando tudo, "você pode calcular de maneira fácil e rápida as oscilações de neutrinos na matéria", disse Zhang.

A respeito de como eles viram o padrão a partir do qual a fórmula segue, os físicos não têm muita certeza. Park diz que eles simplesmente notaram manifestações individuais do padrão e o generalizaram. Ele também admite que é bom em resolver quebra-cabeças. Ele é o co-autor de outra regularidade importante , descoberta em 1986, que facilitou os cálculos no campo da física de partículas e até hoje inspira os cientistas a novas descobertas.

E, no entanto, o fato de o comportamento estranho do neutrino poder levar ao surgimento de novas idéias relacionadas à matriz chocou muitos. "As pessoas resolvem álgebra linear há muito, muito tempo", disse Park. "Ainda estou esperando alguém me enviar um e-mail onde diz: Se você olhar para este trabalho pouco conhecido de Cauchy , então há esta fórmula na nota do terceiro apêndice."

Diferença menor

De fato, uma fórmula semelhante já era conhecida, mas ninguém percebeu, porque estava mascarada.

Em setembro, Tao recebeu outro e-mail inesperado, desta vez de Jiyuan Zhang, um estudante de graduação em matemática da Universidade de Melbourne, na Austrália. Zhang apontou para a existência de uma fórmula equivalente em uma obra que ele escreveu com seu curador Peter Forester em maio, antes do surgimento do trabalho de Tao e de três físicos. Zhang e Forrester trabalharam no campo da matemática pura, a teoria das matrizes aleatórias. Eles aplicaram essa fórmula, explorando o problema associado à solução de Tao e seus colegas em 1999.

Forester nos explicou que, pela primeira vez, essa fórmula apareceu de outra forma no trabalho de 2001, de autoria de Julia Baryshnikova , uma matemática que trabalha atualmente na Universidade de Illinois em Urbana-Champaign, em cujo trabalho foram baseados em Forester e Zhang. Mas esses matemáticos descreveram os objetos de sua identidade não como autovetores, mas como termos necessários para calcular os autovalores de certas matrizes menores que aparecem no curso da resolução de seu problema.

Forester chamou a fórmula em seu trabalho com Zhang de “idêntica” à usada por Tao e pelos três físicos. Tao chamou as fórmulas de "quase idênticas", referindo-se uma à outra da mesma maneira que os dois lados da ilusão de coelho / pato. "Algumas pessoas procuravam coelhos, outras apenas patos", disse ele.



Denton escreveu em um e-mail que a fórmula que existia antes é "próxima do resultado, mas não perfeita". Ele acrescentou que "à luz da importância dos vetores próprios para muitos problemas, ainda pensamos que nosso resultado é bem diferente do resto para considerá-lo novo".

Talvez não seja tão estranho que nesta área em um único verão depois de vários séculos, uma excitação tão repentina possa surgir. "Existem muitos exemplos de descobertas simultâneas em matemática", disse Tao. - Os resultados de alguma forma estão no ar. E as pessoas simplesmente começam a procurá-los nos lugares certos. ”