Certa vez, escrevi
um artigo no qual descrevi um modelo matemático simples da evolução de uma rede neural e sua seleção pela capacidade de adicionar números em sistemas numéricos com bases 2 e uma proporção áurea, e descobriu-se que a proporção áurea funciona melhor. Então, minha primeira experiência acabou sendo muito ruim, pois não levei em consideração várias nuances importantes relacionadas ao fato de que o erro não deveria ser levado em consideração para um neurônio, mas para um pouco de informação, então decidi melhorar meu experimento e apresentar mais algumas. ajustes.
- Decidi verificar 100 pares de amostras de 15 (amostra de treinamento) e 1000 (amostra de teste) vetores em sistemas numéricos com bases uniformemente distribuídas de 1,2 a 2 em vez de duas bases conhecidas anteriormente.
- Também fiz uma regressão linear não apenas da distância entre a base e a proporção áurea, mas também da própria base, o número de coordenadas no vetor e o valor médio da coordenada no vetor de resposta, para levar em consideração a dependência não linear do erro na base.
- Também verifiquei algumas amostras quanto à normalidade pelo critério Kolmogorov-Smirnov, ANOV, mas esses critérios mostraram que as amostras provavelmente se desviaram do gaussiano, então decidi fazer uma regressão linear ponderada em vez da usual. No entanto, a ANOVA, apesar de mostrar F um pouco menos do que antes (na região de 700-800 em vez de 800-900), mas ainda assim o resultado permaneceu mais do que estatisticamente significativo, o que significa que mais testes devem ser realizados. Como esses testes, fiz um histograma da densidade de distribuição dos resíduos de regressão e do QQ normal - um gráfico da função de distribuição desses resíduos.
Estes dois gráficos são:
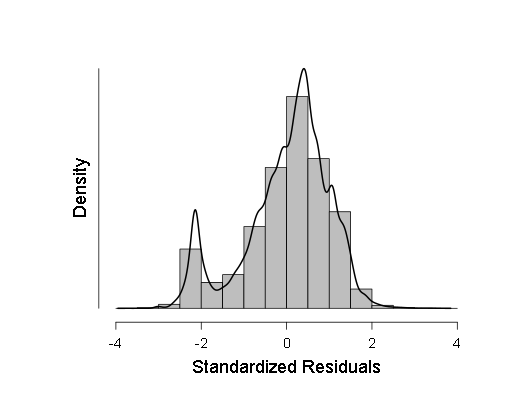
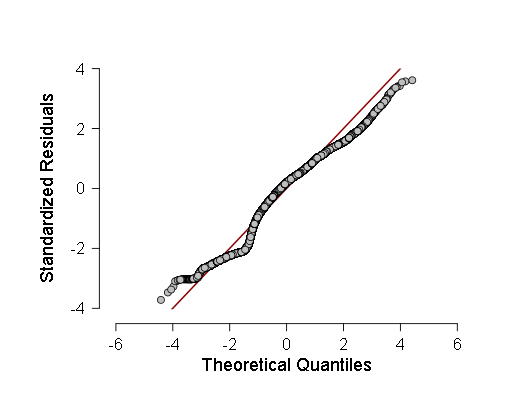
Como pode ser visto, embora o desvio da distribuição normal na distribuição dos resíduos seja estatisticamente significativo (e à esquerda, até um pequeno segundo modo é visível no histograma), na verdade, é muito próximo do gaussiano, portanto, é possível (com cautela e intervalos de confiança maiores) contar com essa regressão linear .
Agora, sobre como eu gere amostras para testar redes neurais sobre elas.
Aqui está o código para gerar as amostras: E aqui está o código do arquivo de cabeçalho: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); void calculus(double a, double x, bool *t, int n);// x a t n . void calculus(double a, double x, bool *t, int n) { int i,m,l; double b,y; b=0; m=0; l=0; b=1; int k; k=0; i=0; y=0; y=x; // t . for (i=0;i<n;i++) { (*(t+i))=false; } k=((int) (log((double)2))/(log(a)))+1;// , . while ((l<=k-1)&&(m<nk-1)) // x a ( ), { m=0; if (y>1) { b=1; l=0; while ((b*a<y)&&(l<=k-1)) { b=b*a; l++; } if (b<y) { y=yb; (*(t+kl))=true; } } else { b=1; m=0; while ((b>y)&&(m<nk-1)) { b=b/a; m++; } if ((b<y)||(m<nk-1)) { y=yb; (*(t+k+m))=true; } } } return; }
Também decidi postar o código completo da rede neural: Em seguida, vamos falar sobre como eu conduzi uma regressão linear ponderada. Para fazer isso, simplesmente calculei os desvios padrão dos resultados da rede neural e, em seguida, dividi a unidade neles.
Aqui está o código fonte do programa com o qual eu fiz isso: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void) { int i; FILE *input,*output; while (fopen("input.txt","r")==NULL) i=0; input = fopen("input.txt","r");// . double mu,sigma,*x; mu=0; sigma=0; while (malloc(1000*sizeof(double))==NULL) i=0; x = (double *) malloc(sizeof(double)*1000); fscanf(input,"%lf",&mu); mu=0; for (i=0;i<1000;i++) { fscanf(input,"%lf",x+i); } for (i=0;i<1000;i++) { mu = mu+(*(x+i)); } mu = mu/1000; while (fopen("WLS.txt","w") == NULL) i=0; output = fopen("WLS.txt","w"); for (i=0;i<1000;i++) { sigma = sigma + (mu - (*(x+i)))*(mu - (*(x+i))); } sigma = sigma/1000; sigma = sqrt(sigma); sigma = 1/sigma; fprintf(output,"%10.9lf\n",sigma); fclose(input); fclose(output); free(x); return 0; };
Em seguida, adicionei os pesos resultantes à tabela, onde reduzi todos os dados obtidos como resultado do programa, bem como os valores das variáveis para calcular a regressão e, em seguida, calculei-o no JASP. Aqui estão os resultados:
Resultados
Regressão linear
Em seguida, tenho um histograma da densidade de distribuição dos resíduos de regressão padronizados:

Bem como o gráfico quantil-quantil normal de resíduos de regressão padronizados:

Em seguida, apliquei as variáveis dos coeficientes de regressão obtidos em seu curso às variáveis e realizei minha análise estatística para encontrar o mínimo mais provável da função de erro a partir da base do sistema numérico (quanto está relacionado a essas variáveis) usando o lema de Fermat, o teorema de Bayes e o teorema de Lagrange da seguinte maneira:
O fato é que a distribuição das bases do sistema numérico na amostra era obviamente uniforme, portanto, se uma certa base no intervalo (1,2; 2) é o mínimo do erro quadrático médio, então, pelo lema de Fermat, ele terá uma derivada zero, então a densidade de probabilidade dos valores A função será infinita.
Agora, sobre como eu apliquei o teorema de Bayes. Calculei os intervalos de confiança da distribuição beta (esta é a distribuição de probabilidade de "sucesso" no experimento sob a condição de n "sucessos" e m "falhas" com densidade de probabilidade
) os valores da função de distribuição (esta é a probabilidade de a variável aleatória não ser maior que o argumento) dos erros calculados, com base no fato de que, se a variável aleatória não for maior que o argumento, será "sucesso" e, se for mais, "falha". Então, usando o teorema bayesiano, aplicamos a distribuição beta da função de distribuição dos erros calculados e calculamos seus intervalos de confiança de [função de distribuição] de 99% em cada erro calculado.
Passamos para o teorema de Lagrange. O teorema de Lagrange afirma que, se a função f (x) é continuamente diferenciável no intervalo [a; b], pelo menos em um ponto desse intervalo, ela tem uma derivada igual a
. Como aplico esse teorema: o fato é que a densidade de probabilidade é uma derivada da função de distribuição; portanto, pego o valor máximo entre aqueles que são precisos em alguns intervalos, desde o erro mínimo até os erros restantes. Depois, calculo os intervalos de confiança desses valores em 98% (usando a correção de Bonferroni) usando a seguinte fórmula:
onde F1 é a extremidade esquerda do intervalo de confiança para a função de distribuição e F2 é a direita, x_i, x_1 são os erros calculados como argumento para a função de distribuição. Em seguida, o programa procura por um intervalo com a maior extremidade esquerda e a maior extremidade direita (para que o valor no intervalo seja máximo) e, em seguida, procura o máximo e o mínimo nas bases que correspondem aos erros calculados nesse intervalo. Esses máximos e mínimos são os argumentos da função de erro de baixo para cima, entre os quais se encontra o mínimo da própria função, com uma probabilidade de 98%.
Aqui está o código do programa que conduzi esta análise estatística com explicações: E aqui está o código do arquivo de cabeçalho: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); double Bayesian(int n, int m, double x);// - n "" m "", " " " " , : double Bayesian(int n, int m, double x) { double c; c=(double) 1; int i; i=0; for (i=1;i<=m;i++) { c = c*((double) (n+i)/i); } for (i=0;i<n;i++) { c = c*x; } for (i=0;i<m;i++) { c = c*(1-x); } c=(double) c*(n+m+1); return c; } double Bayesian_int(int n, int m, double x);// - ( ): double Bayesian_int(int n, int m, double x) { double c; int i; c=(double) 0; i=0; for (i=0;i<=m;i++) { c = c+Bayesian(n+i+1,mi,x); } c = (double) c/(n+m+2); return c; } // : void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu); void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu) { double y,y1,y2; y=(double) n/(n+m); int i; for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.5)/Bayesian(n,m,y); } mu = y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.995)/Bayesian(n,m,y); } x2=y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.005)/Bayesian(n,m,y); } x1=y; }
Aqui está o resultado do trabalho deste programa, quando dei a ela os fundamentos do sistema numérico e os resultados da regressão:
x (- [1.501815; 1.663988] y (- [0.815782; 0.816937]
("(-" nesse caso é apenas uma notação do sinal "pertence" à teoria dos conjuntos, colchetes indicam o intervalo.)
Assim, me ocorreu que a melhor base do sistema numérico em termos do menor número de erros na transmissão de informações está no intervalo de 1,501815 a 1,663988, ou seja, a proporção áurea cai completamente nele. É verdade que fiz uma suposição ao calcular o mínimo e mais uma vez ao calcular a quantidade de informações em diferentes sistemas numéricos: primeiro, assumi que a função de erro da base é continuamente diferenciável e, segundo, que a probabilidade de que o número distribuído uniformemente seja 1, 2 a 2 terá o número um em um dígito específico, será aproximadamente o mesmo depois de algum dígito após o ponto decimal.
Se fiz algo completamente errado, ou simplesmente errado, estou aberto a críticas e sugestões. Espero que essa tentativa tenha sido mais bem-sucedida.
UPD Editei o artigo duas vezes para esclarecer alguns lugares da parte "puramente científica" e também formatou o código.
UPD2. Depois de consultar uma pessoa que entende de bioinformática (um graduado do estudo de pós-graduação da FBB MSU no IPPI RAS), decidiu-se substituir a palavra "cérebro" por "rede neural", pois eles diferem bastante.