Reconhecimento de circuitos digitais. Elemento C generalizado

Alexander Kushnerov
18/12/2019

Mesmo um engenheiro experiente às vezes pode achar difícil rotear o circuito para que os trilhos (ou fios) não interfiram no seu funcionamento adequado. Em uma primeira aproximação, o layout e o número de nós, cujos fios são conectados a cada nó e o comprimento dos fios após a ramificação, afetam a qualidade da fiação. Se considerarmos o comprimento do fio como um atraso, a operação correta dos circuitos digitais assíncronos pode não depender dos atrasos em alguns fios. No futuro, chamaremos esses fios de seguros e a ramificação de tais fios - completamente seguro (FGP). Neste artigo, mostraremos como um circuito universal de doze transistores pode tornar alguns ramos completamente seguros.

Considere o chamado esquema "borboleta" [1], [2] mostrado na Fig. 1. Este circuito gera pulsos separados peq, que podem ser usados ​​para controlar transistores de potência. Tampões na Fig. 1 indica fios seguros. O atraso de todos os outros fios é assumido como zero. A pausa entre pulsos é definida pelos atrasos dos buffers wy e wz. No futuro, não usaremos o buffer para indicar o atraso de um elemento. Fios e ramificações em todos os circuitos deste artigo foram testados quanto à segurança (persistência de saída) no Workcraft [3]. Gráficos de transição de sinal (STGs) foram obtidos a partir de circuitos, resolvendo conflitos no CSC. As ilustrações mostram STGs simplificados onde os sinais do buffer são removidos. Diagrama de tempo (TD) na Fig. 1 é construído de acordo com o STG correspondente.


Fig. 1. O circuito “borboleta”, seu STG e TD, pressupondo que os atrasos nos fios sejam zero.

Da teoria [1], [2] é sabido que o circuito do gatilho RS é sensível a atrasos nos fios no acoplamento cruzado. É por isso que os buffers nos links cruzados na Fig. 1 ausente. Assim, os dois elementos de gatilho devem estar a uma distância mínima um do outro. Se isso for difícil, dois elementos podem ser substituídos por um elemento complexo com feedback. Por exemplo, os elementos x e xb no circuito de borboleta podem ser substituídos conforme mostrado na Fig. 2. Além disso, temos o FGP na saída de um elemento complexo.


Fig. 2. Uma variante do circuito na Fig. 1 e seu STG sob a suposição de que os atrasos nos fios são zero.

A implementação dos esquemas na Fig. 1 e Fig. 2 requer 16 e 20 transistores, respectivamente. Além disso, o diagrama na Fig. 2 é mais lento, pois os inversores wb1, wb2 e o inversor dentro do elemento 2 OR-AND devem alternar duas vezes por ciclo. O desempenho lento geralmente é o preço do FGP. No entanto, existem exceções a esta regra. Por exemplo, na Fig. 3 mostra um esquema de um gatilho de contagem assíncrona (AST) [4] que possui dois FGPs.


Fig. 3. AST e seu STG sob a suposição de que os atrasos nos fios são zero.

As desvantagens do circuito na Fig. 3 são um grande número de fios e o fato de a maioria deles se cruzar. Isso pode complicar o layout, especialmente se o número de camadas com faixas for limitado ou se forem ocupadas por outros compostos. Portanto, você precisa procurar algum compromisso entre o número de fios, o número de transistores e o número de FGP. Um exemplo de tal esquema de compromisso com um FGP é o AST mostrado na Fig. 4. Esta é uma pequena modificação do circuito de [5]. Observe que aqui, como no diagrama da Fig. 2, uma base mista é usada. Para implementar esse AST sem um indicador (XOR em wi2, wi4 e g5), são necessários 26 transistores. Este é apenas dois transistores a mais que o AST na Fig. 3)


Fig. 4. Comprometa o AST e seu STG, quando os atrasos nos fios forem zero.

Observe que todos os elementos com feedback na Fig. 2 e Fig. 4 são casos especiais de um elemento C generalizado (gC). É dado como [6]: $$$y = S (x) + y \ overline {R} (x)$onde $$$S (x)$e $$$R (x)$As funções de instalação e redefinição atendem às condições $$$S (x) R (x) = 0$. Casos especiais do elemento gC também são elementos NCL, usados ​​em esquemas para processamento de dados. Observe que o maior elemento NCL possui quatro entradas e é implementado em 28 transistores [7]. Isso pode ser explicado pelo fato de que, com um número maior de transistores, os fios se tornam relativamente longos e o atraso neles começa a afetar a operação do elemento.

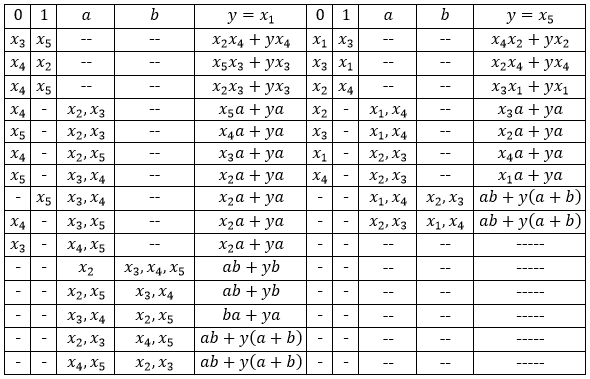
Considere o circuito do transistor mostrado na Fig. 5. Implementa a função de cinco variáveis ​​[8], [9] $$$f (x) = x_1 x_3 + x_2 x_4 + x_5 (x_1 x_4 + x_2 x_3)$. A tabela 1 mostra as funções SDNF e SKNF $$$f (x)$e sua dupla função $$$φ (x) = \ overline {f (\ overline x)}$. A partir desta tabela, é óbvio que, trocando $$$x_2$e $$$x_3$em $$$f (x)$nós temos $$$φ (x)$e vice-versa. Caso $$$x_2 = x_3 = y$, obtemos uma função auto-dupla $$$f (x, y) = \ overline {f (\ overline x, \ overline y)} = x_1 x_4 x_5 + y (x_1 + x_4 + x_5)$.


Fig. 5. Um esquema que implementa a função de cinco variáveis.

Tabela 1. Formas de funções lógicas para o circuito na Fig. 5)


Note que $$$x_2 = x_3 = y$significa que os quatro transistores correspondentes devem ser comutados ao mesmo tempo. Mesmo que os fios após a ramificação y tenham o mesmo atraso, isso não é suficiente, pois o momento de comutação do transistor é determinado pela tensão em sua porta. Deste ponto de vista, a análise do circuito na Fig. 5 foi feito em [10]. No entanto, essa análise não está completa, pois apenas a implementação de um elemento C de duas entradas foi considerada. Para fazer uma análise completa, você deve primeiro encontrar todas as opções para combinar entradas ou, mais formalmente, todas as funções de um número menor de variáveis ​​que podem ser obtidas de $$$f (x)$. Essa pesquisa foi realizada de forma um tanto simplificada e seus resultados são mostrados no apêndice. A maioria dos recursos é encontrada em várias variações. Deles é necessário escolher aqueles que dão esquemas livres de concorrência [11]. Todas as funções obtidas, o número de variantes de cada uma delas e o número da tabela correspondente no apêndice são apresentados na tabela 2. Os números com um asterisco indicam funções duplas.

Tabela 2. Os elementos gC implementados pelo circuito na Fig. 5)


As funções 2 e 2 *, 5 e 5 *, 7 e 7 * são autoduplas e a função 4 pode ser obtida da função 4 * trocando a e c. Observe que, além da função 6 *, todas as outras funções são limiares. Isso pode ser explicado pelo fato de que $$$f (x)$é isotônico (positivo unado) e o fato de que para quatro ou menos variáveis ​​as funções isotônicas coincidem com o pseudo-limiar [12]. A questão de quais opções são para as funções 1 *, 3 * e 6 * neste artigo permanece em aberto.

Considere o caso das funções 2 e 2 * como exemplo. De acordo com uma das opções (tabela P3 no apêndice) $$$x_1 = x_4 = a$e $$$x_2 = x_3 = b$. Deixe o caminho sair $$$y$desconectado da entrada $$$x_5$e deixe o sinal ser removido da entrada do inversor. Isso permite que você construa um distribuidor de transportador de célula [13] mostrado na Fig. 6. Os elementos nesta célula são diferentes, mas devido ao fato de as entradas serem combinadas, ambas implementam a mesma função auto-dupla. Observe que os elementos reticulados nos circuitos na Fig. 1, na Fig. 3 e na fig. 6 são casos especiais da construção básica para implementação perfeita [2]. Portanto, deve haver regras para transformar circuitos de projeto básico em circuitos de elementos gC e vice-versa.


Fig. 6. Distribuidor de transportador de células.

Do ponto de vista da tecnologia, os transistores devem ser "amarrados" nos barramentos de polissilício. Tal implementação do circuito na Fig. 5 é dado em [14]. Para definir os estados iniciais, os transistores p-MOS e n-MOS podem ser usados, o que cria um divisor de tensão com os transistores no inversor. A imunidade ao ruído dos circuitos pode ser aumentada com a ajuda de certas transformações STG [15].

Agradecimentos

O autor é profundamente grato a Svetlana Frolova (OmSU) pela digitalização do artigo [1], e também a Sergey Bystrov pela inspiração.

App

O MuPAD foi usado para obter os resultados apresentados nesta seção. Deixe a saída y ser conectada a apenas uma das entradas. A tabela A1 mostra que, neste caso $$$S (x) R (x) ≠ 0$. Para obter funções para as quais $$$S (x) R (x) = 0$, você pode combinar algumas variáveis ​​ou atribuir constantes a elas. As funções para o caso de combinar duas variáveis ​​são apresentadas na tabela A2. Outras opções não dão $$$S (x) R (x) = 0$. Como as quatro primeiras funções da Tabela A1 coincidem até uma permutação das variáveis, consideraremos apenas a primeira e a quinta. Estojos $$$y = y (∀)$e $$$y = (∀) + y$não é interessante, porque no primeiro só podemos redefinir o elemento gC, mas não podemos instalá-lo e no segundo - vice-versa. As manipulações com as variáveis ​​possibilitaram obter da tabela P1 as funções de quatro e três variáveis, apresentadas na tabela P3 e na tabela P4, respectivamente.

Quadro A1 Funções de cinco variáveis.


Quadro A2 Funções de quatro variáveis.


Tabela P3. Funções de quatro variáveis ​​obtidas da Tabela A1.


Quadro A4. As funções das três variáveis ​​obtidas da Tabela A1.

Literatura

[1] V. I. Varshavsky, M. A. Kishinev, A. R. Taubin e B. S. Zirlin, “Análise de circuitos lógicos assíncronos. II Acessibilidade dos estados operacionais e efeito de atrasos nos fios ”, Izv. Academia de Ciências da URSS. Cibernética técnica, não. 4, pp. 84-97, 1982.
[2] Varshavsky, V. I. (ed.), Controle automático de processos assíncronos em computadores e sistemas discretos, Nauka, 1986.
[3] workcraft.org .
[4] RC Todd, "Sistema lógico". Patente US3609569, 28 de setembro. 1971
[5] EA Vittoz, “Estrutura lógica de divisão de frequência”. Patente US3829714, 13 de agosto. 1974.
[6] J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno e A. Yakovlev, Síntese lógica para controladores e interfaces assíncronos, Springer, 2002.
[7] A. Kondratyev, “Fluxo assíncrono multi-trilho com detecção de conclusão e sistema e método para projetar o mesmo.” Patente US6526542, 25 de fevereiro 2003.
[8] JJ Gibson, "Circuitos lógicos que empregam transistores de efeito de campo". Patente US3439185, 15 de abril. 1969.
[9] R. Miller, Teoria dos circuitos de comutação. Volume I. Esquemas de combinação, Science, 1970.
[10] K. van Berkel, "Cuidado com o garfo isocrônico", Integration, vol. 13, n. 2, pp. 103-128, 1992.
[11] P. Kudva, G. Gopalakrishnan, H. Jacobson e SM Nowick, "Síntese de redes complexas de gateways CMOS personalizadas e livres de riscos sob alterações de múltiplas entradas", em Design Automation Conf., 1996.
[12] GW Fagerlin, enumeração de funções pseudo-separáveis ​​de cinco variáveis. M.Sc. tese, Universidade de Illinois, 1968.
[13] V. I. Varshavsky, A. Yu. Kondratiev, N. M. Kravchenko e B. S. Tsirlin, "Distribuidor assíncrono". Patente SU1598142, 07/10 1990.
[14] SW Cheng, "circuito lógico CMOS da árvore H", no IEEE Conf. em Eletrônica, Circuitos e Sistemas, 2008.
[15] A. Taubin, A. Kondratyev, J. Cortadella e L. Lavagno, "Transformações comportamentais para aumentar a imunidade ao ruído em especificações assíncronas", no IEEE Symp. no Async. Circuitos e Sistemas, 1999.