
O objetivo deste artigo é ensinar a rede neural a jogar o jogo da Vida sem ensinar as regras do jogo.
Olá Habr! Apresento a você a tradução do artigo "Usando uma rede neural convolucional para jogar o jogo da vida de Conway com Keras", de kylewbanks.
Se você não está familiarizado com o jogo chamado Life ( este é um autômato celular, inventado pelo matemático inglês John Conway em 1970 ), as regras são as seguintes.
O universo do jogo é uma grade infinita e bidimensional de células quadradas, cada uma das quais em um dos dois estados possíveis: vivos ou mortos (ou habitados e desabitados, respectivamente). Cada célula interage com seus oito vizinhos na horizontal, vertical ou diagonal. Em cada etapa, ocorrem as seguintes transições:
- Qualquer célula viva com menos de dois vizinhos vivos morre.
- Qualquer célula viva com dois ou três vizinhos vivos sobrevive à próxima geração.
- Qualquer célula viva com mais de três vizinhos vivos morre.
- Qualquer célula morta com exatamente três vizinhos vivos se torna uma célula viva.
A primeira geração é criada aplicando as regras acima simultaneamente a cada célula no estado inicial, o nascimento e a morte ocorrem simultaneamente em momentos distintos no tempo. Cada geração é uma função pura da anterior. As regras continuam a se aplicar à nova geração para criar a próxima geração.
Veja a Wikipedia para detalhes.
Por que fazer isso? Principalmente para entretenimento e para aprender um pouco sobre redes neurais convolucionais.
Então ...
Lógica do jogo
A primeira coisa a fazer é definir uma função que use o campo de jogo como entrada e retorne o próximo estado.
Felizmente, muitas implementações estão disponíveis na Internet, como: https://jakevdp.imtqy.com/blog/2013/08/07/conways-game-of-life/ .
De fato, ele usa a matriz do campo de jogo como entrada, onde 0 representa uma célula morta e 1 representa uma célula viva e retorna uma matriz do mesmo tamanho, mas contendo o estado de cada célula na próxima iteração do jogo.
import numpy as np def life_step(X): live_neighbors = sum(np.roll(np.roll(X, i, 0), j, 1) for i in (-1, 0, 1) for j in (-1, 0, 1) if (i != 0 or j != 0)) return (live_neighbors == 3) | (X & (live_neighbors == 2)).astype(int)
Geração de campo de jogo
Seguindo a lógica do jogo, precisamos de uma maneira de gerar campos de jogo aleatoriamente e uma maneira de visualizá-los.
A função generate_frames cria num_frames campos de jogo aleatórios com uma certa forma e uma probabilidade predeterminada de que cada célula ficará "viva", e render_frames desenha representações de imagens de dois campos de jogo lado a lado para comparação (as células vivas são brancas e as células mortas são pretas):
import matplotlib.pyplot as plt def generate_frames(num_frames, board_shape=(100,100), prob_alive=0.15): return np.array([ np.random.choice([False, True], size=board_shape, p=[1-prob_alive, prob_alive]) for _ in range(num_frames) ]).astype(int) def render_frames(frame1, frame2): plt.subplot(1, 2, 1) plt.imshow(frame1.flatten().reshape(board_shape), cmap='gray') plt.subplot(1, 2, 2) plt.imshow(frame2.flatten().reshape(board_shape), cmap='gray')
Vamos ver como são esses campos:
board_shape = (20, 20) board_size = board_shape[0] * board_shape[1] probability_alive = 0.15 frames = generate_frames(10, board_shape=board_shape, prob_alive=probability_alive) print(frames.shape)
(10, 20, 20)
print(frames[0])
[[0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1], [1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], [1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0], [0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0]])
Em seguida, uma representação inteira do campo de jogo é obtida e exibida como uma imagem.
O seguinte estado do campo de jogo também é mostrado à direita usando a função life_step :
ender_frames(frames[1], life_step(frames[1]))

Construindo conjuntos de treinamento e teste
Agora podemos gerar dados para treinamento, verificação e teste.
Cada elemento nas y_train / y_val / y_test representará o próximo campo de jogo para cada quadro do campo em X_train / X_val / X_test .
def reshape_input(X): return X.reshape(X.shape[0], X.shape[1], X.shape[2], 1) def generate_dataset(num_frames, board_shape, prob_alive): X = generate_frames(num_frames, board_shape=board_shape, prob_alive=prob_alive) X = reshape_input(X) y = np.array([ life_step(frame) for frame in X ]) return X, y train_size = 70000 val_size = 10000 test_size = 20000
print("Training Set:") X_train, y_train = generate_dataset(train_size, board_shape, probability_alive) print(X_train.shape) print(y_train.shape)
Training Set: (70000, 20, 20, 1) (70000, 20, 20, 1)
print("Validation Set:") X_val, y_val = generate_dataset(val_size, board_shape, probability_alive) print(X_val.shape) print(y_val.shape)
Validation Set: (10000, 20, 20, 1) (10000, 20, 20, 1)
print("Test Set:") X_test, y_test = generate_dataset(test_size, board_shape, probability_alive) print(X_test.shape) print(y_test.shape)
Test Set: (20000, 20, 20, 1) (20000, 20, 20, 1)
Construção de rede neural convolucional
Agora podemos dar o primeiro passo para a construção de uma rede neural convolucional usando Keras. O ponto principal aqui é o tamanho do kernel (3, 3) e a etapa 1. Eles dizem à CNN para usar uma matriz 3x3 de células circundantes para cada célula no campo que está olhando, incluindo a célula atual.
Por exemplo, se o seguinte fosse um campo de jogo e nós estivéssemos na célula do meio x , ela examinaria todas as células marcadas com um ponto de exclamação ! e célula
0 0 0 0 0 0! ! ! 0 0! x ! 0 0! ! ! 0 0 0 0 0 0
O resto da rede é bem simples, então não vou entrar em detalhes. Se você estiver interessado em algo, recomendo a leitura da documentação.
from keras.models import Sequential from keras.layers import Dense, Dropout, Activation, Conv2D, MaxPool2D
Dê uma olhada na saída da função de summary :
model.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_9 (Conv2D) (None, 20, 20, 50) 500 _________________________________________________________________ dense_17 (Dense) (None, 20, 20, 100) 5100 _________________________________________________________________ dense_18 (Dense) (None, 20, 20, 1) 101 _________________________________________________________________ activation_9 (Activation) (None, 20, 20, 1) 0 ================================================================= Total params: 5,701 Trainable params: 5,701 Non-trainable params: 0 _________________________________________________________________
Treinando e salvando um modelo
Tendo construído a CNN, vamos treinar o modelo e salvá-lo em disco:
def train(model, X_train, y_train, X_val, y_val, batch_size=50, epochs=2, filename_suffix=''): model.fit( X_train, y_train, batch_size=batch_size, epochs=epochs, validation_data=(X_val, y_val) ) with open('cgol_cnn{}.json'.format(filename_suffix), 'w') as file: file.write(model.to_json()) model.save_weights('cgol_cnn{}.h5'.format(filename_suffix)) train(model, X_train, y_train, X_val, y_val, filename_suffix='_basic')
Train on 70000 samples, validate on 10000 samples Epoch 1/2 70000/70000 [==============================] - 27s 388us/step - loss: 0.1324 - acc: 0.9651 - val_loss: 0.0833 - val_acc: 0.9815 Epoch 2/2 70000/70000 [==============================] - 27s 383us/step - loss: 0.0819 - acc: 0.9817 - val_loss: 0.0823 - val_acc: 0.9816
Este modelo fornece uma precisão de pouco mais de 98% para os conjuntos de treinamento e teste, o que é muito bom para a primeira passagem. Vamos tentar descobrir onde cometemos erros.
Experimente
Vejamos a previsão de um campo de jogo aleatório e como ele funciona. Primeiro, crie um campo de jogo e observe o próximo quadro correto:
X, y = generate_dataset(1, board_shape=board_shape, prob_alive=probability_alive) render_frames(X[0].flatten().reshape(board_shape), y)

Em seguida, vamos fazer a previsão e ver quantas células foram previstas incorretamente:
pred = model.predict_classes(X) print(np.count_nonzero(pred.flatten() - y.flatten()), "incorrect cells.")
4 incorrect cells.
Em seguida, vamos comparar a próxima etapa correta com a prevista:
render_frames(y, pred.flatten().reshape(board_shape))
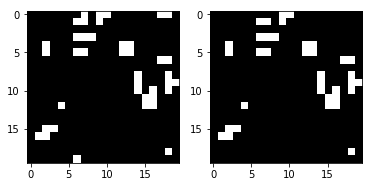
Não é assustador, mas você vê onde a previsão falhou? Parece que a rede não pode prever células nas bordas do campo de jogo. Vejamos onde valores diferentes de zero indicam previsões incorretas:
print(pred.flatten().reshape(board_shape) - y.flatten().reshape(board_shape))
[[ 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 -1 -1 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0]]
Como você pode ver, todos os valores diferentes de zero estão localizados nas bordas do campo de jogo. Vamos dar uma olhada no conjunto completo de testes e confirmar que essa observação é verdadeira.
Exibir erros usando o conjunto de testes
Escreveremos uma função que exibe um mapa de calor mostrando onde o modelo comete erros e a chamaremos usando todo o conjunto de testes:
def view_prediction_errors(model, X, y): y_pred = model.predict_classes(X) sum_y_pred = np.sum(y_pred, axis=0).flatten().reshape(board_shape) sum_y = np.sum(y, axis=0).flatten().reshape(board_shape) plt.imshow(sum_y_pred - sum_y, cmap='hot', interpolation='nearest') plt.show() view_prediction_errors(model, X_test, y_test)

Todos os erros nas bordas e nos cantos. O que é lógico, já que a CNN não pode olhar em volta, mas a lógica do jogo em life_step faz isso. Por exemplo, considere o seguinte. Olhando para a célula de borda x abaixo, a CNN vê apenas x e ! células:
0 0 0 0 0 ! ! 0 0 0 x ! 0 0 0 ! ! 0 0 0 0 0 0 0 0
Mas o que realmente queremos e o que o life_step faz é olhar para as células do lado oposto:
0 0 0 0 0 ! ! 0 0 ! x ! 0 0 ! ! ! 0 0 ! 0 0 0 0 0
Uma situação semelhante nos cantos:
x ! 0 0 ! ! ! 0 0 ! 0 0 0 0 0 0 0 0 0 0 ! 0 0 0 !
Para corrigir isso, o Conv2D deve, de alguma forma, olhar para o lado oposto do campo de jogo. Como alternativa, cada campo de entrada pode ser pré-processado para preencher as bordas do lado oposto e o Conv2D pode simplesmente excluir a primeira ou a última coluna e linha. Como estamos à mercê de Keras e da funcionalidade de preenchimento que ela fornece, que não suporta o que estamos procurando, teremos que recorrer a adicionar nosso próprio preenchimento.
Correção de defeitos nas bordas usando preenchimento
Precisamos suplementar cada campo de jogo com um valor oposto para imitar como life_step funciona para valores de borda. Podemos usar o np.pad com mode = 'wrap' para isso. Por exemplo, considere a seguinte matriz e saída aumentada abaixo:
x = np.array([ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]) print(np.pad(x, (1, 1), mode='wrap'))
[[9, 7, 8, 9, 7], [3, 1, 2, 3, 1], [6, 4, 5, 6, 4], [9, 7, 8, 9, 7], [3, 1, 2, 3, 1]]
Observe que a primeira coluna / linha e a última coluna / linha refletem o lado oposto da matriz original, e a matriz 3x3 do meio é o valor x original. Por exemplo, a célula [1] [1] foi copiada no lado oposto na célula [4] [1] e, similarmente a [0] [1], contém [3] [1]. Em todas as direções e até nos cantos, a matriz foi corrigida para conter o lado oposto. Isso permitirá que a CNN revise todo o campo de atuação e lide com casos extremos corretamente.
Agora podemos escrever uma função para preencher todas as nossas matrizes de entrada:
def pad_input(X): return reshape_input(np.array([ np.pad(x.reshape(board_shape), (1,1), mode='wrap') for x in X ])) X_train_padded = pad_input(X_train) X_val_padded = pad_input(X_val) X_test_padded = pad_input(X_test) print(X_train_padded.shape) print(X_val_padded.shape) print(X_test_padded.shape)
(70000, 22, 22, 1) (10000, 22, 22, 1) (20000, 22, 22, 1)
Todos os conjuntos de dados agora são complementados com colunas / linhas life_step , o que permite à CNN ver o lado oposto do campo de jogo, como life_step . Por esse motivo, agora cada campo de jogo tem um tamanho de 22x22, em vez dos 20x20 originais.
Em seguida, a CNN deve ser reconstruída para descartar o preenchimento usando padding = 'valid' (que instrui o Conv2D a descartar as bordas, embora isso não seja imediatamente óbvio) e manipular a nova input_shape . Assim, quando pulamos campos de jogo com um tamanho de 22x22, ainda temos um tamanho de 20x20 como saída, pois descartamos a primeira e a última coluna / linha. O restante permanece idêntico:
model_padded = Sequential() model_padded.add(Conv2D( filters, kernel_size, padding='valid', activation='relu', strides=strides, input_shape=(board_shape[0] + 2, board_shape[1] + 2, 1) )) model_padded.add(Dense(hidden_dims)) model_padded.add(Dense(1)) model_padded.add(Activation('sigmoid')) model_padded.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) model_padded.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_10 (Conv2D) (None, 20, 20, 50) 500 _________________________________________________________________ dense_19 (Dense) (None, 20, 20, 100) 5100 _________________________________________________________________ dense_20 (Dense) (None, 20, 20, 1) 101 _________________________________________________________________ activation_10 (Activation) (None, 20, 20, 1) 0 ================================================================= Total params: 5,701 Trainable params: 5,701 Non-trainable params: 0 _________________________________________________________________
Agora podemos aprender usando o campo alinhado:
train( model_padded, X_train_padded, y_train, X_val_padded, y_val, filename_suffix='_padded' )
Train on 70000 samples, validate on 10000 samples Epoch 1/2 70000/70000 [==============================] - 27s 389us/step - loss: 0.0604 - acc: 0.9807 - val_loss: 4.5475e-04 - val_acc: 1.0000 Epoch 2/2 70000/70000 [==============================] - 27s 382us/step - loss: 1.7058e-04 - acc: 1.0000 - val_loss: 5.9932e-05 - val_acc: 1.0000
A precisão da previsão é de 98% a 100%, que recebemos antes de adicionar o recuo. Vejamos o erro no caso de teste:
view_prediction_errors(model_padded, X_test_padded, y_test)

Ótimo! O mapa de calor preto indica que não há diferenças nos valores, e isso significa que previmos com sucesso cada célula para cada jogo.
Foi um pequeno exercício divertido brincar com redes neurais convolucionais sem usar um grande conjunto de dados. Sinta-se livre para conferir no GitHub .