Talvez seja difícil chamar as cúpulas geodésicas de algo incomum ou novo. Neste artigo, falarei um pouco sobre esses projetos em geral, sobre sua estrutura e também mostrarei, como exemplo, como considerei algo sobre esse tópico. O código também será.
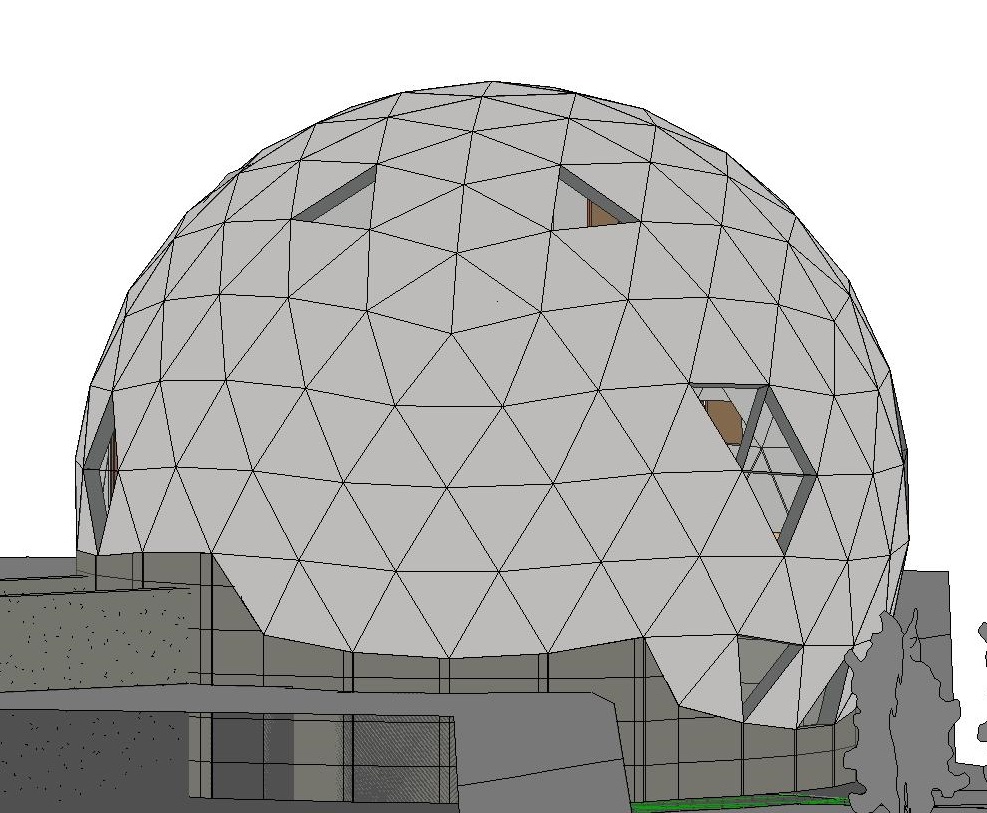
Não vou citar a Wikipedia. Por que escolhi a cúpula como minha casa?
- Com um volume igual, a área da superfície da esfera será menor que a de qualquer outra forma. Isso afeta positivamente o consumo de material e o consumo de energia durante a operação.
- Eu gosto da aparência da esfera.
- Este é um projeto de engenharia interessante, em certo sentido, até um desafio. É difícil, difícil e, portanto, divertido!
Como essas esferas geodésicas são organizadas em geral? À primeira vista, parece que isso é algum tipo de entrelaçamento de arestas e é difícil capturar o sistema. Vamos tentar descobrir isso.
A base de tais estruturas é o icosaedro ou octaedro. Em geral, um poliedro regular.
No meu caso, era precisamente o icosaedro e é usado com mais frequência. Em seguida, pegamos uma face e a substituímos por vários triângulos, cujos vértices estão em uma esfera cujo centro coincide com o centro do icosaedro. Isso não parece muito bom. Vamos divagar.
Existe uma calculadora maravilhosa,
www.acidome.ru, que permite girar um inspetor em tempo real. Tome o icosaedro como base, defina a frequência como 1, parte da esfera 1/1.

Este é o nosso principal icosaedro. Frequência é quantas partes quebraremos cada extremidade do icosaedro. Definimos 3.4, 5 e nada fica claro. Alterne para o modo de teto e procure pentágonos. Nos lugares em que temos o topo do icosaedro, haverá um pentágono. Entre os três pentágonos está a face do icosaedro.

Se você observar atentamente a geodésica e souber o que procurar (geralmente um pentágono), a regularidade da estrutura se tornará visível. Na Biosfera de Montreal, com a devida diligência, é possível encontrar pentágonos e calcular a frequência. Nossa frequência é igual ao número de arestas entre dois pentágonos.
Os próprios "grandes" triângulos, com vértices no topo do icosaedro, também têm uma estrutura. Em coberturas acidome, isso é visível em cores. Os triângulos estão localizados simetricamente em relação ao centro do triângulo “grande”. O número de seus tipos é menor que o número total de triângulos. No caso de uma frequência de 5 triângulos únicos 9.

No processo de projetar uma casa, fui confrontado com a tarefa de construir uma esfera no Dynamo. Esta é uma ferramenta que permite ensinar o Autodesk Revit a trabalhar com formulários complexos. Um ambiente de programação visual.
Pesquisando, até encontrei um esboço que construía uma esfera geodésica no Dynamo. Ele construiu a esfera, mas não aquela.
Aqui está a coisa. Quando pegamos uma extremidade do icosaedro e dividimos em pequenos triângulos - isso pode ser feito de várias maneiras. No acidome, o interruptor "método de divisão" é responsável por isso.
O esboço encontrado construiu a esfera usando o método de acordes iguais. O que isso significa? Pegamos um grande triângulo do icosaedro, dividimos cada uma das suas arestas no número de partes que precisamos, conectamos os pontos nas arestas e obtemos uma grade plana de triângulos. Então projetamos essa grade na esfera. Tudo ficaria bem, mas esses triângulos em si são bem diferentes em tamanho. Central acima de tudo. É compreensível que o centro do triângulo “grande” esteja a nossa distância máxima da esfera. Isso é ruim, pois nesse caso é mais difícil otimizar o consumo de materiais. Haverá mais desperdício.
Outro método de dividir (com arcos iguais) pressupõe que construamos sobre o triângulo “grande” do arco e já os dividimos em partes iguais. A abordagem é diferente, uma simples projeção não pode fazer.
O esboço não coube. Tentei consertá-lo e, no final, tive que mergulhar nesse negócio com minha cabeça.
Como se viu, além do ambiente visual, o Dynamo incorporou o Python. Eu não encontrei esse idioma antes, mas onde nosso idioma não desapareceu? No final, é apenas uma ferramenta.
Então haverá pedaços de código, preste atenção que este é o meu mundo olá em python, e o objetivo não era criar a solução mais eficaz e eficiente, mas criar a esfera certa.
O método dos arcos iguais.
Pegamos uma das faces do icosaedro e construímos arcos a partir dos cantos deste triângulo.
for k, edge in enumerate(curves):

Em seguida, dividimos os arcos em partes iguais e conectamos os pontos nos arcos com novos arcos. Todos os arcos têm um centro - o centro da esfera. Os pontos são conectados não todos com todos, mas com o mesmo nome. Na figura, parece mais simples que no código.
for edge_index, point_list in enumerate(points): edge_arcs = [] for point_index, point in enumerate(point_list): next_edge_index = edge_index + 1 if len(points) == next_edge_index: next_edge_index = 0 end_point_index = n - point_index - 2 arc = Arc.ByCenterPointStartPointEndPoint(center_point, points[next_edge_index][end_point_index], point) if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, point, points[next_edge_index][end_point_index]) arc_points_count = n - point_index - 1; pp = Arc.PointsAtEqualSegmentLength(arc, arc_points_count) for po in pp: on_arc_points.append(po) edge_arcs.append(arc) edges_arcs.append(edge_arcs)

Opa, e os arcos não se cruzam! A pesquisa não muito fluente me levou a um livro que confirmou minhas suposições de que é necessário usar o centro de um triângulo formado pela interseção de arcos como o topo da borda da geodésica. Também fumei as fontes do acidome, mas não me lembro se encontrei confirmação lá. Lembro que foi interessante.
De alguma forma, os centros devem ser encontrados. Este é o centro do triângulo e não é difícil, mas era necessário entender onde esses triângulos estão na pilha de pontos. Pareceu-me a opção mais fácil de conectar os pontos mais próximos um do outro.
for point in on_arc_points: distance = []

Agora precisamos interconectar os pontos coletados em diferentes estágios, que são os vértices das arestas da esfera geodésica. Na imagem, esses pontos são claramente visíveis, mas quando estão na matriz - tudo é mais complicado. Havia várias opções, mas como a tarefa era obter um script de trabalho com o mínimo de esforço, isso saiu:
O segmento está pronto. Provavelmente existe algum tipo de maneira correta de resolver esse problema, mas eu preparei o meu.

Em seguida, o segmento se desdobra, é copiado várias vezes, copiado e uma esfera completa é obtida. Aqui está uma das reviravoltas:
v = Vector.ByTwoPoints(sphere_center, curves[0].StartPoint) for face_triangle in face_triangles: geodesic_sphere.append(Geometry.Rotate(face_triangle, sphere_center, v, 72))
O script saiu feio, eu o copiei algumas vezes, porque houve problemas ao exportar para o Revit. Achei que havia problemas com a construção. Como resultado, no fórum do Dynamo, o indiano levou o ucraniano e tudo deu certo!
Agora você pode construir uma esfera de qualquer frequência e diâmetro. Uma comparação de tamanhos com os resultados do acidome mostrou que tudo converge com alta precisão. A repetibilidade é boa.

Também comecei a otimizar tamanhos para minimizar a colheita. Como todos os tamanhos estavam em minhas mãos, não foi tão difícil. Como resultado, o raio da esfera ficou em 5,65 metros, com uma frequência de 5. Essas dimensões permitem usar materiais com uma largura de 125 cm com bastante eficiência.Esta largura são chapas de OSB, chapas metálicas, isolantes, drywall. Com boa otimização, o número de recortes é mínimo. Os melhores resultados podem ser alcançados calculando os layouts de triângulos no material, mas eu não fiz isso.
Além disso, era mais fácil, pois o Revit possuía uma forma complexa e permitia trabalhar com ela com o mesmo sucesso que o paralelo quadrado.
Obviamente, as dificuldades não terminaram aí, mas esta é uma história completamente diferente.