Entrevista com Will Kurt sobre seu novo livro, Bayesian Statistics - It's Great

Olá Habr!

No final do ano, conseguimos compartilhar com você a notícia de que estamos começando a trabalhar nas Estatísticas Bayesianas da maneira divertida da No Starch Press. Oferecemos uma tradução de uma entrevista detalhada com o autor do livro; o texto diz respeito ao livro em si e a tópicos relacionados e até a leitura adicional.




Eu, como a maioria dos desenvolvedores, estou imediatamente interessado em muitas coisas: programação funcional, sistemas operacionais, sistemas de tipos, sistemas distribuídos e ciência de dados. Por isso, fiquei tão inspirado ao saber que Will Kurt , autor de Get Programming with Haskell , escreveu um livro sobre estatísticas bayesianas, publicado pela No Starch Press. Não há muitas pessoas escrevendo livros sobre vários tópicos. Estou certo de que Will tem algo a compartilhar com os leitores em seu novo livro - e não ficou desapontado. O livro é um excelente material introdutório, especialmente para aqueles que não são muito bons em matemática dura, mas ainda desejam obter algo no campo da ciência de dados. Recomendo a leitura do novo livro de Kurt após o Think Stats, mas antes da Programação Probabilística de Python: Inferência Bayoriana e Algoritmos, Análise Bayesiana com Python e Análise de Dados Bayesiana.

1. Por que precisamos de outro livro sobre estatística?

Quase todos os muitos livros existentes sobre estatísticas bayesianas sugerem que o leitor já tem uma idéia geral de estatística e uma base sólida em programação. Portanto, atualmente, as estatísticas bayesianas são frequentemente percebidas como uma alternativa avançada às estatísticas clássicas (isto é, frequência). Assim, embora as estatísticas bayesianas estejam crescendo em popularidade, os materiais são projetados principalmente para pessoas que já possuem um bom treinamento quantitativo.

Quando uma pessoa decide simplesmente “estudar estatística”, ele pega um livro introdutório no qual as estatísticas são apresentadas do ponto de vista da frequência, lê-as, já descobriu um monte de testes e regras e sente que todo esse tópico é muito confuso. Eu queria escrever um livro sobre estatísticas bayesianas que qualquer pessoa pudesse pegar, ler e, depois de ler, ter uma idéia intuitiva do que é pensar estatisticamente e como resolver problemas reais com a ajuda da estatística. Não vejo razão para que as estatísticas bayesianas não possam servir como o primeiro curso introdutório neste tópico para um iniciante absoluto.

Eu ficaria muito satisfeito se algum dia com a palavra "estatísticas" as pessoas começarem a significar estatísticas bayesianas, e as estatísticas de frequência se tornarem apenas um dos nichos acadêmicos. Para isso, são necessários mais livros nos quais o conhecimento de estatísticas para um amplo círculo de leitores seja proposto usando métodos bayesianos; além disso, o autor levou em conta que esse pode ser o primeiro conhecimento de estatísticas do leitor.
Imediatamente pensei em chamar este livro de "Estatísticas da maneira divertida", mas achei que provavelmente receberia um monte de cartas raivosas de pessoas que compraram este livro para me preparar para o vestibular para estatística - e encontrei que é completamente diferente lá! Espero que meu livro seja um pequeno passo para o momento em que as estatísticas bayesianas serão solicitadas nos exames de admissão, e será aconselhável ler esse livro mesmo para aqueles que estão se preparando para o exame.

2. Qual é o público-alvo do livro? Uma pessoa pode lê-lo sem nenhuma formação matemática?

Trabalhando em “estatística bayesiana é ótimo”, tentei criar um livro, em princípio, compreensível para quem aprendeu matemática no escopo do programa de ensino médio. Mesmo que você se lembre vagamente da álgebra, o ritmo da apresentação em um livro é tal que você pode acompanhá-la. As estatísticas bayesianas exigem muito pouca análise matemática e ainda mais simplificadas com um pouco de suporte ao código de software, por isso adicionei duas aplicações ao livro que fornecem os conceitos básicos da linguagem R. Este material é suficiente para o R servir como uma calculadora avançada, e as idéias básicas da análise matemática são apresentadas em tanto que você pode descobrir todos os exemplos deste livro, onde se trata de integrais. No entanto, prometo que, para ler o livro, você não precisará resolver nenhum problema do campo da análise matemática.

Além disso, por mais que eu trabalhasse duro, tentando minimizar a quantidade de conhecimento matemático necessário para ler um livro, ao lê-lo, você começará gradualmente a aprender o modo de pensar matemático. Se você entender a matemática com a qual está operando corretamente, entenderá ainda melhor. Portanto, não tentei fugir da matemática real, mas explicá-la passo a passo, para que toda a matemática gradualmente se torne óbvia para você. Como muitos, certa vez acreditei que a matemática é uma ciência complexa e é difícil trabalhar com ela. Com o tempo, fiquei convencido de que, com a abordagem correta, a matemática não causa quase nenhuma dificuldade. Qualquer confusão na matemática geralmente surge apenas devido a tentativas de percorrer o material muito rapidamente - por isso, etapas importantes necessárias para o raciocínio adequado são perdidas.

3. Por que um programador deveria estudar teoria e estatística das probabilidades?

Eu realmente acredito que todos deveriam estudar a teoria da probabilidade e a estatística até certo ponto, pois esse conhecimento ajudará a julgar a incerteza que nos cerca em toda parte da vida. Quanto ao programador, ele definitivamente terá que lidar com algumas tarefas típicas nas quais é útil entender as estatísticas. É muito provável que, em algum momento de sua carreira profissional, você precise escrever um código no qual algumas decisões sejam tomadas com base em fatores difusos a priori. Talvez isso seja uma medida da conversão da página da web, a geração de algumas recompensas aleatórias no jogo, a distribuição aleatória de usuários em grupos ou até mesmo a leitura de informações de algum sensor difuso. Em todos esses casos, uma sólida compreensão da teoria das probabilidades o ajudará bastante. Minha própria prática mostra que a abordagem probabilística ajuda muito na depuração de muitos bugs que são difíceis de reproduzir ou rastrear para um problema complexo. Se o bug for causado por memória insuficiente, você pode ter certeza de que o bug ocorrerá com mais frequência se a memória for cortada ainda mais? Se um bug complexo puder ser explicado de duas maneiras, qual é a melhor oportunidade para explorar primeiro? Em todos esses casos, a teoria da probabilidade pode ajudar. Obviamente, o auge do aprendizado de máquina e da ciência de dados leva ao fato de que os engenheiros estão cada vez mais tendo que lidar com tarefas em que a programação oferece trabalho direto com probabilidades.

4. É possível descrever brevemente a diferença entre a freqüência e as abordagens bayesianas da teoria da probabilidade?

Na interpretação da frequência, a probabilidade é interpretada como uma afirmação sobre a frequência com que um evento deve ocorrer durante tentativas repetidas. Então, jogando uma moeda duas vezes, deve-se esperar que seja descartada uma vez pela águia, uma vez que a moeda tem dois lados e um deles tem uma águia. Na interpretação bayesiana, a probabilidade é interpretada como uma característica do nosso conhecimento, em princípio, como uma continuação da lógica. A probabilidade de jogar uma moeda com uma águia é 0,5, porque não vejo razão para que uma águia caia com mais frequência do que a coroa. Portanto, no caso de um sorteio, ambas as abordagens são totalmente funcionais. No entanto, quando se trata de chances do seu time favorito vencer a Copa do Mundo, o fator de confiança se torna muito mais significativo. A propósito, isso também significa que as estatísticas bayesianas não fazem declarações sobre o mundo, mas sobre nossa compreensão do mundo. Como todos entendem o mundo de maneira um pouco diferente, as estatísticas bayesianas nos ajudam a levar essas diferenças em consideração em nossa análise. De muitas maneiras, a análise bayesiana é a ciência da evolução das opiniões.

5. Por que o foco do livro é a abordagem bayesiana?

Existem muitas boas razões filosóficas para focar nas estatísticas bayesianas, mas fui guiado por uma razão completamente prática: com a abordagem bayesiana, tudo se torna lógico. Com base em um conjunto relativamente pequeno de regras intuitivas, você pode desenvolver uma solução para quase qualquer problema que possa encontrar. É por isso que as estatísticas bayesianas são tão poderosas e flexíveis e são fáceis de aprender. Eu acho que a maneira bayesiana de raciocinar combina exatamente com os programadores. Você não tenta resolver o problema com a ajuda de testes de improviso, mas discute isso e gradualmente chega a uma solução verdadeiramente justificada. Em princípio, estatísticas bayesianas - esse é o raciocínio. Você concorda com a análise estática apenas se ela for genuinamente lógica e convincente para você, e não porque seu teste que parece arbitrário fornece a você um valor igualmente infundado. Além disso, as estatísticas bayesianas permitem duvidar do resultado e de um ponto de vista qualitativo. Na prática cotidiana, muitas vezes acontece que duas pessoas são apresentadas com os mesmos fatos, mas suas conclusões são diferentes. As estatísticas bayesianas nos permitem modelar formalmente essa diferença de opinião, para que possamos verificar por nós mesmos quais fatos serão necessários para mudar nosso ponto de vista. Você não precisa acreditar nos resultados declarados no papel por causa de algum valor-p, acredita neles, porque eles parecem realmente convincentes.

6. Como as estatísticas bayesianas se relacionam com o aprendizado de máquina

Entre as semelhanças entre o aprendizado de máquina (em particular, as redes neurais) e as estatísticas bayesianas nas quais pensei, são as seguintes: em ambas as disciplinas, a análise matemática pode ser extremamente complicada. Em princípio, o aprendizado de máquina é o entendimento e a solução de derivativos não triviais. Você obtém uma função e, para ela, uma função de perda, calcula (automaticamente) a derivada e tenta segui-la até que ela leve aos parâmetros ideais. Muitos observam maliciosamente que a propagação para trás é apenas uma "regra em cadeia", mas em quase todas as tarefas complexas relacionadas ao aprendizado de máquina, ela é usada com muito sucesso.
A estatística bayesiana é outra faceta da análise matemática associada à resolução de integrais verdadeiramente complexas. Michael Betancourt, autor de Stan, observou perfeitamente que quase todas as análises bayesianas estão ligadas ao cálculo das expectativas, ou seja, ao cálculo das integrais. Como resultado da análise bayesiana, você ainda tem uma distribuição posterior, mas não pode usá-la de forma alguma sem integrá-la e, portanto, sem obter uma resposta concreta. Felizmente, ninguém faz comentários cruéis sobre as integrais, pois todos sabem que mesmo a integral mais trivial é bastante complicada. Aqui está como é formulado aforisticamente em um dos quadrinhos do xkcd:



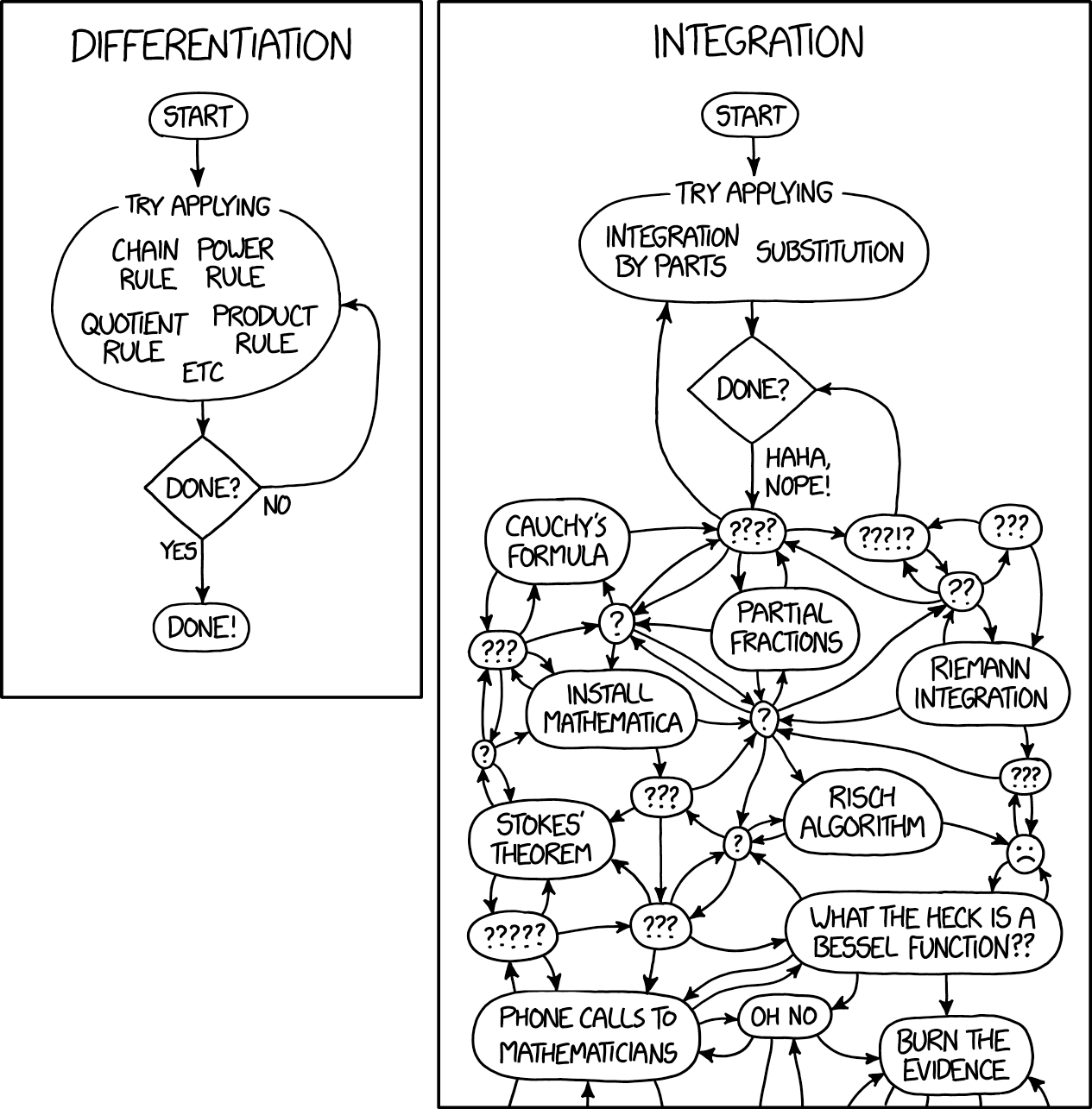
Hoje, o aprendizado de máquina e as estatísticas bayesianas estão em um estado tão estranho: desenvolvemos as idéias mais simples da análise matemática com um grau de complexidade que só se presta à computação.

Esse relacionamento também destaca um ponto-chave. Quando falamos de derivativos, procuramos um ponto específico relacionado a uma função. Portanto, se você conhece a posição e o tempo, a velocidade é um derivado que deve determinar quando você estava se movendo mais rapidamente. Um pequeno passo em direção ao progresso no MO é quando você descobre que uma única métrica é melhor do que qualquer outra pessoa. Integração é a soma de todo o processo. Novamente, se você conhece o local e a hora, a integral é a distância, e permite descobrir até onde você chegou. As estatísticas bayesianas são uma soma de tudo o que você sabe sobre um problema, mas permite não apenas fazer previsões separadas, mas também caracterizar o grau de confiança em nossas previsões, que estão em uma ampla variedade de opções. O progresso nas estatísticas bayesianas é uma compreensão de sistemas de informação cada vez mais complexos.

7. Se os leitores querem se familiarizar mais com o tópico do livro, quais materiais (livros, cursos, blogs) você os aconselha?

Tomei a máxima inspiração do livro de I. T. Jane, "Teoria da Probabilidade: a lógica da ciência". Secretamente, espero que meu livro “As estatísticas bayesianas sejam ótimas” possa se tornar um análogo de seu livro, mas destinado a uma ampla gama de leitores. Trabalhar com o livro de Janes não é uma tarefa fácil e apresenta um resultado muito radical das estatísticas bayesianas. Aubrey Clayton prestou bastante serviço a seus leitores escrevendo uma série de palestras nos capítulos deste livro.

Claro, se você gosta do livro, provavelmente vai gostar do meu blog. Recentemente, não escrevi muito lá, porque escrevi o livro “As estatísticas bayesianas são ótimas” e, antes disso, “Get Programming with Haskell”, mas agora tenho uma cabeça cheia de idéias, e nem todas são dedicadas estritamente à Bayesiana. tópicos. Como regra, reflito sobre um tópico do campo de estatística / probabilidade e, a partir dessa ideia, seleciono cuidadosamente um novo artigo para o blog.

8. Na sua experiência, qual conceito no campo da teoria / estatística das probabilidades é particularmente difícil de entender?

Honestamente, a parte mais difícil é a interpretação das probabilidades. As pessoas realmente perderam a fé em muitos analistas bayesianos, como Nate Silver (e muitos outros), quando previram que Hillary Clinton venceria as eleições de 2016 com 80% de probabilidade - e ela perdeu. As pessoas pensavam que alguém as havia enganado, e todo mundo estava errado, mas, na verdade, a probabilidade de 80% não é tanto. Se o médico me disser que minhas chances de sobrevivência são de 80%, estou seriamente nervoso.

Como regra, esse problema é resolvido da seguinte forma: indicamos as probabilidades como tais e declaramos que elas são inadequadas para expressar incerteza. Para lidar com esse inconveniente, é preciso usar coeficientes ou taxas de probabilidade ou algum tipo de sistema parecido com decibéis, como o conceito de Jane de “evidência”. No entanto, tendo pensado nas probabilidades por um longo tempo, cheguei à conclusão de que não há uma maneira única e adequada de expressar incerteza.

A essência do problema é que cada um de nós está profundamente convencido de que há certeza no mundo. Até especialistas experientes em teoria das probabilidades têm a sensação de que, se você executar a análise correta, descobrir os dados a priori necessários, adicionar outro nível ao seu modelo hierárquico, terá sucesso e se livrará da incerteza ou, pelo menos, reduzirá-a. . As probabilidades são em parte atraentes para mim por causa dessa combinação bizarra desses dois fatores: o desejo de compreender o mundo e o reconhecimento de que, não importa como você tente, o mundo o surpreenderá de qualquer maneira.

9. O que você acha dos valores-p como uma medida de significância estatística? Você poderia descrever brevemente o que é o p-hacking?

No caso dos valores-p, duas coisas são muitas vezes incompreendidas. Primeiro, uma pessoa inteligente não tentará responder perguntas com valores-p. Imagine como seria a seguinte conversa no trabalho:

Gerente: "Você corrigiu esse bug, como ele foi atribuído a você?"
Você: "Bem, tenho mais que certeza de que não consertei ..."
Gerente: “Se você o corrigiu, marque-o.”
Você: "Oh, não, não posso dizer que consertei ..."
Gerente: "Bem, você vai marcar como 'eu não vou consertar'?"
Você: "Não, não, é claro que não é nada disso"

Os valores p de muitos são confusos, pois são inerentemente obscuros. As estatísticas bayesianas indicam uma probabilidade posterior, que é uma resposta positiva a uma pergunta formulada como você deseja. No diálogo acima, o bayesiano diz: "Tenho certeza de que o bug foi corrigido". Se o gerente quiser que você responda com mais confiança, o bayesiano poderá coletar informações adicionais e dizer: "Em princípio, tenho certeza de que está consertado".

O segundo problema é o hábito arraigado de escolher 0,05 como algum tipo de significado mágico, supostamente significativo. Voltando à pergunta anterior sobre o entendimento de probabilidades, a probabilidade de 5% de um determinado evento ocorrer não significa que esse evento seja raro. Você terá 5% de chance de obter 20 pontos ao jogar dados de 20 lados. No entanto, quem já jogou Dungeons and Dragons sabe que isso está longe de ser impossível. Além dos RPGs, jogar um osso não é a melhor ferramenta para distinguir a verdade das mentiras.

Aqui chegamos ao p-hacking. Imagine que você joga Dungeons and Dragons com seus amigos e joga 20 dados de uma só vez. Então você aponta para aquele em que 20 pontos caíram e declara: "era esse osso que eu jogaria, e todo o resto eram de teste". Formalmente, você realmente marcou 20 pontos, mas isso ainda é uma farsa, você vê. Essa é a essência do p-hacking. Você faz a análise até encontrar algo "essencial" e afirma que é isso que estava procurando desde o início.

10. Recomendações finais sobre qual livro ler após o seu?

, , , , . «Bayesian Analysis with Python» (, Not Monad Tutorial). , PyMC3. , . , — “Statistical Rethinking” . , . . « – ». , «Doing Bayesian Data Analysis» .