🧒🏻 👫 🧒🏿 Problema de conclusão do n-Queens - algoritmo de solução linear 🌕 💪🏻 ⛰️

Ericgrig

Prefácio

Gostaria de começar o prefácio com palavras de gratidão a dois maravilhosos programadores de Odessa: Andrei Kiper (Lohica) e Timur Giorgadze (Luxoft), para uma verificação independente dos meus resultados, na fase inicial do estudo.

O artigo "Algoritmo linear para a solução do problema de conclusão do n-Queens" foi publicado em (arXiv.org) no início do primeiro dia de 2020. Inicialmente, o artigo foi escrito em russo; portanto, a apresentação básica é apresentada aqui e a tradução.
Essa tarefa e alguns outros conjuntos de NP-Complete (a tarefa de satisfazer as fórmulas booleanas (3-SAT), a tarefa de encontrar a camarilha máxima ou uma camarilha de um determinado tamanho ...) em momentos diferentes estavam na minha área de interesse. Eu estava procurando uma solução algorítmica baseada em vários experimentos computacionais, mas não houve sucesso concreto. Era como uma pessoa tentando aprender a ficar em forma na barra horizontal de um braço. Não há resultado, mas toda vez há uma esperança de que tudo dê certo em breve. A última vez que decidi que deveria ficar mais tempo na tarefa de Conclusão do n-Queens (como um dos membros da família) e tentar fazer alguma coisa. Aqui é apropriado relembrar a maravilhosa piada de Odessa: "Em um ônibus lotado que retorna aos subúrbios em uma estrada esburacada à noite, a voz de uma mulher é ouvida - Cara, se você me deitou completamente, faça pelo menos alguma coisa".
O estudo durou o suficiente - quase um ano e meio. Por um lado, isso se deve ao fato de que outras tarefas foram consideradas no processo de pesquisa e, por outro, houve questões difíceis ao longo do caminho, sem as quais não poderíamos avançar. Vou listar alguns deles:
- Existem n linhas na matriz de decisão, em que sequência o índice de linha deve ser selecionado se o número de possibilidades para essa escolha for n!
- quando uma linha é criada, qual das posições livres restantes nessa linha deve ser selecionada, porque o número de possibilidades para uma seleção é tão grande que pode ser considerado um "parente próximo" do infinito (por exemplo, o número de maneiras possíveis de selecionar uma posição livre em todas as linhas para um tabuleiro de xadrez de tamanho 100 x 100 é aproximadamente 10 ¹²⁴ )
- Juntos, esses dois indicadores formam um espaço de estado (um espaço de escolha). Parece que existem grandes oportunidades, você pode escolher o que deseja. Mas por trás de cada escolha específica a cada passo, há outro problema - a limitação da escolha em todos os passos subsequentes. Além disso, isso é especialmente sensível nos últimos estágios da solução do problema. Podemos dizer que a matriz de decisão é "vingativa". Todos os “erros inconscientes” que você comete ao fazer uma escolha nos estágios anteriores são “acumulados” e, no final da decisão, isso se manifesta no fato de que naquelas linhas em que você deve colocar a rainha, não há posições vazias e o ramo de busca pára. . Aqui, como Zhvanetsky: "uma jogada errada e você está grávida".
- Quando o ramo da busca por uma solução fica parado, temos a oportunidade de voltar a algumas das posições anteriores (Back Tracking), para que a partir dessa posição comecemos novamente a formar o ramo da busca por uma solução. Essa é uma "propriedade" natural de problemas não determinísticos. A questão é qual dos níveis anteriores deve ser retornado. Esse é o mesmo problema em aberto que a questão de escolher o índice de linha ou escolher uma posição livre nessa linha.
- Finalmente, um problema relacionado à velocidade do algoritmo deve ser observado. Seria triste se não houvesse objetivo de criar algoritmos de execução rápida. No processo de modelagem, não foi possível desenvolver um algoritmo que funcionasse rápida e eficientemente em todas as áreas da solução do problema. Eu tive que desenvolver três algoritmos. Eles transmitem os resultados um para o outro, como um bastão. Um deles trabalha muito rapidamente, mas de forma grosseira, o outro - pelo contrário, trabalha lenta mas eficientemente. Cada um deles trabalha na “zona de sua responsabilidade”.
Inicialmente, o objetivo do estudo era apenas encontrar pelo menos alguma solução. Eu tinha muito que descobrir antes que a primeira solução fosse desenvolvida. Demorou mais de quatro meses. Foi possível parar por aí, o objetivo foi alcançado - bem, tudo bem. Mas me pareceu que nem todas as possibilidades de uma solução algorítmica para esse problema estavam esgotadas. Naturalmente, havia um desejo de melhorar o algoritmo desenvolvido para que a complexidade do tempo fosse linear-O (n). Quando uma solução linear foi encontrada, havia “mais um desejo” - reduzir o número de casos em que o procedimento Back Tracking (BT) foi aplicado ao formar um ramo da pesquisa da solução. Era um desejo "insolente" de transferir a tarefa de não determinista para condicionalmente determinado (na medida do possível). Demorou muito tempo, mas o objetivo foi alcançado, por exemplo, no intervalo de valores do tamanho de um tabuleiro de xadrez n = (320, ..., 22500), o número de casos em que o procedimento BT nunca foi usado é superior a 50%. Acontece que em 50% dos casos, quando o programa é iniciado, o algoritmo "propositalmente" forma uma solução, nunca "tropeçando". (Lembrando o conto de fadas sobre o peixe dourado, parei com esses dois desejos ...)
Comparando as publicações com as quais me familiarizei durante a pesquisa, cheguei à conclusão de que esse problema e outros problemas desse tipo não podem ser resolvidos com base em uma abordagem matemática rigorosa, ou seja, apenas com base em definições, afirmações de lemas e provas de teoremas. Há uma "observação filosófica" sobre isso no artigo. Estou certo de que muitos problemas do NP-Complete podem ser resolvidos apenas com base na matemática algorítmica com o uso da modelagem computacional. Essa conclusão não significa limitar a matemática, pelo contrário, significa expandir as capacidades da matemática através do desenvolvimento de métodos matemáticos algorítmicos. Para cada família de problemas, você precisa usar sua própria abordagem matemática adequada. (Por que instruir um aluno de pós-graduação a resolver um problema da família NP-Complete sem aplicar matemática algorítmica e modelagem por computador, se se sabe que nada realmente resultará de tal empreendimento).
Qualquer algoritmo (programa) possui uma propriedade simples - funciona ou não! Quero apelar para os membros da nossa Comunidade Habro que têm um computador com o Matlab instalado na zona de acessibilidade. Quero pedir que você teste a operação do algoritmo considerado para resolver o problema de conclusão do n-Queens . Isso levará apenas 5 a 10 minutos. Para testar o algoritmo, você precisa seguir algumas etapas simples:
- Gere uma composição aleatória a partir de k rainhas e verifique a correção dessa composição.
- Com base no algoritmo de decisão proposto, conclua esta composição para uma solução completa. Ou o programa deve decidir que essa composição não tem solução.
- Verifique a correção da solução obtida como resultado da configuração.
Você não precisa escrever nenhum código para esse teste. Além do programa principal, preparei mais dois programas no idioma Matlab:

1. Generarion_k_Queens_Composition - geração de uma composição aleatória de tamanho k para um tabuleiro de xadrez arbitrário de tamanho nxn

2. Completion_k_Queens_Composition.m - concluir uma composição arbitrária até uma decisão completa ou decidir que essa composição não tem solução ( programa principal ).

3. Validation_n_Queens_Solution.m - verificando a correção da solução do Problema n-Queens ou a correção da composição de k rainhas.

Eles trabalham muito rápido. Por exemplo, para um tabuleiro de xadrez, cujo tamanho é de 1000 x 1000 células, o tempo total necessário para gerar uma composição arbitrária (0,0015 s.), Complete esta composição (0,0622 s.) E verifique a correção da solução obtida (0,0003 s.) não excede 0,1 segundos. (excluindo o tempo necessário para fazer o download de dados ou salvar os resultados)

Envie-me um email (ericgrig@gmail.com). Se você tiver a oportunidade de ajudar um amigo, enviarei imediatamente esses três programas. Serei grato a todos os meus colegas que podem testar objetivamente o algoritmo e expressar sua opinião na discussão.
Eu preparei o código fonte do programa, com comentários detalhados, que, espero, serão publicados em Habré em breve. Penso que aqueles que estão interessados em resolver problemas complexos da família NP-Complete encontrarão algo interessante para si.
Gostaria de apelar novamente aos membros da Comunidade Habr, mas por um motivo diferente. Aqui, em Marselha (França), a formação da equipe do France Fold Group está em andamento, cujo objetivo é a pesquisa e o desenvolvimento de algoritmos para prever as propriedades físico-químicas de compostos de alto peso molecular. Acho que não vale a pena dizer que esta é uma tarefa bastante difícil, com uma longa história, e que equipes sérias em diferentes países estão trabalhando nesse problema, incluindo a equipe Khasabis da Deep Mind (você pode ver o artigo em Habré (habr.com_Folding) . O objetivo é criar uma equipe forte que não tenha medo de resolver problemas complexos. A forma de organização do trabalho conjunto é distribuída. Cada membro da equipe vive em sua cidade e trabalha no projeto em seu tempo livre a partir de seu trabalho principal. Precisamos de programadores e pesquisadores (físicos, químicos, matemáticos, biólogos) ) etc. osto programadores “imprudentes” (ao quadrado). Escreva-me se achar interessante, o acima é o meu e-mail. Mais detalhadamente, posso dizer na carta de resposta.

O prefácio do artigo acabou sendo o mesmo do próprio artigo. O formato de apresentação da família em Habré me permite expressar meus pensamentos com mais liberdade, mas, a julgar pelo tamanho, aproveitei-o com bastante liberdade. Eu queria escrever brevemente, mas "acabou como sempre".

PS: Pensei que os membros da Comunidade Habr estariam interessados em saber quais dificuldades encontrei ao tentar publicar os resultados do estudo. Quando o artigo foi preparado, eu o reformatei no formato .tex de acordo com os requisitos do Journal of Artificial Intelligence Research (JAIR) e o enviei para lá. Costumava haver publicações sobre um tópico semelhante. Destaca-se o artigo C. Gent, I.-P. Jefferson e P. Nightingale (2017) (Complexidade da conclusão de n-rainhas) , na qual os autores provaram que o problema em questão pertence ao conjunto NP-Complete e falaram sobre as dificuldades encontradas na tentativa de resolver esse problema. Nas conclusões, os autores escrevem: “Para quem entende as regras do xadrez, o n-Queens Completion pode ser um dos problemas mais naturais de NP-Complete de todos” ( Para quem entende as regras do xadrez, a tarefa n-Queens Completion pode se tornar uma das as tarefas NP-Complete mais naturais ).

Após 10 dias, recebi uma recusa da JAIR, com a redação: "o artigo não corresponde ao formato da revista", ou seja, nem sequer levou o artigo em consideração. Eu não esperava essa resposta. Eu pensei que, se uma revista publica artigos nos quais os autores concluem que é muito difícil resolver um determinado problema e não fornece nenhuma solução concreta, o artigo que fornece um algoritmo de solução eficaz certamente será aceito para consideração. No entanto, os editores tinham sua própria opinião sobre esse assunto. (Acredito que especialistas competentes trabalhem lá, e provavelmente eles foram questionados pelo título do artigo "insolente" e tudo o que é declarado lá. Pensamos: "provavelmente há algum tipo de erro e gentilmente me mandou embora, referindo-se ao formato ").

Eu tive que escolher outra publicação científica periódica revisada por pares sobre tópicos relevantes. Aqui estou diante da dura realidade. O fato é que aproximadamente 80% de todas as revistas são pagas: ou eu tenho que pagar uma quantia decente à revista para que o artigo esteja disponível gratuitamente a todos os leitores, ou eles precisam dar o artigo como presente "na proa", e eles cobrarão a todos que quer se familiarizar com este estudo. E a primeira e a segunda opções são fundamentalmente inaceitáveis para mim. Eu me senti bem com esse método de raquete de editores quando tentei me familiarizar com algumas publicações.

A próxima revista, que professa o princípio do livre acesso à informação, foi o SMAI Journal of Computational Mathematics . Eles também recusaram com a mesma redação, embora muito mais rápido - em dois dias.

Em seguida, foi escolhida uma revista: Matemática Discreta e Ciência da Computação Teórica . Aqui os requisitos são simples, primeiro você precisa publicar o artigo em arXiv.org e somente depois registre o artigo para consideração. Ok, seguiremos as regras - enviei um artigo no arXiv.org . Eles me escreveram que publicariam o artigo em 8 horas. No entanto, isso não aconteceu após 8 horas, não após 8 dias. O artigo foi “mantido” pelos mentores e somente após 9 dias foi publicado. Não houve queixas na forma e na essência do artigo. Eu acho que, como no caso do JAIR, os mentores tinham dúvidas sobre a possibilidade de "fazer isso e escrever sobre isso". Algum tempo depois, depois de corrigir erros técnicos, o artigo foi atualizado e em sua forma final foi lançado na noite de Ano Novo.

Tenho que me debruçar sobre isso em detalhes para mostrar que, na fase de publicação dos resultados da pesquisa, pode haver problemas que não podem ser explicados logicamente.

A seguir, é apresentado um artigo cuja tradução para o inglês foi publicada em (arXiv.org) .

1. Introdução

Entre as várias opções para a formulação do problema do n-Queens, a tarefa de Conclusão do n-Queens em questão tem uma posição especial devido à sua complexidade. Em seu trabalho (Gent em tudo (2017)) mostrou que o problema de conclusão do n-Queens pertence ao conjunto NP-Complete ( mostrou que o n-Queens Completion é NP-Complete e # P-Complete ). Supõe-se que a solução para esse problema possa abrir caminho para resolvermos outros problemas do conjunto de NP-Complete .

O problema é formulado da seguinte maneira. Há uma composição de k rainhas, que são distribuídas consistentemente em um tabuleiro de xadrez de tamanho nxn . É necessário provar que esta composição pode ser completada para uma solução completa e fornecer pelo menos uma solução, ou provar que tal solução não existe. Aqui, por consistência, entendemos uma composição de k rainhas para as quais três condições do problema são atendidas: em cada linha, cada coluna e também nas diagonais esquerda e direita que passam pela célula onde a rainha está localizada, não mais que uma rainha está localizada. O problema nesta forma foi formulado pela primeira vez por Nauk (1850) .

1.1 Definições

A seguir, indicaremos o tamanho da lateral do tabuleiro de xadrez pelo símbolo n . Uma solução será chamada completa se todas as n rainhas forem consistentemente colocadas em um tabuleiro de xadrez. Todas as outras soluções, quando o número k de rainhas corretamente colocadas for menor que n - chamaremos a composição. Chamamos de positiva uma composição de k rainhas se puder ser concluída antes de uma solução completa. Por conseguinte, uma composição que não pode ser concluída até que uma solução completa seja chamada negativa. Como análogo de um "tabuleiro de xadrez" de tamanho nxn , também consideraremos uma "matriz de solução" de tamanho nxn . Como exemplo, todos os algoritmos desenvolvidos para resolver o problema serão apresentados na linguagem Matlab.

O estudo foi realizado com base em simulação computacional (simulação computacional). Para testar esta ou aquela hipótese, realizamos experimentos computacionais em uma ampla faixa de valores n = (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10000, 30.000, 50.000, 80.000, 10 ⁵ , 3 * 10 ⁵ , 5 * 10 ⁵ , 10 ⁶ , 3 * 10 ⁶ , 5 * 10 ⁶ , 10 ⁷ , 3 * 10 ⁷ , 5 * 10 ⁷ , 8 * 10 ⁷ , 10 ⁸ ) e, dependendo do valor de n , foram geradas amostras suficientemente grandes para análise. Chamamos essa lista de " lista básica de n valores " para a realização de experimentos computacionais. Todos os cálculos foram realizados em um computador comum. No momento da montagem (no início de 2013), a configuração era bem-sucedida: CPU - Intel Core i7-3820, 3,60 GH, RAM-32,0 GB, GPU- NVIDIA Ge Forse GTX 550 Ti, dispositivo de disco - ATA Intel SSD, SCSI, OS- Sistema operacional de 64 bits Windows 7 Professional . Chamamos esse kit simplesmente - desktop-13 .

2. Preparação de dados

O algoritmo começa lendo um arquivo que contém uma matriz unidimensional de dados sobre a distribuição de uma composição arbitrária de k rainhas. Supõe-se que os dados sejam preparados da seguinte maneira. Seja uma matriz zerada Q (i) = 0, i = (1, ..., n) , em que os índices das células dessa matriz correspondem aos índices de linha da matriz da solução. Se em alguma linha arbitrária i da matriz da solução houver uma rainha na posição j , a atribuição Q (i) = j é executada. Assim, o tamanho da composição k será igual ao número de células diferentes de zero da matriz Q. (Por exemplo, Q = (0, 0, 5, 0, 4, 0, 0, 3, 0, 0) significa que estamos considerando uma composição de k = 3 rainhas na matriz n = 10 , onde as rainhas estão localizadas na 3ª, 5ª e 8ª linhas, respectivamente nas posições 5, 4, 3).

3. Algoritmo para verificar a correção do problema da solução n-Queens

Para pesquisa, precisamos de um algoritmo que permita determinar a correção da solução do problema n-Queens em um curto espaço de tempo. Controlar o local das rainhas em cada linha e cada coluna é simples. A questão é sobre limites diagonais. Poderíamos construir um algoritmo eficaz para tal contabilidade se pudéssemos mapear cada célula da matriz da solução para uma determinada célula de um certo vetor de controle que caracterizaria exclusivamente a influência de restrições diagonais na célula em questão. Então, com base em se a célula do vetor de controle está livre ou ocupada, pode-se julgar se a célula correspondente da matriz de decisão está livre ou fechada.Tal idéia foi usada pela primeira vez por Sosic & Gu (1990) para levar em conta e acumular o número de situações de conflito entre diferentes posições das rainhas. Usamos uma idéia semelhante no algoritmo apresentado abaixo, mas apenas para levar em consideração se a célula da matriz da solução está livre ou ocupada. A Figura 1, como exemplo, mostra um tabuleiro de xadrez 8 x 8 acima do qual uma sequência de 24 células está localizada acima .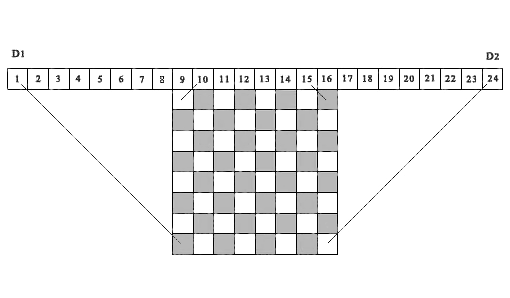

Fig. 1. Um exemplo de demonstração da correspondência das projeções diagonais das células da matriz com as células correspondentes das matrizes de controle D1 e D2 , ( n = 8)

Considere as 15 primeiras células como elementos do vetor de controle D1. As projeções de todas as diagonais esquerdas de qualquer célula da matriz da solução caem em uma das células do vetor de controle D1 . De fato, todas essas projeções estão localizadas dentro de dois segmentos de linha paralelos, um dos quais conecta a célula da matriz (8.1) à primeira célula do vetor D1 e o segundo conecta a célula da matriz (1.8) à 15ª célula do vetor de controle D1 . Nós damos uma definição semelhante para as projeções diagonais corretas. Para fazer isso, mova a origem da célula 1 para a célula 9 para a direita e considere uma sequência de 16 células como elementos do vetor de controle D2(na figura, são células dos dias 9 a 24). As projeções de todas as diagonais corretas de qualquer célula da matriz da solução cairão em uma das células desse vetor de controle, começando da 2ª à 16ª (na figura, de 10 24). Aqui, todas essas projeções estão localizadas entre dois segmentos de linhas paralelas - o segmento que conecta a célula (8,8) da matriz da solução com a célula 16 do vetor D2 (célula 24 na figura) e o segmento que conecta a célula (1,1) da matriz da solução com a célula 2 do vetor de controle D2 (célula 10 na figura). As projeções de todas as células da matriz da solução localizadas na mesma diagonal esquerda caem na mesma célula do vetor de controle esquerdo D1, respectivamente, as projeções de todas as células da matriz da solução localizadas na mesma diagonal direita caem na mesma célula do vetor de controle D2 certo . Assim, esses dois vetores de controle D1 e D2 permitem o controle total de todas as inibições diagonais para qualquer célula da matriz de decisão.

É importante notar que a idéia de usar projeções diagonais em células de vetores de controle para determinar se uma célula de uma matriz de solução com coordenadas (i, j) está livre ou ocupada também foi implementada posteriormente em Richards (1997). Ele fornece um dos algoritmos de pesquisa recursiva mais rápidos para todas as soluções, com base em operações com uma máscara de bits. Uma diferença importante é que o algoritmo indicado é projetado para a pesquisa seqüencial de todas as soluções, iniciando na primeira linha da solução da matriz para baixo ou na última linha da matriz para cima. O algoritmo que propusemos é baseado na condição de que a escolha do número de cada linha para a localização da rainha deve ser arbitrária. Para o algoritmo em consideração, isso é de fundamental importância. Observe que a figura 1 acima, construímos por analogia com o que é publicado neste artigo.
Um programa para verificar se uma determinada solução do problema n-Queens está correta ou se uma determinada composição de k é verdadeiraQueens é o seguinte.

1. Para controlar inibições diagonais, crie duas matrizes D1 (1: n2) e D2 (1: n2) , em que n2 = 2 * n e uma matriz B (1: n) para controlar a ocupação das colunas da matriz da solução. Zere essas três matrizes.

2. Introduzimos o contador do número de rainhas corretamente instaladas ( totPos = 0 ). Consistentemente, em um ciclo, a partir da primeira linha, consideramos todas as posições de rainhas fornecidas. Se Q (i)> 0 , então, com base no índice da linha i e no índice da posição da rainha nesta linha j = Q (i), formamos os índices correspondentes para as matrizes de controle D1 (r) e D2 (t) :
r = n + j - i
t = j + i

3. Se todas as condições ( D1 (r) = 0, D2 (t) = 0, B (j) = 0 ) forem satisfeitas , isso significa que a célula ( i, j) é livre e não cai na zona de projeção de restrições diagonais formadas por rainhas previamente estabelecidas. A posição da rainha nesta posição está correta. Se pelo menos uma dessas condições não for cumprida, a escolha de tal posição será errônea, respectivamente, e a decisão será errônea.

4. Se a solução estiver correta, aumente o contador do número de rainhas instaladas corretamente ( totPos = totPos + 1 ) e feche as células correspondentes das matrizes de controle: (D1 (r) = 1, D2 (t) = 1, B (j) = 1) . Então fechamos todas as células da coluna(j) e as células da matriz da solução que estão localizadas ao longo das diagonais esquerda e direita que se cruzam na célula (i, j) .

5. Repita o procedimento de verificação para todas as posições restantes.
Talvez este seja um dos algoritmos mais rápidos para avaliar a correção da solução para o problema n-Queens . O tempo de verificação de um milhão de posições para a matriz de soluções 10 ⁶ x 10 ⁶ na área de trabalho 13 é de 0,175 segundos, o que corresponde aproximadamente ao tempo de pressionar a tecla "Enter". Obviamente, esse algoritmo é linear em relação à contagem do tempo em relação a n .

4. Descrição do algoritmo para resolver o problema

O general . O problema de conclusão do n-Queens é um problema clássico não determinístico. A principal dificuldade de sua solução está relacionada à questão de escolher o índice de linha e o índice de posição nessa linha, em condições em que o espaço de estado é enorme. Ao procurar todas as soluções possíveis, esse problema não surge. Devemos considerar todas as ramificações de pesquisa válidas no espaço de estado, e a ordem em que elas são consideradas não importa. No entanto, quando uma composição arbitrária de k rainhas precisa ser concluída até uma solução completa, nesse caso, precisamos de um algoritmo para selecionar índices de linha e coluna que percebam adequadamente a composição existente e levam a uma solução mais rapidamente do que outros. Neste projeto, decidimos a questão da escolha com base na seguinte posição geral - se não pudermos formular condições que dêem preferência a qualquer linha ou posição nesta linha sobre outras, usaremos um algoritmo de seleção aleatória baseado em números aleatórios distribuídos uniformemente . Um método de seleção aleatória semelhante para resolver problemas nos quais o espaço de estados é enorme é bastante natural. Uma das edições da série Proceedings of a DIMACS Workshop (1999) foi completamente dedicada ao uso da seleção aleatória no desenvolvimento de algoritmos para resolver problemas complexos. A implementação correta do algoritmo de seleção aleatória pode ser uma solução bastante produtiva, embora essa seja uma condição necessária, mas não suficiente, para a conclusão da solução. Sosic e Gu (1990) é um dos primeiros estudos a usar um algoritmo de seleção aleatória para resolver o problema n-Queens . O algoritmo que eles examinaram é baseado em uma idéia bastante simples e concisa. Haja uma sequência de números de 1 a n , que são reorganizados aleatoriamente. Esse conjunto de números tem uma propriedade importante. Consiste no fato de que, independentemente de como esses números sejam distribuídos em diferentes linhas da matriz da solução, conforme as posições da rainha (um número por linha), as duas primeiras regras sempre serão cumpridas na declaração do problema: cada linha e cada coluna não terá mais de uma rainha. No entanto, apenas uma parte das posições assim obtidas estará livre de restrições diagonais. A outra parte estará em um estado de "conflito" com rainhas estabelecidas anteriormente. Para sair dessa situação, os autores usaram o método de comparar e trocar posições conflitantes, a fim de obter uma solução completa. Em nosso algoritmo proposto, as situações de conflito são impossíveis, pois a cada passo da solução do problema, a rainha é instalada na célula da linha em questão somente se a célula estiver livre.

4.1 Selecionando um modelo para rastreamento posterior (BT)

No processo de encontrar uma solução para um problema, uma situação pode surgir quando uma cadeia seqüencial de soluções leva a um beco sem saída. Essa é uma propriedade "genética" de problemas não determinísticos. Nesse caso, você precisa voltar para uma das etapas anteriores, restaurar o estado da tarefa de acordo com este nível e iniciar novamente a busca de uma solução a partir dessa posição. A questão é qual dos níveis anteriores deve ser retornado e quantos devem ser (por nível, queremos dizer uma certa etapa na solução do problema com um determinado número de rainhas corretamente instaladas). Obviamente, escolher um nível de solução para voltar é tão relevante quanto escolher um índice de linha ou um índice de posição nessa linha. Portanto, independentemente da abordagem para resolver esse problema, é necessário primeiro determinar o número de níveis básicos para retorno, bem como o mecanismo e as condições para retornar a um desses níveis. Em nosso algoritmo proposto, dividimos a matriz da solução em três níveis básicos. Estes são os pontos de retorno. Se, como resultado da solução, ocorrer um conflito, dependendo dos parâmetros da tarefa, retornaremos a um desses três níveis básicos. O primeiro nível base ( baseLevel1 ) corresponde ao estado em que a verificação de dados da composição em questão é concluída. Este é o começo do programa. Os valores dos dois níveis base a seguir ( baseLevel2 e baseLevel3 ) dependem do tamanho da matriz n . A dependência empírica desses valores básicos sobre o tamanho da matriz da solução foi estabelecida com base em um grande número de experimentos computacionais. Para uma representação mais precisa dessa dependência, dividimos todo o intervalo considerado de 7 a 10 ⁸ em duas partes. Seja u = log (n) , então se n <30 000 , então

baseLevel2 = n - redondo (12.749568 * u3 - 46.535838 * u2 + 120.011829 * u - 89.600272)
baseLevel3 = n - redondo (9.717958 * u3 - 46.144187 * u2 + 101.296409 * u - 50.669273)

caso contrário

baseLevel2 = n - round (-0,886344 * u3 + 56,136743 * u2 + 146,486415 * u + 227,967782)
baseLevel3 = n - redondo (14.959815 * u3 - 253.661725 * u2 + 1584.713376 * u - 3060.691342)

4.2 Estrutura do bloco

O algoritmo é construído na forma de uma sequência de cinco blocos de eventos , em que cada evento está associado à execução de uma determinada parte da solução do problema. Os algoritmos de processamento em cada bloco são diferentes um do outro. Apenas três dos cinco blocos servem para formar uma cadeia seqüencial de soluções, e os dois blocos restantes são preparatórios. A escolha do número do bloco a partir do qual os cálculos começam depende do valor de n e dos resultados da comparação do tamanho da composição k com os valores de baseLeve2 e baseLevel3 . Uma exceção é o intervalo de valores n = (7, ..., 99) , que pode ser chamado de “zona turbulenta” devido às peculiaridades do comportamento do algoritmo nesta seção. Para os valores n = (7, ..., 49) , independentemente do tamanho da composição, após inserir e monitorar os dados, os cálculos começam no 4º bloco. Para os valores n = (50, ..., 99) , dependendo do tamanho da composição, os cálculos começam no segundo bloco ou no quarto. Como mencionado acima, em cada etapa da solução do problema, apenas as posições na linha são consideradas que não se enquadram na zona de restrições criadas pelas rainhas estabelecidas anteriormente. São essas posições que são chamadas de livres .
Vamos descrever brevemente quais cálculos são realizados em cada um desses cinco blocos do programa.

4.3 Início do algoritmo

Os dados são inseridos e a composição é verificada quanto à correção. Em cada etapa de verificação, as células das matrizes de controle são alteradas. O número de rainhas instaladas corretamente é contado. Se não houver erros na composição, a solução continuará; caso contrário, uma mensagem de erro será exibida. Após a conclusão da verificação, cópias das matrizes principais são criadas para reutilização nesse nível. Depois disso, o controle é transferido para o Bloco 1 .

4.4 Bloco 1

O início da formação do ramo de pesquisa. Consideramos k rainhas localizadas em um tabuleiro de xadrez como uma posição inicial. É necessário continuar a concluir essa composição e colocar as rainhas em um tabuleiro de xadrez até que seu número total seja igual a baseLevel2 . O algoritmo usado aqui é chamado randSet & randSet . Isso se deve ao fato de que aqui estamos constantemente comparando duas listas aleatórias de índices, em busca de pares livres das restrições diagonais correspondentes. Para fazer isso, as seguintes ações são executadas:

a) duas listas são formadas: uma lista de índices de linhas livres e uma lista de índices de colunas livres;

b) reorganizar aleatoriamente números em cada uma dessas listas;

c) em um loop, cada par sucessivo de valores (i, j) , em que o índice (i) é selecionado na lista de índices de linha livre e o índice (j) na lista de índices de coluna livre, é considerado como uma possível posição rainha e é verificado se isso posição na área de projeção de exceções diagonais.

Se a regra das exceções diagonais não for violada, a posição será considerada correta e a rainha será colocada nessa posição. Depois disso, o contador é incrementado para o número de rainhas corretamente instaladas e as células correspondentes das matrizes de controle são alteradas. Se a posição (i, j) cai na zona de restrições diagonais formadas pelas rainhas estabelecidas anteriormente, nada muda e a transição para a consideração do próximo par de valores ocorre.

Quando o ciclo de comparação de todos os pares da lista é concluído, com base nos índices restantes que estão na zona de exclusão diagonal, uma lista de índices das linhas livres restantes e colunas livres é formada novamente e esse procedimento é repetido até o número total de rainhas corretamente colocadas (totPos ) não será igual ou excederá o valor limite de baseLevel2 . Quando essa condição é atendida, o controle é transferido para o Bloco 2 . Se, como resultado de uma busca por uma solução, surgisse uma situação, da lista inteira de índices das linhas e colunas livres restantes, nenhum dos pares seria adequado para a localização da rainha; nesse caso, os valores originais das matrizes de controle serão restaurados com base nas cópias geradas anteriormente , e o controle é transferido para o início do Bloco 1 para recontagem.

4.5 Bloco 2

Este bloco serve como um estágio preparatório para a transição para o Bloco 3 . Nesse nível, o número de linhas livres restantes ( freeRows ) é significativamente menor que n . Isso permite transferir eventos da matriz original de tamanho nxn para uma matriz de tamanho menor L (1: freeRows, 1: freeRows) . Além disso, com base nas informações sobre as linhas livres restantes e as colunas livres na matriz original da solução, os zeros são gravados nas células correspondentes da matriz L , indicando que essas células estão livres. Com essa transição de "projeção" , a correspondência dos índices de linha e coluna da nova matriz com os índices correspondentes da matriz original é preservada. É importante observar que, embora, no processo de solução desse problema, todos os eventos ocorram na matriz inicial de tamanho nxn , e essa matriz seja a principal arena de ação, na realidade, essa matriz não é criada e apenas controla matrizes de contabilidade para os índices de linha A (1: n) e colunas B (1: n) desta matriz.

Juntamente com a matriz L, duas matrizes de trabalho rAr (1: freeRows) e tAr (1: freeRows) também são formadas neste bloco para salvar os índices correspondentes das matrizes de controle D1 e D2 . Isso ocorre porque, quando instalamos a próxima rainha na célula (i, j) da matriz inicial de tamanho nxn , devemos excluir as células da matriz L que caem na zona de projeção das exceções diagonais da matriz "grande" original. Como o controle de restrições diagonais é realizado apenas dentro da matriz original de tamanho nxn , a presença de matrizes de trabalho rAr e tAr nos permite manter a correspondência e converter as células proibidas nos limites da matriz L. Isso simplifica bastante a contabilização de posições excluídas.
Após a conclusão do trabalho preparatório neste bloco, cópias das matrizes principais são criadas para reutilização nesse nível e o controle é transferido para o Bloco 3 .

4.6 Bloco 3

Nesse bloco, a formação do ramo de pesquisa de soluções continua com base nos dados preparados no bloco anterior. O número de linhas nas quais as rainhas estão configuradas corretamente é igual ou superior a baseLevel-2 . Você precisa continuar escolhendo até que o número de rainhas instaladas seja igual a baseLevel-3 . Aqui, usamos o algoritmo de pesquisa de soluções rand e rand , ou seja, para formar a posição de uma dama, em vez de uma lista de índices livres, apenas dois índices são usados, um valor aleatório de índice de uma linha livre e um valor aleatório de índice de uma posição livre nessa linha. Este procedimento é repetido ciclicamente até o número total de rainhas colocadas ser igual ao valor de baseLevel-3 . Assim que essa condição for atendida, o controle é transferido para o Bloco-4 . Se, como resultado dos cálculos, o ramo de pesquisa for um beco sem saída, esta seção da formação do ramo de pesquisa será fechada e retornará ao início do Bloco-3 , de onde os cálculos serão repetidos novamente. Para isso, os valores iniciais de todas as matrizes de controle são restaurados.

4.7 Bloco 4

Neste bloco, os dados são preparados para a transferência do controle para o Bloco 5 . Para esta etapa, após concluir o procedimento no Bloco 3 , o número de linhas livres ( nRow ) tornou-se ainda menor. Portanto, também é benéfico converter eventos de uma matriz maior em uma matriz menor. Essa abordagem nos dá a oportunidade de determinar rapidamente as características necessárias para as linhas restantes necessárias nesta etapa. De particular importância é o fato de que, com base nessa matriz, é possível prever as perspectivas do ramo de pesquisa para muitos passos adiante sem ter que concluir os cálculos. A condição é bastante simples. Se, entre as linhas livres restantes, houver uma linha na qual não há posição livre, o ramo de pesquisa em consideração será fechado e o controle será transferido para um dos blocos de nível inferior. As ações preparatórias realizadas aqui são muito semelhantes ao que foi feito no Bloco 2 . Com base nos índices originais de linhas livres e colunas livres, é formada uma nova matriz bidimensional, cujos valores zero correspondem a posições livres na matriz da solução original. Além disso, um array especial E (1: nRow, 1: nRow) é criado neste bloco, com base no qual você pode determinar o número de posições livres nas linhas livres restantes que serão fechadas se você selecionar a posição (i, j) para definir a rainha em matriz de origem. Antes de transferir o controle para o Bloco 5 , são executadas as seguintes ações:

a) a quantidade de vagas em todas as linhas restantes é determinada,

b) uma matriz da quantidade de posições livres, para as linhas em questão, é classificada em ordem crescente,

c) se todas as linhas livres restantes tiverem posições livres (ou seja, o valor mínimo nesta lista classificada é diferente de 0), o controle é transferido para o Bloco-5.

Se, em qualquer uma das linhas restantes, não houver posição livre, as matrizes necessárias serão restauradas com base nas cópias armazenadas e, dependendo dos parâmetros da tarefa, o controle será transferido para um dos níveis básicos.

d) cópias de backup de todas as matrizes de controle para este 4º nível são formadas.

4.8 Bloco 5

Essa etapa é final e, aqui, a formação do ramo de busca é realizada de forma mais "equilibrada" e "racional". Esta é a "última milha", resta apenas um pequeno número de linhas livres. Mas, ao mesmo tempo, esta é a parte mais difícil. Todos os erros que poderiam ter sido cometidos nos estágios anteriores da formação do ramo da busca por uma solução, no agregado, aparecem aqui - na forma da falta de uma posição vazia na linha.

O algoritmo desse bloco é executado com base em dois loops aninhados, dentro dos quais o terceiro loop é executado. Uma característica do terceiro ciclo é que ele pode ser repetido, sem alterar os parâmetros de dois ciclos externos. Isso acontece se o ramo de pesquisa gerado estiver em um impasse. O número de tais repetições não excede o valor limite de repeatBound , cujo valor ótimo foi estabelecido com base em experimentos computacionais.

O índice do loop externo está associado a uma escolha seqüencial de índices de linha que permaneceram livres após os cálculos no terceiro nível de base. Isso é feito com base em uma lista de linhas classificada anteriormente pela quantidade de posições livres na linha. A seleção começa com uma linha, com um número mínimo de posições livres e, em etapas subsequentes, em ordem crescente. Dentro deste ciclo, um segundo ciclo é formado, cujo índice itera sobre os índices de todas as posições livres na linha em questão. O objetivo do primeiro ciclo é apenas selecionar o índice de uma das linhas livres nesse nível. Consequentemente, o objetivo do segundo ciclo é apenas selecionar uma posição livre dentro da linha considerada. Essas ações ocorrem apenas no terceiro nível básico. Após essa escolha, o número de rainhas instaladas é incrementado e as células correspondentes de todas as matrizes de controle são alteradas. Além disso, o controle é transferido dentro de um ciclo aninhado (terceiro), cuja zona de atividade já é todas as demais linhas livres. Dentro deste ciclo, a escolha do índice de linha e a escolha de uma posição livre nessa linha são realizadas com base nas seguintes regras:

a) Selecione uma linha livre . Todas as linhas livres restantes são consideradas e o número de posições livres é determinado em cada linha. A linha é selecionada para a qual o número de posições livres é mínimo. Isso minimiza os riscos associados à possibilidade de excluir as últimas posições vagas em algumas das linhas restantes em que o estado é mínimo e crítico em termos do número de posições vagas ( regra de risco mínimo ). A propósito, é com essa regra que o índice do primeiro ciclo neste quinto bloco começa com uma seleção seqüencial de linhas com um valor mínimo do número de posições livres em uma linha. Se, em algum momento, as duas linhas tiverem o mesmo número mínimo de posições livres, o índice de uma das duas posições listadas primeiro na lista classificada será selecionado aleatoriamente. Se o número de linhas com o mesmo número mínimo de posições livres for maior que duas, o índice de uma das três posições listadas primeiro na lista classificada será selecionado aleatoriamente.

b) Seleção de uma posição livre consecutiva .Na lista de todas as posições vagas na linha em questão, é selecionada uma que cause danos mínimos às posições vagas em todas as linhas restantes. Isso é feito com base na matriz E. formada anteriormente. Por "dano mínimo", entendemos a escolha dessa posição em uma determinada linha que exclui a menor quantidade de posições livres em todas as linhas restantes ( regra de dano mínimo)) Se duas ou mais posições livres consecutivas tiverem os mesmos valores mínimos, de acordo com o critério de dano, o índice de uma das duas posições listadas primeiro na lista é selecionado aleatoriamente. Escolher uma posição que exclua o número mínimo de posições livres nas linhas restantes minimiza o "dano" associado à posição da rainha nesta posição. O uso dessas duas regras permite um uso mais racional dos recursos em cada etapa da formação de um ramo de pesquisa. Isso reduz bastante os riscos e aumenta a probabilidade de escolher uma composição arbitrária para uma solução completa se a composição em questão tiver uma solução. Se em alguma etapa da solução ocorrer que em uma das linhas restantes para consideração não houver vagas, esse ramo de pesquisa será fechado. Nesse caso,com base em backups, todas as matrizes de controle são restauradas e, se o número de repetições não exceder o valor limiterepeatBound, sem alterar os índices do primeiro e do segundo ciclos externos, o trabalho do terceiro ciclo aninhado é repetido novamente. Isso se deve ao fato de que, nos casos em que os valores mínimos dos critérios relevantes coincidiram, fizemos uma seleção aleatória. A reformulação do ramo de pesquisa nas mesmas condições do nível básico permite um uso mais eficiente dos "recursos iniciais" fornecidos nesse nível. O número de partidas repetidas do terceiro ciclo aninhado é limitado e, se o valor limite for excedido, a operação desse ciclo será interrompida. Depois disso, os valores das matrizes de controle são restaurados e o controle é transferido para o ciclo do terceiro nível de base para ir para o próximo valor de índice. Este procedimento é repetido ciclicamente até que uma solução completa seja obtida, ou acontece queque usamos todas as linhas livres e todas as posições livres nessas linhas neste nível básico. Nesse caso, dependendo do número total de cálculos repetidos em vários níveis de base e levando em consideração o tamanho da matriz de decisão e o tamanho da composição, retorna-se a um dos níveis mais baixos para cálculos repetidos ou se decide que a composição em questão não pode ser equipado para completar a solução. No programa, para limitar o tempo total da fatura, é aceito que o procedimentoou se for julgado que a composição em questão não pode ser concluída até uma decisão completa. No programa, para limitar o tempo total da fatura, é aceito que o procedimentoou se for julgado que a composição em questão não pode ser concluída até uma decisão completa. No programa, para limitar o tempo total da fatura, é aceito que o procedimentoO Back Tracking , independentemente de qual dos níveis anteriores o retorno é feito, pode ser executado não mais que tempos de SimSound . Esse valor limite é selecionado com base em experimentos computacionais para vários valores de n.

5. Análise da efetividade dos algoritmos de seleção

A eficiência do algoritmo randSet e randSet . Para analisar as capacidades desse algoritmo, foi realizado um experimento computacional, que consistiu em colocar rainhas na matriz da solução com base no modelo randSet e randSet , desde que exista essa possibilidade. Assim que o ramo de pesquisa alcançou um beco sem saída, ou uma solução completa foi obtida, o tamanho da composição, o tempo da solução foram fixados e o teste foi repetido novamente. Experimentos computacionais foram realizados para toda a lista básica de n valores . O número de testes repetidos para os valores n = (30, 40, ..., 90, 100, 200, 300, 500, 800, 1000) foi igual a um milhão , para os demais valores, o número de testes, com aumento de n, diminuiu gradualmente de 100000 para 100. Uma análise dos resultados de experimentos computacionais permite tirar as seguintes conclusões:

a) Como resultado de apenas o primeiro ciclo do procedimento randSet & randSet, em média cerca de 60% de todas as rainhas são colocadas corretamente. Para n = 100, o número de rainhas colocadas corretamente é 60,05%. Com um aumento no valor de n, esse valor diminui gradualmente e para n = 10 ⁷ equivale a 59,97%.

b) O histograma da distribuição dos valores de comprimento das composições obtidas tem a mesma forma, independentemente do tamanho da matriz de decisão n. Além disso, todos eles têm uma característica - o lado esquerdo da distribuição (para o valor modal) difere do lado direito. Na Figura 2, como exemplo, o histograma correspondente para a

Fig. 2. Um histograma da distribuição de soluções de vários comprimentos para o modelo randSet e randSet ( n = 100, tamanho da amostra = 10 ⁶ ).

n = 100. Parece que o histograma é coletado da distribuição de frequência de dois eventos diferentes, uma vez que a frequência de ocorrência de eventos nas partes esquerda e direita da distribuição é diferente. Para descrever essa distribuição, é mais provável usar duas funções da densidade da distribuição normal, uma das quais cobre o intervalo para o valor modal, a outra - o intervalo após o valor modal.

c) O valor médio do número de rainhas ( qMean ) que pode ser definido na matriz de decisão com base nesse algoritmo aumenta com n . Como pode ser visto na Figura 3, onde é apresentado um gráfico da dependência da razão qMean / n no tamanho da matriz n , essa proporção aumenta com o aumento do tamanho da matriz. Por exemplo

Fig. 3. A dependência da razão qMean / n no valor de n para vários tamanhos da matriz da solução. O modelo é randSet e randSet , qMean é o valor médio do comprimento da solução.

se, para uma matriz 100x100 , o algoritmo de seleção de posição randSet & randSet permite que "sem parar" coloque rainhas em média 89 linhas; em uma matriz 1000x1000 , o número dessas linhas aumenta em média para 967.

d) Com base no algoritmo randSet & randSet, você pode obter o valor completo Como solução, no entanto, a "produtividade" dessa abordagem é extremamente baixa. Como pode ser visto na Figura 4, para

Fig. 4. A diminuição da probabilidade de obter uma solução completa no modelo randSet e randSet com um aumento em n .

valores de n = 7, a probabilidade de obter uma solução completa é 0,057 . Além disso, com um aumento em n, a probabilidade de obter uma solução completa diminui rapidamente, aproximando-se assintoticamente de zero. A partir do valor n = 48, a probabilidade de obter uma solução completa é da ordem de 10 ^-6 . Após o valor limite n = 70, para os valores subsequentes de n, nenhuma solução completa foi obtida (com o número de testes igual a um milhão ).

e) ModeloOs formulários randSet e randSet pesquisam ramos a uma velocidade muito alta. Para n = 1000, o tempo médio para obter a composição é de 0,0015 segundos. O comprimento médio das composições é 967. Portanto, para n = 10 ^{6, o} tempo médio é de 2.6754 segundos, com um comprimento médio de composições de 999793.

f) Exceto por um pequeno intervalo n <= 70, quando o modelo randSet & randSet em casos muito raros pode levar a solução completa, em todos os outros casos, o ramo de decisão termina com a formação de uma composição negativa, que não pode ser concluída até uma solução completa. Portanto, o algoritmo randSet e randSetEle tem uma vantagem importante - a alta velocidade de formação do ramo de pesquisa e uma desvantagem significativa é que, se o tamanho da composição exceder um determinado valor limite, esse algoritmo leva à formação de composições que não podem ser concluídas até uma solução completa. Para superar essa desvantagem, paramos a formação do ramo de pesquisa quando o limite baseLevel-2 é atingido .

A eficiência do algoritmo rand & rand . Para determinar as capacidades do algoritmo rand & rand , foi realizada uma simulação de computador bastante detalhada para uma lista básica de n valores . Tal como no modelo randSet e randSet, o número de retestes na maioria dos casos foi igual a um milhão . Para outros valores, o número de testes diminuiu gradualmente de 100.000 para 100.

Ambos os algoritmos são baseados no princípio da seleção aleatória. Portanto, é de esperar que as conclusões aqui tiradas sejam basicamente idênticas às conclusões formuladas para o modelo randSet e randSet . No entanto, existe uma diferença fundamental entre eles e consiste no seguinte:

a) o modelo rand & rand não funciona tão "duro" quanto o modelo randSet & randSet . Se falarmos sobre algum "índice de uso racional das oportunidades oferecidas", o modelo rand & randa cada passo usa os recursos de maneira mais racional. Isso leva ao fato de que, por exemplo, em n = 30, a probabilidade de obter uma solução completa de 0,00170 nesse modelo é 15 vezes maior que o valor semelhante de 0,00011 para o modelo randSet e randSet . Além disso, aqui, até o valor limite n = 370, permanece a probabilidade de obter pelo menos uma solução completa durante um milhão de testes. Após esse valor limite, para valores subsequentes de n com o número de testes igual a um milhão, nenhuma solução completa foi obtida com base no modelo rand & rand .

b) esse algoritmo é muito mais lento que o algoritmo randSet & randSet . Se porn = 1000 para gerar uma composição de tamanho 967, o tempo médio para obter uma composição será de 0,0497 segundos, 33 a mais do que o valor correspondente de 0,0015 para o modelo randSet & randSet .

A razão para as diferenças entre dois métodos essencialmente semelhantes de seleção aleatória se deve ao fato de que, no modelo randSet e randSet , para acelerar os cálculos, a seleção aleatória da lista restante não é realizada em cada etapa. Em vez disso, um par de índices é selecionado sequencialmente em duas listas, cujos elementos foram reorganizados aleatoriamente. Essa seleção não é aleatória em toda a extensão; no entanto, ela se ajusta bem à lógica do problema e permite que você conte rapidamente.

Para demonstrar visualmente a operação do algoritmo rand & rand, foi realizada a seguinte experiência:

a) Para um tabuleiro de xadrez de tamanho 100x100, após cada etapa da localização da rainha em qualquer linha, foi determinado o número de posições livres em cada uma das linhas livres restantes. Assim, após cada etapa da solução do problema, recebemos uma lista de linhas livres e uma lista correspondente do número de posições livres nessas linhas. Isso possibilitou a construção de um gráfico no qual os índices das colunas da matriz em questão são plotados ao longo do eixo das abcissas e o número de posições livres restantes ao longo do eixo das ordenadas. Para comparação, os cálculos também foram realizados para o modelo de seleção seqüencial de posições. Por seleção sequencial entende-se o seguinte. A primeira linha é considerada, na qual a primeira posição livre na lista é selecionada. Então, a segunda linha é considerada, na qual a primeira posição livre na lista, etc. também é selecionada. Nas figuras 5 e 6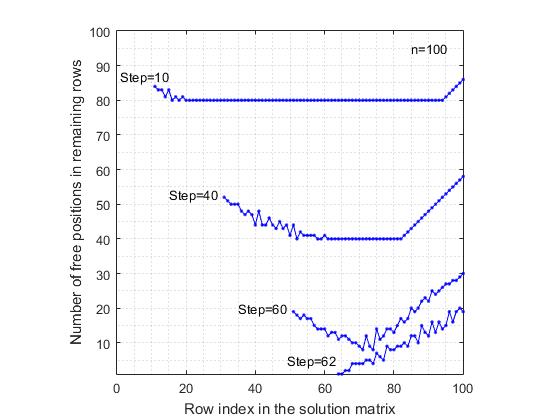

Fig. 5. Reduzir o número de posições livres nas linhas livres restantes após a colocação das rainhas. Seleção seqüencial regular de posições.

Os resultados que correspondem aos modelos em consideração são apresentados. Para maior clareza, o gráfico mostra os resultados somente após as etapas (10, 40, 60). Para o modelo de seleção sequencial de posições, o último é o gráfico após a 62ª etapa, pois o ramo de pesquisa termina devido à falta de uma posição livre na 63ª linha. Por outro lado, no modelo rand & rand , o último gráfico é apresentado após o 70º passo da colocação da rainha, embora aqui, o número médio de rainhas corretamente posicionadas atinja 89, o que é 26 passos a mais do que no modelo seqüencial. Uma visão estranha dos gráficos no modelo rand & randdevido ao fato de o índice de linha ser selecionado aleatoriamente entre as linhas livres restantes e, portanto, eles estão espalhados aleatoriamente por toda a matriz da solução. Uma comparação dessas duas figuras mostra que no modelo seqüencial de seleção de posição, a faixa de variabilidade do número de posições livres é maior do que no modelo rand & rand . Isso se deve ao fato de que, com a seleção regular, restrições diagonais excluem de maneira não uniforme as posições livres nas linhas restantes, o que leva ao fato de que em algumas linhas a taxa de redução no número de posições vagas é maior do que em outras linhas.

Fig. 6. Reduzir o número de posições livres nas linhas livres restantes após a colocação das rainhas. O modelo de posicionamento é rand & rand .

Por outro lado, com a seleção aleatória do índice de linha livre e do índice de coluna livre, as posições da rainha são distribuídas igualmente sobre a "área" da matriz de decisão, o que reduz a taxa "média" de redução no número de posições livres nas linhas restantes. Assim, levando em consideração os recursos do algoritmo rand & rand , nós o usamos no programa para continuar a formação do ramo de pesquisa de soluções até que o nível baseLevel-3 seja atingido .

Deve-se notar que, mesmo que os algoritmos de seleção ( randSet e randSet, rand e rand ) não fossem tão eficientes, ainda teríamos que usar outro método de seleção aleatória ao desenvolver o algoritmo. Isto é devido à própria declaração do problema.Problema de conclusão do n-Queens . Se imaginarmos que existe um certo algoritmo ideal que resolve o problema, na entrada, esse algoritmo sempre receberá um determinado conjunto aleatório de índices de linha e coluna. Cada vez será um novo conjunto aleatório de índices de linhas e colunas, com uma enorme variedade de possibilidades. Para poder “absorver” o algoritmo de uma variedade de composições aleatórias, o próprio algoritmo deve ser construído com base na seleção aleatória. A correspondência deve ser como uma chave da fechadura . Se construirmos o algoritmo com base neste princípio, qualquer composição consistente de krainhas serão consideradas como a posição inicial (inicial) no ciclo de tomada de decisão. Além disso, o objetivo será apenas continuar a formação do ramo da busca de uma solução até que uma solução seja encontrada para uma determinada composição ou seja provado que essa solução não existe.

6. Um exemplo de uso da regra de risco mínimo (n = 100)

No estágio inicial de localização de uma solução, quando o número de posições livres nas linhas não é crítico, a escolha do índice da linha livre ou o índice da posição nessa linha não é fatal. No entanto, no último estágio, quando o número de posições livres em algumas linhas é 1 ou 2, nesse caso, você deve escolher um algoritmo de seleção diferente. Nesse nível, os algoritmos de seleção aleatória randSet & randSet e rand & rand não funcionarão mais.

A razão pela qual os algoritmos de seleção aleatória não funcionarão pode ser explicada pelo seguinte exemplo simples. Vamos, em algum momento da solução do problema, para um valor arbitrário de n, nas linhas restantes i ₁ , i ₂ , ..., i _ko número de posições vagas (indicado entre parênteses) é: i ₁ (1), i ₂ (2), i ₃ (4), i ₄ (5), i ₅ (3), i ₆ (4) etc. Se selecionarmos aleatoriamente qualquer linha, mas não a linha i ₁ , na qual existe apenas uma posição livre, isso pode levar a uma situação de risco quando proibições diagonais relacionadas à posição da rainha na linha selecionada podem levar ao fechamento da única posição livre na linha i ₁ , o que levará a solução a uma parada. De todas as linhas i ₁ , i ₂ , ..., i _ko mais vulnerável e sensível à escolha do índice de linha é a linha i ₁ . Nessas situações, você deve primeiro selecionar a linha cujo status é o mais crítico e criar um risco para resolver o problema. Portanto, na última etapa da solução do problema, em cada etapa é necessário escolher a posição da linha com base em um algoritmo simples de risco mínimo.

Para maior clareza, consideremos, por exemplo, uma matriz 100 x 100 , o último estágio na formação de uma solução real, após o 88º passo. Até a conclusão da tarefa, restavam 12 linhas livres, para cada uma das quais o número de posições livres foi encontrado (as linhas são classificadas em ordem crescente do número de posições livres):Etapa 89 - 25 (1), 12 (2), 22 (2), 82 (2), 88 (2), 7 (3), 64 (3), 3 (4), 76 (4), 91 (4), 4 (5), 96 (5) - indica o índice de uma linha livre e, entre parênteses, o número de posições livres nessa linha. De acordo com a regra de risco mínimo, na 89ª etapa da solução do problema, a linha 25 é selecionada e a posição livre que está nela. Como resultado da recontagem, temos 11 linhas livres restantes: Etapa-90 - 7 (2), 12 (2), 22 (2), 82 (2), 88 (2), 3 (3), 64 (3), 76 (3), 4 (4), 91 (4), 96 (4).Como você pode ver, o número de posições livres nas cinco primeiras linhas é igual e igual a 2. Portanto, o índice de uma das três primeiras linhas é selecionado aleatoriamente. Nesse caso, a 12ª linha foi selecionada e a posição dos dois restantes nessa linha, o que leva a danos mínimos. Assim, na 91ª etapa da formação da solução, temos 10 linhas livres: Etapa-91 - 22 (1), 3 (2), 7 (2), 82 (2), 88 (2), 64 (3) 76 (3), 91 (3), 4 (4), 96 (4) . Nesta etapa, a linha 22 é selecionada e aquela posição livre que está nela. Continuando de maneira semelhante, foi formada a seguinte sequência de decisões (Tabela 1). Os índices das linhas selecionadas são mostrados em negrito.

**Tabela 1. Demonstração do uso da regra de risco mínimo ( n = 100).**
Etapa	linha	linha	linha	linha	linha	linha	linha	linha	linha	linha	linha
89	25 (1)	12 (2)	22 (2)	82 (2)	7 (3)	64(3)	3(4)	76(4)	91(4)	4(5)	96(5)
90	7(2)	12(2)	22(2)	82(2)	3(3)	64(3)	76(3)	4(4)	91(4)	96(4)
91	22(1)	3(2)	7(2)	82(2)	64(3)	76(3)	91(3)	4(4)	96(4)
92	88(1)	3(2)	7(2)	82(2)	91(2)	64(3)	76(3)	4(4)	96(4)
93	3(1)	7(2)	76(2)	82(2)	91(2)	4(3)	64(3)	96(4)
94	76(1)	4(2)	7(2)	82(2)	91(2)	64(3)	96(4)
95	91(1)	7(2)	82(2)	64(3)	96(3)
96	4(1)	82(1)	7(2)	64(3)	96(3)
97	7(1)	82(1)	64(2)	96(3)
98	82(1)	64(2)	96(2)
99	64(1)	96(1)
100	64(1)

Neste exemplo em particular, em 11 dos 12 casos, houve uma situação em que na lista de linhas livres restantes havia pelo menos uma linha na qual apenas uma posição livre permaneceu. Se não usássemos a regra de risco mínimo, não conseguiríamos chegar ao fim. Como um “movimento errado” na escolha de um índice de uma linha livre, provavelmente levaria à destruição da única posição livre que estava em uma das linhas livres restantes. É por isso que, ao usar apenas o algoritmo randSet x randSet ou rand x rand para obter uma solução completa, nos últimos estágios, a solução chega a um beco sem saída.
Deve-se notar que o algoritmo de risco mínimo tem um significado cotidiano simples e é frequentemente usado na tomada de decisões. Por exemplo, o médico trabalha primeiro no paciente cuja condição é mais crítica para a vida, da mesma forma, o fazendeiro, durante uma seca severa, tentando salvar a colheita, primeiro regou as áreas que estão na condição mais crítica ...

7. Análise da eficiência do algoritmo

Para avaliar a eficiência do algoritmo para vários valores de n, foi realizado um experimento computacional bastante longo (em termos de tempo total). Inicialmente, um algoritmo bastante rápido foi desenvolvido para gerar matrizes de soluções nQueens Problem para um valor arbitrário de n. Em seguida, com base nesse programa, grandes amostras de soluções foram formadas para uma lista básica de n valores. Os tamanhos das amostras obtidas das soluções nQueens Problem para vários valores de n, respectivamente, foram iguais: (10) - 1000, (20, 30, ..., 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10,000) - -10000, (30000, 50000, 80000) - 5000, (105, 3 * 105) - 3000, (5 * 105, 8 * 105, 106) - 1000, (3 * 106) - 300, ( 5 * 106) - 200, (10 * 106) - 100, (30 * 106) - 50, (50 * 106) - 30, (80 * 106, 100 * 106) - 20. Aqui, entre parênteses, é indicada uma lista de n valores e um traço duplo indica o tamanho da amostra das soluções obtidas.Depois disso, composições aleatórias de tamanho arbitrário foram formadas com base em cada amostra de soluções. Por exemplo, para cada uma das 10.000 soluções para n = 1000, foram formadas 100 composições aleatórias de tamanho arbitrário. O resultado foi uma amostra de um milhão de músicas. Como qualquer composição de tamanho arbitrário, formada com base em uma solução existente, pode ser concluída pelo menos uma vez até uma solução completa, a tarefa era concluir cada composição da amostra gerada para uma solução completa com base no algoritmo da solução n-Queens Completion Problem . Como no algoritmo considerado em cada etapa é verificada a colocação correta da rainha no tabuleiro, aqui, em princípio, elas não podem sercom base em cada amostra de soluções, foram formadas composições aleatórias de tamanho arbitrário. Por exemplo, para cada uma das 10.000 soluções para n = 1000, foram formadas 100 composições aleatórias de tamanho arbitrário. O resultado foi uma amostra de um milhão de músicas. Como qualquer composição de tamanho arbitrário, formada com base em uma solução existente, pode ser concluída pelo menos uma vez até uma solução completa, a tarefa era concluir cada composição da amostra gerada para uma solução completa com base no algoritmo da solução n-Queens Completion Problem . Como no algoritmo considerado em cada etapa é verificada a colocação correta da rainha no tabuleiro, aqui, em princípio, elas não podem sercomposições aleatórias de tamanho arbitrário foram formadas com base em cada amostra de soluções. Por exemplo, para cada uma das 10.000 soluções para n = 1000, foram formadas 100 composições aleatórias de tamanho arbitrário. O resultado foi uma amostra de um milhão de músicas. Como qualquer composição de tamanho arbitrário, formada com base em uma solução existente, pode ser concluída pelo menos uma vez até uma solução completa, a tarefa era concluir cada composição da amostra gerada para uma solução completa com base no algoritmo da solução n-Queens Completion Problem . Como no algoritmo considerado em cada etapa é verificada a colocação correta da rainha no tabuleiro de xadrez, aqui, em princípio, elas não podem serForam formadas 100 composições aleatórias de tamanho arbitrário. O resultado foi uma amostra de um milhão de músicas. Como qualquer composição de tamanho arbitrário, formada com base em uma solução existente, pode ser concluída pelo menos uma vez até uma solução completa, a tarefa era concluir cada composição da amostra gerada para uma solução completa com base no algoritmo da solução n-Queens Completion Problem . Como no algoritmo considerado em cada etapa é verificada a correta colocação da rainha no tabuleiro de xadrez, aqui, em princípio, elas não podem serForam formadas 100 composições aleatórias de tamanho arbitrário. O resultado foi uma amostra de um milhão de músicas. Como qualquer composição de tamanho arbitrário, formada com base em uma solução existente, pode ser concluída pelo menos uma vez até uma solução completa, a tarefa era concluir cada composição da amostra gerada para uma solução completa com base no algoritmo da solução n-Queens Completion Problem . Como no algoritmo considerado em cada etapa é verificada a correta colocação da rainha no tabuleiro de xadrez, aqui, em princípio, elas não podem sera tarefa era concluir cada composição da amostra gerada, com base no algoritmo da solução n-Queens Completion Problem, para uma solução completa. Como no algoritmo considerado em cada etapa é verificada a colocação correta da rainha no tabuleiro, aqui, em princípio, elas não podem sera tarefa era concluir cada composição da amostra gerada para uma solução completa, com base no algoritmo da solução n-Queens Completion Problem. Como no algoritmo considerado em cada etapa é verificada a correta colocação da rainha no tabuleiro de xadrez, aqui, em princípio, elas não podem serDecisões de falso positivo (ou seja, decisões incorretas que consideramos erradas). No entanto, pode haver soluções de falsos negativos - no caso de qualquer composição formada com base na solução existente não ser concluída pelo programa até que a solução seja concluída (embora saibamos que todas as composições têm uma solução). Realizando um experimento computacional em uma gama tão ampla de n valores, estabelecemos os seguintes objetivos:

a) determinar a complexidade de tempo do algoritmo,

b) determinar a probabilidade de soluções de falso-negativos para vários valores de n,

c) determinar a frequência com que o procedimento de Back Tracking é usado para valores diferentes de n.

Os resultados desse experimento computacional são apresentados na tabela 2.

**2. n.**
n – ; m – ; t _mean , t _min , t _max – , ; t90 _mean – , 10% ; FalseNeg( FalseNegative) – , ; *t _row = t _mean *10 ⁶ / n* , 10 ⁶ , *nxn* .
n	m	t _mean	t90 _mean	t _min	t _max	FalseNeg	t _row
10	5000	0.001010	0.000532	0.000168	0.080673	2	1.0102
20	10 ⁵	0.003589	0.001809	0.000197	0.363096	5	1.7945
30	10 ⁵	0.008025	0.003793	0.000244	0.495716	10	2.6752
40.	10 ⁵	0.014323	0.009127	0.000252	0.965817	7	3.5807
50.	10 ⁵	0.005357	0.003589	0.000313	0.441711	9	10.7146
60	10 ⁵	0.005991	0.004103	0.000340	0.013738	10	9.9852
70	10 ⁵	0.006533	0.004566	0.000368	0.583897	8	9.3328
80	10 ⁵	0.006975	0.004987	0.000394	0.635676	7	8.7187
90	10 ⁵	0.006912	0.004763	0.000393	1.012710	4	7.6840
100	10 ⁵	0.007264	0.005107	0.000419	0.692387	4	7.2641
300	10 ⁵	0.013518	0.009496	0.000986	3.349766	3	4.5060
500	10 ⁵	0.028194	0.014554	0.001541	4.558749	2	5.6388
800	10 ⁵	0.049385	0.022735	0.002367	6.192782	1	6.1731
1000	10 ⁶	0.062157	0.027727	0.002943	8.015123	0 0	6.2156
3000	10 ⁵	0.177290	0.088507	0.008537	16.713140	0 0	5.9097
5000	10 ⁵	0.159239	0.136047	0.014224	42.181080	0 0	3.1849
10 ⁴	10 ⁵	0.321003	0.270927	0.028594	79.321174	0 0	3.2100
3*10 ⁴	10 ⁴	0.968795	0.651618	0.084936	139.28827	0 0	3.2293
5*10 ⁴	5000	1.147196	0.864045	0.143005	154.38225	0 0	2.2944
8*10 ⁴	4000	2.112079	1.215612	0.229532	204.27321	0 0	2.6401
10 ⁵	2000	2.253118	1.433197	0.290566	224.34623	0 0	2.2531
3*10 ⁵	2000	4.330649	3.181905	0.990932	340.29584	0 0	1.4435
5*10 ⁵	2000	5.985339	4.532205	1.488209	382.20016	0 0	1.1971
8*10 ⁵	2000	8.297512	6.554302	2.902425	75.87513	0 0	1.0372
10 ⁶	1000	11.376632	7.932194	2.954968	510.6265	0 0	1.1377
3*10 ⁶	400	23.138609	18.521503	10.433580	122.7597	0 0	0.7713
5*10 ⁶	300	33.103386	28.057816	14.937556	155.0890	0 0	0.6621
10*10 ⁶	200	61.444001	52.269241	31.624475	228.3087	0 0	0.6144
30*10 ⁶	50.	149.71717	136.66441	84.556686	352.0534	0 0	0.4991
50*10 ⁶	40.	253.86220	228.93732	105.37934	558.4629	0 0	0.5077
80*10 ⁶	30	372.29294	341.56397	250.80182	728.4806	0 0	0.4654
100*10 ⁶	20	508.43573	474.04890	354.80864	831.3753	0 0	0.5084

A conclusão geral que pode ser tirada com base nos resultados obtidos é a seguinte:

a) O algoritmo funciona com rapidez suficiente. Por exemplo, o tempo médio de compilação de uma composição arbitrária para um tabuleiro de xadrez de tamanho 1000 x 1000 , obtido com base em um milhão de experiências de computação, é de 0,062157 segundos. Isso significa que, se a composição tiver uma solução, ela será encontrada imediatamente após pressionar a tecla "Enter" . O tempo médio de compilação de uma composição arbitrária, para todos os valores de n , na faixa de 7 a 30.000, não excede um segundo.

b) Em cada amostra, existem aproximadamente 10% das composições, que requerem muito mais tempo para serem concluídas. Tais composições formam uma longa cauda direita no histograma de distribuição. Se excluirmos esses 10% das composições e realizarmos cálculos para os 90% restantes das soluções, o tempo de cálculo ( _média t90 ) será muito menor. Por exemplo, para um tabuleiro de xadrez 1000 x 1000 , o tempo médio de contagem será de 0,027727 segundos, 2,24 vezes menor que o tempo médio obtido em toda a amostra.

c) Para valores n≤800 , na amostra de composições havia aquelas que não podiam ser concluídas até uma solução completa. Isso é falso negativodecisões. Dentro dos limites especificados no programa, permitindo que o procedimento de Back Tracking seja executado até 1000 vezes, o algoritmo falhou ao concluir essas composições. Eles foram erroneamente classificados como composições negativas, ou seja, aqueles que não têm uma solução. O número dessas soluções de falso negativo é insignificante e sua participação na amostra é menor que 0,0001. Além disso, à medida que n aumenta , a proporção de soluções de falso negativo diminui. Para todos os valores de n > 800, nesta série de experimentos computacionais, não houve um único caso de soluções de falso negativo . No entanto, é óbvio que, se o tamanho da amostra aumentar muitas vezes, a possibilidade do aparecimento de Falso Negativo não é excluída.soluções, embora a probabilidade de tal evento seja um número muito pequeno.

A complexidade do tempo do algoritmo . A Figura 7 mostra um gráfico de alterações no tempo médio de separação de composições aleatórias para vários valores de n .

Fig. 7. A dependência do tempo médio de colheita ( t ) de composições aleatórias sobre o tamanho ( n ) da matriz de decisão.

O logaritmo decimal do valor de n é plotado no eixo das abcissas , e o logaritmo, aumentado em 1000 vezes, do tempo médio de contagem, é plotado no eixo das ordenadas. Para maior clareza, a figura também mostra a linha pontilhada da diagonal do quadrante. Pode-se observar que o tempo de separação aumenta linearmente com o aumento de n. Em toda a faixa de n de 50 a 10 ⁸os valores experimentais do tempo de contagem formam uma linha reta, que com uma correlação razoavelmente alta ( R = 0,9998 ) é descrita pelo

log da equação de regressão linear (1000 * t) = - 0,628927 + 0,781568 * log (n)

Um pequeno desvio da tendência geral é típico apenas para os valores n = ( 10, ... 49) , devido ao fato de que apenas o quinto bloco de cálculos é usado nessa faixa para resolver o problema, cujo algoritmo difere significativamente da operação dos algoritmos do primeiro e terceiro blocos. Na dependência resultante, o coeficiente linear ( 0,781568) é menor que a unidade, o que leva ao fato de que, com o aumento do valor de n, a linha de regressão e a diagonal do quadrante divergem. Para explicar claramente o motivo dessa discrepância em vez do tempo inicial, consideramos o tempo médio necessário para a localização de uma rainha em uma linha, ou seja, divida o tempo médio de contagem por n . Chamamos esse indicador de tempo reduzido . Obviamente, se o tempo reduzido não mudar com o aumento de n , essa solução será linear ( O (n) ). Como pode ser visto na Figura 8, onde uma representação gráfica do logaritmo do tempo dada,

Fig. 8 Dependência de tempo médio ( _linha t), necessário para que a rainha esteja localizada em uma linha arbitrária, a partir do tamanho ( n ) da matriz da solução.

( tRow ), aumentado em 10 ⁶ vezes, a partir do logaritmo do tamanho da matriz da solução, na faixa de n de 50 a 10 ⁸ , o tempo reduzido diminui com o aumento de n . Se o tempo reduzido para n = 50 for 10,7146 * 10 ^-6 segundos, o tempo correspondente para n = 10 ^{8 será} reduzido em 21 vezes e será 0,5084 * 10 ^-6segundos. Esse comportamento do algoritmo, à primeira vista, parece errôneo, pois não há razões objetivas pelas quais o algoritmo o considerará mais lento para valores pequenos de n do que para valores grandes. No entanto, não há erro, e essa é uma propriedade objetiva desse algoritmo. Isso se deve ao fato de que esse algoritmo é uma composição de três algoritmos que operam em velocidades diferentes. Além disso, o número de linhas processadas por cada um desses algoritmos muda com o aumento do valor de n. É por esse motivo que o tempo de contagem está aumentando no intervalo inicial de valores n = (10, 20, 30, 40), uma vez que todos os cálculos nessa pequena área são realizados apenas com base no quinto bloco de procedimentos, que funciona de maneira muito eficiente, mas não tão rápida quanto. primeiro bloco de procedimentos. Assim, dado que o tempo de contagem necessário para posicionar a rainha em uma linha,diminui com o aumento do tamanho do tabuleiro de xadrez, a complexidade do tempo desse algoritmo pode ser chamada de decrescente - linear.

O número de vezes que o Back Tracking (BT) foi usado . Em todos os casos de um experimento computacional, rastreamos o número de casos usando o procedimento BT na resolução de cada problema. Foi feito um somatório cumulativo de todos os casos de uso de BT, independentemente do nível de base retornado no processo de busca de uma solução. Isso nos deu a oportunidade de determinar, para cada amostra, a proporção daquelas decisões nas quais o procedimento BT nunca foi usado. A Figura 9 mostra a

Fig. 9. A proporção de decisões na amostra em que o procedimento de Back Tracking nunca foi usado em um

gráfico que mostra como a proporção de casos da solução muda sem usar o procedimento BT ( Zero Back Tracking ) com aumento de n. Pode-se observar que no intervalo de valores n = (7, ..., 100000) , o número de soluções nas quais o procedimento BT nunca foi usado excede 35%. Além disso, no intervalo de valores n = (320, ..., 22500) , o número de tais casos excede 50%. Os resultados mais efetivos foram obtidos para um tabuleiro de xadrez de tamanho 5000 x 5000 , onde, em uma amostra de 10.000 composições, em 61,92% dos casos foi realizada a solução “determinística” do problema não determinístico , porque Procedimento BT a 61,92%casos nunca foram usados. Nas demais soluções, em 21,87% dos casos, o procedimento BT foi utilizado 1 vez, em 9,07% dos casos - 2 vezes e em 3,77% dos casos - 3 vezes. Juntos, isso representa 96,63% dos casos. O fato de que, após o valor n = 5000 , o número de casos de solução do problema de configuração sem o uso do procedimento BT está diminuindo gradualmente, está associado ao modelo selecionado para selecionar os valores de limite de baseLevel2 e baseLevel3 . Você pode alterar esses parâmetros e obter um aumento no número de soluções sem usar o procedimento BT. No entanto, isso levará a um aumento no tempo de cálculo, uma vez que a participação do quinto bloco na operação do algoritmo aumentará.

O histograma da distribuição da separação do tempo . Na Figura 10, para um valor de n = 1000é apresentado um histograma da distribuição do tempo de separação para um milhão de soluções. A visão não muito comum do histograma de distribuição (que provavelmente se assemelha à silhueta noturna de edifícios altos) não está associada a um erro na seleção da duração ou do número de intervalos. Essa é uma propriedade natural desse algoritmo. Para entender,

Fig. 10. Um histograma do tempo de compilação de composições de tamanhos arbitrários. ( n = 1000 ; tamanho da amostra = 1.000.000 )

Por que o histograma tem esse formato, considere a distribuição do tempo de separação para composições que tenham o mesmo tamanho. Para isso, como exemplo, a partir da amostra inicial, selecionaremos todas as composições cujo tamanho é 800. Havia 998 dessas composições em uma amostra de um milhão. A Figura 11 mostra um histograma da distribuição do tempo de contagem para esta amostra. Pode-se ver pela figura que a distribuição consiste em seis histogramas separados, com tamanhos decrescentes.

Fig. 11. Um histograma do tempo de compilação de composições do mesmo tamanho (k = 800). ( n = 1000 ; tamanho da amostra = 998 )

A razão pela qual o tempo de compilação de 998 composições, em cada uma das quais 800 rainhas são distribuídas aleatoriamente, é "agrupado" em 6 grupos, porque o procedimento Back Tracking é usado. O primeiro histograma da figura, com o tamanho máximo da amostra, são aquelas que selecionam soluções em que o procedimento BT nunca foi usado. Este é um grupo das soluções mais rápidas. O segundo histograma, que é significativamente menor em tamanho que o primeiro, são aquelas soluções em que o procedimento BT foi usado apenas uma vez. Portanto, o tempo de decisão nesse grupo é um pouco mais longo que no primeiro. Por conseguinte, no terceiro grupo, o procedimento BT foi utilizado duas vezes, no quarto - três vezes, etc., ou seja, As decisões nas quais o procedimento BT foi utilizado repetidamente foram realizadas por um período maior. Tais soluções formam a cauda direita longa da distribuição desejada.

Soluções de falso negativo . Se dividirmos todas as composições possíveis para um valor arbitrário de npositivo e negativo, entre as composições positivas, existem aquelas que esse algoritmo pode classificar como negativo. Isso se deve ao fato de que, dentro dos limites estabelecidos pelos parâmetros de pesquisa, o algoritmo não consegue encontrar o caminho certo para concluir essas composições. Como mostram os resultados experimentais (Tabela 2), o número de casos não excede 0,0001 do tamanho da amostra e o valor desse erro diminui com o aumento de n . Além disso, para todos os valores de n> 800, não houve um único caso de solução de falso negativo . Mesmo aumentar o tamanho da amostra para um milhão para n = 1000 não resultou em falso negativodecisões. O resultado nos permite formular a seguinte regra para resolver o problema: “Qualquer composição aleatória de k rainhas que é distribuída consistentemente em um tabuleiro de xadrez arbitrário de tamanho nxn pode ser concluída até que uma solução completa seja feita, ou será decidido que essa composição é negativa e não pode para ser completado. A probabilidade de tomar tal decisão não excede 0,0001 . À medida que o tamanho de um tabuleiro de xadrez aumenta, a probabilidade de tomar decisões erradas diminui. A complexidade do tempo do algoritmo é linear. ”

8. Conclusões

1. É apresentado um algoritmo que permite, em tempo linear, resolver o problema do conjunto completo até uma solução completa de uma composição aleatória de k rainhas, distribuída consistentemente em um tabuleiro de xadrez de tamanho arbitrário nxn . Além disso, para qualquer composição de k rainhas ( 1≤ k <n ), é fornecida uma solução, se houver, ou é tomada uma decisão de que essa composição não pode ser concluída. A probabilidade de um erro ao tomar essa decisão não excede 0,0001 e esse valor diminui com o aumento do tamanho de um tabuleiro de xadrez.

2. A operação deste algoritmo é baseada no uso de duas regras importantes:

a) Na fase final de solução do problema, dentre todas as linhas livres restantes, é selecionada uma para a qual o número de posições livres é mínimo ( regra de risco mínimo ). Isso minimiza os riscos associados à possibilidade de excluir as últimas posições vagas em algumas das linhas restantes.

b) De todas as posições vagas na linha em questão, essa posição é selecionada que causa dano mínimo às posições livres nas linhas livres restantes ( regra de dano mínimo ). Por " dano mínimo " entende-se a seleção dessa posição em uma linha que exclui a menor quantidade de posições livres em todas as linhas livres restantes.

3. Foi estabelecido que, como resultado da operação desse algoritmo, o tempo médio necessário para a rainha ser colocada em uma linha diminui com um aumento no valor de n. O tempo médio necessário para colocar a rainha em uma linha no caso em que n é 10 ⁸ é 21 vezes menor que o tempo correspondente para o caso n = 50.

4. Verificou-se que, no intervalo de valores n = (7, ..., 100000), o número de soluções nas quais o procedimento de rastreamento de retorno nunca foi usado excede 35%. Além disso, no intervalo de valores n = (320, ..., 22500) , o número de casos excede 50%, o que indica a alta eficiência desse algoritmo.

5. Um modelo para organizar o procedimento de Back Tracking é proposto, com base na divisão da sequência de etapas da decisão em níveis básicos. Um nível significa uma determinada etapa de decisão com um determinado número de rainhas corretamente colocadas . As fórmulas de regressão são fornecidas para o cálculo dos valores do segundo e terceiro níveis básicos, dependendo de n .

6. Os resultados de uma análise comparativa de dois métodos de seleção aleatória, denominados randSet e randSet e rand & rand , são apresentados . O algoritmo randSet e randSet foi considerado rápido, mas rude. Portanto, seu uso é limitado ao atingir o segundo nível básico. Depois disso, o algoritmo rand & rand é usado, o que não é tão rápido, mas coloca rainhas de forma mais eficiente no tabuleiro de xadrez.

7. Um algoritmo eficaz para verificar a correção da solução do problema n-Queens é fornecido. Este programa também foi projetado para verificar a correção de uma composição aleatória de tamanho arbitrário. O programa funciona rápido o suficiente. Por exemplo, o tempo necessário para validar uma solução que consiste em 5 milhões de posições é de 0,85 segundos.

9. Comentários

1. Conforme indicado no início do artigo, foram realizados estudos na faixa de n valores, de 7 a 100 milhões. No entanto, o programa foi testado em uma faixa mais ampla de n valores, até um bilhão. É verdade que, no último caso, o programa teve que ser ligeiramente adaptado, dado o grande tamanho das matrizes. Portanto, se o tamanho da RAM permitir, é possível realizar cálculos para grandes valores de n.

2. Os valores dos indicadores da linha de base, bem como os valores limites do número de repetições em vários níveis, foram otimizados para resolver o problema em toda a faixa de pesquisa. Eles podem ser alterados dentro de um intervalo menor e reduzir o tempo de contagem. É importante não aumentar a participação das soluções de falso negativo .

3. Neste artigo, usei o tempo de pressionamento da tecla Enter como uma medida de tempo para avaliar a rapidez com que o algoritmo funciona. Se o resultado aparecer imediatamente após pressionar a tecla, no nível da percepção do usuário, parece que o programa funciona "muito" rapidamente. Não importa a rapidez com que o algoritmo funcione, o resultado não aparecerá na tela até que a chave seja concluída. Portanto, pareceu-me que essa medida condicional do tempo pode servir como um nível limite para não comparar estritamente a velocidade de vários algoritmos.

4. Filosófico ... Durante o estudo, foi considerado um grande número de publicações relacionadas à solução de problemas não determinísticos. Na maioria dos casos, essas eram tarefas nas quais era necessário fazer uma escolha em um grande espaço de estados, sob as condições de determinadas restrições. Comparando-os, foi interessante saber até que ponto podemos avançar na solução de tais problemas usando a abordagem matemática padrão. Tive a impressão de que é impossível resolver esses problemas apenas com base em definições, afirmações de lemas e provas de teoremas. Parece-me que, para resolver esses problemas, é necessário usar os métodos da matemática algorítmica usando simulação por computador. Para demonstrar a validade dessa conclusão, como exemplo simples, preparei para o tabuleiro de xadrez, cujo tamanho é 10 ⁹ x 10 ^9, duas composições do mesmo tamanho, consistindo em 999.999.482 rainhas. Eles são preparados conforme descrito no início do artigo e apresentados em dois arquivos no formato .mat. Eles podem ser baixados neste link (dois arquivos de teste) . Os arquivos são bastante "pesados", o tamanho de cada um deles é de cerca de 3,97 Gb. Em 999 997 976 linhas (em 99,99998% dos casos), as posições das rainhas em ambas as composições coincidem, e somente em 1506 linhas arbitrárias as posições das rainhas diferem.

Para concluir os dados de composição para uma solução completa, é necessário colocar corretamente as rainhas nas 518 linhas livres restantes. O número de maneiras possíveis de organizar 518 rainhas nas linhas livres restantes (levando em consideração apenas o número de maneiras de selecionar uma posição livre na linha selecionada) é de aproximadamente 10 ¹⁴⁶⁶ . A diferença entre essas duas composições consiste apenas no fato de que uma delas é positiva e pode ser completada até uma solução completa, e a outra composição é negativa - ela não pode ser completada até uma solução completa. Pergunta: “É possível, com base em uma abordagem matemática rigorosa (isto é, sem realizar operações computacionais algorítmicas), determinar qual dessas duas composições é positiva?” Se isso é impossível de resolver, podemos assumir que a proposição feita é comprovada por contradição.

Quero observar que, independentemente da abordagem estritamente matemática deste problema, é necessário determinar o status de 518 * 10 ⁹ células nas demais linhas livres. Para fazer isso, é necessário considerar cada posição de rainhas estabelecidas anteriormente, e existem quase um bilhão delas, a fim de estabelecer as restrições que cada rainha estabelecida impõe a posições livres nas 518 linhas restantes. Não encontrei um "ponto de apoio" que me permitisse fazer esse trabalho apenas com base em uma abordagem estritamente matemática, sem cálculos algorítmicos.

Dei aqui um exemplo mínimo que consiste em apenas duas composições. Se necessário, o número de tais composições pode ser aumentado.

Deve-se notar que, com base no algoritmo linear proposto, ligeiramente adaptado para trabalhar com grandes composições, cujas tarefas podem ser concluídas antes que uma solução completa seja executada na área de trabalho-13 , em cerca de 4,5 minutos (excluindo o tempo de carregamento dados de entrada).

10. Adição

A ação de professores que recomendam tarefas capazes para os alunos desenvolverem e pesquisarem é digna de respeito. Isso requer um esforço considerável, mas, superando dificuldades, o pesquisador observa outras tarefas complexas de maneira diferente. Eu pensei que seria útil expandir as opções para definir o problema do n-Queens para tais propósitos. Se você observar a mesma tarefa de perspectivas diferentes, poderá ver coisas diferentes. Abaixo estão alguns deles.

1. Considere o problema de organizar n rainhas em um tabuleiro retangular de xadrez de tamanho nxm . Denote k = m - n . Seja obtida alguma solução e em cada uma das n linhas uma rainha deve ser localizada. Excluímos as posições em que as rainhas estão localizadas de uma análise mais aprofundada. Agora em cada linha existe a posição livre m-1 . Nas demais posições livres, encontramos novamente uma solução. Como antes, excluímos de uma análise mais aprofundada as posições em que as rainhas da segunda solução estão localizadas. Agora em cada linha existem m-2 posições livres. Obviamente, a primeira e a segunda soluções não se cruzam em suas posições em nenhuma linha - elas são ortogonais. É necessário determinar o número máximo de soluções mutuamente ortogonais para vários valores de k . Se n soluções mutuamente ortogonais forem encontradas para o valor k = 0 , o Royal Latin Square será construído.

Observação . Grigoryan E. (2018) mostrou que, para qualquer solução do Problema n-Queens , existe uma solução complementar que não se cruza com ela. Isso significa que, para um valor arbitrário de n , o conjunto de todas as soluções do problema n-Queens é dividido em dois subconjuntos de tamanho igual . Qualquer solução do segundo subconjunto é uma solução complementar à solução correspondente do primeiro subconjunto. A regra é bastante simples, se Q1 (i) é uma solução do primeiro conjunto, a solução complementar correspondente Q2 (i) do segundo subconjunto é determinada pela fórmula Q2 (i) = n + 1 - Q1 (i), onde i = (1, ... , n) É essa regra que explica o fato de que o número de todas as soluções do problema n-Queens , para um valor arbitrário de n , é sempre um número par. (Esta regra nos permite reduzir pela metade o tempo para calcular todas as soluções completas para um tamanho arbitrário n do tabuleiro de xadrez. Se denotarmos por 2 * k o número total de todas as soluções, o valor k será igual ao índice na lista seqüencial de todas as soluções quando Q (k) + Q ( k + 1) = n + 1 ).

2. Na formulação inicial do problema do problema n-Qeens , depois que a rainha é colocada na posição (i, j) , são executadas as seguintes ações:

a) excluir todas as células da linha ie coluna j

b) todas as células localizadas na linha das diagonais esquerda e direita que passam pela célula (i, j) são excluídas.

Mudamos a condição b) na declaração do problema. Em vez de eliminar células, usaremos a troca de células. Se a célula localizada na linha das diagonais esquerda ou direita estiver livre, nós a fecharemos; se a célula estiver fechada, então a abriremos. Isso facilita a localização de uma solução. No entanto, em vez da matriz quadrada nxn , consideramos uma matriz retangular de tamanho nx (n - k) . É necessário, para um dado valor de n , encontrar o valor máximo de k no qual pelo menos três soluções ortogonais possam ser obtidas. Como o valor de k mudará com o aumento do valor de n ?

3. Altere algumas condições na formulação inicial do problema do problema n-Queens . Quando a rainha é colocada na posição (i, j) em um tabuleiro de xadrez de tamanho nxn :

a) excluir todas as células da linha i ,

b) se o índice j for um número par, então:

b1) excluir células em linhas pares da coluna j,

b2) excluímos células em linhas pares que se cruzam com as diagonais esquerda e direita passando pela célula (i, j) ,

c) Se o índice j for um número ímpar, os pontos b1) e b2) serão satisfeitos para células localizadas em linhas ímpares.

3.1 Sabe-se (Sloane-2016) que a lista de valores de todas as soluções do problema nQueens , para n = (8, 9, 10, 11, 12, 13, 14, 15, 16) , respectivamente, é (92, 352, 724, 2680, 14200, 73712, 365596, 2279184, 14772512) . Como o número de todas as soluções mudará se, na declaração do problema, a condição padrão para exceções diagonais for alterada para o parágrafo b) ou o parágrafo c)?

3.2 É sabido por Grigoryan (2018) que, se determinarmos a frequência de participação de diferentes células da matriz da solução na formação de uma lista de todas as soluções, podemos descobrir que há relações harmoniosas entre todas as células na forma de simetrias verticais e horizontais das frequências correspondentes. Isso significa que, se assumirmos que k <n / 2 , a frequência das células da k-ésima linha será idêntica às frequências das células da linha n-k + 1 . Da mesma forma, a frequência das células da k-ésima coluna será idêntica às frequências das células da coluna n-k + 1 . Pergunta: “Como essas relações harmoniosas mudarão no contexto da tarefa?”

4. Todas as células de um tabuleiro de xadrez são divididas em duas classes por sua cor. Acredita-se que uma cor seja branca e a outra preta. Considere dois tabuleiros de xadrez e coloque um deles no outro para que as bordas coincidam completamente. Como resultado, obtemos um "sanduíche" de dois tabuleiros de xadrez, nos quais o arranjo das células brancas e pretas coincide. A tarefa é encontrar soluções simultaneamente em duas placas, observando as seguintes condições:

a) Se em uma das placas a rainha estiver localizada em uma célula preta com índices (i, j) , então:

- em ambas as placas, todas as células pretas encontradas na linha ie coluna j são excluídas

- em ambas as placas, todas as células pretas localizadas ao longo das diagonais esquerda e direita que passam pela célula (i, j) são excluídas.

b) Se em uma das placas a rainha estiver localizada em uma célula branca com índices (i, j) , todas as ações do parágrafo a) serão realizadas apenas para células brancas.

5. Imagine que em uma matriz de solução do tamanho nxn , as linhas podem deslizar uma em relação à outra à direita ou à esquerda, com uma etapa de k células. Além disso, se a linha anterior foi deslocada, por exemplo, para a esquerda, a próxima linha deve ser deslocada para a direita, ou seja, cada linha seguinte é deslocada na direção oposta à linha anterior. Como resultado dessa construção, obtemos uma matriz retangular de tamanho nx (n + k) , onde em cada linha k células do início da linha ou do final serão excluídas da consideração. A tarefa é encontrar o valor máximo de k para um valor arbitrário de n para o qual existe pelo menos uma solução n-Problema do Queens .
Considere uma variante do problema em que o deslocamento de uma linha em relação a outra é um número aleatório que varia de k1 a k2 .

6. A formulação unidimensional do problema nQueens . Deixe n segmentos de comprimento arbitrário, numerados de 1 a n , dispostos no semi-eixo. Divida cada segmento em n células de tamanho arbitrário e, em cada segmento, numere células de 1 a n . Chamamos essas células de abertas. É necessário fechar uma célula em cada segmento, levando em consideração as seguintes restrições:

a) Podemos escolher uma célula aberta com o número j do i- ésimo segmento, se:

D1 (r) = 0;

D2 (t) = 0;

onde r = n + j - i, t = j + i, D1 e D2 são matrizes de controle unidimensional que consistem em 2n células que foram zeradas anteriormente.

b) Após essa seleção, o segmento ie células com o número j serão fechadas em todos os demais segmentos livres. Também é necessário fechar as células correspondentes nas matrizes de controle:

D1 (r) = 1;

D2 (t) = 1;

Nessa configuração, a tarefa é completamente idêntica à original. De interesse é a formulação desse problema com outras condições de restrição. Por exemplo, se em vez de fórmulas:
r = n + j - i, t = j + i ,,
serão consideradas outras relações que conectam funcionalmente os índices r e t aos índices (i, j) da matriz de decisão.

7. A redação da tarefa com base em uma urna com bolas (idêntica à redação anterior). Que haja n urnas numeradas de 1 a n , e em cada urna há n bolas, também numeradas de 1 a n . É necessário selecionar uma bola de cada urna, levando em consideração as seguintes restrições:

a) Podemos escolher uma bola com o número j da iª urna se:

D1 (r) = 0 ,

D2 (t) = 0 ,

onde r = n + j - i, t = j + i, D1 e D2 são matrizes de controle unidimensional que consistem em 2n células que foram zeradas anteriormente.

b) Após essa escolha, as urnas de votação ie as bolas com número j serão fechadas em todas as urnas restantes restantes. Também é necessário fechar as células correspondentes nas matrizes de controle:

D1 (r) = 1

D2 (t) = 1 .

Nessa configuração, a tarefa é completamente idêntica à original. Como no caso anterior, a declaração deste problema com outras condições que conectam funcionalmente os índices r e t com os índices (i, j) da matriz de decisão é de interesse.

8. o jogo Considere um tabuleiro de xadrez de tamanho nxn . Vamos devolver a cor às rainhas, deixar algumas rainhas de cor branca, outras pretas. Também devolvemos a cor branca e preta alternada às células do tabuleiro de xadrez, com base no fato de que a célula com o índice (1, n) deve ser branca. Todas as células no início do jogo são consideradas livres. Rainhas brancas fazem o primeiro movimento. O jogador coloca a rainha em uma célula livre arbitrária com índices (i, j) . Que seja uma célula branca. Como resultado dessa escolha, feche:

a) todas as células brancas da linha i ,

b) todas as células brancas da coluna j ,

c) todas as células brancas que se encontram nas diagonais esquerda e direita que passam através da célula (i, j) .

Se a célula (i, j) for preta, todos os itens (a, b, c) serão satisfeitos e, portanto, todas as células em preto serão fechadas. Em seguida, as pretas executam o movimento, colocando a rainha em qualquer uma das células livres restantes. Depois disso, de maneira semelhante, as células se fecham, como descrito acima. O tempo para pensar sobre a próxima jogada é fixo e é selecionado por acordo das partes. Se durante o tempo especificado, um dos jogadores não concluir sua jogada, o jogo será transferido para o outro. O jogo termina se ambos os jogadores, um após o outro, falharem em completar o turno no tempo especificado. Quem pode colocar mais rainhas no tabuleiro vence.

9. Sobre a estabilidade da seleção aleatória. Considere o modelo randSet e randSet .Como resultado da comparação de n pares aleatórios de índices de linha e coluna, no primeiro estágio do ciclo, é possível estabelecer rainhas em média em k * n linhas. O valor de k pode ser considerado um valor constante igual a 0,6. Seu valor varia de 0,605701 em n = 10 e 0,599777 em n = 10 ⁶ e, com o aumento de n , a variação desse valor diminui. Qual é o motivo dessa "constância"? Por que, com uma seleção aleatória do índice de linha e o índice de posição da rainha nesta linha, com base em duas listas de números obtidos com base em uma permutação aleatória de números de 1 a n, é possível colocar consistentemente as rainhas (em média) em 60% das linhas?

10. Deixe o tamanho do tabuleiro de xadrez igualnxn . Com base nos procedimentos randSet e randSet , colocamos as rainhas no tabuleiro de xadrez até que o ramo de pesquisa atinja o beco sem saída. Indique o comprimento da composição assim obtida por k . Se, para um determinado valor de n, repetir esse procedimento várias vezes e construir um histograma da distribuição dos valores de k , verifica-se que a alteração na frequência de ocorrência de eventos no valor do modo de distribuição difere da alteração na frequência de ocorrência de eventos após esse valor. Se, com base no valor modal, o histograma for dividido em duas partes, a parte esquerda não coincidirá com a parte direita. Esse padrão é característico para qualquer valor de n. Por que, após a transição do comprimento da composição pelo valor modal, a frequência de ocorrência de eventos assume uma forma diferente? Por um evento, queremos dizer receber uma composição de um determinado tamanho, antes de atingir um estado de impasse.

Literatura

1. Nauck, F. (1850). Briefwechsel mit allen fur alle . Illustrierte Zeitung, 15, 182.

2. Gent, IP, Jefferson, C. & Nightingale, P. (2017). Complexidade da conclusão de n-Queens ,
Journal of Artificial Intelligence Research., 59, 815-848.

3. Sosic, R., & Gu, J. (1990). Um algoritmo de tempo polinomial para o problema n-rainhas . Boletim SIGART, 1 (3), 7–11.

4. Richards, M. (1997). Algoritmos de retrocesso no MCPL usando padrões de bits e recursão .
Tech. rep., Laboratório de Informática, Universidade de Cambridge.

5. Métodos de Randomização no Design de Algoritmos, Anais de um Workshop DIMACS, Princeton, Nova Jersey, EUA, 12-14 de dezembro de 1997. Série DIMACS em Matemática Discreta e Ciência da Computação Teórica 43, DIMACS / AMS 1999, ISBN 978-0-8218-0916-7

6. Grigoryan E. (2018). Investigação das regularidades na formação de soluções n-Queens Problem . Modelagem de Inteligência Artificial, 5 (1), 3-21

7. Sloane N.-JA (2016). A enciclopédia on-line de seqüências inteiras.

Problema de conclusão do n-Queens - algoritmo de solução linear