Aprendizado por reforço profundo: como ensinar aranhas a andar

Hoje vou contar como apliquei algoritmos de aprendizado profundo de reforço para controlar um robô. Em resumo, vou lhe mostrar como criar uma "caixa preta com redes neurais", que aceita a arquitetura do robô na entrada e gera um algoritmo que pode controlá-lo na saída.

O núcleo da solução é o algoritmo Advantage Actor Critic (A2C) com pontuações Advantage por meio da Generalized Advantage Estimation (GAE).

Sob o corte, a matemática, uma implementação do TensorFlow e muitas demonstrações do tipo de algoritmo de caminhada.

Conteúdo:

- Conclusão

Desafio

Neste artigo, ensinaremos o robô a andar na simulação MuJoCo. Iremos pular a descrição da etapa criando um modelo do robô e a interface Python para o ambiente, porque não há nada interessante lá. Para entender, basta olhar para as demos no próprio MuJoCo e as fontes dos ambientes do MuJoCo no Gym OpenAI .

Na entrada, o agente terá muitos números de MuJoCo: posições relativas, ângulos de rotação, velocidade, aceleração de partes do corpo do robô, etc. No total, a ordem de ~ 800 recursos. Utilizamos a abordagem Deep Learning e não entenderemos o que eles realmente significam. O principal é que, nesse conjunto de números, haverá informações suficientes para que o agente possa entender o que está acontecendo com ele.

Na saída, esperaremos 18 números - o número de graus de liberdade do robô, o que significa os ângulos de rotação das dobradiças nas quais os membros estão fixos.

Por fim, o objetivo do agente é maximizar a recompensa total para o episódio. Terminaremos o episódio se o robô travar ou se 3000 etapas tiverem passado (15 segundos). Cada etapa recompensará o agente de acordo com a seguinte fórmula:

I.e. o objetivo do agente aumentará sua coordenada $$$x$ e não caia até o final do episódio.

Então, a tarefa é: encontrar uma função $$$\ pi: \ R ^ {800} \ to \ R ^ {18}$ pelo qual a recompensa pelo episódio será a maior . Isso não parece muito certo? :) Vamos ver como o Deep Reinforcement Learning lida com essa tarefa.

Por que aprender reforço?

As abordagens modernas para resolver o problema do movimento de robôs ambulantes consistem em práticas clássicas de robótica, nas seções controle otimizado e otimização de trajetória : LQR, QP, otimização convexa. Leia mais: Postagem da equipe do Boston Dynamics no Atlas .

Essas técnicas são uma espécie de "codificação", porque exigem a introdução de muitos detalhes da tarefa diretamente no algoritmo de controle. Não há sistemas de aprendizagem neles - a otimização ocorre "no local".

Por outro lado, o Aprendizado por Reforço (daqui em diante RL) não requer hipóteses no algoritmo, tornando a solução do problema mais geral e escalável.

Declaração de Aprendizado por Reforço

Fonte

No problema de RL, consideramos a interação do agente e o ambiente como uma sequência de pares (estado, recompensa) e as transições entre eles - ação .

Defina a terminologia:

• $$$\ pi (a_t | s_t)$ - política , estratégia de comportamento do agente, probabilidade condicional,
• $$$a_t \ sim \ pi (\ cdot | s_t)$ - ação é considerada uma variável aleatória da distribuição $$$\ pi$ ,
  Poderíamos considerar a política como uma função $$$\ pi: States \ to Ações$ , mas queremos tornar as ações do agente estocásticas, o que facilita a exploração . I.e. com alguma probabilidade, não realizamos as ações que o agente escolhe.
• $$$\ tau$ - trajetória traçada pelo agente, sequência $$$(s_1, s_2, ..., s_n)$ .

A tarefa do agente é maximizar o retorno esperado :

Agora podemos formular o problema da RL, encontre:

onde $$$\ pi ^ *$ É a política ideal.

Leia mais no material da OpenAI: OpenAI Spinning Up .

Gradiente de política

Vale ressaltar que uma declaração rigorosa do problema de RL como um problema de otimização nos dá a oportunidade de usar os métodos de otimização já conhecidos, por exemplo, descida em gradiente . Imagine como seria legal se pudéssemos pegar o gradiente de retorno esperado pelos parâmetros do modelo : $$$\ nabla_ \ theta J (\ pi_ \ theta)$ . Nesse caso, a regra para atualizar as escalas seria simples:

Essa é precisamente a idéia de todos os métodos de gradiente de políticas . A conclusão estrita desse gradiente é um tanto incondicional. Não vamos escrever aqui, mas deixar um link para o maravilhoso material da OpenAI . O gradiente fica assim:

Assim, a perda do nosso modelo será assim:

Lembre-se que $$$R (\ tau) = \ sum_ {t = 0} ^ T r_t$ e $$$\ pi_ \ theta (a_t | s_t)$ - esta é a saída do nosso modelo no momento em que ela estava $$$s_t$ . O menos apareceu devido ao fato de que queremos maximizar $$$J$ . Durante o treinamento, consideraremos o gradiente nos lotes e os adicionaremos para reduzir a variação (ruído de dados devido ao ambiente estocástico).

Este é um algoritmo de trabalho chamado REFORÇAR . E ele sabe como encontrar soluções para alguns ambientes simples. Por exemplo, "CartPole-v1" .

Considere o código do agente:

class ActorNetworkDiscrete: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=20, activation=tf.nn.relu) output_linear = tf.layers.dense(l1, units=action_space) output = tf.nn.softmax(output_linear) self.action_op = tf.squeeze(tf.multinomial(logits=output_linear,num_samples=1), axis=1) # Training output_log = tf.nn.log_softmax(output_linear) self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None], dtype=tf.int32) action_one_hot = tf.one_hot(self.action_ph, action_space) responsible_output_log = tf.reduce_sum(output_log * action_one_hot, axis=1) self.loss = -tf.reduce_mean(responsible_output_log * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss) actor = ActorNetworkDiscrete() 

Temos um pequeno perceptron dessa arquitetura: (o espaço de observação, 10, o espaço de ação) [para CartPole, este é (4, 10, 2)]. tf.multinomial permite escolher uma ação ponderada aleatoriamente. Para obter uma ação, você precisa ligar para:

 action = sess.run(actor.action_op, feed_dict={actor.state_ph: observation}) 

E assim vamos treiná-lo:

 batch_generator = generate_batch(environments, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, total reward] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]}) 

O gerador de lotes executa o agente no ambiente e acumula dados para treinamento. Os elementos do lote são tuplas deste tipo: $$$(s_t, a_t, R (\ tau))$ .

Escrever um bom gerador é uma tarefa separada, onde a principal dificuldade é o alto custo relativo da chamada sess.run () em comparação com uma única etapa de simulação (mesmo MuJoCo). Para acelerar o trabalho, você pode explorar o fato de que as redes neurais são executadas em lotes e usam muitos ambientes paralelos. Mesmo iniciá-los sequencialmente em um thread dará uma aceleração significativa em comparação com um único ambiente.

 # Vectorized environments with gym-like interface from baselines.common.vec_env.subproc_vec_env import SubprocVecEnv from baselines.common.vec_env.dummy_vec_env import DummyVecEnv def make_env(env_id, seed): def _f(): env = gym.make(env_name) env.reset() # Desync environments for i in range(int(200 * seed // environments_count)): env.step(env.action_space.sample()) return env return _f envs = [make_env(env_name, seed) for seed in range(environments_count)] # Can be switched to SubprocVecEnv to parallelize on cores # (for computationally heavy envs) envs = DummyVecEnv(envs) # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py def discount_cumsum(x, coef): """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def generate_batch(envs, batch_size, replay_buffer_size): envs_number = envs.num_envs observations = [[0 for i in range(observation_space)] for i in range(envs_number)] # [state, action, discounted reward-to-go] replay_buffer = np.empty((0,3), np.float32) # [state, action, reward] rollout lists for every environment instance rollouts = [np.empty((0, 3)) for i in range(envs_number)] while True: history = {'reward': [], 'max_action': []} replay_buffer = replay_buffer[batch_size:] # Main sampling cycle while len(replay_buffer) < replay_buffer_size: # Here policy acts in environments. Note that it chooses actions for all # environments in one batch, therefore expensive sess.run is called once. actions = sess.run(actor.action_op, feed_dict={actor.state_ph: observations}) observations_old = observations observations, rewards, dones, _ = envs.step(actions) history['max_action'].append(np.abs(actions).max()) time_point = np.array(list(zip(observations_old, actions, rewards))) for i in range(envs_number): # Regular python-like append rollouts[i] = np.append(rollouts[i], [time_point[i]], axis=0) # Process done==True environments if dones.all(): print('WARNING: envs are in sync!! This makes sampling inefficient!') done_indexes = np.arange(envs_number)[dones] for i in done_indexes: rewards_trajectory = rollouts[i][:, 2].copy() history['reward'].append(rewards_trajectory.sum()) rollouts[i][:, 2] = discount_cumsum(rewards_trajectory, coef=discount_factor) replay_buffer = np.append(replay_buffer, rollouts[i], axis=0) rollouts[i] = np.empty((0, 3)) # Shuffle before yield to become closer to iid np.random.shuffle(replay_buffer) # Truncate replay_buffer to get the most relevant feedback from environment replay_buffer = replay_buffer[:replay_buffer_size] yield replay_buffer[:batch_size], history # Make a test yield a = generate_batch(envs, 8, 64) # Makes them of equal lenght for i in range(10): next(a) next(a)[0] 

O agente resultante pode jogar em ambientes com um espaço finito de ações . Este formato não é adequado para a nossa tarefa. O agente que controla o robô deve emitir um vetor de $$$\ R ^ n$ onde $$$n$ - o número de graus de liberdade. ( ou você pode dividir o espaço de ação em intervalos e obter uma tarefa com uma saída discreta )

Políticas gaussianas diagonais

A essência da abordagem de políticas gaussianas diagonais é que o modelo produza parâmetros da distribuição normal n-dimensional, a saber $$$\ mu_ \ theta$ - tapete. esperando e $$$\ sigma_ \ theta$ desvio padrão. Assim que o agente precisar executar uma ação, solicitaremos esses parâmetros no modelo e tiraremos uma variável aleatória dessa distribuição. Então fizemos o agente sair $$$\ R ^ n$ e tornou estocástico. O mais importante é que, tendo fixado a classe de distribuição na saída, podemos calcular $$$\ log (\ pi_ \ theta (a_t | s_t))$ e, portanto, gradiente político.

Nota: pode ser corrigido $$$\ sigma_ \ theta$ como um hiperparâmetro, reduzindo assim a dimensão da saída. A prática mostra que isso não causa muito dano, mas, pelo contrário, estabiliza o aprendizado.

Leia mais sobre política estocástica .

Código do agente:

 epsilon = 1e-8 def gaussian_loglikelihood(x, mu, log_std): pre_sum = -0.5 * (((x - mu) / (tf.exp(log_std) + epsilon))**2 + 2 * log_std + np.log(2 * np.pi)) return tf.reduce_sum(pre_sum, axis=1) class ActorNetworkContinuous: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) mu = tf.layers.dense(l3, units=action_space) log_std = tf.get_variable(name='log_std', initializer=-0.5 * np.ones(action_space, std = tf.exp(log_std) self.action_op = mu + tf.random.normal(shape=tf.shape(mu)) * std # Training self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None, action_space], dtype=tf.float32) action_logprob = gaussian_loglikelihood(self.action_ph, mu, log_std) self.loss = -tf.reduce_mean(action_logprob * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss) 

A parte do treinamento não é diferente.

Agora finalmente podemos ver como o REFINFORCE lidará com a nossa tarefa. A seguir, o objetivo do agente é mover para a direita.

Lenta mas seguramente rastejando em direção a seu objetivo.

Recompensa para viagem

Observe que existem membros extras em nosso gradiente. Ou seja, para cada etapa $$$t$ ao pesar o gradiente do logaritmo, usamos a recompensa total para toda a trajetória . Assim, avaliando as ações do agente por suas realizações do passado. Parece errado, não é? Portanto, este

vai se tornar isso

Encontre 10 diferenças :)

Embora a presença desses membros não estrague nada matematicamente, isso faz muito barulho para nós. Agora, durante o treinamento, o agente prestará atenção apenas às recompensas que recebeu após uma ação específica .

Devido a essa melhoria, a recompensa média aumentou. Um dos agentes recebidos aprendeu a usar os membros anteriores para alcançar seu objetivo:

Reduza a variação adicionando críticas

A essência de outras melhorias é a redução do ruído (variação) decorrente das transições estocásticas entre os estados do meio.

Isso nos ajudará a adicionar um modelo que preveja a quantidade média de recompensas recebidas pelo agente, a partir do estado $$$s$ até o final da trajetória, ou seja, Função de valor.

A função Valor mostra o retorno esperado se nossa política iniciar o jogo a partir de um estado específico. O mesmo com a função Q, basta corrigir a primeira ação.

Adicionar crítica

É assim que o gradiente fica ao usar o Reward-to-Go:

Agora, o coeficiente para o gradiente do logaritmo nada mais é do que uma amostra da função Valor.

Pesamos o gradiente de logaritmo com uma amostra de uma trajetória específica, o que não é bom. Podemos aproximar a função Valor com algum modelo, por exemplo, uma rede neural, e solicitar o valor necessário, reduzindo assim a variação. Chamaremos esse modelo de crítico (Critic) e o estudaremos em paralelo com a política. Assim, a fórmula do gradiente pode ser escrita como:

Reduzimos a variação, mas, ao mesmo tempo, introduzimos o viés em nosso algoritmo, já que as redes neurais podem cometer erros de aproximação. Mas o compromisso nessa situação é bom. Tais situações no aprendizado de máquina são chamadas de troca de viés e variância .

O crítico ensinará a regressão da função Valor em amostras de recompensa coletadas no ambiente. Como uma função de erro, tomamos o MSE. I.e. perda é assim:

Código crítico:

 class CriticNetwork: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) output = tf.layers.dense(l3, units=1) self.value_op = tf.squeeze(output, axis=-1) # Training self.value_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.loss = tf.losses.mean_squared_error(self.value_ph, self.value_op) optimizer = tf.train.AdamOptimizer(learning_rate=critic_learning_rate) self.update_op = optimizer.minimize(self.loss) 

O ciclo de treinamento agora fica assim:

 batch_generator = generate_batch(envs, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, value, reward-to-go] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]}) # Train critic for j in range(10): _, critic_loss = sess.run([critic.update_op, critic.loss], feed_dict={critic.state_ph: batch[:, 0], critic.value_ph: batch[:, 3]}) 

Agora, o lote contém outro valor, valor calculado pelo crítico no gerador.
I.e. o tipo de lote é este: $$$(s_t, a_t, V ^ \ pi_ \ psi (s_t), \ sum_ {t '= t} ^ T r_ {t'})$ .

No ciclo, nada nos limita a treinar o crítico para a convergência , por isso tomamos várias etapas de descida gradiente, melhorando a aproximação da função Value e reduzindo o viés. No entanto, essa abordagem requer um tamanho de lote grande para evitar a reciclagem. Uma afirmação semelhante sobre política de aprendizagem não é verdadeira. Ele deve receber feedback instantâneo do ambiente de aprendizado; caso contrário, podemos nos encontrar em uma situação em que multamos a política por ações que ela ainda não teria tomado. Algoritmos com essa propriedade são chamados na política .

Linhas de base em gradientes de políticas

Pode-se demonstrar que no gradiente é permitido colocar uma ampla classe de outras funções úteis de $$$t$ . Tais funções são chamadas de linhas de base . ( Conclusão deste fato ) As seguintes funções têm bom desempenho como linhas de base:

Fonte: artigo do GAE .

Linhas de base diferentes fornecem resultados diferentes, dependendo da tarefa. Como regra, o maior lucro é dado pela função Advantage e suas aproximações.

Há até um pouco de intuição por trás disso. Quando usamos o Advantage, multamos o agente na proporção de quanto melhor ou pior que a média o agente considera a ação que ele executou. E quanto melhor o agente joga no ambiente, mais altos se tornam seus padrões . O agente ideal irá desempenhar bem e avaliar todas as suas ações como tendo Advantage igual a 0 e, portanto, com um gradiente igual a 0.

Avaliação de vantagem através da função Value

Lembre-se da definição de vantagem:

Não está claro como aprender explicitamente essa função. Um truque virá ao resgate, o que reduzirá o cálculo da função Advantage ao cálculo da função Value.

Definir $$$\ delta_t ^ V = r_t + V (s_ {t + 1}) - V (s_t)$ - Diferença temporal residual ( TD-residual ). Não é difícil deduzir que essa função se aproxima do Advantage:

Essa mudança conceitualmente complexa provoca uma mudança não tão grande no código. Agora, em vez de avaliar a função Valor, o crítico enviará uma avaliação do Advantage para o treinamento de políticas.

O algoritmo resultante é chamado de Advantage Actor-Critic .

 def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + np.append(values[1:], np.array([0])) return deltas, values 

Os agentes obtidos podem ser observados marcha confiante e uso síncrono dos membros:

Estimativa de Vantagens Generalizadas

Um artigo relativamente recente (2018), " Controle contínuo de alta dimensão usando determinação generalizada de vantagens ", oferece uma avaliação ainda mais eficaz do Advantage por meio da função Value. Reduz ainda mais a variação:

onde:

• $$$\ delta_t ^ V = r_t + V (s_ {t + 1}) - V (s_t)$ - TD residual,
• $$$\ gama$ - fator de desconto (hiperparâmetro),
• $$$\ lambda$ - hiperparâmetro.

A interpretação pode ser encontrada na própria publicação.

Implementação:

 def discount_cumsum(x, coef): # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + discount_factor * np.append(values[1:], np.array([0])) advantage = discount_cumsum(deltas, coef=lambda_factor * discount_factor) return advantage, values 

Ao usar um tamanho de lote pequeno, o algoritmo convergiu para algumas ótimas locais. Aqui, o agente usa uma pata como bengala e o restante empurra:

Aqui, o agente não chegou ao uso de saltos, mas simplesmente mexeu rapidamente nos membros. E você também pode ver como ele se comporta; se ele hesitar, ele se voltará e continuará correndo:

O melhor agente, ele está no começo do artigo. Salto estável, durante o qual todos os membros saem da superfície. A capacidade desenvolvida de equilibrar permite que o agente corrija a trajetória a toda velocidade, se um erro foi cometido:

Armadilhas

O aprendizado de máquina é famoso pela dimensão do espaço de erros que pode ser cometido e obtém um algoritmo completamente inoperante. Mas a RL leva o problema a um nível totalmente novo.

Fonte

Aqui estão algumas das dificuldades encontradas durante o desenvolvimento.

1. O algoritmo é surpreendentemente sensível aos hiperparâmetros. Houve uma mudança na qualidade da aprendizagem ao alterar a taxa de aprendizagem de 3e-4 para 1e-4. E a imagem mudou radicalmente - de um algoritmo completamente não convergente para o melhor que está no vídeo.
2. O tamanho do lote não é o mesmo que em outras áreas da DL. Se na classificação de imagens você puder escolher o tamanho do lote 32-256 e o ​​resultado não for alterado significativamente de aumentá-lo, é melhor levar alguns milhares, 3000 trabalhos para nossa tarefa. E novamente, por falta de convergência em um bom algoritmo.
3. É melhor aprender várias vezes, às vezes com sementes aleatórias não dá sorte.
4. Aprender em um ambiente tão complexo leva muito tempo e o progresso não é uniforme. Por exemplo, o melhor algoritmo aprendido por 8 horas, 3 dos quais mostraram um resultado pior do que uma linha de base aleatória. Portanto, ao testar os algoritmos, é melhor começar com um pequeno, como ambientes de brinquedos da academia.
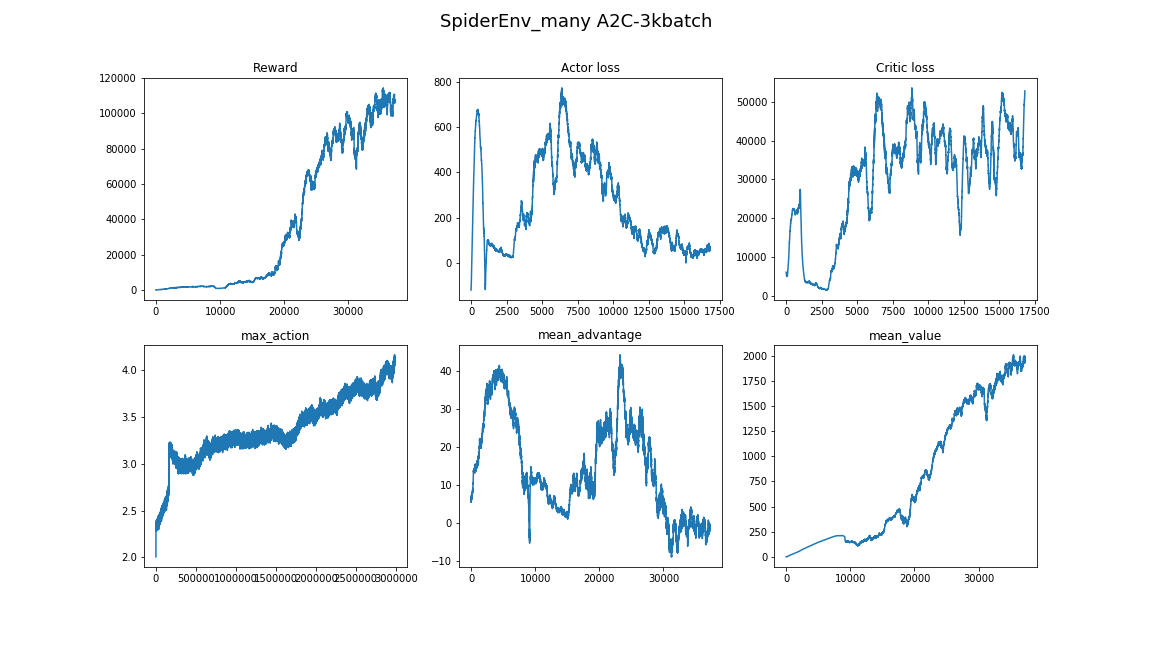
5. Uma boa abordagem para encontrar hiperparâmetros e arquiteturas de modelo seria espiar artigos e implementações relacionadas. (o principal não é treinar novamente)

Você pode aprender mais sobre as nuances do Deep RL neste artigo: O Deep Reforcement Learning ainda não funciona .

Conclusão

O algoritmo resultante resolve de maneira convincente o problema. Função encontrada $$$\ pi: \ R ^ {800} \ to \ R ^ {18}$ , controlando o robô com agilidade e confiança.

Uma continuação lógica será o estudo de parentes próximos dos algoritmos A2C, PPO e TRPO. Eles melhoram a eficiência da amostra , ou seja, tempo de convergência do algoritmo e são capazes de resolver problemas mais complexos. Foi a aleatorização automática de domínio PPO + que montou recentemente o cubo de Rubik em um robô .

Aqui você pode encontrar o código do artigo: repository .

Espero que tenham gostado do artigo e tenham sido inspirados pelo que o Deep Reinforcement Learning pode fazer hoje.

Obrigado pela atenção!

Links úteis:

• Bem-vindo ao Spinning Up in Deep RL!
• CS 294: Aprendizado de reforço profundo, outono de 2017
• CS 285: Aprendizado de reforço profundo, tomada de decisão e controle
• Controle contínuo de alta dimensão usando a determinação generalizada de vantagens
• OpenAI Baselines: implementações de alta qualidade de algoritmos de aprendizado por reforço

Agradecemos a pinkotter , Vambala , andrey_probochkin , pollyfom e suriknik por ajudarem no projeto.
Em particular, Vambala e andrey_probochkin por criar um ambiente legal de MuJoCo.