Olá pessoal! As férias de Ano Novo chegaram ao fim, o que significa que estamos novamente prontos para compartilhar material útil com você. Uma tradução deste artigo foi preparada em antecipação ao lançamento de um novo fluxo no curso "Algoritmos para desenvolvedores" .
Vamos lá!
O método de erro de propagação traseira é provavelmente o componente mais fundamental de uma rede neural. Foi descrito pela primeira vez na década de 1960 e quase 30 anos depois foi popularizado por Rumelhart, Hinton e Williams em um artigo intitulado
"Aprendendo representações por erros de propagação traseira" .
O método é usado para treinar efetivamente uma rede neural usando a chamada regra de cadeia (a regra de diferenciação de uma função complexa). Simplificando, após cada passagem pela rede, a propagação de retorno realiza uma passagem na direção oposta e ajusta os parâmetros do modelo (pesos e deslocamentos).
Neste artigo, gostaria de considerar em detalhes do ponto de vista matemático o processo de aprendizado e otimização de uma rede neural simples de quatro camadas. Acredito que isso ajudará o leitor a entender como a retropropagação funciona, bem como a perceber seu significado.
Definindo um modelo de rede neural
A rede neural de quatro camadas consiste em quatro neurônios na camada de entrada, quatro neurônios nas camadas ocultas e 1 neurônio na camada de saída.
Uma imagem simples de uma rede neural de quatro camadas.Camada de entrada
Na figura, os neurônios roxos representam a entrada. Podem ser quantidades escalares simples ou mais complexas - vetores ou matrizes multidimensionais.
Equação que descreve as entradas xi.O primeiro conjunto de ativações (a) é igual aos valores de entrada. "Ativação" é o valor de um neurônio após a aplicação da função de ativação. Veja abaixo para mais detalhes.
Camadas ocultas
Os valores finais nos neurônios ocultos (na figura verde) são calculados usando entradas ponderadas em zl na camada I e em ativações
I na camada L. Para as camadas 2 e 3, as equações serão as seguintes:
Para l = 2:
Para l = 3:
W
2 e W
3 são os pesos nas camadas 2 e 3 eb
2 eb
3 são as compensações nessas camadas.
As ativações a
2 e a
3 são calculadas usando a função de ativação f. Por exemplo, essa função f é não linear (como
sigmóide ,
ReLU e
tangente hiperbólica ) e permite que a rede estude padrões complexos nos dados. Não vamos nos deter sobre como as funções de ativação funcionam, mas se você estiver interessado, recomendo a leitura deste maravilhoso
artigo .
Se você observar atentamente, verá que todos os x, z
2 , a
2 , z
3 , a
3 , W
1 , W
2 , b
1 eb
2 não têm os índices mais baixos mostrados na figura da rede neural de quatro camadas. O fato é que combinamos todos os valores de parâmetros em matrizes agrupadas por camadas. Essa é uma maneira padrão de trabalhar com redes neurais e é bastante confortável. No entanto, examinarei as equações para que não haja confusão.
Vamos pegar a camada 2 e seus parâmetros como exemplo. As mesmas operações podem ser aplicadas a qualquer camada da rede neural.
W
1 é a matriz de pesos de dimensão
(n, m) , onde
n é o número de neurônios de saída (neurônios na próxima camada) e
m é o número de neurônios de entrada (neurônios na camada anterior). No nosso caso,
n = 2 e
m = 4 .
Aqui, o primeiro número no subscrito de qualquer um dos pesos corresponde ao índice de neurônios na próxima camada (no nosso caso, esta é a segunda camada oculta) e o segundo número corresponde ao índice de neurônios na camada anterior (no nosso caso, essa é a camada de entrada).
x é o vetor de entrada da dimensão (
m , 1), onde
m é o número de neurônios de entrada. No nosso caso,
m = 4.
b
1 é o vetor de deslocamento da dimensão (
n , 1), onde
n é o número de neurônios na camada atual. No nosso caso,
n = 2.
Seguindo a equação para z
2, podemos usar as definições acima de W
1 , x e b
1 para obter a equação z
2 :
Agora observe atentamente a ilustração da rede neural acima:
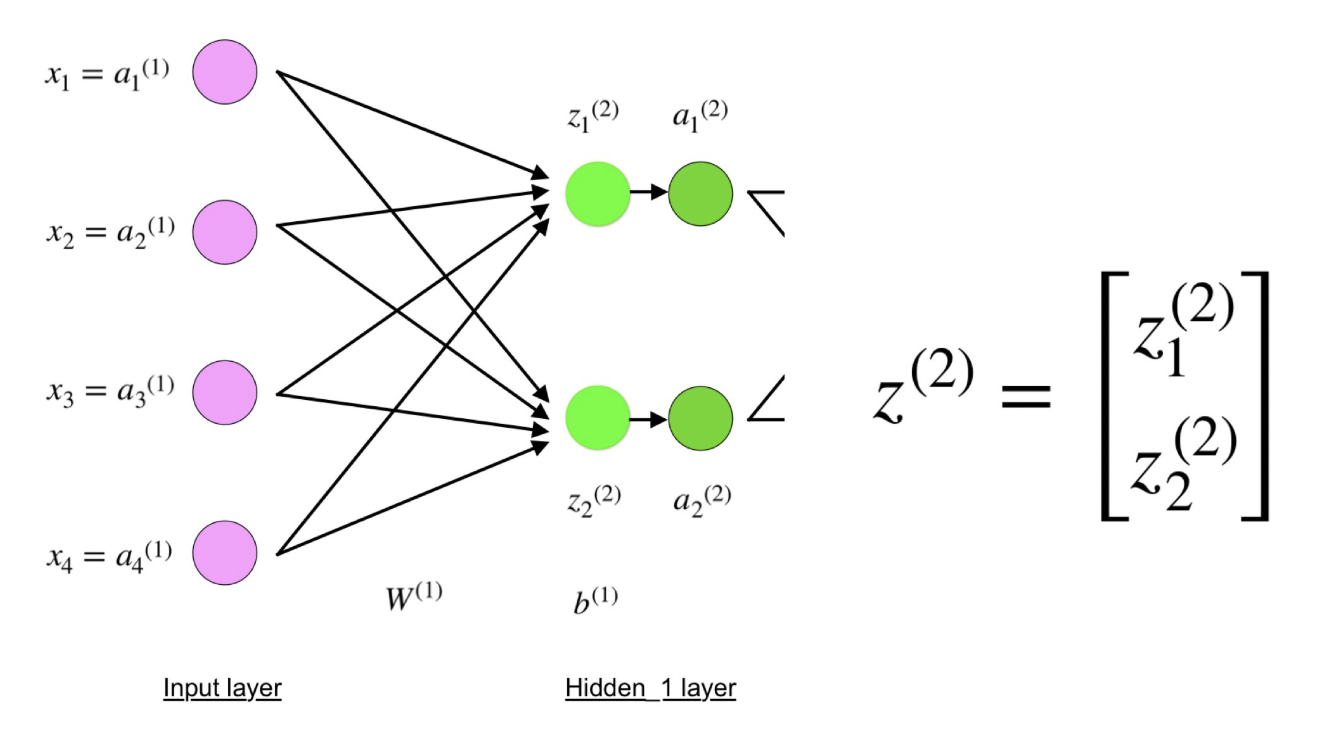
Como você pode ver, z
2 pode ser expresso em termos de z
1 2 e z
2 2 , em que z
1 2 e z
2 2 são as somas dos produtos de cada valor de entrada x
i pelo peso correspondente W
ij 1 .
Isso leva à mesma equação para z
2 e prova que as representações da matriz z
2 , a
2 , z
3 e a
3 são verdadeiras.
Camada de saída
A última parte da rede neural é a camada de saída, que fornece o valor previsto. Em nosso exemplo simples, ele é apresentado na forma de um único neurônio corado em azul e calculado da seguinte forma:
Novamente, usamos a representação matricial para simplificar a equação. Você pode usar os métodos acima para entender a lógica subjacente.
Distribuição e avaliação direta
As equações acima formam uma distribuição direta através da rede neural. Aqui está uma rápida visão geral:
(1) - camada de entrada
(2) - o valor do neurônio na primeira camada oculta
(3) - valor de ativação na primeira camada oculta
(4) - o valor do neurônio na segunda camada oculta
(5) - valor de ativação no segundo nível oculto
(6) - camada de saídaA etapa final na passagem direta é avaliar o valor de saída previsto
s em relação ao valor de saída esperado
y .
A saída y faz parte do conjunto de dados de treinamento (x, y), onde
x é a entrada (como recordamos na seção anterior).
A estimativa entre
s e
y ocorre através da função de perda. Pode ser simples como um
erro padrão ou mais complexo como
entropia cruzada .
Chamamos essa função de perda C e a denotamos da seguinte forma:
Onde o
custo pode ser igual ao erro padrão, entropia cruzada ou qualquer outra função de perda.
Com base no valor de C, o modelo “sabe” quanto seus parâmetros precisam ser ajustados para se aproximar do valor de saída esperado de
y . Isso acontece usando o método de retropropagação.
Propagação traseira de erro e cálculo de gradientes
Com base em um artigo de 1989, o método de retropropagação:
Ajusta constantemente os pesos das conexões na rede para minimizar a medida da diferença entre o vetor de saída real da rede e o vetor de saída desejado .
e
... torna possível criar novas funções úteis que distinguem a retropropagação dos métodos anteriores e mais simples ...Em outras palavras, a retropropagação visa minimizar a função de perda, ajustando os pesos e compensações da rede. O grau de ajuste é determinado pelos gradientes da função de perda em relação a esses parâmetros.
Surge uma pergunta:
por que calcular gradientes ?
Para responder a essa pergunta, primeiro precisamos revisar alguns conceitos de computação:
O gradiente da função C (x
1 , x
2 , ..., x
m ) em x é o
vetor de derivadas parciais de C em
relação a
x .
A derivada da função C reflete a sensibilidade a uma mudança no valor da função (valor de saída) em relação à mudança em seu argumento
x (
valor de entrada ). Em outras palavras, a derivada nos diz em qual direção C. está se movendo.
O gradiente mostra quanto é necessário alterar o parâmetro
x (na direção positiva ou negativa) para minimizar C.
Esses gradientes são calculados usando um método chamado
regra de cadeia.
Para um peso (w
jk )
l, o gradiente é:
(1) Regra da cadeia
(2) Por definição, m é o número de neurônios por camada l - 1
(3) Cálculo derivativo
(4) Valor final
Um conjunto semelhante de equações pode ser aplicado a (b j ) l :
(1) Regra da cadeia
(2) Cálculo derivativo
(3) Valor finalA parte comum em ambas as equações é freqüentemente chamada de "gradiente local" e é expressa da seguinte forma:
Um "gradiente local" pode ser facilmente determinado usando uma regra de cadeia. Não vou pintar esse processo agora.
Os gradientes permitem otimizar os parâmetros do modelo:
Até que o critério de parada seja alcançado, o seguinte é executado:
Algoritmo para otimizar pesos e compensações (também chamado descida de gradiente)
- Os valores iniciais de w e b são selecionados aleatoriamente.
- Epsilon (e) é a velocidade da aprendizagem. Determina o efeito do gradiente.
- w e b são representações matriciais de pesos e compensações.
- A derivada de C em relação a w ou b pode ser calculada usando derivadas parciais de C em relação a pesos ou compensações individuais.
- A condição de término é satisfeita assim que a função de perda é minimizada.
Quero dedicar a parte final desta seção a um exemplo simples no qual calculamos o gradiente C com relação a um peso (w
22 )
2 .
Vamos dar um zoom na parte inferior da rede neural acima mencionada:
Representação visual da retropropagação em uma rede neuralO peso (w
22 )
2 conecta (a
2 )
2 e (z
2 )
2 , portanto, para calcular o gradiente é necessário aplicar a regra da cadeia em (z
2 )
3 e (a
2 )
3 :
O cálculo do valor final da derivada de C a partir de (a
2 )
3 requer conhecimento da função C. Como C depende de (a
2 )
3 , o cálculo da derivada deve ser simples.
Espero que este exemplo tenha conseguido lançar alguma luz sobre a matemática por trás do cálculo de gradientes. Se você quiser saber mais, recomendo que você verifique a série de artigos da PNL de Stanford, em que Richard Socher fornece 4 ótimas explicações para a propagação posterior.
Observação final
Neste artigo, expliquei em detalhes como a propagação retroativa de um erro funciona sob o capô usando métodos matemáticos, como cálculo de gradientes, regra de cadeia etc. O conhecimento dos mecanismos desse algoritmo fortalecerá seu conhecimento de redes neurais e permitirá que você se sinta confortável ao trabalhar com modelos mais complexos. Boa sorte em sua jornada de aprendizado profundo!
Só isso. Convidamos a todos para um webinar gratuito sobre o tema "Árvore de segmentos: simples e rápido" .