SVM Explicação do zero e implementação em python. Análise detalhada do método do vetor de suporte

Olá a todos que escolheram o caminho do ML-Samurai!

Introdução:

Neste artigo, consideramos o método da máquina de vetores de suporte ( Eng. SVM, Máquina de vetores de suporte ) para o problema de classificação. A idéia principal do algoritmo será apresentada, a saída da definição de seus pesos e uma simples implementação de DIY será analisada. No exemplo de um conjunto de dados $$$Íris$ será demonstrada a operação do algoritmo escrito com dados linearmente separáveis ​​/ inseparáveis ​​no espaço $$$R ^ 2$ e visualização de treinamento / prognóstico. Além disso, os prós e os contras do algoritmo, suas modificações serão anunciadas.

Figura 1. Foto de código aberto de uma flor de íris

O problema a ser resolvido:

Vamos resolver o problema da classificação binária (quando houver apenas duas classes). Primeiro, o algoritmo treina objetos do conjunto de treinamento, cujos rótulos de classe são conhecidos antecipadamente. Além disso, o algoritmo já treinado prevê o rótulo da classe para cada objeto da amostra adiada / teste. Os rótulos de classe podem assumir valores $$$Y = \ {- 1, +1 \}$ . Objeto - vetor com sinais N $$$x = (x_1, x_2, ..., x_n)$ no espaço $$$R ^ n$ . Ao aprender, o algoritmo deve criar uma função $$$F (x) = y$ o que leva um argumento $$$x$ - um objeto do espaço $$$R ^ n$ e dá o rótulo da classe $$$y$ .

Palavras gerais sobre o algoritmo:

A tarefa de classificação está relacionada ao ensino com um professor. SVM é um algoritmo de aprendizado com um professor. Visualmente, muitos algoritmos de aprendizado de máquina podem ser encontrados neste artigo de primeira linha (consulte a seção "Mapa do mundo do aprendizado de máquina"). Deve-se acrescentar que o SVM também pode ser usado para problemas de regressão, mas o classificador SVM será analisado neste artigo.

O principal objetivo do SVM como classificador é encontrar a equação de um hiperplano separador
$$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 = 0$ no espaço $$$R ^ n$ , que dividiria as duas classes da melhor maneira possível. Visão geral da transformação $$$F$ instalação $$$x$ ao rótulo da classe $$$Y$ : $$$F (x) = sinal (w ^ Tx-b)$ . Lembraremos que designamos $$$w = (w_1, w_2, ..., w_n), b = -w_0$ . Depois de configurar os pesos do algoritmo $$$w$ e $$$b$ (treinamento), todos os objetos que caem de um lado do hiperplano construído serão previstos como a primeira classe e os objetos que caem do outro lado - a segunda classe.

Função interna $$ existe uma combinação linear de recursos do objeto com os pesos do algoritmo, razão pela qual SVM se refere a algoritmos lineares. Um hiperplano em divisão pode ser construído de maneiras diferentes, mas em pesos SVM $$$w$ e $$$b$ são configurados para que os objetos de classe fiquem o mais longe possível do hiperplano de separação. Em outras palavras, o algoritmo maximiza a diferença ( margem em inglês ) entre o hiperplano e os objetos de classe mais próximos. Tais objetos são chamados vetores de suporte (veja a Fig. 2). Daí o nome do algoritmo.

Figura 2. SVM (a base da figura daqui )

Uma saída detalhada das regras de ajuste da escala SVM:

Para manter o hiperplano divisor o mais longe possível dos pontos de amostra, a largura da tira deve ser máxima. Vetor $$$w$ É o vetor de direção do hiperplano em divisão. A seguir, denotamos o produto escalar de dois vetores como $$$\ langle a, b \ rangle$ ou $$$a ^ Tb$ Vamos encontrar a projeção do vetor cujas extremidades serão os vetores de suporte de diferentes classes no vetor de direção do hiperplano. Esta projeção mostra a largura da faixa divisória (veja a Fig. 3):

Figura 3. A saída das regras para definir as escalas (a base da figura daqui )

A margem do objeto x do limite da classe é o valor $$$M = y (w ^ Tx-b)$ . O algoritmo comete um erro no objeto se e somente se o recuo $$$M$ negativo (quando $$$y$ e $$$(w ^ Tx-b)$ caracteres diferentes). Se $$$M ∈ (0, 1)$ , o objeto cai dentro da faixa divisória. Se $$$M> 1$ , o objeto x é classificado corretamente e está localizado a alguma distância da faixa divisória. Escrevemos esta conexão:

O sistema resultante é a configuração padrão do SVM com um SVM de margem fixa, quando nenhum objeto tem permissão para entrar na banda de separação. É resolvido analiticamente através do teorema de Kuhn-Tucker. O problema resultante é equivalente ao problema duplo de encontrar o ponto de sela da função Lagrange.

$$$$ display $$ \ left \ {\ begin {array} {ll} (w ^ Tw) / 2 \ rightarrow min & \ textrm {} \\ y (w ^ Tx-b) \ geqslant 1 & \ textrm {} \ end {array} \ right. $$ display $$

Tudo isso é bom, desde que nossas classes sejam linearmente separáveis. Para que o algoritmo possa trabalhar com dados linearmente inseparáveis, vamos transformar um pouco nosso sistema. Deixe o algoritmo cometer erros nos objetos de treinamento, mas ao mesmo tempo tente manter menos erros. Introduzimos um conjunto de variáveis ​​adicionais $$$\ xi _i> 0$ caracterizando a magnitude do erro em cada objeto $$$x_i$ . Introduzimos uma penalidade pelo erro total no funcional minimizado:

$$$$ display $$ \ left \ {\ begin {array} {ll} (w ^ Tw) / 2 + \ alpha \ sum \ xi _i \ rightarrow min & \ textrm {} \\ y (w ^ Tx_i-b) \ geqslant 1 - \ xi _i & \ textrm {} \\ \ xi _i \ geqslant0 & \ textrm {} \ end {array} \ right. $$ display $$

Vamos considerar o número de erros de algoritmo (quando M <0). Chame de penalidade . A penalidade para todos os objetos será igual à quantidade de multas para cada objeto $$$x_i$ onde $$$[M_i <0]$ - função de limiar (ver Fig. 4):

$$$$ display $$ [M_i <0] = \ left \ {\ begin {array} {ll} 1 & \ textrm {if} M_i <0 \\ 0 & \ textrm {if} M_i \ geqslant 0 \ end {array} \ right. $$ display $$

Em seguida, tornamos a penalidade sensível à magnitude do erro e, ao mesmo tempo, introduzimos uma penalidade por aproximar o objeto do limite da classe:

Ao adicionar à expressão de penalidade, o termo $$$\ alpha (w ^ Tw) / 2$ obtemos a função clássica de perda de SVM com gap suave ( SVM de margem flexível ) para um objeto:

$$$Q$ - função de perda, também é uma função de perda. É isso que minimizaremos com a ajuda da descida gradiente na implementação das mãos. Derivamos as regras para alterar pesos, onde $$$\ eta$ - degrau de descida:

$$exibição $$ $$ \ bigtriangledown Q = \ left \ {\ begin {array} {ll} \ alpha w-yx & \ textrm {if} yw ^ Tx <1 \\ \ alpha w & \ textrm {if} yw ^ Tx \ geqslant 1 \ end {array} \ right. $$ display $$

Possíveis perguntas em entrevistas (baseadas em eventos reais):

Após perguntas gerais sobre o SVM: Por que o Hinge_loss está maximizando a liberação? - primeiro, lembre-se de que um hiperplano muda de posição quando os pesos mudam $$$w$ e $$$b$ . Os pesos do algoritmo começam a mudar quando os gradientes da função de perda não são iguais a zero (geralmente dizem: "fluxo de gradientes"). Portanto, selecionamos especialmente uma função de perda, na qual gradientes começam a fluir no momento certo. $$$Perda de dobradiça$ é assim: $$$H = max (0,1-y (w ^ Tx))$ . Lembre-se de que a folga $$$m = y (w ^ Tx)$ . Quando a diferença $$$m$ grande o suficiente ( $$$1$ ou mais) expressão $$$(1 m)$ torna-se menor que zero e $$$H = 0$ (portanto, os gradientes não fluem e o peso do algoritmo não muda de forma alguma). Se o intervalo m for suficientemente pequeno (por exemplo, quando um objeto cair na faixa de separação e / ou negativo (se a previsão de classificação estiver incorreta), Hinge_loss se tornará positivo ( $$$H> 0$ ), os gradientes começam a fluir e os pesos do algoritmo mudam. Resumindo: os gradientes fluem em dois casos: quando o objeto de amostra caiu dentro da faixa de separação e quando o objeto é classificado incorretamente.

Para verificar o nível de uma língua estrangeira, perguntas semelhantes são possíveis: Quais são as semelhanças e diferenças entre LogisticRegression e SVM? - em primeiro lugar, falaremos sobre semelhanças: ambos os algoritmos são algoritmos de classificação linear no aprendizado supervisionado. Algumas semelhanças estão em seus argumentos de funções de perda: $$$log (1 + exp (-y (w ^ Tx)))$ para logreg e $$$max (0,1-y (w ^ Tx))$ para SVM (veja a figura 4). Podemos configurar os dois algoritmos usando a descida em gradiente. A seguir, vamos falar sobre as diferenças: o SVM retorna o rótulo da classe do objeto, diferentemente do LogReg, que retorna a probabilidade de associação à classe. O SVM não pode funcionar com rótulos de classe $$$\ {0,1 \}$ (sem renomear classes), ao contrário do LogReg (diferença de perda do LogReg para $$$\ {0,1 \}$ : $$$-ylog (p) - (1-y) log (1-p)$ onde $$$y$ - etiqueta de classe real, $$$p$ - retorno do algoritmo, probabilidade de pertencer ao objeto $$$x$ para a aula $$$\ {1 \}$ ) Mais do que isso, podemos resolver o problema SVM de margem rígida sem descida do gradiente. A tarefa de pesquisar vetores de suporte é reduzida para pesquisar o ponto de sela na função Lagrange - esta tarefa refere-se apenas à programação quadrática.

import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14}); 

Figura 4. Funções de perda

Implementação simples do SVM clássico de margem suave:

Atenção! Você encontrará um link para o código completo no final do artigo. Abaixo estão os blocos de código retirados do contexto. Alguns blocos só podem ser iniciados após o trabalho dos blocos anteriores. Sob muitos blocos, serão colocadas fotos que mostram como o código colocado acima funcionou.

 import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): #    #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l 

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended class CustomSVM(object): __class__ = "CustomSVM" __doc__ = """ This is an implementation of the SVM classification algorithm Note that it works only for binary classification ############################################################# ###################### PARAMETERS ###################### ############################################################# etha: float(default - 0.01) Learning rate, gradient step alpha: float, (default - 0.1) Regularization parameter in 0.5*alpha*||w||^2 epochs: int, (default - 200) Number of epochs of training ############################################################# ############################################################# ############################################################# """ def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) def predict(self, X:np.array) -> np.array: y_pred = [] X_extended = add_bias_feature(X) for i in range(len(X_extended)): y_pred.append(np.sign(np.dot(self._w,X_extended[i]))) return np.array(y_pred) def hinge_loss(self, x, y): return max(0,1 - y*np.dot(x, self._w)) def soft_margin_loss(self, x, y): return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w) 

Consideramos em detalhes a operação de cada bloco de linhas:

1) crie uma função add_bias_feature (a) , que estenda automaticamente o vetor de objetos, adicionando o número 1 ao final de cada vetor, o que é necessário para “esquecer” o termo livre b. Expressão $$$w ^ Tx-b$ equivalente à expressão $$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 * 1$ . Assumimos condicionalmente que a unidade é o último componente do vetor para todos os vetores x, e $$$w_0 = -b$ . Agora definindo os pesos $$$w$ e $$$w_0$ Vamos produzir ao mesmo tempo.

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended 

2) então descreveremos o próprio classificador. Ele tem as funções de inicializar init () , ajuste de aprendizado () , previsão de previsão () , localização da perda da função hinge_loss () e localização da perda total da função do algoritmo clássico com uma lacuna suave soft_margin_loss () .

3) na inicialização, são introduzidos 3 hiperparâmetros: _etha - passo de descida do gradiente ( $$$\ eta$ ), _alpha - coeficiente de velocidade de redução proporcional do peso (antes do termo quadrático na função de perda) $$$\ alpha$ ), _epochs - o número de eras de treinamento.

  def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None 

4) durante o treinamento para cada era da amostra de treinamento (X_train, Y_train), pegaremos um elemento da amostra, calcularemos a diferença entre esse elemento e a posição do hiperplano em um determinado momento. Além disso, dependendo do tamanho dessa lacuna, alteraremos o peso do algoritmo usando o gradiente da função de perda $$$Q$ . Ao mesmo tempo, calcularemos o valor dessa função para cada época e quantas vezes alteramos os pesos por época. Antes de iniciar o treinamento, garantiremos que não mais do que dois rótulos de classe diferentes realmente entrem na função de aprendizado. Antes de configurar a balança, ela é inicializada usando a distribuição normal.

  def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) 

Verificando a operação do algoritmo escrito:

Verifique se nosso algoritmo escrito funciona em algum tipo de conjunto de dados de brinquedo. Pegue o conjunto de dados Iris. Vamos preparar os dados. Indique as classes 1 e 2 como $$$+ 1$ e classe 0 como $$$-1$ . Usando o algoritmo PCA (explicação e aplicação aqui ), reduzimos de maneira ideal o espaço de 4 atributos para 2 com perda mínima de dados (será mais fácil observar o treinamento e o resultado). Em seguida, dividiremos em uma amostra de treinamento (trem) e uma amostra atrasada (validação). Vamos treinar na amostra de treinamento, prever e verificar os diferidos. Escolhemos os fatores de aprendizado para que a função de perda caia. Durante o treinamento, examinaremos a função de perda do treinamento e a amostragem atrasada.

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

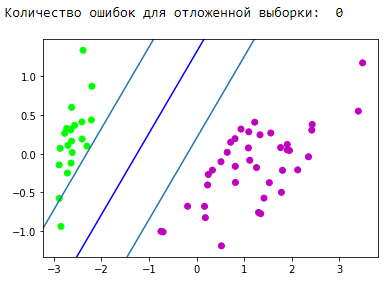
Ótimo! Nosso algoritmo manipulou dados linearmente separáveis. Agora faça separar as classes 0 e 1 da classe 2:

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors[:150]) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

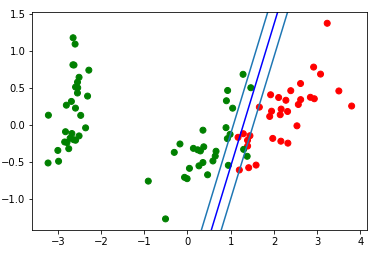
Vejamos o gif, que mostrará como a linha divisória mudou de posição durante o treinamento (apenas 500 quadros para alterar pesos. Os primeiros 300 em sequência. Próximas 200 peças para cada 130º quadro):

 import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 return im fig = plt.figure() ims = [] for i in range(500): if i<=300: k = i else: k = (i-298)*130 im = one_image(svm.history_w[k], X_train, Y_train) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True, repeat_delay=500) writer = PillowWriter(fps=20) ani.save("my_demo.gif", writer='imagemagick') 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

Endireitando espaços

É importante entender que, em problemas reais, não haverá um caso simples com dados linearmente separáveis. Para trabalhar com esses dados, foi proposta a ideia de mudar para outro espaço, onde os dados serão linearmente separáveis. Tal espaço é chamado de retificador. Espaços de retificação e kernels não serão afetados neste artigo. Você pode encontrar a teoria matemática mais completa na 14,15,16 sinopse de E. Sokolov e nas palestras de K.V. Vorontsov .

Usando o SVM do sklearn:

De fato, quase todos os algoritmos clássicos de aprendizado de máquina são escritos para você. Vamos dar um exemplo do código, pegaremos o algoritmo da biblioteca sklearn .

 from sklearn import svm from sklearn.metrics import recall_score C = 1.0 # = self._alpha in our algorithm model1 = svm.SVC(kernel='linear', C=C) #model1 = svm.LinearSVC(C=C, max_iter=10000) #model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C) #model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C) model1.fit(X_train, Y_train) y_predict = model1.predict(X_test) print(recall_score(Y_test, y_predict, average=None)) 

Prós e contras do SVM clássico:

Prós:

1. funciona bem com grande espaço de recursos;
2. funciona bem com pequenos dados;
3. Portanto, o algoritmo descobre que maximiza a banda divisória, que, como um airbag, pode reduzir o número de erros de classificação;
4. como o algoritmo se reduz à resolução do problema de programação quadrática em um domínio convexo, esse problema sempre tem uma solução única (o hiperplano de separação com certos hiperparâmetros do algoritmo é sempre o mesmo).

Contras:

1. longo tempo de treinamento (para grandes conjuntos de dados);
2. instabilidade do ruído: os valores discrepantes nos dados de treinamento se tornam objetos de intrusão de referência e afetam diretamente a construção de um hiperplano de separação;
3. métodos gerais para construir núcleos e retificar espaços mais adequados para um problema específico no caso de inseparabilidade linear de classes não são descritos. Selecionar transformações úteis de dados é uma arte.

Aplicação SVM:

A escolha de um ou outro algoritmo de aprendizado de máquina depende diretamente das informações obtidas durante a mineração de dados. Mas, em termos gerais, as seguintes tarefas podem ser distinguidas:

• tarefas com um pequeno conjunto de dados;
• tarefas de classificação de texto. O SVM fornece uma boa linha de base ([pré-processamento] + [TF-iDF] + [SVM]), a precisão da previsão resultante está no nível de algumas redes neurais convolucionais / recorrentes (eu recomendo tentar esse método para consolidar o material). Um excelente exemplo é dado aqui, "Parte 3. Um exemplo de um dos truques que ensinamos" ;
• para muitas tarefas com dados estruturados, o link [engenharia de recursos] + [SVM] + [kernel] "still cake";
• Como a perda de dobradiça é considerada muito rápida, ela pode ser encontrada no Vowpal Wabbit (por padrão).

Modificações do algoritmo:

Existem várias adições e modificações no método do vetor de suporte, com o objetivo de eliminar certas desvantagens:

• Relevance Vector Machine (RVM)
• SVM de 1 norma (LASSO SVM)
• SVM duplamente regularizado (ElasticNet SVM)
• Máquina de recursos de suporte (SFM)
• Máquina de recursos de relevância (RFM)

Fontes adicionais no SVM:

1. Palestras de texto de K.V. Vorontsov
2. Resumos de E. Sokolov - 14.15.16
3. Fonte legal por Alexandre Kowalczyk
4. Em um habr existem 2 artigos dedicados ao svm:
   
   • Ano 2010
   • 2018 ano
5. No github, posso destacar duas implementações legais de SVM nos seguintes links:
   
   • MLAlgoritmos de um desenvolvedor doméstico
   • ML-From-Scratch

Conclusão:

Muito obrigado pela atenção! Ficaria muito grato por quaisquer comentários, feedback e dicas.
Você encontrará o código completo deste artigo no meu github .

ps Obrigado yorko por dicas sobre como suavizar cantos. Agradecimentos a Aleksey Sizykh - um departamento de física e tecnologia que investiu parcialmente no código.