Boa tarde
Como prometido no meu primeiro artigo , quero familiarizá-lo com um dos métodos para resolver o sistema de equações diofantinas. O objetivo do artigo é familiarizar outros leitores com essa técnica e transmiti-la de maneira mais ou menos compreensível.
Considere um sistema de duas equações diofantinas
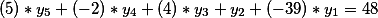
e

Encontramos todas as soluções possíveis para a primeira equação. Como você pergunta? Certamente existem métodos diferentes, mas vou compartilhar em um dos artigos a seguir como resolveria um problema semelhante. Agora, assumimos que a solução geral tem a forma

Como verificar se não estou mentindo?
Basta recordar o cálculo da matriz e multiplicar o vetor de valores da nossa primeira equação diofantina (sem termo livre) pela matriz de todos os coeficientes .

obteve como resultado o valor do termo livre e, portanto, os cálculos estão corretos
O próximo passo é substituir nossa solução comum.

na segunda equação

O procedimento é o mesmo: multiplicamos o vetor dos coeficientes da segunda equação pela solução geral da primeira
nós obtemos este resultado
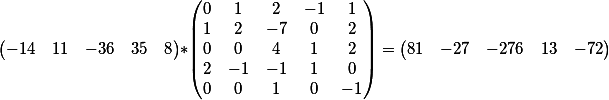
isto é, temos uma equação da forma
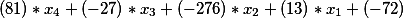
No lado direito da segunda equação diofantina, como havia um termo livre igual a -335, permaneceu, ou seja, nossa solução final nesta fase tem a forma
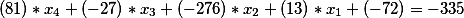
Ou movendo os membros gratuitos para a direita, obtemos
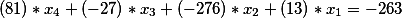
Então, nós temos a próxima equação diofantina. Vamos encontrar sua solução geral e testá-la pela verdade.

isto é, a solução geral é
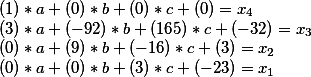
E agora estamos fazendo a transformação inversa (que seja chamada assim). Ou seja, o sistema

Em vez de x desconhecido, substituímos o que aconteceu na última etapa
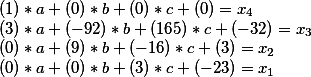
No cálculo da matriz, isso é resolvido multiplicando uma matriz por outra.
Porém, com a primeira matriz, é necessário executar um determinado procedimento: remova (temporariamente) a última coluna com membros livres, pois esse parâmetro não participa da multiplicação e o utilizará posteriormente.
O resultado da multiplicação de duas matrizes gera
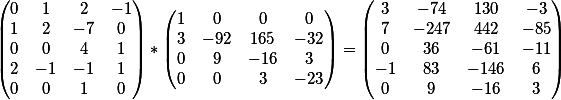
a matriz
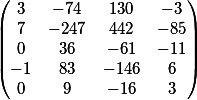
A última coluna são os membros livres deste sistema.
Levamos em conta a coluna que foi temporariamente excluída antes da multiplicação e os adicionamos
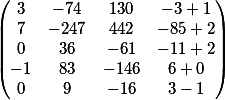
nossa resposta final em forma de matriz
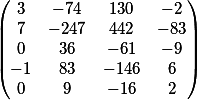
Confira?
O produto vetorial dos coeficientes da primeira equação e da matriz
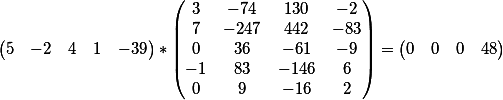
e o produto vetorial dos coeficientes da segunda equação e da matriz
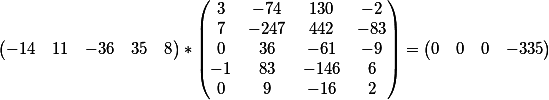
Como você pode ver, o resultado coincide com o termo livre de cada uma das equações.
Assim, a solução geral tem a forma
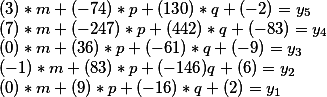
onde m, p, q - pode assumir qualquer valor inteiro
De maneira tão direta, é possível resolver equações diofantinas lineares mais complexas. Uma calculadora verdadeira foi criada após esse algoritmo; essa calculadora realmente não gosta quando ocorrem zeros em vez dos valores nos coeficientes da primeira equação do sistema inicial. Mas esse é um problema da minha implementação específica desse algoritmo.
No próximo tópico, descreverei como criar equações diofantinas usando a matriz da solução geral. A tarefa geralmente é banal e é executada em uma ação, mas de repente alguém não sabe.
Ficaria muito grato pelos comentários, feedback e sugestões.