Durante séculos, os pesquisadores procuraram exemplos de situações nas quais as equações de Euler para a hidrodinâmica de um fluido ideal se mostram incorretas. E, finalmente, os matemáticos encontraram esse exemplo.
Por muitos anos, matemáticos suspeitaram que, sob certas condições,
as equações de Euler se recusariam a trabalhar. No entanto, eles não conseguiram descrever o cenário específico em que isso ocorre. Até hoje.
Essas equações são uma descrição matemática idealizada do movimento de fluidos. Dentro de certas suposições, eles modelam a propagação de ondas em um lago ou a infiltração de melaço de uma lata. Eles devem ser capazes de descrever o movimento de qualquer líquido em qualquer condição - e por mais de dois séculos, foi.
No entanto, novas evidências demonstram que, sob certas condições, essas equações ainda se recusam a funcionar.
"Há um ano e meio, eu diria que não esperava ver esse desenvolvimento, mesmo durante a minha vida", disse
Tarek Elgindi , matemático da Universidade da Califórnia em San Diego, autor de um novo trabalho.
Elgindi provou a existência de falhas nas equações de Euler em dois trabalhos publicados em 2019 - ele próprio escreveu
April e
outubro - em colaboração com
Tejeddin Gole e
Nader Masmudi . O trabalho transformou mais de um século de suposições sobre essas famosas equações para líquidos.
"Acho que essa é uma conquista maravilhosa e maravilhosa", disse
Peter Constantine , matemático da Universidade de Princeton.
O trabalho de Elgindi não inaugura o fim das equações de Euler. Prova que, sob certas condições, as equações parecem superaquecer e começam a dar disparates. Mas em condições mais realistas, as equações até agora permanecem invulneráveis.
No entanto, a exceção encontrada por Elgindi surpreendeu os matemáticos, pois ocorre em condições nas quais, como se pensava anteriormente, a equação deveria funcionar de qualquer maneira.
"Em geral, parece-me que as pessoas ficam surpresas com o exemplo dado por Tarek", disse
Vlad Vikol , matemático da Universidade de Nova York.
Como as equações de Euler correram
Leonhard Euler derivou as equações para líquidos que agora levam seu nome em 1757. Eles descrevem a evolução de um fluido ao longo do tempo, assim como as equações de Newton descrevem o movimento de uma bola de bilhar em uma mesa.
Mais precisamente, essas equações denotam o movimento instantâneo de partículas infinitesimais de um líquido. Sua descrição inclui a velocidade da partícula (com que rapidez e em que direção ela se move) e uma quantidade conectada a ela como
vorticidade (com que rapidez a partícula gira da maneira de um topo e em que direção).
Toda essa informação forma inteiramente um "campo de velocidade", um instantâneo do movimento do fluido em um determinado ponto no tempo. As equações de Euler começam com o campo de velocidade inicial e preveem como ele mudará a qualquer momento no futuro.
Tarek ElgindiAs equações de Euler não descrevem o fluido do mundo real literalmente. Isso inclui várias suposições não físicas. Por exemplo, eles funcionam apenas se os fluxos internos no fluido não criarem atrito, movendo-se um em relação ao outro. Também se supõe a incompatibilidade de líquidos, ou seja, de acordo com as regras das equações de Euler, é impossível comprimir um líquido, colocando-o em um espaço de volume menor do que o necessário.
"Este modelo pode ser imaginado como um mundo idealizado e as equações como as regras para o movimento deste mundo", escreveu-nos
Vladimir Sverak, da Universidade de Minnesota, por e-mail.
Essas condições incomuns permitiram ao matemático e físico John von Neumann afirmar, brincando, que essas equações simulam o comportamento da “água seca”. Para simular um fluido mais realista que sofre atrito interno (a chamada viscosidade), os pesquisadores usam
as equações de Navier-Stokes .
As equações de Euler são muito idealizadas. O atrito está presente em líquidos reais ”, disse Konstantin.
Mas, ao mesmo tempo, as equações de Euler ainda ocupam um lugar respeitado na ciência. Os pesquisadores gostariam de saber se essas equações funcionam claramente na estrutura desse mundo idealizado, sem atrito e compressão - isto é, se podem descrever todos os estados futuros de todas as possíveis versões iniciais dos campos de velocidade. Ou, em outras palavras: existe um movimento tão fluido que essas equações não podem modelar?
“No fundo, a pergunta é simples: essas equações sempre funcionam?”, Disse Sverak.
Em teoria, substituindo os valores do estado atual do líquido pelas equações, você obterá quantidades exatas para descrever seu estado futuro. Em seguida, você pode novamente substituir esses novos valores nas equações e estender sua previsão. E geralmente um processo semelhante pode ser continuado por qualquer período de tempo no futuro.
No entanto, também é possível que, em condições muito raras, as equações quebrem. Eles podem estalar, estufar, produzir valores de saída adequados para o papel de futuros parâmetros de entrada e, de repente, produzir um valor que não é adequado para eles. Nesses casos, os matemáticos dizem que as equações "correram".
Se as equações de Euler correm, será porque elas começam a aumentar a velocidade ou a vorticidade do ponto de alguma maneira não natural. Esse ganho será tão forte que, em um tempo finito, a velocidade ou o vórtice de um ponto se torna infinito. E assim que as equações derem um valor infinito, elas irão quebrar e parar de descrever quaisquer condições ambientais no futuro. Isso ocorre porque geralmente é impossível realizar cálculos com valores infinitos - isso é o mesmo que dividir por zero (a propósito, os valores de velocidade nesse caso excederão a velocidade da luz - embora no mundo idealizado do modelo isso não seja o pior).
Esses significados infinitos fatídicos são chamados de "singularidades". Quando os matemáticos perguntam: "As equações de Euler sempre funcionam?", Na verdade perguntam "existem cenários em que as equações de Euler dão singularidades?"
Muitos matemáticos acreditam que, no entanto, até o momento, eles não conseguiram encontrar um cenário específico no qual as equações realmente explodissem.
"Havia um sentimento de que Euler estava tentando evitar a singularidade e, até recentemente, ele conseguiu", disse Konstantin.
O novo trabalho não demonstra como as equações dão singularidades sob condições nas quais os matemáticos estão mais interessados. No entanto, até agora esse resultado chegou mais perto da meta do que o resto. E para isso, Elgindi considerou um modelo simplificado de movimento de fluidos.
Reduzindo a complexidade
Os matemáticos têm muitas maneiras diferentes de reduzir a complexidade do movimento de fluidos, cuja simulação utiliza as equações de Euler. Muitos dos resultados mais interessantes, semelhantes aos alcançados por Elgindi, incluem uma demonstração de quanto você pode simplificar o comportamento do fluido - isto é, quanto você pode simplificar os dados substituídos nas equações - enquanto ainda é capaz de dizer algo significativo sobre as próprias equações.
Em um fluido tridimensional real, como a água em uma lagoa, qualquer partícula tem três eixos possíveis para o movimento: o eixo x (esquerda-direita), o eixo y (de cima para baixo) e o eixo z (de frente para trás). Muita liberdade de movimento. Além disso, o movimento de partículas em uma parte do líquido não estará necessariamente fortemente associado ao movimento de partículas em outra parte.
"Você precisa acompanhar demais", disse Elgindi.
No novo artigo, Elgindi simplifica o trabalho para as equações de Euler. Requer que o líquido seja simétrico ao longo do eixo z, o que geralmente não é encontrado em líquidos reais. Devido à simetria, fica mais fácil calcular o campo de velocidade, pois é sabido que os pontos nos dois lados do eixo z são simétricos em espelho. Portanto, se você conhece a velocidade ou a vorticidade de um ponto, basta alterar o sinal desses valores e obter esses valores para outro ponto.
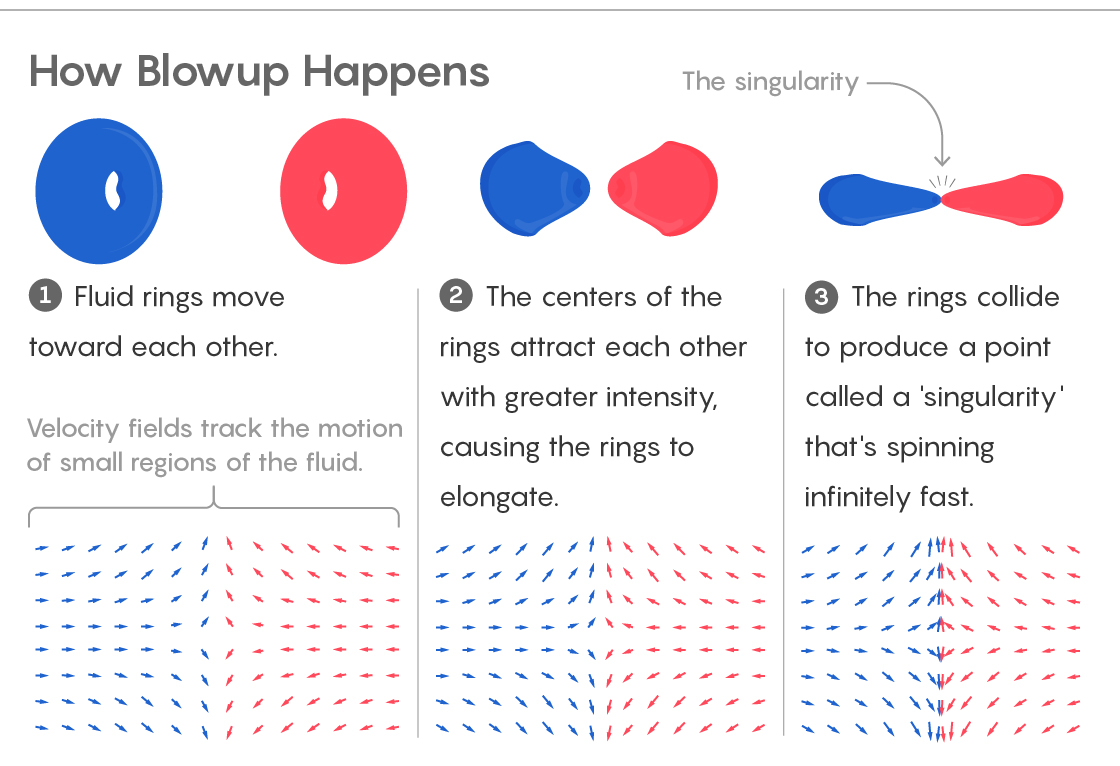1) Os fluidos se movem em direção. Os campos de velocidade acompanham o movimento de pequenas seções de fluido.
2) Os centros dos anéis são atraídos, o que faz com que os anéis se estiquem.
3) Os anéis colidem, criando um ponto de "singularidade", girando em velocidade infinita.Também limita o possível movimento de pontos no fluido. As partículas podem ser movidas ao longo do eixo z, para longe dele ou para ele. Eles não podem girar em torno do eixo z. Os matemáticos dizem que não existem banheiras de hidromassagem nesses líquidos.
"Isso reduz a tarefa para bidimensional", disse Elgindi.
Finalmente, Elgindi impõe mais algumas condições aos dados iniciais introduzidos nas equações de Euler. Em certo sentido, esses dados são mais difíceis do que aqueles que descrevem fluidos reais e aumentam a probabilidade de formação de singularidades.
Na vida real, se você se mover de um ponto para outro, localizado muito perto dele, as velocidades desses dois pontos serão quase iguais. Os vórtices desses dois pontos também devem ser muito semelhantes. Os matemáticos dizem que os campos de velocidade com essa propriedade são "suaves", ou seja, os valores neles mudam gradualmente - ou suavemente - quando se deslocam de um ponto para outro. Sem alterações rápidas.
Mas no caso da descrição do líquido da Elgindi, tudo é diferente.
"A reviravolta nos dados de Tarek pode mudar muito", disse Vikol. "Os pontos próximos podem ter vórtices muito diferentes."
Pode parecer que as simplificações de Elgindi se afastam muito do comportamento de líquidos reais para serem úteis. No entanto, eles ainda são muito menos rígidos do que muitos dos cenários simplificados em que os cientistas consideravam anteriormente as equações de Euler. De fato, Elgindi até mostrou que sob essas condições simplificadas - mas não demais -, as equações de Euler começam a produzir resultados muito inesperados.
Fim do jogo
Para entender a descoberta de Elgindi, imagine um recipiente de água. Este não é um exemplo exato, pois o trabalho de Elgindi considera líquidos que não têm limites, isto é, voando como uma bolha em gravidade zero. Mas, para visualizar o roteiro, que está no centro de seu trabalho, será útil arrumar a água no tanque. Embora as hipóteses matemáticas mais importantes - e as mais difíceis de provar - digam respeito a líquidos sem limites.
Imagine dois grossos anéis de água localizados em diferentes extremidades do tanque. Eles formam pequenos funis, como redemoinhos - distúrbios organizados dentro do fluido. Fenômenos semelhantes são encontrados na natureza e são semelhantes aos anéis de fumaça que fumantes experientes podem emitir.
Agora imagine como dois anéis opostos se juntam.
Durante a abordagem, as equações de Euler funcionam normalmente, contando os campos de velocidade que descrevem o fluido a cada momento no tempo. Mas quando se aproximam o suficiente, as equações começam a produzir resultados muito estranhos.
Eles mostram como os anéis começam a ser atraídos um pelo outro cada vez mais - e os pontos centrais dos anéis são atraídos um pelo outro ainda mais do que pelas partes externas. Como resultado, os anéis são estendidos e começam a parecer um funil. E quanto mais os centros dos anéis se aproximam, mais sua velocidade aumenta. E então eles colidem.
E se, nesse momento, você observar o campo de velocidade que descreve a colisão, poderá ver que, com esse conjunto de suposições em toda a história das equações de Euler, ninguém viu: a singularidade. Elgindi provou que as equações de Euler fornecem velocidade infinita no ponto de colisão. O jogo acabou.
"A forma clássica da equação quebra", disse Elgindi. "Depois disso, não está claro o que está acontecendo."
O resultado tem suas limitações. Ou seja, é impossível extrapolar o comportamento das equações de Euler em condições completamente "suaves" com base nesse resultado. Os matemáticos de algumas décadas atrás provaram que, em condições "suaves", o cenário considerado por Elgindi não produzirá uma singularidade.
No entanto, o restante de seu resultado muda completamente a visão dos matemáticos sobre essas antigas equações.
Antes do trabalho de Elgindi, os matemáticos não podiam provar a existência de qualquer situação em um fluido sem fronteiras, em que as equações de Euler funcionam por algum tempo (enquanto os anéis se juntam), mas não infinitamente. Em todos os trabalhos anteriores, os matemáticos descobriram que, se as equações funcionam basicamente, elas sempre funcionam.
"Este é um resultado muito notável, porque prova a presença de singularidades no cenário, que chamamos de 'definido corretamente'". Faz sentido, mas ao mesmo tempo chegamos a uma singularidade em um tempo finito ”, disse Konstantin.
Muitas gerações de cientistas têm procurado um ponto fraco nas equações de Euler. E finalmente - com algumas reservas - o matemático o encontrou.