Por que a classificação rápida é realmente lenta? Novo método de classificação de matriz

Muitos programadores pensam que o Quick Sort é o algoritmo mais rápido de todos. Isto é parcialmente verdade. Mas ele funciona muito bem apenas se o elemento de suporte for selecionado corretamente ( a complexidade é O (n log n) ). Caso contrário, o comportamento assintótico será aproximadamente o mesmo que o da bolha ( ou seja, O (n ² ) ).
Ao mesmo tempo, se a matriz já estiver classificada, o algoritmo ainda funcionará não mais rápido que O (n log n)

Com base nisso, decidi escrever meu próprio algoritmo para classificar uma matriz que funcionaria melhor que o quick_sort. E se a matriz já estiver classificada, não a execute várias vezes, como é o caso de muitos algoritmos.

“Era noite, não havia o que fazer” - Sergei Mikhalkov.

Requisitos:

1. Melhor caso O (n)
2. O caso médio de O (n log n)
3. Pior caso O (n log n)
4. Em média, mais rápido que a classificação rápida

Agora vamos colocar tudo em ordem

Para que nosso algoritmo sempre funcione rapidamente, é necessário que, no caso médio, o comportamento assintótico seja pelo menos O (n log n) e, na melhor das hipóteses, O (n). Todos sabemos muito bem que, na melhor das hipóteses, a classificação por inserção funciona de uma só vez. Mas, na pior das hipóteses, ela terá que percorrer a matriz quantas vezes houver elementos nela.

Informações preliminares

int* glue(int* a, int lenA, int* b, int lenB) { int lenC = lenA + lenB; int* c = new int[lenC]; //   int indx_a = 0; int indx_b = 0; int i = 0; for (; i < lenC; ++i) { if (indx_a < lenA) { if (indx_b < lenB) { //     c[i] = (a[indx_a] < b[indx_b]) ? a[indx_a++] : b[indx_b++]; continue; } //      while (indx_a < lenA) c[i++] = a[indx_a++]; } else //      while (indx_b < lenB) c[i++] = b[indx_b++]; break; } return c; } 

 void glueDelete(int*& arr, int*& a, int lenA, int*& b, int lenB) { if (lenA == 0) { //    delete[] a; //     arr = b; //     return; } if (lenB == 0) { //    delete[] b; //     arr = a; //     return; } int *copy = glue(a, lenA, b, lenB); //  delete[]a; //    delete[]b; //    arr = copy; //   } 

 void insertionSort(int*& arr, int lo, int hi) { for (int i = lo + 1; i <= hi; ++i) for (int j = i; j > 0 && arr[j - 1] > arr[j]; --j) swap(arr[j - 1], arr[j]); } 

Versão inicial do algoritmo (não otimizada):

A idéia principal do algoritmo é a chamada busca pelo máximo (e mínimo). Em cada iteração, selecione um elemento da matriz. Se for maior que o máximo anterior, adicione este elemento ao final da seleção. Caso contrário, se for menor que o mínimo anterior, adicionamos esse elemento ao início. Caso contrário, coloque em uma matriz separada.

A função de entrada pega uma matriz e o número de elementos nessa matriz

 void FirstNewGeneratingSort(int*& arr, int len) 

Para armazenar uma amostra da matriz (nossos altos e baixos) e outros elementos, alocamos memória

 int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       int* restElements = new int[len]; //  ,      int restLen = 0; //      

Como você pode ver, alocamos 2 vezes mais memória para armazenar a amostra do que nossa matriz original. Isso é feito caso tenhamos uma matriz classificada e cada próximo elemento será um novo máximo. Somente a segunda parte da matriz de amostra será ocupada. Ou vice-versa (se classificado em ordem decrescente).

Para provar, primeiro você precisa do mínimo inicial e máximo. Basta selecionar o primeiro e o segundo elementos

 if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; 

Amostragem em si

 for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i]) //     { selection[right++] = arr[i]; continue; } if (selection[left + 1] >= arr[i]) //     { selection[left--] = arr[i]; continue; } restElements[restLen++] = arr[i]; //      ,    } 

Agora, temos um conjunto classificado de elementos e os elementos "restantes" que ainda precisamos classificar. Mas primeiro você precisa fazer alguma manipulação de memória.

Libere memória não utilizada

 int selectionLen = right - left - 1; //   int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //       delete[] selection; //   2 * len ,         ,     selection = copy; //  ,    selection     delete[] arr; //    ,         ,       

Faça uma chamada de classificação recursiva para os elementos restantes e mescle-os com a seleção

 FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); 

 void FirstNewGeneratingSort(int*& arr, int len) { if (len < 2) return; int* selection = new int[len << 1]; int left = len - 1; int right = len; int* restElements = new int[len]; int restLen = 0; if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i]) //     { selection[right++] = arr[i]; continue; } if (selection[left + 1] >= arr[i]) //     { selection[left--] = arr[i]; continue; } restElements[restLen++] = arr[i]; //      ,    } int selectionLen = right - left - 1; //   int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //       delete[] selection; //   2 * len ,          ,     selection = copy; //  ,    selection     delete[] arr; //    ,         ,       FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); } 

Vamos verificar a velocidade do algoritmo em comparação com a classificação rápida

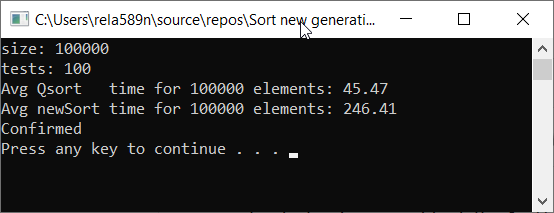
Como você pode ver, isso não é o que queríamos. Quase 6 vezes mais que o QuickSort! Mas, vezes, nesse contexto, é inapropriado usar, pois aqui é o assintótico que importa. Nesta implementação do algoritmo, no pior dos casos, o primeiro e o segundo elementos serão mínimos e máximos. E o restante será copiado para uma matriz separada.

Complexidade do algoritmo:

• Pior caso: O (n ² )
• Caso médio: O (n ² )
• Melhor caso: O (n)

Hmm, isso não é melhor do que a mesma classificação por inserções. Sim, de fato, podemos encontrar o elemento máximo (mínimo) muito rapidamente, e o restante simplesmente não se enquadra na seleção.

Podemos tentar otimizar a classificação de mesclagem. Primeiro, verifique a velocidade do tipo de mesclagem usual:

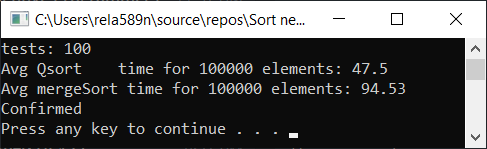
 void newGenerationMergeSort(int* a, int lo, int hi, int& minPortion) { if (hi <= lo) return; int mid = lo + (hi - lo) / 2; if (hi - lo <= minPortion) { //       ,     int* part = glue(a + lo, hi - lo + 1, nullptr, 0); //    FirstNewGeneratingSort(part, hi - lo + 1); for (int i = lo; i <= hi; ++i) { a[i] = part[i - lo]; } delete[] part; return; } newGenerationMergeSort(a, lo, mid, minPortion); newGenerationMergeSort(a, mid + 1, hi, minPortion); int* b = glue(a + lo, mid - lo + 1, a + mid + 1, hi - mid); for (int i = lo; i <= hi; i++) a[i] = b[i - lo]; delete[] b; } 

É necessário algum tipo de invólucro para facilitar o uso.

 void newMergeSort(int *arr, int length) { int portion = log2(length); //      portion *= portion; newGenerationMergeSort(arr, 0, length - 1, portion); } 

Resultado do teste:

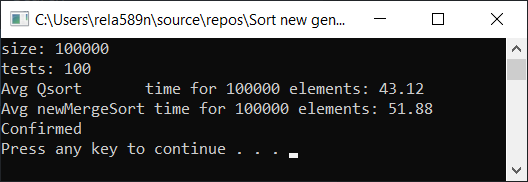
Sim, é observado um aumento na velocidade, mas, no entanto, essa função não funciona tão rápido quanto a Classificação rápida. Além disso, não podemos falar sobre O (n) em matrizes ordenadas. Portanto, esta opção também é descartada.

Opções de otimização para a primeira opção

1. Para garantir que a complexidade não seja O (n ² ), podemos adicionar elementos que não caíram na amostra e não em 1 matriz como antes, mas expandi-los em 2 matrizes. Depois disso, resta apenas classificar essas duas partes e fundi-las com a nossa amostra. Como resultado, obtemos complexidade igual a O (n log n)

2. Como já observamos, o elemento absolutamente máximo (mínimo) na matriz classificada pode ser encontrado rapidamente, e isso não é muito eficaz. É aqui que a classificação por inserção entra para nos ajudar. A cada iteração da seleção, verificaremos se podemos inserir o elemento de fluxo em um conjunto dos últimos, por exemplo, oito inseridos.

Se não estiver claro agora, não fique chateado. Deveria ser assim. Agora tudo ficará claro no código e as perguntas desaparecerão.

A versão correta residual do algoritmo:

A assinatura é a mesma da versão anterior

 void newGenerationSort(int*& arr, int len) 

Mas deve-se notar que esta opção assume um ponteiro para o primeiro parâmetro no qual a operação delete [] pode ser chamada (por que - veremos mais adiante). Ou seja, quando alocamos memória, atribuímos o endereço do início da matriz para esse ponteiro.

Preparação preliminar

Neste exemplo, o chamado "coeficiente de recuperação" é apenas uma constante com um valor de 8. Ele mostra quantos elementos máximos tentamos passar para inserir um novo "abaixo do máximo" ou "abaixo do mínimo" em seu lugar.

 int localCatchUp = min(catchUp, len); //            insertionSort(arr, 0, localCatchUp - 1); //     localCatchUp  if (len <= localCatchUp) //       n <= catchUp ,   return; //    (      ) 

Para armazenar a amostra, crie uma matriz

Se algo não estiver claro, veja a explicação na versão inicial

 int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       

Preencha os primeiros elementos da matriz de seleção

 selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; } 

Deixe-me lembrá-lo de que novos mínimos vão para o lado esquerdo do centro da matriz de amostras e novos máximos vão para o lado direito

Crie matrizes para armazenar itens não selecionados

 int restLen = len >> 1; //     len / 2 int* restFirst = new int[restLen]; int* restSecond = new int[restLen]; int restFirstLen = 0; int restSecondLen = 0; 

Agora, o mais importante é a seleção correta de elementos da matriz de origem

O ciclo começa com localCatchUp (porque os elementos anteriores já inseriram nossa amostra como os valores a partir dos quais iniciaremos). E vai até o fim. Então, depois, no final, todos os elementos serão distribuídos na matriz de seleção ou em uma das matrizes de sub-seleção.

Para verificar se podemos inserir um elemento na seleção, basta verificar se é mais (ou igual) às 8 posições do elemento à esquerda (direita - localCatchUp). Se for esse o caso, basta inseri-lo na posição desejada com uma passagem por esses elementos. Isso foi para o lado direito, ou seja, para o máximo de elementos. Da mesma forma, fazemos o inverso para os mínimos. Se você não conseguir inseri-lo em nenhum dos lados da seleção, jogaremos em uma das outras matrizes.

O loop será mais ou menos assim:

 for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] > selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) { // i -  restFirst[restFirstLen++] = arr[i]; } else { restSecond[restSecondLen++] = arr[i]; } } 

Novamente, o que está acontecendo aqui? Primeiro, tentamos empurrar o elemento para os altos. Não está funcionando - Se possível, jogue-o nos pontos baixos. Se for impossível fazer isso também - coloque-o em restFirst ou restSecond.

A parte mais difícil acabou. Agora, após o loop, temos uma matriz classificada com uma seleção (elementos iniciam no índice [left + 1] e terminam em [right - 1] ), bem como as matrizes restFirst e restSecond de comprimento restFirstLen e restSecondLen, respectivamente.

Como no exemplo anterior, antes da chamada recursiva, liberamos a memória da matriz principal (já salvamos todos os seus elementos)

 delete[] arr; 

Nossa matriz de seleção pode conter muitas células de memória não utilizada. Antes de uma chamada recursiva, você precisa liberá-la.

Libere memória não utilizada

 int selectionLen = right - left - 1; //     int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //        delete[] selection; //    2 * len   selection = copy; //      ,   

Agora execute nossa função de classificação recursivamente para as matrizes restFirst e restSecond

Para entender como ele funciona, primeiro você precisa olhar o código até o fim. Por enquanto, você só precisa acreditar que, após chamadas recursivas, as matrizes restFirst e restSecond serão classificadas.

 newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); 

E, finalmente, precisamos mesclar 3 matrizes no resultante e atribuí-lo ao ponteiro arr.

Você pode primeiro mesclar restFirst + restSecond em alguma matriz restFull e, em seguida, mesclar seleção + restFull . Mas esse algoritmo possui uma propriedade que provavelmente a matriz de seleção conterá muito menos elementos do que qualquer outra matriz. Suponha que a seleção contenha 100 elementos, restFirst contenha 990 e restSecond contenha 1010. Em seguida, para criar uma matriz restFull , é necessário executar 990 + 1010 = 2000 operações de cópia. Em seguida, para mesclar com a seleção - outras 2000 + 100 cópias. Total com essa abordagem, a cópia total será 2000 + 2100 = 4100.

Vamos aplicar a otimização aqui. Primeira mesclagem de seleção e restFirst na matriz de seleção . Operações de cópia: 100 + 990 = 1090. Em seguida, mescle a seleção e as matrizes restSecond e gaste outras 1090 + 1010 = 2100 cópias. No total, serão lançados 2100 + 1090 = 3190, quase um quarto a menos do que na abordagem anterior.

A mesclagem final de matrizes

 int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst selectionLen += restFirstLen; part2 = restSecond; part2Len = restSecondLen; } else { glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond part2Len = restFirstLen + restSecondLen; } glueDelete(arr, selection, selectionLen, part2, part2Len); 

Como você pode ver, se é mais lucrativo mesclar a seleção com o restFirst , o fazemos. Caso contrário, mesclamos como em "restFull"

 /// works only if arr is pointer assigned by new keyword void newGenerationSort(int*& arr, int len) { int localCatchUp = min(catchUp, len); //            insertionSort(arr, 0, localCatchUp - 1); //     localCatchUp  if (len <= localCatchUp) //       n <= catchUp  return; //      int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; } int restLen = len >> 1; int* restFirst = new int[restLen]; int* restSecond = new int[restLen]; int restFirstLen = 0; int restSecondLen = 0; for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] >= selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) { // i -  restFirst[restFirstLen++] = arr[i]; } else { restSecond[restSecondLen++] = arr[i]; } } delete[] arr; int selectionLen = right - left - 1; //     int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //        delete[] selection; //    2 * len   selection = copy; //      ,   newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst selectionLen += restFirstLen; part2 = restSecond; part2Len = restSecondLen; } else { glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond part2Len = restFirstLen + restSecondLen; } glueDelete(arr, selection, selectionLen, part2, part2Len); } 

Agora tempo de teste

 #include <iostream> #include <ctime> #include <vector> #include <algorithm> #include "time_utilities.h" #include "sort_utilities.h" using namespace std; using namespace rela589n; void printArr(int* arr, int len) { for (int i = 0; i < len; ++i) { cout << arr[i] << " "; } cout << endl; } bool arraysEqual(int* arr1, int* arr2, int len) { for (int i = 0; i < len; ++i) { if (arr1[i] != arr2[i]) { return false; } } return true; } int* createArray(int length) { int* a1 = new int[length]; for (int i = 0; i < length; i++) { a1[i] = rand(); //a1[i] = (i + 1) % (length / 4); } return a1; } int* array_copy(int* arr, int length) { int* a2 = new int[length]; for (int i = 0; i < length; i++) { a2[i] = arr[i]; } return a2; } void tester(int tests, int length) { double t1, t2; int** arrays1 = new int* [tests]; int** arrays2 = new int* [tests]; for (int t = 0; t < tests; ++t) { //    int* arr1 = createArray(length); arrays1[t] = arr1; arrays2[t] = array_copy(arr1, length); } t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { quickSort(arrays1[t], 0, length - 1); } t2 = getCPUTime(); cout << "Avg Qsort time for " << length << " elements: " << (t2 - t1) * 1000 / tests << endl; int portion = catchUp = 8; t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { newGenerationSort(arrays2[t], length); } t2 = getCPUTime(); cout << "Avg newGenSort time for " << length << " elements: " << (t2 - t1) * 1000 / tests //<< " Catch up coef: "<< portion << endl; bool confirmed = true; //     for (int t = 0; t < tests; ++t) { if (!arraysEqual(arrays1[t], arrays2[t], length)) { confirmed = false; break; } } if (confirmed) { cout << "Confirmed" << endl; } else { cout << "Review your code! Something wrong..." << endl; } } int main() { srand(time(NULL)); int length; double t1, t2; cout << "size: "; cin >> length; int t; cout << "tests: "; cin >> t; tester(t, length); system("pause"); return 0; } 

 // [min, max] int random(int min, int max) { return min + rand() % ((max + 1) - min); } void quickSort(int * arr, int b, int e) { int l = b, r = e; int piv = arr[random(l, r)]; while (l <= r) { for (; arr[l] < piv; ++l); for (; arr[r] > piv; --r); if (l <= r) swap(arr[l++], arr[r--]); } if (b < r) quickSort(arr, b, r); if (e > l) quickSort(arr, l, e); } 

 #pragma once #if defined(_WIN32) #include <Windows.h> #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) #include <unistd.h> #include <sys/resource.h> #include <sys/times.h> #include <time.h> #else #error "Unable to define getCPUTime( ) for an unknown OS." #endif /** * Returns the amount of CPU time used by the current process, * in seconds, or -1.0 if an error occurred. */ double getCPUTime() { #if defined(_WIN32) /* Windows -------------------------------------------------- */ FILETIME createTime; FILETIME exitTime; FILETIME kernelTime; FILETIME userTime; if (GetProcessTimes(GetCurrentProcess(), &create;Time, &exit;Time, &kernel;Time, &user;Time) != -1) { SYSTEMTIME userSystemTime; if (FileTimeToSystemTime(&user;Time, &user;SystemTime) != -1) return (double)userSystemTime.wHour * 3600.0 + (double)userSystemTime.wMinute * 60.0 + (double)userSystemTime.wSecond + (double)userSystemTime.wMilliseconds / 1000.0; } #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) /* AIX, BSD, Cygwin, HP-UX, Linux, OSX, and Solaris --------- */ #if defined(_POSIX_TIMERS) && (_POSIX_TIMERS > 0) /* Prefer high-res POSIX timers, when available. */ { clockid_t id; struct timespec ts; #if _POSIX_CPUTIME > 0 /* Clock ids vary by OS. Query the id, if possible. */ if (clock_getcpuclockid(0, &id;) == -1) #endif #if defined(CLOCK_PROCESS_CPUTIME_ID) /* Use known clock id for AIX, Linux, or Solaris. */ id = CLOCK_PROCESS_CPUTIME_ID; #elif defined(CLOCK_VIRTUAL) /* Use known clock id for BSD or HP-UX. */ id = CLOCK_VIRTUAL; #else id = (clockid_t)-1; #endif if (id != (clockid_t)-1 && clock_gettime(id, &ts;) != -1) return (double)ts.tv_sec + (double)ts.tv_nsec / 1000000000.0; } #endif #if defined(RUSAGE_SELF) { struct rusage rusage; if (getrusage(RUSAGE_SELF, &rusage;) != -1) return (double)rusage.ru_utime.tv_sec + (double)rusage.ru_utime.tv_usec / 1000000.0; } #endif #if defined(_SC_CLK_TCK) { const double ticks = (double)sysconf(_SC_CLK_TCK); struct tms tms; if (times(&tms;) != (clock_t)-1) return (double)tms.tms_utime / ticks; } #endif #if defined(CLOCKS_PER_SEC) { clock_t cl = clock(); if (cl != (clock_t)-1) return (double)cl / (double)CLOCKS_PER_SEC; } #endif #endif return -1; /* Failed. */ } 

Todos os testes foram realizados na máquina em um percentual. Intel core i3 7100u e 8 GB de RAM

Matriz completamente aleatória

 a1[i] = rand(); 

Matriz parcialmente encomendada

 a1[i] = (i + 1) % (length / 4); 

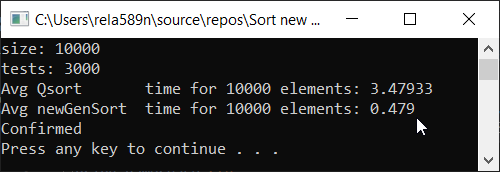
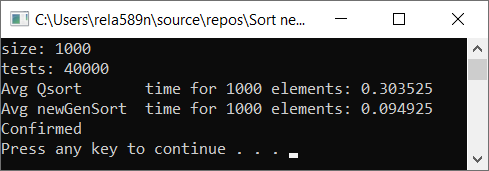
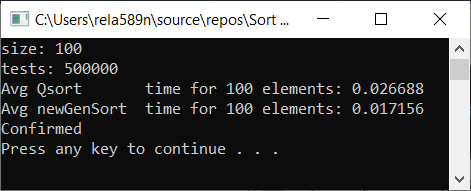
Matriz totalmente classificada

 a1[i] = (i + 1); 

Conclusões

Como você pode ver, o algoritmo funciona e funciona bem. Pelo menos tudo o que queríamos foi alcançado. À custa da estabilidade, não tenho certeza se não verifiquei. Você pode verificar você mesmo. Mas, em teoria, isso deve ser alcançado com muita facilidade. Apenas em alguns lugares, em vez do sinal>, coloque ≥ ou algo assim.