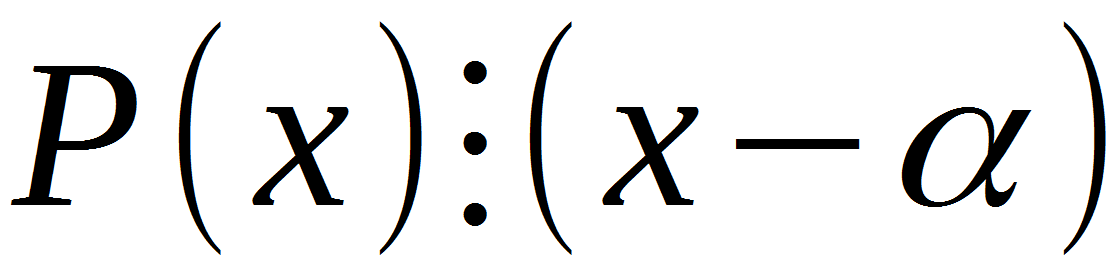
Como regra, em física, ciência da computação e economia, somos confrontados com as equações racionais lineares ou fracionais mais simples, com menos frequência com as quadráticas. E as equações do terceiro e quarto grau? Se você estiver interessado, peço um gato.
Primeiro, considere o conceito de uma equação do mais alto grau. Uma equação do mais alto grau é uma equação da forma:

Neste artigo, considerarei:
1. Equações cúbicas.
2. Cúbico retornável.
3. Aplicação do esquema de Horner e do teorema de Bezout.
4. Equações biquadráticas retornáveis.
Equações cúbicas
Equações cúbicas são aquelas nas quais o grau desconhecido é desconhecido para o termo mais antigo, e têm a seguinte forma:

Tais equações podem ser resolvidas de diferentes maneiras; no entanto, usaremos o conhecimento da escola básica e resolveremos a equação cúbica pelo método de agrupamento:

Neste exemplo, o método de agrupamento é usado, agrupamos os dois primeiros e os últimos dois membros, obtendo colchetes iguais, novamente entendemos, obtendo a equação de dois colchetes.
O produto é igual a zero então, e somente se pelo menos um dos fatores for igual a zero, com base nisso, igualamos cada fator (colchete) a zero, obtendo uma equação quadrática e linear incompleta.
Também é importante notar que o número máximo de raízes de uma equação igual ao grau desconhecido com o termo principal, portanto, em uma equação cúbica, não pode haver mais que três raízes, em um biquadrático (4º grau) não mais que quatro raízes e. etc.
Retornar equações cúbicas
As equações cúbicas de retorno têm a forma:

Eles são chamados retornáveis porque os coeficientes serão espelhados. Equações semelhantes também são resolvidas pelos métodos escolares, mas um pouco mais complicadas:

Primeiro, o agrupamento é realizado e, usando as fórmulas de multiplicação abreviada, decompomos os fatores resultantes. Mais uma vez, temos 2 parênteses iguais, "nós os retiramos". Obtemos dois fatores (colchetes) e os resolvemos como duas equações diferentes.
Teorema de Bezout e esquema de Horner
O teorema de Bezout foi descoberto, surpreendentemente, por Etienne Bezout, um matemático francês que se preocupava principalmente com a álgebra. O teorema de Bezout pode ser formulado da seguinte forma:

Vamos descobrir. P (x) é qualquer polinômio em x, (x - a) é o binômio em que a é uma das raízes inteiras da equação que encontramos entre os divisores do termo livre.
Três pontos, este é um operador indicando que uma expressão é dividida por outra. Daqui resulta que, tendo encontrado pelo menos uma raiz de uma dada equação, podemos aplicar esse teorema a ela. Mas por que esse teorema é necessário, qual é o seu efeito? O teorema de Bezout é uma ferramenta universal se você deseja diminuir o grau de um polinômio. Por exemplo, com sua ajuda, a equação cúbica pode ser transformada em um quadrado, biquadrático, cúbico etc.
Mas uma coisa é entender, mas como dividir? Obviamente, você pode dividi-lo em uma coluna, mas esse método não está disponível para todos, e a probabilidade de cometer um erro é muito alta. Portanto, existe outra maneira, esse é o esquema de Horner. Vou explicar o trabalho dela com um exemplo. Suponha:

E assim, recebemos um polinômio e podemos ter encontrado uma das raízes com antecedência. Agora, desenhamos uma pequena placa de 6 colunas e 2 linhas, em cada coluna da primeira linha (exceto a primeira), introduzimos os coeficientes da equação. E na primeira coluna da linha 2, adicionamos o valor de a (a raiz encontrada). Então, o primeiro coeficiente, no nosso caso 5, acabamos de explodir. Os valores das seguintes colunas são calculados da seguinte maneira:

(A imagem é emprestada
aqui )
Em seguida, fazemos o mesmo com o restante das colunas. O valor da última coluna (2 linhas) será o restante da divisão, no nosso caso 0, se você receber um número diferente de 0, precisará escolher uma abordagem diferente. Um exemplo para uma equação cúbica:

Equações biquadráticas retornáveis
Também consideramos as equações cúbicas de retorno acima e agora analisamos as equações biquadráticas. Sua visão geral:

Ao contrário da equação de retorno cúbico, nem todo mundo tem um par biquadrático em relação aos coeficientes, mas, caso contrário, são muito semelhantes. Aqui está o algoritmo para resolver essas equações:

Como você pode ver, resolver essas equações não é nada simples. Mas eu vou entender esse caso de qualquer maneira. A solução começa dividindo a equação inteira por x ^ 2. Em seguida, agrupamos, aqui introduzi especificamente uma linha adicional para maior clareza. Depois disso, fazemos o truque e inserimos o primeiro colchete 2, que primeiro adicionamos e depois subtraímos, a quantidade não será alterada, mas agora podemos dobrar esse colchete no quadrado da soma.
Removemos -2 do colchete, multiplicando-o primeiro por a, após o qual introduzimos uma nova variável t e obtemos a equação quadrática.
Agora vamos passar para um exemplo:

A parte principal, como no algoritmo generalizado, é dividida por x ^ 2, agrupada, colapsada em um quadrado completo, realizamos a substituição de variáveis e resolvemos a equação quadrática. Depois disso, substituímos as raízes obtidas de volta e resolvemos mais 2 equações quadráticas (multiplicadas por x).
Campo de aplicação
Devido ao seu volume e especificidade, equações de graus mais altos raramente encontram sua aplicação. No entanto, ainda existem exemplos, a equação de Poisson para processos adiabáticos em Física.
Conclusão
Neste artigo, considerei apenas equações cúbicas e biquadráticas. No entanto, o teorema de Bezout considerado (e o esquema de Horner) pode ser usado para resolver equações de 5, 6, 7 e outros graus, mesmo que sua aplicação seja limitada.