Modelagem GPR

Georadar (um dispositivo técnico de rádio para som de subsuperfície, GPR, Radar de penetração no solo), que atualmente é amplamente utilizado - desde o mapeamento de buracos de coelho e estudo de lagartos até buscas em minas , continua sendo um prazer bastante caro.


Tela GPR (quadro do programa de TV britânico "Command of the Time")

Mas é possível avaliar suas capacidades e estudar vários aspectos da interação do campo eletromagnético do georadar com o meio ambiente sem adquirir / alugar um dispositivo de "ferro". O pacote gprMax ( gpr - da abreviatura GPR, Max - as letras iniciais do nome de James Clerk Maxwell, que lançou as bases da eletrodinâmica), distribuído sob a licença GNU GPL v3, nos ajudará nisso.
Os autores deste projeto, lançado em 1996, são Craig Warren, da Universidade da Nortúmbria e Antonis Giannopoulos, da Universidade de Edimburgo. O pacote foi originalmente desenvolvido em C e, em seguida, completamente reescrito nas combinações Python 3 / Cython.


A instalação do pacote requer compiladores instalados que suportam OpenMP (Ferramentas de compilação do Microsoft Visual C ++ 2015 (esta versão é recomendada!) Para Windows / gcc para Linux), a biblioteca NumPy e o compilador Cython. Após fazer o download do repositório no GitHub e descompactar o código-fonte do projeto, vá para a pasta raiz e execute os comandos:

python setup.py build python setup.py install 

Como um “início rápido”, consideramos trabalhar com o pacote usando um exemplo bidimensional simples - a antena transmissora T de um radar pulsado (GPR de impulso) emite um pulso eletromagnético, parte da energia que atinge diretamente a antena receptora R na forma de uma onda direta (DW - onda direta), e algumas penetra através da areia, é refletido a partir da superfície do cilindro condutor e atinge a antena receptora na forma de uma onda refletida (RW - onda refletida):


Formato de arquivo de entrada
Crie a pasta models na pasta raiz do projeto, na qual colocamos o arquivo de texto hello.in contendo os comandos para executar a simulação (os seguintes comandos correspondem à (terceira) versão atual do projeto).

Cada equipe tem a forma:

 #: _1 _2 _3 ... 

Somente um comando pode ser gravado em uma linha e o primeiro caractere da linha que contém o comando deve ser #.

Os comandos podem ser acompanhados de comentários:

 ## 

A ordem dos comandos é importante para os comandos de construção de objetos - esses comandos são executados na ordem em que aparecem no arquivo de entrada.

Forma de pulso

Um pulso eletromagnético emitido por um georadar dura algumas frações de nanossegundo; além disso, três formas de pulso são mais frequentemente usadas:

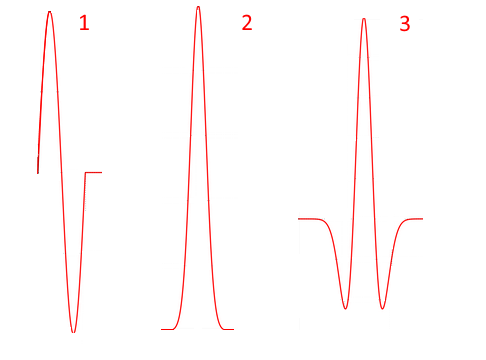
1. um período de onda senoidal (seno)
2. Momento gaussiano (gaussiano)
3. O chapéu mexicano (ricker) é proporcional à segunda derivada da função gaussiana, a forma de curva desse impulso se assemelha a um sombrero (essa forma de impulso foi usada pelo geofísico americano Norman Ricker em 1953 para estudar sinais sísmicos)
   

Para o nosso exemplo, selecionamos um pulso gaussiano (tipo de pulso - gaussiano) com uma frequência central $$$f_c = 1 \\ GHz = 1 \ cdot 10 ^ 9 Hz$ definido pelo comando:

 #waveform: gaussian 1 1e9 pulse 

(1 - amplitude de pulso condicional, etiqueta de pulso - pulso)

Nesse caso, o momento usado na simulação é descrito pela expressão:

$$

$$W (t) = e ^ {- 2 \ cdot {\ pi} ^ 2 \ cdot {f_c} ^ 2 {(t- {1 \ over {f_c}}) ^ 2}$$

Modelo de ambiente e sistema de coordenadas

Na modelagem 2D, a área estudada é dividida em células de um determinado tamanho e o sistema de coordenadas do modelo se parece com isso - os eixos X e Y formam o plano calculado (com uma largura $$$w$ e alto $$$h$ ), o comprimento do modelo ao longo do eixo Z tem um valor igual ao passo de amostragem $$$\ Delta$ .


Ao escolher uma etapa de amostragem, você pode seguir a regra geral - o tamanho da etapa não deve exceder um décimo do menor comprimento de onda estudado no modelo ("10 células por comprimento de onda"):

$$

$$\ Delta \ le 0,1 \ cdot {\ lambda} _ {min}$$

Para determinar o comprimento de onda, é necessário conhecer a frequência máxima levada em consideração no espectro do sinal emitido e a velocidade da onda no meio em consideração.

A velocidade de propagação de uma onda eletromagnética em um meio com constante dielétrica relativa $$${\ epsilon} _r$ , expresso em centímetros por nanossegundo - a unidade de velocidade adotada no radar é determinada pela expressão:

$$

$$v = {30 \ over {\ sqrt {{\ epsilon} _r}}}$$

O comprimento de onda em centímetros é determinado pela expressão:

$$

$$\ lambda = {v \ over f}$$

( $$$f$ - frequência em GHz).
Para exibir a forma do pulso gaussiano e seu espectro, você pode usar o comando:

 python -m tools.plot_source_wave gaussian 1 1e9 5e-9 1e-12 -fft 

(gaussiano - tipo de pulso, 1 - amplitude de pulso, 1e9 - frequência central (1 GHz), 5e-9 - duração de exibição de pulso (5 ns), 1e-12 - intervalo de tempo (1 ps))


De acordo com o espectro de um pulso gaussiano com $$$f_s = 1 \ GHz$ determinar que a -40 dB a frequência $$$f \ aproximadamente 3 \ GHz$ .
Neste exemplo, o meio em que o objeto sondado está localizado, selecionamos areia seca com uma permissividade relativa $$${\ epsilon} _r = 3$ .
Encontre a velocidade de propagação da onda eletromagnética na areia:

$$

$$v = {30 \ over {\ sqrt {3}}} = 17,3 \ cm / ns$$

Defina o comprimento de onda na areia:

$$

$$\ lambda = {v \ over f} = {17,3 \ over {3}} = 5,8 cm = 58 mm$$

Com base nisso, selecionamos a etapa igual para todos os eixos ( $$$\ Delta = {\ Delta} _x = {\ Delta} _y = {\ Delta} _z$ ) e igual a 2 mm = 0,002 m por razões de conveniência (um número inteiro de etapas cabe em 1 cm):

 #dx_dy_dz: 0.002 0.002 0.002 

Limitar a área simulada a um retângulo de largura $$$w$ igual a 80 cm = 0,8 me altura $$$h$ igual a 60 cm = 0,6 m:

 #domain: 0.60 0.60 0.002 

(para um modelo bidimensional, é necessário indicar uma espessura igual a uma etapa (0,002))

O tamanho da área de simulação e o tamanho da etapa espacial determinam o número de células do modelo e, consequentemente, os requisitos de memória do computador.

Descrevemos a areia com condutividade específica $$$\ sigma = 0,01 \ \ cm / m$ e constante dielétrica relativa $$${\ epsilon} _r = 3$ comando:

 #material: 3 0.01 1 0 sand 

(1 corresponde à permeabilidade magnética relativa $$${\ mu} _r$ igual à unidade (sem propriedades magnéticas), 0 - sem perda magnética e etiqueta com areia deste material).

Encha a areia com a maior parte da área simulada (de y = 0 a y = 38 cm = 0,38 m):

 #box: 0 0 0 0.80 0.38 0.002 sand 

(0 0 0 - coordenadas do canto inferior esquerdo, 0,80 0,38 0,002 - coordenadas do canto superior direito (0,002 - etapa de amostragem))
O restante é espaço livre (rótulo free_space), quase equivalente em propriedades do ar ( $$${\ epsilon} _r = 1$ , $$${\ mu} _r = 1$ , $$${\ sigma} = 0$ )
Os limites da área de simulação são apresentados como Absorção de Fronteira (ABC).

Como alvo, escolhemos um cilindro de um condutor ideal (radiação eletromagnética refletindo totalmente) com um raio de 6 cm = 0,06 m com um centro localizado em um ponto com coordenadas x = 25 cm = 0,25 me y = 10 cm = 0,1 m:

 #cylinder: 0.250 0.1 0 0.250 0.1 0.002 0.06 pec 

(pec é um material perfeitamente condutor)

Antenas

O GPR simulado é equipado com duas antenas - transmissoras e receptoras.
Em nosso estudo de caso, representamos uma antena transmissora com um dipolo Hertz cujo comprimento é igual à etapa de amostragem (no caso tridimensional, você pode selecionar uma antena de uma extensa biblioteca) deitada na areia (trabalhando em contato com o meio sondado) a uma distância de 5 cm à esquerda do meio da região (x = 35 cm = 0,35 m, y = 38 cm = 0,38 m):

 #hertzian_dipole: z 0.35 0.380 0.0 pulse 

(z é o eixo de polarização dipolar (para o caso bidimensional (modo 2D TMz) apenas z é válido), pulso é o rótulo da forma do pulso irradiado pela antena)

A antena receptora geralmente está localizada a uma pequena distância constante da receptora, que é chamada de base da unidade de antena (essa opção para a posição relativa das antenas é denominada "deslocamento comum"). Como base, selecione uma distância de 10 cm, para que a coordenada horizontal seja 35 + 10 = 45 cm = 0,45 m (5 cm à direita do meio da região):

 #rx: 0.45 0.38 0.0 

Intervalo de simulação

A escolha da janela de tempo para modelagem é determinada para que o sinal refletido no alvo tenha tempo para alcançar a antena receptora.

Determinamos o tempo aproximado exigido pelo sinal no caso em consideração, levando a distância das antenas ao alvo $$$h = 18 \ \ cm$ :
$$$t \ approx {2 \ cdot h \ over {v}} = {2 \ cdot 18 \ over 17,3} = 2,1 \ \ ns$
Dado que o topo do pulso gaussiano do radar com uma frequência central de 1 GHz é deslocado em relação ao início do eixo do tempo em 1 ns, selecionamos uma janela de tempo de 5 nanossegundos:

 #time_window: 5e-9 

Modelagem

Assim, o conteúdo do arquivo de entrada é o seguinte:


Iniciamos o processo de modelagem:

 python -m gprMax models\hello.in 

Para realizar a simulação, é utilizado o método do domínio do tempo com diferenças finitas (FDTD, domínio do tempo com diferenças finitas) (o algoritmo básico do método foi proposto por Kane Yee), após o qual as células nas quais o modelo está dividido são denominadas células Yee . Uma solução numérica é obtida no domínio do tempo, resolvendo as equações de Maxwell para cada célula.

No caso bidimensional (modo 2D TMz), apenas o componente é calculado $$$E_z$ campo elétrico e componentes $$$H_x$ e $$$H_y$ campo magnético.

Se a quantidade de memória disponível for excedida, uma mensagem sobre a falta de memória será emitida para executar a simulação:


Se algum dos objetos estiver fora do escopo da simulação, uma mensagem de erro será exibida:


Para executar a simulação com o modelo descrito, foram necessários apenas cerca de 56 MB de RAM (se você diminuir o passo pela metade - até 1 mm - os requisitos de memória aumentam para 99 MB).

Após a conclusão da simulação, o arquivo hello.out aparece na pasta de modelos , contendo os resultados da simulação no formato HDF5 , especialmente desenvolvido para armazenar dados numéricos.

Pista de construção

Para visualizar os resultados, construímos os traços:

 python -m tools.plot_Ascan models\hello.out 

Cada faixa (A-scan) apresentada na janela que se abre exibe um gráfico de tempo de um dos componentes do campo eletromagnético no local da antena receptora:


Uma onda direta vinda diretamente da antena transmissora (DW) e uma onda refletida no alvo (RW) são visíveis nos caminhos.

O eixo horizontal do tempo está relacionado à profundidade do alvo que reflete o sinal através da velocidade da onda eletromagnética na substância.

Mas o que acontece se você colocar o comando do cilindro na frente do comando da caixa no arquivo de entrada?


O sinal refletido do cilindro desapareceu - a areia absorveu o cilindro (este é um exemplo da importância da ordem em que os objetos são construídos).

Construção de perfil

Mas mais informativo é o radarograma (radargram) - perfil (B-scan), que é uma combinação de muitas trilhas construídas ao mover o georadar em uma determinada direção - esse é o próprio procedimento para mover um carrinho com um radar pela área estudada.

Altere a descrição das antenas movendo-as para o início do eixo horizontal:

 #hertzian_dipole: z 0.10 0.38 0.0 pulse #rx: 0.20 0.38 0.0 

Definimos o passo para mover as antenas igual a 1 cm = 0,01 m:

 #src_steps: 0.01 0 0 #rx_steps: 0.01 0 0 

Assim, o conteúdo do arquivo de entrada é o seguinte:


Execute a simulação no modo em lote:

 python -m gprMax models\hello.in -n 50 

(50 é o número de etapas que o radar se move).

Após o início, a simulação é realizada sequencialmente para 50 posições GPR:


Após o final da simulação, existem 50 arquivos hello1.out ... hello50.out na pasta do modelo.
Combine esses arquivos no arquivo hello_merged.out com o comando:

 python -m tools.outputfiles_merge models/hello 

Crie um perfil:

 python -m tools.plot_Bscan models\hello_merged.out Ez 

(Ez é o componente do campo eletromagnético pelo qual construímos o perfil - o componente diretamente convertido em tensão)


Como você pode ver, a barra horizontal causada pela onda direta é exibida no perfil acima, e a hipérbole característica causada pela onda refletida e mostrando a alteração na distância do alvo ao GPR quando ele se move é exibida abaixo.

A legenda à direita mostra as cores correspondentes e os pontos fortes do campo. $$$E_z$ (mostrado na pista):
vermelho - $$$E_z> 0$
branco - $$$E_z = 0$
azul - $$$E_z <0$
Ao analisar esses perfis, podemos tirar conclusões sobre a profundidade, tamanho e até a forma dos alvos, e as redes neurais também são usadas para isso.


Rotas e perfil na tela GPR (quadro do programa de TV britânico "Command of the Time")

Mas a reflexão ocorre não apenas a partir de objetos condutores, mas também na fronteira de duas camadas com constantes dielétricas diferentes.

Crie uma segunda camada de areia com constante dielétrica na parte inferior do modelo $$${\ epsilon} _r = 9$ :



Como pode ser visto, abaixo do “traço” da onda direta (DW), um segmento linear da onda (RW) refletido a partir da interface das duas camadas de areia apareceu.

Fora do escopo deste exemplo, os recursos do gprMax, como modelagem tridimensional, formas complexas de superfície, modelos detalhados de antenas, são responsáveis ​​pela dispersão das ondas eletromagnéticas ... Além disso, o pacote pode ser usado não apenas para simular a operação do GPR, mas também para estudar a propagação de ondas eletromagnéticas em vários ambientes, e acelere os cálculos usando a tecnologia NVIDIA CUDA , que fornece um aumento de dez vezes na velocidade em comparação com a computação paralela em uma CPU usando OpenMP. Para aumentar a flexibilidade da modelagem, você pode colocar blocos de código em Python no arquivo de entrada.

Alguns exemplos de uso do pacote gprMax:

• avaliação do efeito das propriedades do solo sobre a eficácia do GPR na busca de minas antipessoal
• verificação da possibilidade de usar radar de penetração no solo para determinação não destrutiva da profundidade do plantio de sementes de milho
• melhorar a qualidade da interpretação dos dados de campo GPR no estudo da resistência de estruturas de passagens subterrâneas através da rodovia
• estudo da relação entre a amplitude do sinal refletido e o diâmetro das barras de reforço no concreto
• avaliação da adequação do GPR para a detecção de vazios em troncos de árvores

Links úteis:

Site oficial gprMax
Guia do usuário do GprMax
gprMax no YouTube