Em toda a geografia: navegação e tarefas geodésicas em diferentes idiomas

Saudações, queridos!

"... o verdadeiro local do navio, embora desconhecido, não é acidental, é, mas é desconhecido em que ponto" V. Aleksishin et al., Practical Navigation, 2006. p. 71

"Os pedestres saíram das duas margens da galáxia ..." (C) Sergey Popov (astrofísico)

À luz das novas tendências no estilo Art Nouveau, eu queria escrever sobre como resolver problemas geodésicos em terreno plano. Mas até agora, a afirmação de que a forma da Terra é convenientemente aproximada por um elipsóide não é heresia e sedição, convido todos os interessados ​​a se unir aos modelos mais conservadores.

• distância entre dois pontos geográficos
• determinação de um ponto por distância conhecida e ângulo azimutal
• determinação da posição de um ponto por distâncias medidas até pontos conhecidos (TOA, TOF)
• determinação da posição de um ponto por tempos de chegada de sinal medidos (TDOA)

Tudo isso em C #, Rust e Matlab, na esfera e elipsóides, com imagens, gráficos, código fonte - sob o corte.

E isso, o KDPV relevante:



Para quem tem pressa (eu mesmo), aqui está o repositório no GitHub , onde estão todos os códigos-fonte com testes e exemplos.

O repositório está organizado de maneira muito simples: atualmente a biblioteca é apresentada em três idiomas e cada implementação está em sua própria pasta:

• C #
• Ferrugem
• Matlab

A implementação mais completa em C #: ao contrário dos outros, existem os chamados métodos nele base longa virtual - é quando um objeto cuja posição você precisa determinar está estacionário e há distâncias medidas a partir de pontos diferentes, com uma posição conhecida.

Para ver como tudo funciona, com quais parâmetros ele chama e que retorna, e conduz o reconhecimento na batalha, existem diferentes demos e testes:

• Aplicativo de console de teste em C #
• Teste a biblioteca inteira no Matlab
• Script de demonstração TOA / TDOA com belas imagens no Matlab
• Script no Matlab para comparar a precisão de soluções para problemas geodésicos em uma esfera (equações de Haversine) e em um elipsóide (Vincenty Equations)
• Para implementação no Rust , o código da biblioteca contém testes. E você pode ver como tudo funciona apenas executando o comando "Cargo-test"

Tentei tornar a biblioteca o mais independente e auto-suficiente possível. Para que, se desejar, você pode simplesmente pegar a peça desejada (referindo-se à fonte, é claro), sem arrastar todo o resto.

Quase sempre os ângulos estão em radianos, distâncias em metros, tempo em segundos.

Agora, vamos começar do começo:

Tarefas de inspeção

Existem duas tarefas geodésicas típicas: direta e inversa.

Se, por exemplo, conheço minhas coordenadas atuais (latitude e longitude) e, em seguida, caminhei 1000 quilômetros estritamente para o nordeste, bem ou norte. Quais coordenadas terei agora? - Descobrir quais coordenadas terei é resolver um problema geodésico direto.

Ou seja: Uma tarefa geodésica direta é encontrar as coordenadas de um ponto por uma distância conhecida e um ângulo de direção.

Com o problema inverso, tudo fica completamente claro - por exemplo, determinei minhas coordenadas e depois andei por algum tempo em linha reta e novamente determinei minhas coordenadas. Descobrir quanto fui significa resolver o problema geodésico inverso.

Ou seja: O problema geodésico inverso é encontrar a distância entre dois pontos com coordenadas geográficas conhecidas.

Você pode resolver esses problemas de várias maneiras, dependendo da precisão necessária e do tempo que estiver disposto a gastar nele.

A maneira mais fácil é imaginar que a Terra é plana - isso é uma esfera. Vamos tentar.
Aqui está a fórmula para resolver o problema direto ( fonte ):

$$

$$\ phi_2 = arcsin (sin \ phi_1cos \ delta + cos \ phi_1sin \ delta cos \ theta)$$

$$

$$\ lambda_2 = \ lambda_1 + atan2 (sin \ theta sin \ delta cos \ phi_1, cos \ delta-sin \ phi_1sin \ phi_2)$$

Aqui $$$\ phi_1$, $$$\ lambda_1$- latitude e longitude do ponto de partida, $$$\ theta$- ângulo direcional, medido no sentido horário a partir da direção norte (quando vista de cima), $$$\ delta$- distância angular d / R. d é a distância medida (percorrida) e R é o raio da terra. $$$\ phi_2$, $$$\ lambda_2$- latitude e longitude do ponto desejado (aquele em que chegamos).

Para resolver o problema inverso, existe outra (não menos simples fórmula):

$$

$$a = sin ^ 2 (\ Delta \ phi / 2) + cos \ phi_1 cos \ phi_2 sin ^ 2 (\ Delta \ lambda / 2)$$

$$

$$d = R * atan2 (\ sqrt a, \ sqrt {1-a})$$

Onde $$$\ phi_1$, $$$\ lambda_1$e $$$\ phi_2$, $$$\ lambda_2$- coordenadas dos pontos, raio R - terra.

As fórmulas descritas são chamadas de Equações de Haversine.

• Em uma implementação C #, as funções correspondentes são chamadas HaversineDirect e HaversineInverse e vivem em Algorithms.cs .
• Em uma implementação Rust, essas são as funções haversine_direct e haversine_inverse .
• Finalmente, no Matlab, as funções são armazenadas em arquivos separados e aqui estão as duas funções:
  HaversineDirect e HaversineInverse

Para C #, fornecerei os nomes das funções e um link para o arquivo em que elas estão localizadas. Para Rust - apenas os nomes das funções (já que a biblioteca inteira está em um arquivo) e para o Matlab - um link para o arquivo de script correspondente, porque no Matlab há uma função - um script.

Obviamente, há algum tipo de problema: a Terra não é uma esfera, mas um plano, e isso de alguma forma deve afetar a aplicabilidade dessas fórmulas e / ou a precisão da solução.

E realmente. Mas, para determinar isso, você precisa comparar com alguma coisa.
Em 1975, Thaddeus Vincenty publicou uma solução computacionalmente eficiente de problemas geodésicos diretos e inversos na superfície de um esferóide (mais conhecido como Ellipsoid of the Revolution, camarada! Ellisoid of Rotation), que se tornou quase padrão.

A descrição do dispositivo do método é desenhada em um artigo separado; portanto, eu me limitarei apenas ao envio ao trabalho original de Vincenti e a uma calculadora on - line com uma descrição do algoritmo.

Na biblioteca UCNLNav, a solução de problemas geodésicos diretos e inversos usando fórmulas de Vincenti está nas seguintes funções:

• C #: VincentyDirect e VincentyInverse em Algorithms.cs .
• Ferrugem: vincenty_inverse e vincenty_direct
• Matlab: Nav_vincenty_direct e Nav_vincenty_inverse .

Porque A solução de Vincenti é iterativa, o número máximo de iterações (it_limit) está presente na lista de parâmetros e o número real de iterações está na lista de resultados. Há também um limite que especifica uma condição de parada (epsilon). Na maioria dos casos, não são necessárias mais de 10 iterações, mas para pontos quase antipodais (como os pólos norte e sul) o método converge pouco e podem ser necessárias até 2000 iterações.

A diferença mais importante é que essas fórmulas executam a solução em um esferóide e seus parâmetros devem ser transferidos para funções. Existe uma estrutura simples para isso que a descreve.

Em todas as implementações, um dos elipsóides padrão pode ser obtido em uma linha. (Muitas vezes, o WGS84 [https://en.wikipedia.org/wiki/World_Geodetic_System] é usado e nós o daremos como exemplo):

• Em C #: Algorithms.cs possui um campo estático Algorithms.WGS84Ellipsoid - ele pode ser passado para métodos.
• Na oxidação:

  let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); 

• No Matlab:

   el = Nav_build_standard_ellipsoid('WGS84'); 

O nome dos parâmetros restantes é bastante óbvio e não deve causar ambiguidades.

Para entender o que nos custará usar soluções para uma esfera em vez de uma elipse, existe um script na implementação do Matlab.

No Matlab, é incrivelmente conveniente exibir qualquer coisa sem gestos desnecessários, então eu o escolhi para demonstração.

A lógica do seu script:

1. Nós defendemos um ponto com coordenadas arbitrárias

 sp_lat_rad = degtorad(48.527683); sp_lon_rad = degtorad(44.558815); 

e uma direção arbitrária (eu escolhi o oeste):

 fwd_az_rad = 1.5 * pi + (rand * pi / 4 - pi / 8); 

2. Damos um passo para uma distância cada vez maior. Por que definimos imediatamente o número de etapas e o tamanho da etapa:

 n_samples = 10000; step_m = 1000; % meters distances = (1:n_samples) .* step_m; 

3. Para cada etapa, resolvemos o problema geodésico direto na esfera e no elipsóide, obtendo o ponto desejado:

 [ h_lats_rad(idx), h_lons_rad(idx) ] = Nav_haversine_direct(sp_lat_rad,... sp_lon_rad,... distances(idx),... fwd_az_rad,... el.mjsa_m); [ v_lats_rad(idx), v_lons_rad(idx), v_rev_az_rad, v_its ] = Nav_vincenty_direct(sp_lat_rad,... sp_lon_rad,... fwd_az_rad,... distances(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

4. Para cada etapa, resolvemos problemas geodésicos inversos - calculamos as distâncias entre os resultados obtidos em uma esfera e um elipsóide:

 [ v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(h_lats_rad(idx),... h_lons_rad(idx),... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

5. Verificamos soluções diretas inversas para ambos os métodos:

 [ ip_v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); ip_h_dist(idx) = Nav_haversine_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el.mjsa_m); 

No script, essa sequência é executada primeiro para um passo = 1000 me depois para um passo = 1 metro.

Primeiro, vamos ver como os resultados das decisões diretas diferem em coordenadas (latitude e longitude), para as quais calculamos os vetores "delta", pois tudo está escrito no Matlab em uma linha:

 d_lat_deg = radtodeg(v_lats_rad - h_lats_rad); %    ( ) d_lon_deg = radtodeg(v_lons_rad - h_lons_rad); %    ( ) 

No eixo, as abcissas serão exibidas em uma escala logarítmica, porque nossas distâncias variam de 1 a 10.000 km:

 figure semilogx(distances, d_lat_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Latitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); figure semilogx(distances, d_lon_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Longitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); 

Como resultado, obtemos esses gráficos para latitude:



E para longitude:



Não entendo em graus, sou sempre guiado pelo método de estimativa "a olho":
1 ° de algo é uma média de 100-110 km. E se o erro for superior a um milionésimo ou pelo menos cem milésimo de parte de um grau - isso é uma má notícia.

A seguir, examinamos as distâncias entre o ponto inicial e o ponto obtido em cada etapa, de acordo com as fórmulas para a esfera e o elipsóide. Calculamos a distância usando as fórmulas de Vincenti (como é obviamente mais precisa - o autor promete um erro em milímetros). Gráficos em metros e quilômetros são muito mais tangíveis e familiares:

 figure semilogx(distances, v_dist, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Endpoint difference by Vincenty)'); xlabel('Distance, m'); ylabel('Difference, m'); 

Como resultado, obtemos a seguinte imagem:



Acontece que em faixas de 10.000 km, os métodos divergem em 10 km.

Se agora tudo é repetido por um passo 1000 vezes menor, ou seja, quando todo o alcance ao longo do eixo X não é de 10.000 km, mas apenas 10 km, a imagem é a seguinte:



Ou seja, a uma distância de 10 km, apenas 20 metros sobem e, por 1-2 metros, as fórmulas divergem apenas a distâncias de cerca de 1000 metros.

A conclusão do capitão é óbvia: se a precisão das fórmulas com a solução na esfera é suficiente para o problema, então as usamos - elas são mais simples e rápidas.

Bem, para aqueles para quem a precisão milimétrica não é suficiente, em 2013 foi publicado um trabalho descrevendo a solução de problemas geodésicos com precisão nanométrica (!). Não tenho certeza de que posso chegar imediatamente aonde isso pode ser necessário, exceto para pesquisas geodésicas ao criar detectores de ondas gravitacionais ou algo absolutamente fantástico).

Agora vamos para o mais saboroso:

Resolvendo problemas de navegação

No momento, a biblioteca pode determinar:

• A localização do objeto pela distância aos pontos, com coordenadas conhecidas em 2D e 3D. Isso é o que chamamos de TOA - Hora de chegada (ou mais corretamente, TOF - Hora de voo)
• A localização do objeto pelas diferenças nos horários de chegada em 2D e 3D. Isso é o que chamamos de TDOA (diferença de horário de chegada).

Na realidade, sempre medimos os intervalos ou horários de chegada de um sinal (e, consequentemente, a diferença) com erros, com ruído. Portanto, a solução dos problemas de navegação na grande maioria dos casos é a minimização de erros. Método dos mínimos quadrados e isso é tudo .

O que precisa ser minimizado é chamado de função residual.

Para tarefas TOA, fica assim:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2 )} - r_i] ^ 2$$

Onde $$$\ epsilon (x, y, z)$- o valor da função residual para um determinado ponto com coordenadas $$$(x, y, z)$; N é o número de pontos de controle com coordenadas $$$(x_i, y_i, z_i)$, $$$r_i$- distâncias medidas dos pontos de referência ao objeto posicionado.

E para tarefas TDOA como esta:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1, j = 2, i \ neq j} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2+ (z-z_i) ^ 2)} - \\ \ sqrt {(x-x_j) ^ 2 + (y-y_j) ^ 2 + (z-z_j) ^ 2)} - \ nu (t_ {Ai} -t_ {Aj})] ^ 2$$

Tudo é o mesmo aqui, apenas pares diferentes de pontos de referência e tempos de chegada correspondentes são considerados $$$t_ {Ai}$e $$$t_ {Aj}$e $$$\ nu$- velocidade de propagação do sinal.

E, portanto, essas funções aparecem no código:




Como você pode ver, ambas as funções funcionam com um número variável de pontos ou linhas de controle. Em geral, as tarefas podem ser diferentes e as funções residuais também.

Por exemplo, você pode resolver o problema não apenas de determinar a localização, mas também de determinar a orientação. Nesse caso, a função residual conterá um ou mais ângulos.

Vamos nos aprofundar na estrutura interna da biblioteca

Nesse estágio, a biblioteca trabalha com tarefas 2D e 3D e o solucionador não sabe e não quer saber como é a funcionalidade minimizada. Isso é alcançado da seguinte maneira.

O solucionador tem dois aspectos: solucionadores 2D e 3D baseados no método Nelder-Mead ou, como também é chamado, no método Simplex.

Como esse método não requer o cálculo de derivadas (a chamada minimização livre de derivadas ), idealmente, o usuário da biblioteca pode usar suas próprias funções residuais, se necessário. Além disso, teoricamente, não há limite superior no número de pontos de controle usados ​​na solução do problema.

Em C # e Rust, os solventes 2D e 3D são métodos genéricos:

 public static void NLM2D_Solve<T>(Func<T[], double, double, double, double> eps, T[] baseElements,... //       : fxi[0] = eps(baseElements, xix[0], xiy[0], z); 

Um exemplo de chamada do solucionador:

 public static void TOA_NLM2D_Solve(TOABasePoint[] basePoints, double xPrev, double yPrev, double z, int maxIterations, double precisionThreshold, double simplexSize, out double xBest, out double yBest, out double radialError, out int itCnt) { NLM2D_Solve<TOABasePoint>(Eps_TOA3D, basePoints, xPrev, yPrev, z, maxIterations, precisionThreshold, simplexSize, out xBest, out yBest, out radialError, out itCnt); } 

Na ferrugem ...

 pub fn nlm_2d_solve<T>(eps: Eps3dFunc<T>, base_elements: &Vec<T>... 

Tudo é idêntico, preciso à sintaxe do idioma.

Em Matlabe, com seu voluntarismo inerente, o solucionador não tem idéia do que os elementos básicos são passados ​​para ele - o próprio usuário deve garantir que o link para a função residual e o conjunto de elementos de suporte passados ​​para o solucionador sejam compatíveis:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(eps, base_elements, .... 

E, portanto, a chamada para o solucionador fica assim:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size) [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(@Nav_eps_toa3d, base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size); end 

Existe um script especial do Matlab para demonstrar a solução dos problemas TOA e TDOA.

A demonstração em 2D não foi escolhida por acaso - não sei se consigo descobrir como exibir a função residual tridimensional de maneira simples e informativa =)

Então No início do script, existem parâmetros que podem ser alterados:

 %% parameters n_base_points = 4; %    area_width_m = 1000; %   max_depth_m = 100; %   ( Z) propagation_velocity = 1500;%     -  max_iterations = 2000; %    precision_threshold = 1E-9; %   simplex_size = 1; %      contour_levels = 32; %      range_measurements_error = 0.01; % 0.01 means 1% of corresponding slant range %    -   1% 

A posição do ponto desejado é definida aleatoriamente na área especificada:

 %% actual target location r_ = rand * area_width_m / 2; az_ = rand * 2 * pi; actual_target_x = r_ * cos(az_); actual_target_y = r_ * sin(az_); actual_target_z = rand * max_depth_m; 

Em seguida, coloque aleatoriamente os pontos de controle, calcule a distância do desejado até eles e exiba tudo:

 %% base points figure hold on grid on base_points = zeros(n_base_points, 4); for n = 1:n_base_points r_ = area_width_m / 2 - rand * area_width_m / 4; az_ = (n - 1) * 2 * pi / n_base_points; base_x = r_ * cos(az_); base_y = r_ * sin(az_); base_z = rand * max_depth_m; dist_to_target = Nav_dist_3d(base_x, base_y, base_z, actual_target_x, actual_target_y, actual_target_z); base_points(n, :) = [ base_x base_y base_z dist_to_target ]; end N =1:n_base_points; plot3(actual_target_x, actual_target_y, actual_target_z,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot3(base_points(N, 1), base_points(N, 2), base_points(N, 3),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); for n = 1:n_base_points line([ actual_target_x, base_points(n, 1) ], [ actual_target_y, base_points(n, 2) ], [ actual_target_z, base_points(n, 3) ]); end view(45, 15); legend('target', 'base points'); title('Placement of base stations and the target'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); zlabel('Z coordinate, m'); 

Como resultado, obtemos a seguinte imagem:



Adicione erros aleatórios às medições de distância:

 % adding range measurement errors base_points(N, 4) = base_points(N, 4) + base_points(N, 4) *... (rand * range_measurements_error - range_measurements_error / 2); 

Construímos a função residual para a região selecionada com uma certa dizimação - caso contrário, os cálculos podem levar um tempo perceptível. Escolhi o tamanho da área de 1000 x 1000 metros e considero a função residual em toda a área após 10 metros:

 % error surface tiles tile_size_m = 10; n_tiles = area_width_m / tile_size_m; %% TOA solution error_surface_toa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_toa(t_x, t_y) = Nav_eps_toa3d(base_points,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf_a = [1:n_tiles] * tile_size_m - area_width_m / 2; surf(surf_a, surf_a, error_surface_toa); title('TOA solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Aqui está a função residual:



É claro que fui um pouco astuto - as posições relativas dos pontos de controle e as desejadas são escolhidas para que elas sempre formem uma figura convexa com o ponto desejado dentro. Em grande parte devido a isso, a superfície tem um mínimo, sem problemas.

Um leitor arrogante pode mudar essa ordem das coisas e tentar definir os pontos de ancoragem e o desejado por acidente.

Agora, mostre tudo junto. Isso é difícil de fazer na superfície - valores diferentes ao longo do eixo vertical. Portanto, é conveniente desenhar tudo em uma fatia bidimensional:

 figure hold on contourf(surf_a, surf_a, error_surface_toa, contour_levels); plot(actual_target_x, actual_target_y,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(base_points(N, 1), base_points(N, 2),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); [ x_prev, y_prev ] = Nav_toa_circles_1d_solve(base_points, actual_target_z, pi / 180, 10, 0.1); [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, actual_target_z,... max_iterations, precision_threshold, simplex_size); plot(x_best, y_best,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); title(sprintf('TOA Solution: Residual function. Target location estimated with E_{radial} = %.3f m in %d iterations', rerr, it_cnt)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Residual function value', 'Actual target location', 'Base points', 'Estimated target location'); 

O resultado é algo como isto:



O erro radial é exibido no cabeçalho do gráfico - a raiz do valor final da função residual. O gráfico mostra que a localização real e a calculada estão em boa concordância, mas a escala não permite determinar quão bem.

Portanto, exibimos a localização calculada do ponto desejado e sua localização real separadamente e calculamos a distância entre eles:

 figure hold on grid on dx = actual_target_x - x_best; dy = actual_target_y - y_best; plot(0, 0,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(dx, dy,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); plot(-dx * 2, -dy * 2, '.w'); plot(dx * 2, dy * 2, '.w'); d_delta = Nav_dist_3d(actual_target_x, actual_target_y, actual_target_z, x_best, y_best, actual_target_z); title(sprintf('TOA Solution: Actual vs. Estimated location, distance: %.3f m', d_delta)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Actual target location', 'Estimated target location'); 

Aqui está o que parece:



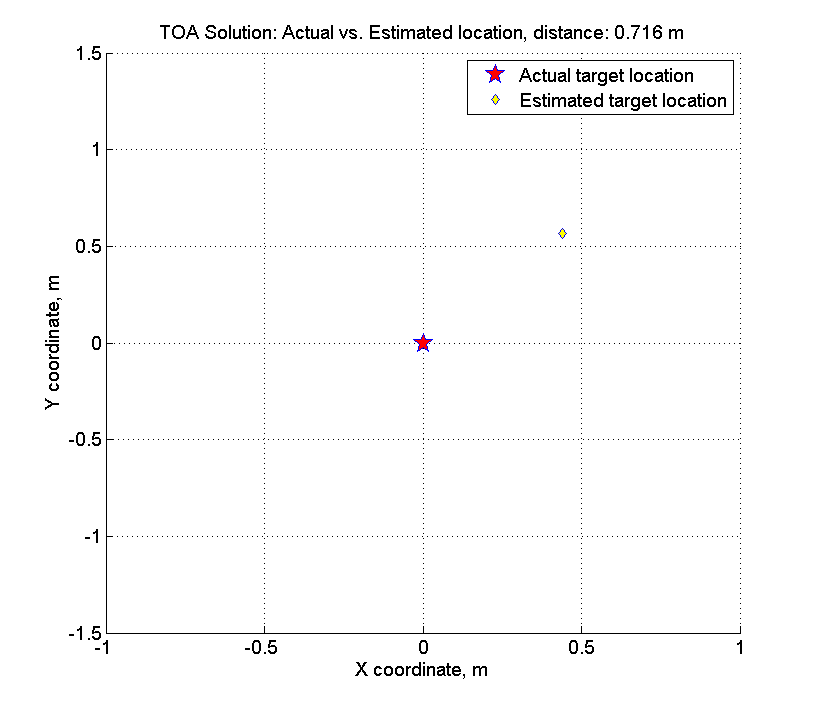
Lembre-se de que temos a amplitude de um erro aleatório - 1% da faixa, em média, a faixa é de ~ 200 a 400 metros, ou seja, a amplitude do erro é de cerca de 2-4 metros. Ao procurar uma solução, cometemos um erro de apenas 70 centímetros.

Agora, por analogia, tentaremos resolver o problema do TDOA com os mesmos dados. Para fazer isso, fingiremos que sabemos apenas os horários de chegada dos sinais do ponto desejado aos pontos de referência (ou vice-versa, isso não importa) - simplesmente dividimos nossas distâncias pela velocidade de propagação do sinal - apenas suas diferenças e não os valores absolutos são importantes.

 % since TDOA works with time difference of arriaval, % we must recalculate base point's distances to times base_points(N,4) = base_points(N,4) / propagation_velocity; base_lines = Nav_build_base_lines(base_points, propagation_velocity); 

Crie e desenhe uma superfície de erros:

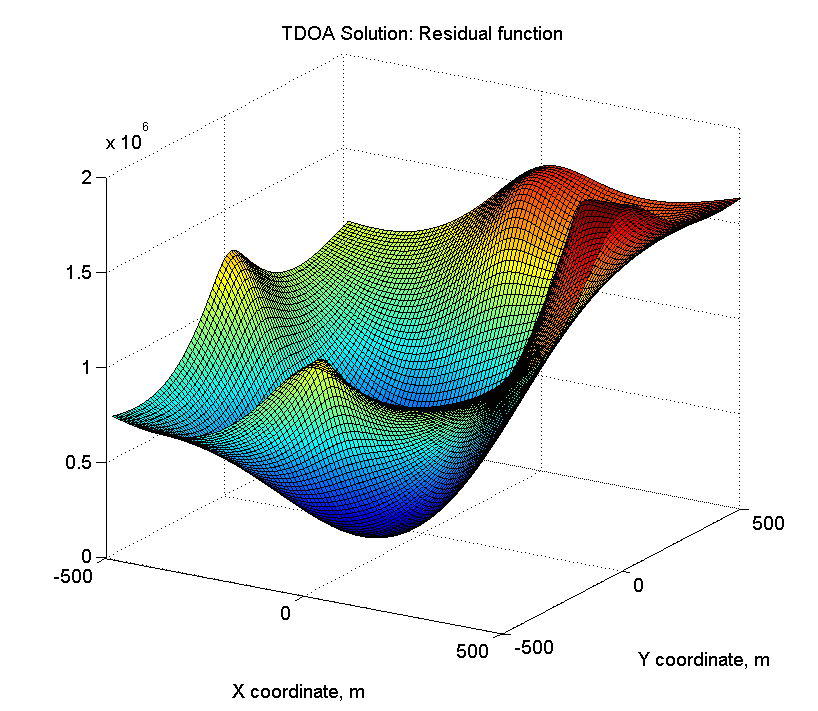
 error_surface_tdoa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_tdoa(t_x, t_y) = Nav_eps_tdoa3d(base_lines,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf(surf_a, surf_a, error_surface_tdoa); title('TDOA Solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Acontece algo como isto:



E a vista de cima com pontos de referência, as posições reais e calculadas do ponto desejado:



E com mais detalhes, a discrepância entre o local real e o calculado:



Nesse caso em particular, a solução TDOA acabou sendo ainda melhor que a solução TOA - o erro absoluto é de 0,3 metros.

Bom no modelo - você sempre sabe exatamente onde o ponto desejado está realmente localizado. É pior no ar - talvez haja vários pontos de vista, debaixo d'água você acabou de calcular algo e isso é tudo - em 99% dos casos, para calcular o desvio da localização real, ele (esse local) também deve ser calculado primeiro.

Agora, como conclusão, combinaremos nosso novo conhecimento sobre tarefas geodésicas e de navegação.

Acorde final

O mais próximo possível da situação na vida real:

• Suponha que nossos pontos de referência tenham receptores GNSS integrados e que apenas conhecemos suas coordenadas geográficas
• a coordenada vertical é desconhecida para nós (Problema 3D)
• medimos apenas os tempos de chegada do sinal a partir dos pontos de referência no desejado ou vice-versa

Essa situação é descrita no teste mais recente nas três implementações. De alguma forma, privou Rust e analisarei o exemplo final.

Portanto, o teste mais recente na biblioteca. Como coordenadas do ponto desejado, escolhi um lugar no parque, onde geralmente ando com o cachorro.

 #[test] fn test_tdoa_locate_3d() { let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); let base_number = 4; // 4   let start_base_z_m: f64 = 1.5; //  Z     let base_z_step_m = 5.0; //        5  let actual_target_lat_deg: f64 = 48.513724 // singed degrees let actual_target_lon_deg: f64 = 44.553248; // signed degrees let actual_target_z_m: f64 = 25.0; // meters - ,    ! // generate base points via Vincenty equations let mut base_points = Vec::new(); let start_dst_projection_m = 500.0; //      500  let dst_inc_step_m = 50.0; //   -  50   // azimuth step let azimuth_step_rad = PI2 / base_number as f64; //     let actual_target_lat_rad = actual_target_lat_deg.to_radians(); let actual_target_lon_rad = actual_target_lon_deg.to_radians(); // signal propagation speed let velocity_mps = 1450.0; // m/s,        //     for base_idx in 0..base_number { //        let dst_projection_m = start_dst_projection_m + dst_inc_step_m * base_idx as f64; //       let azimuth_rad = azimuth_step_rad * base_idx as f64; //        Vincenty let vd_result = vincenty_direct(actual_target_lat_rad, actual_target_lon_rad, azimuth_rad, dst_projection_m, &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); //   Z let base_z_m = start_base_z_m + base_z_step_m * base_idx as f64; //        let dz_m = actual_target_z_m - base_z_m; //      let slant_range_m = (dst_projection_m * dst_projection_m + dz_m * dz_m).sqrt(); //   .          Rust   ! base_points.push((vd_result.0.to_degrees(), vd_result.1.to_degrees(), base_z_m, slant_range_m / velocity_mps)); } //     -   NAN- let lat_prev_deg = f64::NAN; let lon_prev_deg = f64::NAN; let prev_z_m = f64::NAN; //   let tdoa_3d_result = tdoa_locate_3d(&base_points, lat_prev_deg, lon_prev_deg, prev_z_m, NLM_DEF_IT_LIMIT, NLM_DEF_PREC_THRLD, 10.0, &el, velocity_mps); //          let vi_result = vincenty_inverse(actual_target_lat_rad, actual_target_lon_rad, tdoa_3d_result.0.to_radians(), tdoa_3d_result.1.to_radians(), &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); assert!(vi_result.0 < start_dst_projection_m * 0.01, "Estimated location is farer than limit (1%): {}", vi_result.0); assert_approx_eq!(tdoa_3d_result.2, actual_target_z_m, start_dst_projection_m * 0.05); assert!(tdoa_3d_result.3 < start_dst_projection_m * 0.01, "Residual function greater than limit (1%): {}", tdoa_3d_result.3); assert!(tdoa_3d_result.4 < NLM_DEF_IT_LIMIT, "Method did not converge: iterations limit exeeded {}", tdoa_3d_result.4); } 

Como resultado, temos:
Localização real (Lat, Lon, Z): 48.513724 44.553248 25
Posição calculada (Lat, Lon, Z): 48.513726 44.553252 45.6
Distância entre pontos na superfície (m): 0.389
Diferença na coordenada Z (m): 20,6

A correspondência "plano" é muito boa, o erro é de apenas 40 centímetros e a coordenada vertical é de 20 metros. Por que isso está acontecendo, sugiro que os leitores pensem =)

PS

A biblioteca descrita é um projeto puramente educacional, que pretendo desenvolver e reabastecer ainda mais. Os planos incluem implementação em C e elaboração de documentação abrangente.

Sobre isso, deixe-me despedir-se, obrigado por sua atenção.Ficarei infinitamente satisfeito com qualquer feedback.
Espero que o artigo e a biblioteca sejam úteis.
Relatar quaisquer erros (gramaticais e lógicos) - Eu o corrigirei.

PPS

Para o caso, aqui está um link para os intérpretes online do Matlab / Octave (e não apenas):

• Compilador Octave Online
• Octave online
• Oitava GNU