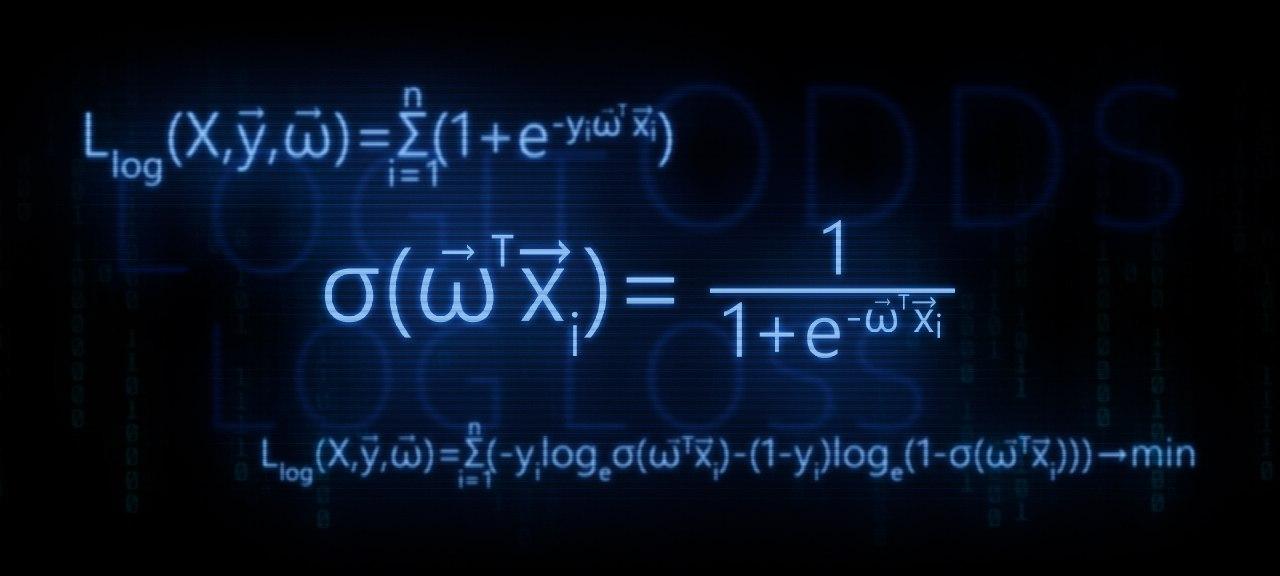
Neste artigo, analisaremos os cálculos teóricos da conversão
da função de regressão linear para a função de transformação inversa de log (em outras palavras, a função de resposta logística) . Em seguida, usando o arsenal do
método de máxima verossimilhança , de acordo com o modelo de regressão logística, derivamos a função de perda
Logistic Loss , ou seja, determinamos a função pela qual os parâmetros do vetor de peso são selecionados no modelo de regressão logística
vecw .
O esboço do artigo:
- Vamos repetir sobre a relação direta entre duas variáveis
- Identificamos a necessidade de converter a função de regressão linear f(w,xi)= vecwT vecxi para a função de resposta logística sigma( vecwT vecxi)= frac11+e− vecwT vecxi
- Realizamos as transformações e derivamos a função de resposta logística
- Vamos tentar entender por que o método dos mínimos quadrados é ruim ao escolher parâmetros vecw Recursos de perda logística
- Utilizamos o método de máxima verossimilhança para determinar a função de seleção de parâmetro vecw :
5.1 Caso 1: Função de perda logística para objetos com designação de classe 0 e 1 :
Llog(X, vecy, vecw)= soma limitesni=1(−yi mkern2muloge mkern5mu sigma( vecwT vecxi)−(1−yi) mkern2muloge mkern5mu(1− sigma( vecwT vecxi))) rightarrowmin
5.2 Caso 2: Função de perda logística para objetos com designações de classe -1 e +1 :
Llog(X, vecy, vecw)= sum limitsni=1 mkern2muloge mkern5mu(1+e−yi vecwT vecxi) rightarrowmin
O artigo está repleto de exemplos simples, nos quais todos os cálculos são fáceis de fazer verbalmente ou em papel; em alguns casos, uma calculadora pode ser necessária. Então prepare-se :)
Este artigo é mais direcionado a especialistas em dados com um nível inicial de conhecimento nos conceitos básicos de aprendizado de máquina.
O artigo também fornecerá código para desenhar gráficos e cálculos. Todo o código é escrito em
python 2.7 . Eu explicarei antecipadamente sobre a "novidade" da versão usada - esta é uma das condições para fazer um curso bem conhecido da
Yandex na plataforma on-line não menos conhecida para educação on-line
Coursera e, como você pode presumir, o material foi preparado com base nesse curso.
01. linha reta
É bastante razoável fazer a pergunta - onde está o relacionamento direto e a regressão logística?
Tudo é simples! A regressão logística é um dos modelos que pertencem ao classificador linear. Em palavras simples, o objetivo de um classificador linear é prever valores-alvo
y de variáveis (regressores)
X . Acredita-se que a relação entre os sinais
X e valores alvo
y linear. Portanto, o nome do classificador em si é linear. Generalizado muito grosso modo, o modelo de regressão logística é baseado no pressuposto de que existe uma relação linear entre as características
X e valores alvo
y . Aqui está - uma conexão.
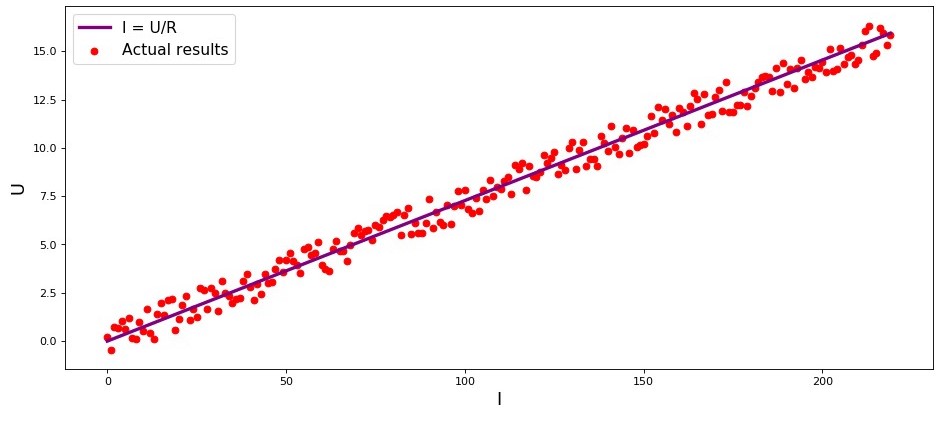
O estúdio é o primeiro exemplo, e com razão, da dependência direta das quantidades estudadas. No processo de preparação do artigo, deparei-me com um exemplo que já estava com
dor de garganta - a dependência da força da corrente em relação à tensão
("Applied Regression Analysis", N. Draper, G. Smith) . Aqui vamos considerar também.
De acordo com
a lei de Ohm:I=U/R onde
I - força atual
U - tensão
R - resistência.
Se não
conhecêssemos a lei de Ohm , poderíamos encontrar a dependência empiricamente mudando
U e medindo
I enquanto apoia
R fixo. Então veríamos que o gráfico de dependência
I de
U dá uma linha mais ou menos reta passando pela origem. Dissemos "mais ou menos", porque, embora a dependência seja realmente precisa, nossas medidas podem conter pequenos erros e, portanto, os pontos no gráfico podem não cair exatamente na linha, mas serão espalhados aleatoriamente em torno dela.
Quadro 1 “Dependência
I de
U "
Código de renderização de gráficoimport matplotlib.pyplot as plt %matplotlib inline import numpy as np import random R = 13.75 x_line = np.arange(0,220,1) y_line = [] for i in x_line: y_line.append(i/R) y_dot = [] for i in y_line: y_dot.append(i+random.uniform(-0.9,0.9)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R') plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results') plt.xlabel('I', size = 16) plt.ylabel('U', size = 16) plt.legend(prop = {'size': 14}) plt.show()
02. A necessidade de transformações da equação de regressão linear
Considere outro exemplo. Imagine que trabalhamos em um banco e somos confrontados com a tarefa de determinar a probabilidade de um empréstimo pagar por um mutuário, dependendo de alguns fatores. Para simplificar a tarefa, consideramos apenas dois fatores: o salário mensal do mutuário e o pagamento mensal pelo reembolso do empréstimo.
O problema é muito condicional, mas com este exemplo podemos entender por que não basta usar
a função de regressão linear para resolvê-lo, e também descobriremos que transformações com a função é necessário realizar.
Voltamos por exemplo. Entende-se que quanto maior o salário, mais o mutuário poderá direcionar mensalmente para reembolsar o empréstimo. Ao mesmo tempo, para uma certa faixa de salários, essa dependência será bastante linear para si mesma. Por exemplo, considere uma faixa salarial de 60.000 a 200.000 e suponha que, na faixa indicada de salários, a dependência do tamanho do pagamento mensal sobre o valor do salário seja linear. Suponhamos que, para a faixa especificada de salários, tenha sido revelado que a relação salário / pagamento não pode cair abaixo de 3 e que o mutuário ainda deve ter 5.000 R em reserva. E somente neste caso, assumiremos que o devedor devolverá o empréstimo ao banco. Então, a equação de regressão linear assume a forma:
f(w,xi)=w0+w1xi1+w2xi2,onde
w0=−5.000 ,
w1=1 ,
w2=−3 ,
xi1 -
salário i mutuário
xi2 -
pagamento de empréstimo i mutuário.
Substituindo pagamento de salário e empréstimo por parâmetros fixos na equação
vecw Você pode decidir se deseja conceder ou recusar um empréstimo.
No futuro, observamos que, para determinados parâmetros
vecw a função de regressão linear usada na
função de resposta logística produzirá grandes valores que dificultam o cálculo das probabilidades de reembolso do empréstimo. Portanto, propõe-se reduzir nossos coeficientes, digamos, 25.000 vezes. A partir dessa conversão em índices, a decisão de conceder um empréstimo não será alterada. Lembremos deste momento para o futuro e, agora, para tornar ainda mais claro o que estamos falando, consideraremos a situação com três possíveis tomadores de empréstimos.
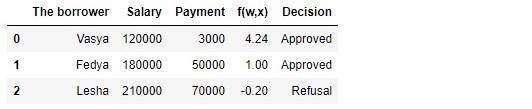
Quadro 1 "Potenciais tomadores de empréstimos"
Código para gerar a tabela import pandas as pd r = 25000.0 w_0 = -5000.0/r w_1 = 1.0/r w_2 = -3.0/r data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']), 'Salary':np.array([120000,180000,210000]), 'Payment':np.array([3000,50000,70000])} df = pd.DataFrame(data) df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2 decision = [] for i in df['f(w,x)']: if i > 0: dec = 'Approved' decision.append(dec) else: dec = 'Refusal' decision.append(dec) df['Decision'] = decision df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]
De acordo com a tabela, Vasya, com um salário de 120.000 R, deseja obter esse empréstimo para pagá-lo em 3.000 R por mês. Determinamos que, para aprovar o empréstimo, o salário de Vasya deveria ser três vezes maior que o pagamento e que ainda havia 5.000R. Vasya satisfaz este requisito:
120.000−3∗3.000−5.000=106.000 . Restam até 106.000P. Apesar do fato de que, ao calcular
f(w,xi) reduzimos as chances
vecw 25.000 vezes, o resultado foi o mesmo - o empréstimo pode ser aprovado. Fedya também receberá um empréstimo, mas Lesha, apesar de receber mais, terá que restringir seu apetite.
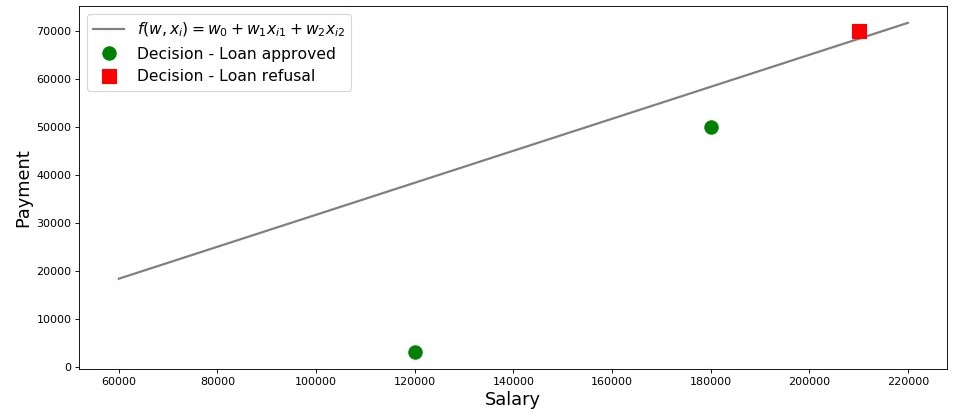
Vamos desenhar um cronograma para este caso.
Quadro 2 “Classificação dos mutuários”
Código para plotagem salary = np.arange(60000,240000,20000) payment = (-w_0-w_1*salary)/w_2 fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$') plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'], 'o', color ='green', markersize = 12, label = 'Decision - Loan approved') plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'], 's', color = 'red', markersize = 12, label = 'Decision - Loan refusal') plt.xlabel('Salary', size = 16) plt.ylabel('Payment', size = 16) plt.legend(prop = {'size': 14}) plt.show()
Então, nossa linha, construída de acordo com a função
f(w,xi)=w0+w1xi1+w2xi2 , separa os tomadores "ruins" dos "bons". Os mutuários cujos desejos não coincidem com as oportunidades estão acima da linha direta (Lesha), aqueles que são capazes de reembolsar o empréstimo de acordo com os parâmetros do nosso modelo estão abaixo da linha direta (Vasya e Fedya). Caso contrário, podemos dizer isso - nossa linha divide os mutuários em duas classes. Nós os denotamos da seguinte forma: para a classe
+1 classifique os mutuários que provavelmente reembolsarão o empréstimo à classe
−1 ou
0 designaremos os devedores que provavelmente não poderão reembolsar o empréstimo.
Resuma as conclusões deste exemplo simples. Tome um ponto
M(x1,x2) e, substituindo as coordenadas do ponto na equação correspondente da reta
f(w,xi)=w0+w1xi1+w2xi2 , considere três opções:
- Se o ponto estiver abaixo da linha, e o atribuímos à classe +1 , então o valor da função f(w,xi)=w0+w1xi1+w2xi2 será positivo de 0 antes + infty . Portanto, podemos assumir que a probabilidade de reembolso do empréstimo está dentro (0,5,1] . Quanto maior o valor da função, maior a probabilidade.
- Se o ponto estiver acima da linha e o relacionarmos com a classe −1 ou 0 , o valor da função será negativo de 0 antes − infty . Então assumiremos que a probabilidade de pagamento da dívida está dentro [0,0,5) e, quanto maior o valor da função módulo, maior a nossa confiança.
- O ponto está em uma linha reta, na fronteira entre duas classes. Nesse caso, o valor da função f(w,xi)=w0+w1xi1+w2xi2 será igual 0 e a probabilidade de reembolso do empréstimo é igual a 0,5 .
Agora, imagine que não temos dois fatores, mas dezenas, tomadores de empréstimos, não três, mas milhares. Então, em vez de uma linha reta, teremos um plano e coeficientes
m-dimensionais w seremos retirados não do teto, mas retirados de acordo com todas as regras, mas com base nos dados acumulados sobre os mutuários que retornaram ou não devolveram o empréstimo. E realmente, lembre-se, agora estamos selecionando devedores com índices já conhecidos
w . De fato, a tarefa do modelo de regressão logística é precisamente determinar os parâmetros
w no qual o valor da função de perda
Logistic Loss tenderá a um mínimo. Mas como o vetor é calculado
vecw , ainda descobrimos na 5ª seção do artigo. Enquanto isso, retornamos à terra prometida - ao nosso banqueiro e seus três clientes.
Graças à função
f(w,xi)=w0+w1xi1+w2xi2 sabemos quem pode receber um empréstimo e quem precisa ser recusado. Mas você não pode consultar o diretor com essas informações, porque eles queriam obter a probabilidade de um pagamento de empréstimo de cada mutuário conosco. O que fazer A resposta é simples - precisamos transformar a função de alguma forma
f(w,xi)=w0+w1xi1+w2xi2 cujos valores estão no intervalo
(− infty,+ infty) em uma função cujos valores estarão no intervalo
[0,1] . E essa função existe, é chamada
função de resposta logística ou conversão de logit reverso . Conheça:
sigma( vecwT vecxi)= frac11+e− vecwT vecxi
Vamos dar uma olhada nas etapas para obter
a função de resposta logística . Observe que daremos um passo na direção oposta, ou seja, assumimos que sabemos o valor da probabilidade, que se situa na faixa de
0 antes
1 e então "giraremos" esse valor em todo o intervalo de números de
− infty antes
+ infty .
03. Saída da função de resposta logística
Etapa 1. Transfira os valores de probabilidade para o intervalo [0,+ infty)
No momento da transformação da função
f(w,xi)=w0+w1xi1+w2xi2 para
a função de resposta logística sigma( vecwT vecxi)= frac11+e vecwT vecxi deixaremos nosso analista de crédito em paz e passaremos pelas casas de apostas. Não, é claro, não faremos apostas, tudo o que nos interessa é o significado da expressão, por exemplo, uma chance de 4 para 1. As chances familiares a todos os jogadores de apostas são a proporção de "sucessos" e "fracassos". Em termos de probabilidades, as probabilidades são a probabilidade de ocorrência de um evento, dividida pela probabilidade de o evento não ocorrer. Nós escrevemos a fórmula para a chance de um evento
(probabilidades+) :
odds+= fracp+1−p+
onde
p+ - probabilidade de ocorrência de um evento,
(1−p+) - probabilidade de NÃO ocorrência de um evento
Por exemplo, se a probabilidade de um cavalo jovem, forte e espirituoso, apelidado de "Veterok", vencer nas corridas, uma velha velha e flácida apelidada de "Matilda" é igual a

, então as chances de sucesso da Veterka serão
4 para
1(0,8/(1−0,8)) e vice-versa, sabendo as chances, não será difícil calcular a probabilidade
p+ :
fracp+1−p+=4 mkern15mu Longrightarrow mkern15mup+=4(1−p+) mkern15mu Longrightarrow mkern15mu5p+=4 mkern15mu Longrightarrow mkern15mup+=0,8Assim, aprendemos a "traduzir" probabilidade em probabilidades que tiram valores de
0 antes
+ infty . Vamos dar mais um passo e aprender a "traduzir" a probabilidade para toda a linha numérica de
− infty antes
+ infty .
Etapa 2. Traduzimos os valores de probabilidade no intervalo (− infty,+ infty)
Este passo é muito simples - nós antecipamos as probabilidades com base no número de Euler
e e obtenha:
f(w,xi)= vecwT vecx=ln(probabilidades+)
Agora sabemos que se
p+=0,8 então calcule o valor
f(w,xi) será muito simples e, além disso, deve ser positivo:
f(w,xi)=ln(probabilidades+)=ln(0.8/0.2)=ln(4) approx+1.3862 . Assim é.
Por uma questão de curiosidade, verificamos que, se
p+=0,2 então esperamos ver um valor negativo
f(w,xi) . Verificamos:
f(w,xi)=ln(0,2/0,8)=ln(0,25) aprox−1,38629 . Tudo bem.
Agora sabemos como converter o valor da probabilidade de
0 antes
1 na linha de número inteiro de
− infty antes
+ infty . No próximo passo, faremos o oposto.
Enquanto isso, observamos que, de acordo com as regras do logaritmo, conhecendo o valor da função
f(w,xi) , você pode calcular as probabilidades:
odds+=ef(w,xi)=e vecwT vecx
Esse método de determinação de chances será útil na próxima etapa.
Etapa 3. Derivamos uma fórmula para determinar p+
Então aprendemos, sabendo
p+ encontrar valores de função
f(w,xi) . No entanto, de fato, precisamos de tudo exatamente o oposto - conhecer o valor
f(w,xi) encontrar
p+ . Para fazer isso, passamos a um conceito como a função inversa das chances, de acordo com a qual:
p+= fracodds+1+odds+
No artigo, não derivaremos a fórmula acima, mas verifique os números do exemplo acima. Sabemos que com probabilidades de 4 a 1 (
probabilidades+=$ ), a probabilidade de ocorrência de um evento é de 0,8 (
p+=0,8 ) Vamos fazer uma substituição:
p+= frac41+4=0,8 . Isso coincide com nossos cálculos realizados anteriormente. Nós seguimos em frente.
Na última etapa, deduzimos que
odds+=e vecwT vecx , o que significa que você pode fazer uma substituição na função inversa das probabilidades. Temos:
p+= frace vecwT vecx1+e vecwT vecx
Divida o numerador e o denominador por
e vecwT vecx então:
p+= frac11+e− vecwT vecx= sigma( vecwT vecx)
Para todo bombeiro, para garantir que não cometemos nenhum erro em nenhum lugar, faremos mais uma pequena verificação. Na etapa 2, somos a favor
p+=0,8 determinou que
f(w,xi) aprox+1,38829 . Então, substituindo o valor
f(w,xi) na função de resposta logística, esperamos obter
p+=0,8 . Substitua e obtenha:
p+= frac11+e−1,38829=0,8Parabéns, caro leitor, acabamos de desenvolver e testar a função de resposta logística. Vamos olhar para o gráfico da função.
Quadro 3 “Função de resposta logística”

Código para plotagem import math def logit (f): return 1/(1+math.exp(-f)) f = np.arange(-7,7,0.05) p = [] for i in f: p.append(logit(i)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$') plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16) plt.ylabel('$p_{i+}$', size = 16) plt.legend(prop = {'size': 14}) plt.show()
Na literatura, você também pode encontrar o nome dessa função como uma
função sigmóide . O gráfico mostra claramente que a principal mudança na probabilidade de pertencer a um objeto a uma classe ocorre em um intervalo relativamente pequeno
f(w,xi) em algum lugar de
−4 antes
+4 .
Proponho retornar ao nosso analista de crédito e ajudá-lo a calcular a probabilidade de reembolso dos empréstimos, caso contrário, ele corre o risco de ficar sem bônus :)
Quadro 2 "Potenciais tomadores de empréstimos"
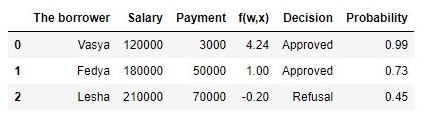
Código para gerar a tabela proba = [] for i in df['f(w,x)']: proba.append(round(logit(i),2)) df['Probability'] = proba df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]
Assim, determinamos a probabilidade de reembolso do empréstimo. Em suma, isso parece ser verdade.
De fato, a probabilidade de Vasya, com um salário de 120.000 R, poder doar 3.000 R mensalmente ao banco é quase 100%. A propósito, devemos entender que o banco também pode conceder um empréstimo à Lesha se a política do banco fornecer, por exemplo, empréstimos a clientes com probabilidade de reembolso do empréstimo maior que, digamos, 0,3. Nesse caso, o banco formará uma reserva maior para possíveis perdas.
Deve-se notar também que a relação salário / pagamento de pelo menos 3 e com uma margem de 5.000 foi retirada do teto. Portanto, não podemos usar o vetor de peso em sua forma original
vecw=(−5000,1,−3) . Precisávamos reduzir bastante os coeficientes e, nesse caso, dividimos cada coeficiente por 25.000, ou seja, ajustamos o resultado. Mas isso foi feito de propósito para simplificar a compreensão do material no estágio inicial. Na vida, não precisamos inventar e ajustar os coeficientes, mas encontrá-los. Apenas nas próximas seções do artigo, derivaremos as equações com as quais os parâmetros são selecionados
vecw .
04. Método dos mínimos quadrados para determinar o vetor de pesos vecw na função de resposta logística
Já conhecemos esse método para selecionar um vetor de peso
vecw como
o método dos mínimos quadrados (OLS) e, de fato, por que não o usamos em problemas de classificação binária? De fato, nada impede o uso de
EMNs , apenas esse método em problemas de classificação fornece resultados menos precisos que a
Perda Logística . Há uma justificativa teórica para isso. Vamos começar examinando um exemplo simples.
Suponha que nossos modelos (usando
MSE e
Logistic Loss ) já tenham iniciado a seleção do vetor de peso
vecw e paramos o cálculo em alguma etapa. Não importa, no meio, no final ou no começo, o principal é que já temos alguns valores do vetor de pesos e suponhamos, nesta etapa, o vetor de pesos
vecw para ambos os modelos não têm diferenças. Depois, pegamos os pesos obtidos e os substituímos na
função de resposta logística (
frac11+e− vecwT vecx ) para algum objeto que pertence à classe
+1 . Investigaremos dois casos quando, de acordo com o vetor selecionado de pesos, nosso modelo estiver muito equivocado e vice-versa - o modelo está fortemente confiante de que o objeto pertence à classe
+1 . Vamos ver quais multas serão "emitidas" ao usar
MNCs e
Logistic Loss .
Código para calcular multas, dependendo da função de perda usada O caso com um erro grave - o modelo classifica o objeto
+1 com uma probabilidade de 0,01
A penalidade ao usar o
OLS é:
MSE=(y−p+)=(1−0,01)2=0,9801A penalidade ao usar a
perda logística é:
LogLoss=loge(1+e−yf(w,x))=loge(1+e−1(−4.595...)) aproximadamente4.605Caso com forte certeza - o modelo classifica o objeto
+1 com uma probabilidade de 0,99
A penalidade ao usar o
OLS é:
MSE=(1−0,99)2=$0,000A penalidade ao usar a
perda logística é:
Perdadelog=loge(1+e−4.595...) aproximadamente0,01Este exemplo ilustra bem que, com um erro grosseiro, a função de perda de
perda de log multas o modelo significativamente mais do que
MSE . Vamos agora entender quais são os pré-requisitos teóricos para usar a função de perda de
perda de log em problemas de classificação.
05. Método de máxima credibilidade e regressão logística
Como prometido no início, o artigo está repleto de exemplos simples. No estúdio, outro exemplo e clientes antigos são os mutuários do banco: Vasya, Fedya e Lesha.
Para todo bombeiro, antes de desenvolver um exemplo, lembre-se de que na vida estamos lidando com uma amostra de treinamento de milhares ou milhões de objetos com dezenas ou centenas de sinais. No entanto, aqui os números são tomados para que eles se encaixem facilmente na cabeça de um teste de dados iniciante.
Voltamos por exemplo. Imagine que o diretor do banco decidiu conceder um empréstimo a todos os necessitados, apesar do fato de o algoritmo sugerir não concedê-lo a Lesha. E então passou o tempo suficiente e ficamos cientes de quais dos três heróis reembolsaram o empréstimo e quem não o fez. O que era de se esperar: Vasya e Fedya pagaram o empréstimo, mas Alex não. Agora vamos imaginar que esse resultado será uma nova amostra de treinamento para nós e, ao mesmo tempo, todos os dados sobre os fatores que afetam a probabilidade de pagamento do empréstimo (salário do mutuário, valor do pagamento mensal) parecem ter desaparecido. Então, intuitivamente, podemos assumir que todo terceiro tomador de empréstimo não devolve um empréstimo ao banco ou, em outras palavras, a probabilidade de um empréstimo ser devolvido pelo próximo tomador de empréstimo.
p= frac23 . Há evidências teóricas para essa suposição intuitiva e é baseada no
método da
máxima verossimilhança , frequentemente referido na literatura como
o princípio da máxima verossimilhança .
Primeiro, familiarize-se com o aparato conceitual.
A probabilidade de uma
amostra é a probabilidade de obter exatamente essa amostra, de obter exatamente essas observações / resultados, ou seja, o produto das probabilidades de obter cada um dos resultados da amostra (por exemplo, o empréstimo de Vasya, Feday e Lesha ao mesmo tempo foi reembolsado ou não).
A função de probabilidade associa a probabilidade de uma amostra aos valores dos parâmetros de distribuição.
No nosso caso, a amostra de treinamento é um esquema generalizado de Bernoulli, no qual uma variável aleatória assume apenas dois valores:
1 ou
0 . Portanto, a probabilidade da amostra pode ser escrita como uma função da probabilidade do parâmetro
p da seguinte maneira:
P( mkern5mu vecy mkern5mu| mkern5mup)= prod limits3i=1pyi(1−p)(1−yi) mkern5mu= mkern5mup1(1−p)1−1 centerdotp1(1−p)1−1 centerdotp0(1−p)1−0 mkern5mu== mkern5mup centerdotp centerdot(1−p) mkern5mu= mkern5mup2(1−p)O registro acima pode ser interpretado da seguinte maneira. A probabilidade conjunta de que Vasya e Fedya reembolsarão o empréstimo é igual a
p c e n t e r d o t p = p 2 , a probabilidade de Alex NÃO reembolsar o empréstimo é

(como NÃO foi o pagamento do empréstimo), portanto, a probabilidade conjunta dos três eventos é
p 2 ( 1 - p ) .
O método de máxima verossimilhança é um método para estimar um parâmetro desconhecido, maximizando a função de verossimilhança . No nosso caso, precisamos encontrar esse valorp em queP (→ y|p ) = p 2 ( 1 - p ) atinge o máximo.De onde vem a idéia - procurar o valor de um parâmetro desconhecido no qual a função de probabilidade atinge um máximo? As origens da idéia decorrem da noção de que a amostragem é a única fonte de conhecimento disponível para nós sobre a população em geral. Tudo o que sabemos sobre a população é apresentado na amostra. Portanto, tudo o que podemos dizer é que a amostra é o reflexo mais preciso da população que está disponível para nós. Portanto, precisamos encontrar um parâmetro no qual a amostra disponível se torne a mais provável.Obviamente, estamos lidando com um problema de otimização no qual é necessário encontrar o ponto extremo de uma função. Para encontrar o ponto extremo, é necessário considerar uma condição de primeira ordem, ou seja, equiparar a derivada da função a zero e resolver a equação com relação ao parâmetro desejado. No entanto, a busca pela derivada de um produto de um grande número de fatores pode ser longa, portanto, existe uma técnica especial para evitar isso - a transição para o logaritmo da função de probabilidade . Por que essa transição é possível? Prestamos atenção ao fato de que não estamos procurando o extremo da própria funçãoP (→ y|p ) , e o ponto extremo, ou seja, o valor do parâmetro desconhecidop em queP (→ y|p ) atinge o máximo. Na transição para o logaritmo, o ponto extremo não muda (embora o próprio extremo seja diferente), uma vez que o logaritmo é uma função monotônica. De acordo com o exposto, continuemos a desenvolver nosso exemplo de empréstimos com a Vasya, Fedi e Lesha. Primeiro, vamos aologaritmo da função de probabilidade:l o g P (→ y|p )=l o g p 2 ( 1 - p )=2 l o g p + l o g ( 1 - p ) Agora podemos diferenciar facilmente a expressão porp :∂ l o g P (→ y|p )∂ p=∂∂ p (2lSgp+log(1-P))=2p -11 - p E finalmente, considere a condição de primeira ordem - equiparamos a derivada da função a zero:2p -11 - p =0⟹2p =11 - p⟹2 ( 1 - p ) = p⟹p = 23 Assim, nossa avaliação intuitiva da probabilidade de pagamento de empréstimosp = 23 foi teoricamente fundamentado. Ótimo, mas o que fazemos agora com essa informação? Se assumirmos que cada terceiro tomador do empréstimo não devolve dinheiro ao banco, este último inevitavelmente irá à falência. E assim é, mas apenas ao avaliar a probabilidade de reembolso de um empréstimo igual a23 não levamos em consideração os fatores que afetam o reembolso do empréstimo: o salário do tomador e o tamanho do pagamento mensal. Lembre-se de que calculamos anteriormente a probabilidade de pagamento de empréstimos por cada cliente, levando em consideração esses fatores. É lógico que as probabilidades que obtivemos sejam diferentes da constante igual a23 .
Vamos determinar a probabilidade das amostras:Código para calcular a probabilidade de amostras from functools import reduce def likelihood(y,p): line_true_proba = [] for i in range(len(y)): ltp_i = p[i]**y[i]*(1-p[i])**(1-y[i]) line_true_proba.append(ltp_i) likelihood = [] return reduce(lambda a, b: a*b, line_true_proba) y = [1.0,1.0,0.0] p_log_response = df['Probability'] const = 2.0/3.0 p_const = [const, const, const] print ' p=2/3:', round(likelihood(y,p_const),3) print '****************************************************************************************************' print ' p:', round(likelihood(y,p_log_response),3)
A probabilidade de amostragem a um valor constante p = 23 :P (→ y|p )=p 2 ( 1 - p )=23 2(1-23 )≈0.148→x :P(→y|p)=3∏i=1pyi(1−p)(1−yi)=p11(1−p1)1−1⋅p12(1−p2)1−1⋅p03(1−p3)1−0==p1⋅p2⋅(1−p3)=0.99⋅0.73⋅(1−0.45)≈0,397 A probabilidade de uma amostra com probabilidade calculada dependendo de fatores acabou sendo maior que a probabilidade com um valor constante de probabilidade. Do que isso está falando? Isso sugere que o conhecimento dos fatores tornou possível selecionar com mais precisão a probabilidade de pagamento do empréstimo para cada cliente. Portanto, ao emitir outro empréstimo, será mais correto usar o modelo para avaliar a probabilidade de pagamento da dívida proposta no final da 3ª seção do artigo. Mas então, se precisarmos maximizara função de probabilidade da amostra, por que não usar um algoritmo que fornecerá as probabilidades para Vasya, Fedi e Lesha, por exemplo, iguais a 0,99, 0,99 e 0,01, respectivamente. Talvez esse algoritmo se mostre bem na amostra de treinamento, pois trará o valor da probabilidade da amostra para mais perto1 , mas, em primeiro lugar, esse algoritmo provavelmente terá dificuldades com a capacidade de generalização e, em segundo lugar, esse algoritmo definitivamente não será linear. E se os métodos de lidar com a reciclagem (capacidade de generalização igualmente fraca) claramente não estão incluídos no plano deste artigo, passemos ao segundo parágrafo com mais detalhes. Para fazer isso, basta responder a uma pergunta simples. A probabilidade de reembolso de um empréstimo à Vasya e à Feday pode ser a mesma, levando em consideração os fatores conhecidos por nós? Do ponto de vista da lógica sonora, é claro que não, não pode. Então, Vasya dará 2,5% de seu salário por mês para pagar o empréstimo, e Fedya - quase 27,8%. Também no gráfico 2 "Classificação de clientes", vemos que Vasya está muito mais distante da linha que separa classes do que Fedya. E, finalmente, sabemos que a funçãof ( w , x ) = w 0 + w 1 x 1 + w 2 x 2 para Vasya e Fedi assume valores diferentes: 4,24 para Vasya e 1,0 para Fedi. Agora, se a Fedya, por exemplo, recebesse uma ordem de magnitude mais ou pedisse um empréstimo menor, as probabilidades de pagar o empréstimo da Vasya e da Fedi seriam semelhantes. Em outras palavras, um relacionamento linear não pode ser enganado. E se realmente calculássemos as chancesw , mas não os tiramos do teto, poderíamos declarar com segurança que nossos valoresw melhor nos permite estimar a probabilidade de pagamento de empréstimos por cada mutuário, mas desde que concordamos em considerar que a determinação dos coeficientesw foi realizado de acordo com todas as regras, assumiremos que sim - nossos coeficientes nos permitem dar uma estimativa melhor da probabilidade :)No entanto, estávamos distraídos. Nesta seção, precisamos entender como o vetor de pesos é determinado→ w , que é necessário para avaliar a probabilidade de retorno de um empréstimo por cada mutuário. Resumir brevemente qual o arsenal que estamos procurandow :1. Assumimos que a relação entre a variável alvo (valor previsto) e o fator que influencia o resultado é linear. Por esse motivo,a função de regressão linear doformulário é usada.f ( w , x ) = → w T X , cuja linha divide objetos (clientes) em classes+ 1 e- 1 ou0 (clientes que podem pagar o empréstimo e não podem). No nosso caso, a equação tem a formaf ( w , x ) = w 0 + w 1 x 1 + w 2 x 2 .
2. Usamos a função de transformação inversa de log do formuláriop + = 11 + e - → w T → x =σ( → w T → x )para determinar a probabilidade de o objeto pertencer à classe+ 1 .
3. Consideramos nossa amostra de treinamento como a implementação de um esquema generalizado de Bernoulli , ou seja, para cada objeto é gerada uma variável aleatória, com probabilidadep (próprio para cada objeto) assume o valor 1 e com probabilidade( 1 - p ) - 0.4. Sabemos que precisamos maximizara função de probabilidade da amostra, levando em consideração os fatores aceitos, para que a amostra existente se torne a mais provável. Em outras palavras, precisamos selecionar esses parâmetros nos quais a amostra será a mais plausível. No nosso caso, o parâmetro selecionado é a probabilidade de reembolso do empréstimop , que por sua vez depende de coeficientes desconhecidosw .
Então, precisamos encontrar esse vetor de pesos → w , em que a probabilidade de amostragem será máxima. 5. Sabemos que, para maximizara função de probabilidade de uma amostra,você pode usaro método de probabilidade máxima. E sabemos todos os truques para trabalhar com esse método. Aqui está um caminho múltiplo :)E lembre-se de que, no início do artigo, queríamos derivar dois tipos da função de perda deperda logística, dependendo de como as classes de objetos são designadas. Ocorreu que em problemas de classificação com duas classes, as classes são denotadas como+ 1 e0 ou- 1 .
Dependendo da designação, a saída terá uma função de perda correspondente.Caso 1. Classificação de objetos em + 1 e0 0
Anteriormente, ao determinar a probabilidade de uma amostra em que a probabilidade de pagamento da dívida pelo mutuário fosse calculada com base em fatores e coeficientes especificados w , aplicamos a fórmula:P (→ y|p ) = 3 ∏ i = 1 p y i ( 1 - p ) ( 1 - y i ) Realmentep i é o valor dafunção de resposta logística p + = 11 + e - → w T → x =σ( → w T → x )para um determinado vetor de peso→ w Então nada nos impede de escrever a função de probabilidade da amostra assim:P (→ y|σ ( → w T X ) )=n ∏ i = 1 σ( → w T → x i ) y i( 1 - σ ( → w T → x i ) ( 1 - y i )→m a x
Acontece que, às vezes, para alguns analistas iniciantes, é difícil entender imediatamente como essa função funciona. Vejamos 4 exemplos curtos que esclarecerão tudo:1. Sey i = + 1 (ou seja, de acordo com a amostra de treinamento, o objeto pertence à classe +1) e nosso algoritmoσ ( → w T X ) ) determina a probabilidade de classificação de um objeto+ 1 igual a 0,9, a probabilidade dessa amostra será calculada da seguinte forma:0,9 1 ⋅ ( 1 - 0,9 ) ( 1 - 1 ) = 0,9 1 ⋅ 0,1 0 = 0,9 2.Sey i = + 1 , eσ ( → w T X ) ) = 0,1 , então o cálculo será o seguinte:0,1 1 ⋅ ( 1 - 0,1 ) ( 1 - 1 ) = 0,1 1 ⋅ 0,9 0 = 0,1 3.Sey i = 0 eσ ( → w T X ) ) = 0,1 , então o cálculo será o seguinte:0,1 0 ⋅ ( 1 - 0,1 ) ( 1 - 0 ) = 0,1 0 ⋅ 0,9 1 = 0,9 4.Sey i = 0 eσ ( → w T X ) ) = 0,9 , então o cálculo será o seguinte:0,9 0 ⋅ ( 1 - 0,9 ) ( 1 - 0 ) = 0,9 0 ⋅ 0,1 1 = 0,1 É óbvio que a função de probabilidade será maximizada nos casos 1 e 3 ou no caso geral com valores adivinhados corretamente das probabilidades de classificar um objeto como uma classe+ 1 .
Devido ao fato de que ao determinar a probabilidade de classificar um objeto como uma classe + 1 não sabemos apenas os coeficientesw , então vamos procurá-los. Como mencionado acima, esse é um problema de otimização, no qual precisamos primeiro encontrar a derivada da função de probabilidade com relação ao vetor de pesow .
No entanto, faz sentido simplificar a tarefa primeiro: buscaremos a derivada do logaritmo da função de probabilidade .L l o g ( X , → y , → w ) = n ∑ i = 1 ( - y il o g eσ ( → w T → x i ) - ( 1 - y i )l o g e( 1 - σ ( → w T → x i ) ) ) → m i n
Por que, após o logaritmo, na função do erro logístico , alteramos o sinal com+ on- .
Tudo é simples, uma vez que é costume minimizar o valor de uma função em problemas de avaliação da qualidade do modelo, multiplicamos o lado direito da expressão por - e consequentemente, em vez de maximizar, agora minimizamos a função. Na verdade, agora, diante de seus olhos, a função de perda - aPerda Logísticapara o conjunto de treinamento com duas classesfoi muito sofrida.+ 1 e0 0 .
Agora, para encontrar os coeficientes, basta encontrar a derivada da função de erro logístico e, usando métodos de otimização numérica, como descida de gradiente ou descida de gradiente estocástico, selecione os coeficientes mais ideaisw .
Porém, dado o tamanho já pequeno do artigo, propõe-se diferenciar de forma independente ou, talvez, este seja o tópico para o próximo artigo com muita aritmética sem exemplos detalhados.Caso 2. Classificação de objetos em + 1 e- 1
A abordagem aqui será a mesma das classes 1 e0 , mas o próprio caminho para a saída da função de perda deperda logísticaserá mais ornamentado. Descer. Para a função de probabilidade, usamos o operador"if ... then ...". Ou seja, sei- ésimo objeto pertence à classe+ 1 , para calcular a probabilidade da amostra, usamos a probabilidadep se o objeto pertencer à classe- 1 , então, na verossimilhança, substituímos( 1 - p ) .
É assim que a função de probabilidade se parece:P (→ y|σ ( → w T X ) )=n ∏ i = 1 σ( → w T → x i )[ y i =+1]( 1 - σ ( → w T → x i ) [ y i = - 1 ] )→m a x
Vamos escrever nos dedos como isso funciona. Considere 4 casos:1. Sey i = + 1 eσ ( → w T → x i ) = 0,9 , então a "probabilidade" da amostra "vai"0,9 2.Sey i = + 1 eσ ( → w T → x i ) = 0,1 , então "irá para a probabilidade da amostra"0.1 3.Sey i = - 1 eσ ( → w T → x i ) = 0,1 , então "irá para a probabilidade da amostra"1 - 0,1 = 0,9 4.Sey i = - 1 eσ ( → w T → x i ) = 0,9 , então a "probabilidade" da amostra "vai"1 - 0,9 = 0,1 É óbvio que nos casos 1 e 3, quando as probabilidades foram determinadas corretamente pelo algoritmo,a função de probabilidadeserá maximizada, ou seja, é isso que queremos obter. No entanto, essa abordagem é bastante complicada, e consideraremos uma gravação mais compacta abaixo. Mas primeiro, o logaritmo da probabilidade funciona com uma mudança de sinal, já que agora o minimizaremos.L l o g ( X , → y , → w ) = n ∑ i = 1 ( - [ y i = + 1 ]l o g eσ ( → w T → x i ) - [ y i = - 1 ]l o g e( 1 - σ ( → w T → x i ) ) ) → m i n
Substitua em vez disso σ ( → w T → x i ) a expressão11 + e - → w T → x i :Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(1−11 + e - → w T → x i ))→min
Simplifique o termo correto sob o logaritmo usando técnicas aritméticas simples e obtenha:L l o g ( X , → y , → w ) = n ∑ i = 1 ( - [ y i = + 1 ]l o g e( 11 + e - → w T → x i )-[yi=-1]l o g e( 11 + e → w T → x i ))→min
E agora é hora de se livrar do operador "se ... então ..." . Observe que quando um objetoy eu pertenço à classe+ 1 , então na expressão sob o logaritmo, no denominador,e é criado- → w T → x i se o objeto pertencer à classe- 1 , então $ e $ é elevado a uma potência+ → w T → x i .
Portanto, escrever um diploma pode ser simplificado combinando os dois casos em um: - y i → w T → x i .
Em seguida, a função de erro logístico assume o formato:L l o g ( X , → y , → w ) = n ∑ i = 1 -l o g e( 11 + e - y i → w T → x i )→min
De acordo com as regras do logaritmo, vire a fração e retire o sinal " - "(menos) para o logaritmo, obtemos:L l o g ( X , → y , → w ) = n ∑ i = 1l o g e( 1 + e - y i → w T → x i ) → m i n
Aqui está a função de perda logística , que é usada no conjunto de treinamento com objetos relacionados às classes:+ 1 e- 1 .
Bem, neste momento eu me despedi e terminamos o artigo.← Trabalho anterior do autor - “Trazemos a equação de regressão linear para a forma matricial”Materiais de apoio
1. Literatura
1) Análise de regressão aplicada / N. Draper, G. Smith - 2ª ed. - M .: Finance and Statistics, 1986 (traduzido do inglês)2) Teoria da Probabilidade e Estatística Matemática / V.E. Gmurman - 9a ed. - M .: Escola Superior, 20033) Teoria da Probabilidade / N.I. Chernova - Novosibirsk: Novosibirsk State University, 20074) Análise de negócios: dos dados ao conhecimento / Paklin N. B., Oreshkov V. I. - 2nd ed. - São Petersburgo: Peter, 20135) Ciência de Dados Ciência de Dados a partir do zero / Joel Grass - São Petersburgo: BHV Petersburgo, 20176) Estatísticas práticas para especialistas em Ciência de Dados / P. Bruce, E. Bruce - São Petersburgo: BHV Petersburg, 20182. Palestras, cursos (vídeo)
1) A essência do método da máxima verossimilhança, Boris Demeshev2) O método da máxima verossimilhança, no caso contínuo, Boris Demeshev3) Regressão logística. Curso aberto ODS, Yury Kashnitsky4) Palestra 4, Evgeny Sokolov (com 47 minutos de vídeo)5) Regressão logística, Vyacheslav Vorontsov3. fontes da Internet
1) Modelos lineares de classificação e regressão2) É fácil entender a regressão logística3) Função logística do erro4) Testes independentes e fórmula de Bernoulli5) Balada do FMI6) Método de máxima verossimilhança7) Fórmulas e propriedades dos logaritmos8) Por que o número e ? 9) Classificador linear