Na véspera do início do curso “Matemática para Ciência de Dados. Curso Avançado ”, realizamos um webinar aberto sobre o tópico“ Métodos de Análise de Regressão em Ciência de Dados ”. Nele, nos familiarizamos com o conceito de regressões lineares, estudamos onde e como elas podem ser aplicadas na prática e também aprendemos quais tópicos e seções da análise matemática, álgebra linear e teoria das probabilidades são usados nessa área. Professor - Peter Lukyanchenko , professor da Escola Superior de Economia, chefe de projetos de tecnologia.
Se falamos de matemática no contexto da ciência de dados, podemos destacar os três problemas resolvidos com mais freqüência (embora haja, é claro, mais problemas):

Vamos falar sobre essas tarefas em mais detalhes:
- A tarefa de análise de regressão ou identificação de dependências (quando temos um determinado conjunto de observações). No gráfico acima, você pode ver que existe uma certa variável x e uma certa variável y, e observamos os valores de y para um x específico. Conhecemos esses pontos e suas coordenadas, e também sabemos que x de alguma forma afeta y, ou seja, essas duas variáveis são dependentes uma da outra. Naturalmente, queremos calcular a equação de sua dependência - para isso, usamos o modelo da regressão linear de pares clássicos , quando se assume que sua dependência pode ser descrita por uma certa linha reta. Consequentemente, os coeficientes da linha reta são selecionados de modo a minimizar o erro na descrição dos dados. E apenas sobre que tipo de erro (métrica de qualidade) será selecionado, o resultado real da construção de uma regressão linear depende.
- Outra tarefa da análise de dados são os sistemas de recomendação . É quando dizemos que existem, por exemplo, lojas on-line, elas têm um certo conjunto de mercadorias e uma pessoa faz compras. Com base nessas informações, é possível fornecer uma descrição dessa pessoa no espaço vetorial e, depois de construí-lo, criar uma dependência matemática da probabilidade com que essa pessoa comprará este ou aquele produto, conhecendo suas compras anteriores. Nesse sentido, estamos falando de classificação quando classificamos os compradores em potencial de acordo com os princípios: “não compre, não interesse”, etc. Existem várias abordagens: baseada no usuário e baseada no item.
- A terceira área é a visão computacional . No decorrer desta tarefa, estamos tentando determinar onde o objeto de interesse para nós está localizado. Esta é realmente uma solução para o problema de minimizar erros selecionando pixels específicos que formam a imagem do objeto.
Nos três problemas, há otimização, minimização de erros e a presença de um ou outro modelo que descreve a dependência de variáveis. Ao mesmo tempo, dentro de cada uma existe uma representação de dados que é decomposta em uma descrição vetorial. Em nosso artigo, prestaremos atenção especial à seção que afeta
os modelos de regressão .
Já mencionamos que existe um certo conjunto de pares de dados: X e Y. Sabemos quais valores Y leva em relação a X. Se X é tempo, obtemos um modelo de série temporal em que Y é, digamos, o preço do petróleo e, ao mesmo tempo, a taxa de câmbio entre rublo e dólar e X é um determinado período de tempo de 2014 a 2018:
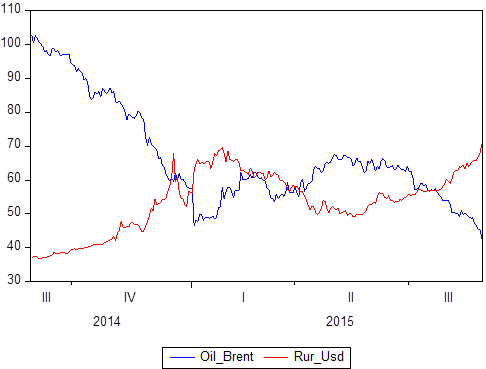
Se você criar graficamente, é claro que essas duas séries temporais são interdependentes. Depois de definir o conceito de correlação, é possível calcular o grau de dependência e, se souber que alguns valores estão perfeitamente correlacionados (a correlação é 1 ou -1), você pode usá-lo para tarefas de previsão ou para tarefas de descrição.
Considere a seguinte ilustração:
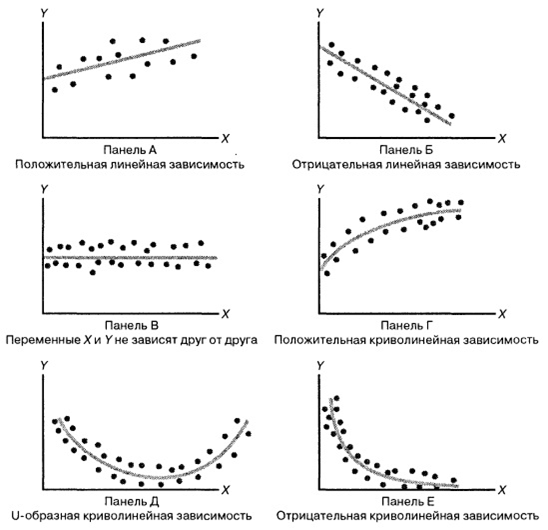
A parte mais difícil na formação de um modelo de regressão é
colocar inicialmente alguma função específica em sua memória . Por exemplo, para a Figura A é Y = kX + b, para B é Y = -kX + b, na figura C o "jogo" é igual a algum número, o gráfico na figura D provavelmente é baseado na raiz de " X ”, na base de D, possivelmente uma parábola, e na base de E - uma hipérbole.
Acontece que
escolhemos algum modelo de dependência de dados e os tipos de dependência entre variáveis aleatórias são diferentes. Tudo não é tão óbvio, porque mesmo nesses desenhos simples, vemos várias dependências. Ao escolher um relacionamento específico, podemos usar métodos de regressão para calibrar o modelo.
A qualidade das suas previsões dependerá do modelo escolhido . Se focarmos nos modelos de regressão linear, assumimos que existe um certo conjunto de valores reais:

A figura mostra os 4 valores observados de X1, X2, X2, X4. Para cada um dos X, o valor Y é conhecido (no nosso caso, estes são os pontos: P1, P2, P3, P4). Esses são os pontos que realmente observamos nos dados. Assim, recebemos um determinado conjunto de dados. E, por alguma razão, decidimos que a regressão linear descreve melhor a relação entre o X e o jogador. Além disso, toda a questão é como construir a equação de uma reta Y = b
1 + b
2 X, onde b
2 é a inclinação, b
1 é o coeficiente de interseção. A questão toda é qual
é o melhor conjunto de b
2 e b
1 para que esta linha reta descreva a relação entre essas variáveis com a maior precisão possível.
Os pontos R1, R2, R3, R4 são os valores que nosso modelo fornece nos valores de X. O que acontece? Os pontos P são pontos que realmente observamos (realmente coletados) e os pontos R são pontos que observamos em nosso modelo (aqueles que ele produz). O que se segue é uma lógica humana incrivelmente simples: um
modelo será considerado qualitativo se e somente se os pontos R estiverem o mais próximo possível dos pontos P.Se construirmos a distância entre esses pontos para o mesmo "X" (P
1 - R
1 , P
2 - R
2 , etc.), obteremos o que é chamado de erro de regressão linear. Obtemos os desvios na regressão linear, e esses desvios são chamados U
1 , U
2 , U
3 ... U
n . E esses erros podem ser positivos ou negativos (poderíamos superestimar ou subestimar). Para comparar esses desvios, eles precisam ser analisados. Um método muito grande e bonito é usado aqui - quadrado (quadrado “mata” o sinal). E a soma dos quadrados de todos os desvios nas estatísticas matemáticas é chamada RSS (soma residual dos quadrados). Ao minimizar o RSS em b
1 e ao minimizar o RSS em b
2 , obtemos coeficientes ótimos que são realmente derivados
pelo método dos mínimos quadrados .
Depois que construímos a regressão, determinamos os coeficientes ótimos b
1 eb
2 , e temos a equação de regressão, os problemas não terminam aí e o problema continua se desenvolvendo. O fato é que, se a própria regressão estiver marcada em um gráfico, com todos os valores que temos, assim como os valores médios dos “jogos”, a soma dos erros ao quadrado poderá ser esclarecida.
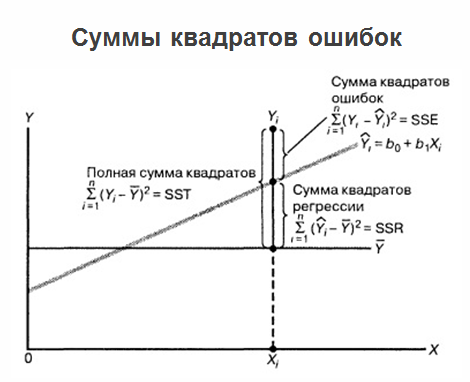
Ao mesmo tempo, é considerado útil exibir erros de previsão de regressão em relação à variável X. Veja a figura abaixo:

Tivemos algum tipo de regressão e extraímos os dados reais. Temos a distância de cada valor real até a regressão. E o desenhamos em relação ao valor zero para os valores correspondentes de X. Na figura acima, vemos uma imagem muito ruim: os
erros dependem de X. Alguma dependência de correlação é claramente expressa:
quanto mais longe o "X" nos movemos, maior a significância dos erros . Isso é muito ruim. A presença de correlação nesse caso indica que adotamos o modelo de regressão por engano e houve algum parâmetro em que “não pensamos” ou simplesmente perdemos de vista. Afinal, se todas as variáveis forem colocadas dentro do modelo, os erros devem ser completamente aleatórios e não devem depender de quais fatores são iguais.
Os erros devem ter a mesma distribuição de probabilidade , caso contrário, suas previsões serão erradas. Se você desenhou os erros do seu modelo no avião e encontrou um triângulo divergente, é melhor começar tudo do zero e recontar completamente o modelo.
Ao analisar os erros, você pode entender imediatamente imediatamente onde eles calcularam incorretamente, que tipo de erro eles cometeram. E aqui não podemos deixar de mencionar o teorema de Gauss-Markov:

O teorema determina as condições sob as quais as estimativas obtidas pelo método dos mínimos quadrados são as melhores, consistentes e efetivas na classe de estimativas lineares imparciais.
A conclusão pode ser tirada da seguinte forma: agora entendemos que a
área de construção de um modelo de regressão é, em certo sentido, o culminar do ponto de vista da matemática , porque mescla todas as seções possíveis ao mesmo tempo, o que pode ser útil na análise de dados, por exemplo:
- álgebra linear com métodos de representação de dados;
- análise matemática com teoria de otimização e meios de análise de funções;
- teoria das probabilidades com meios de descrever eventos e quantidades aleatórios e modelar a relação entre variáveis.
Colegas, sugiro a mesma coisa, não se limitando a ler e assistir ao webinar inteiro . O artigo não incluiu momentos relacionados à programação linear, otimização em modelos de regressão e outros detalhes que podem ser úteis para você.