Geekly articles weekly

原位传感器校准注意事项

在安装到板上后，某些加速度传感器需要额外的零位校准。当我看到一些加速度传感器校准的数据源时，仅通过从Z轴减去9.8 m / s2的值就将G分量考虑在内，便想到了编写此注释的想法。




出版结构


  • 问题
  • 问题陈述和解决方法
  • 如何获得积分？
  • 如何计算球的中心？
  • 如何加快寻找球心的速度？
  • 还有什么其他方法来加快对球中心的搜索？
  • 关于测量误差
  • 总


问题


问题是什么-MEMS传感器在板中安装后会发生轻微变形，从而影响：
  • 零位
  • 测量值的缩放；
  • 轴彼此之间的垂直度。

如果不是很明显地违反了缩放和垂直性，则零位的位置会被缠结。例如，如果将MPU9250传感器的加速度计零偏移量的典型值转换为m / s 2，则可以在0.2 m / s 2的范围内获得该值。也就是说，传感器是固定的，但是它显示出加速度，并且在5秒钟后，我们获得了1 m / s的速度。一方面，所有传感器数据总是通过某种过滤器（例如）传递。但是，另一方面，滤波器为什么要不断补偿这种偏差呢？毕竟，传感器会显示出它不在的位置。这降低了结果的准确性。总而言之，您需要一次找到偏移值，然后在传感器运行期间从其读数中减去该值。

立即想到的寻找零偏移量的最简单解决方案是创建传感器必须精确显示零的条件。传感器上记录的值是零偏移的值！所以？但是，没有-重力不断作用于加速度计。为了避免这种情况，将需要失重（抛掷将不起作用）。地球磁场作用于罗盘，其旋转作用于陀螺仪。因此，如果您没有个人飞船，就必须想出一些办法。

立即想到的第二个解决方案是将传感器（或更确切地说是其轴）放置在我们确切知道传感器应显示什么位置的位置。传感器显示的内容与应显示的内容之间的差异-偏移量为零！所以？例如，我们知道，如果将加速度计放在水平线上，那么理论上，重力加速度矢量将精确地沿传感器的Z轴定向。我们知道的加速度矢量的大小。

但是，有一个问题。这是因为我们无法将传感器的轴精确地设置为与水平线齐平。事实是，我们将依靠的表面不平行于印刷电路板。这又不平行于传感器所在的位置。传感器本身并不完全位于其位置，并且传感器内部的轴不平行于传感器主体。将轴相对于水平线设置1度时出现错误，导致投影的大小与我们要查找的零偏移本身的值相当。在磁力计的情况下，我们也不知道磁场矢量的方向。理论上讲北方。但实际上，地球磁场本身在强度和方向上是异质的。另外，附近的金属物体也会进行调整。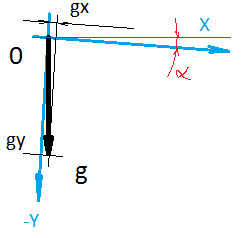


问题陈述和解决方法


任务如下：我们需要使用传感器确定零位移矢量，该传感器将始终记录位移矢量+恒定的外部冲击矢量（重力加速度，地球自转，地球磁场），而幅度和方向是未知的（对于加速度计而言）我们知道该值，但同样，传感器的比例可能不等于1）。

解决的方法。本文提出如下确定位移矢量。我们以各种方式拿起并扭曲传感器，并记录传感器读数。经过N次测量后，从传感器获取并位于图表上的值将是一个球，其半径是外部撞击的幅度，而中心是精确的所需零偏移量。

如何获得积分？


为了简化测量过程本身，您可以编写一个简单的程序。当设备静止时，它应该记录传感器。我们只需要将设备转到所需位置即可。为了确定静止状态，还可以使用未校准的加速度计-只需取当前值与前一个值之间的差即可。如果有更多的噪音，那么我们将修复机芯。我的阈值在0.07G左右。如果您用手握住，结果将超出此值。我用胶带固定了位置。如果仍然无法解决问题，请检查附近是否有冰箱，风扇或类似物品。
怎么在代码中
//       
static TSumSensorsData 	g_sens_data[2];
static int32_t   	g_sens_data_sum_cnt[2];
static uint8_t		g_sens_data_num;

//  - ,     
IS_INTERRUPT void on_dma_raw_ready_calibrate_step1()
{
	SensorRawBuffer *raw = sensor_get_raw_buffer();
	g_sens_data[g_sens_data_num].acc_x += swap_i16(raw->accell_x_unswap);
	g_sens_data[g_sens_data_num].acc_y += swap_i16(raw->accell_y_unswap);
	g_sens_data[g_sens_data_num].acc_z += swap_i16(raw->accell_z_unswap);
	g_sens_data[g_sens_data_num].gyro_x += swap_i16(raw->gyro_x_unswap);
	g_sens_data[g_sens_data_num].gyro_y += swap_i16(raw->gyro_y_unswap);
	g_sens_data[g_sens_data_num].gyro_z += swap_i16(raw->gyro_z_unswap);
	g_sens_data[g_sens_data_num].mag_x += raw->mag_x_raw * g_mag_calibrate.kx;
	g_sens_data[g_sens_data_num].mag_y += raw->mag_y_raw * g_mag_calibrate.ky;
	g_sens_data[g_sens_data_num].mag_z += raw->mag_z_raw * g_mag_calibrate.kz;
	g_sens_data_sum_cnt[g_sens_data_num]++;
}

//   main
void sensors_calibrate_program(FlashROM *flash_ptr)
{
	double calibrate_result_error[3];
	TVector16 calibrate_result[3];
	int32_t radius[ACCEL_NO_MOTION_DETECT_COUNT];
	uint8_t raw_is_deleted[ACCEL_NO_MOTION_DETECT_COUNT];
	TVector16 raw[3][ACCEL_NO_MOTION_DETECT_COUNT];
	
        . . .

	//  
	g_sens_data_sum_cnt[0] = 0;
	g_sens_data_num = 0;
	int16_t prev_avg_x = 0;
	int16_t prev_avg_y = 0;
	int16_t prev_avg_z = 0;
	int8_t low_motion_cnt = 0;

	while(low_motion_cnt < ACCEL_NO_MOTION_DETECT_COUNT)
	{
		if (g_sens_data_sum_cnt[g_sens_data_num] >= ACCEL_NO_MOTION_DETECT_SAMPLES)
		{
			uint8_t new_data_num = (g_sens_data_num + 1) & 1;
			g_sens_data[new_data_num].acc_x = 0;
			g_sens_data[new_data_num].acc_y = 0;
			g_sens_data[new_data_num].acc_z = 0;
			g_sens_data[new_data_num].gyro_x = 0;
			g_sens_data[new_data_num].gyro_y = 0;
			g_sens_data[new_data_num].gyro_z = 0;
			g_sens_data[new_data_num].mag_x = 0;
			g_sens_data[new_data_num].mag_y = 0;
			g_sens_data[new_data_num].mag_z = 0;
			g_sens_data_sum_cnt[new_data_num] = 0;

			uint8_t old_data_num = g_sens_data_num;
			g_sens_data_num = new_data_num; //           
			// ( -    ,   )

			//     -  
			int16_t avg_x = g_sens_data[old_data_num].acc_x / g_sens_data_sum_cnt[old_data_num];
			int16_t avg_y = g_sens_data[old_data_num].acc_y / g_sens_data_sum_cnt[old_data_num];
			int16_t avg_z = g_sens_data[old_data_num].acc_z / g_sens_data_sum_cnt[old_data_num];

			//      
			int16_t dx = avg_x - prev_avg_x;
			int16_t dy = avg_y - prev_avg_y;
			int16_t dz = avg_z - prev_avg_z;
			prev_avg_x = avg_x;
			prev_avg_y = avg_y;
			prev_avg_z = avg_z;

			//     
			if ((abs_i16(dx) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dy) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dz) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE))
			{
				//    
				raw[RAW_ACC][low_motion_cnt].x = avg_x;
				raw[RAW_ACC][low_motion_cnt].y = avg_y;
				raw[RAW_ACC][low_motion_cnt].z = avg_z;
				raw[RAW_GYRO][low_motion_cnt].x = g_sens_data[old_data_num].gyro_x / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_GYRO][low_motion_cnt].y = g_sens_data[old_data_num].gyro_y / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_GYRO][low_motion_cnt].z = g_sens_data[old_data_num].gyro_z / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_MAG][low_motion_cnt].x = g_sens_data[old_data_num].mag_x / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_MAG][low_motion_cnt].y = g_sens_data[old_data_num].mag_y / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_MAG][low_motion_cnt].z = g_sens_data[old_data_num].mag_z / g_sens_data_sum_cnt[old_data_num];

				low_motion_cnt++;

				//   
				beep();

				//     2   ,     -   
				//  -  
				//      
				delay_ms(2000);
			}
		}
	}
. . .
}


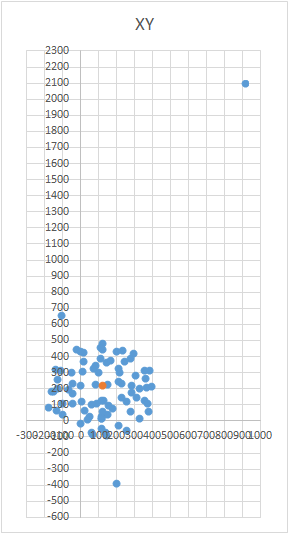
要在图表上显示球，您需要根据特定方案扭曲带有传感器的设备。为此，地球仪非常适合，因为它具有标记。您可能会认为您需要在全球范围内进行雕刻。但是事实并非如此。
错误的结果示例


有必要将传感器雕刻在地球的整个表面上，而不是在一个子午线上。假设我们在子午线上取了七个点（第一个点和最后一个点在北极和南极）。在子午线的每个点，我们都将您的设备连接到地球上，并仍然以一定的步长（例如30-35度）围绕设备的轴旋转设备。事实证明，如果绕其轴旋转12次，则总共可以在7个点上进行84次测量。



该方法的优点在于，一切都可以“在膝盖上”完成。定位精度没有特别的作用，您只需要按照方案扭转即可，以使外部影响图的矢量画出一个球。正确的外观看起来像这样-见图（中心标有标记）。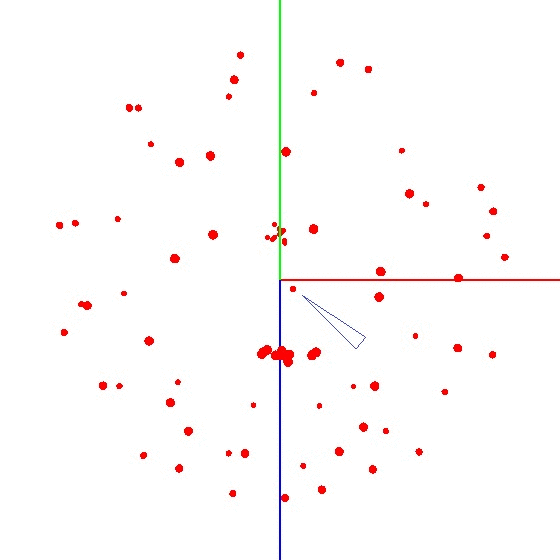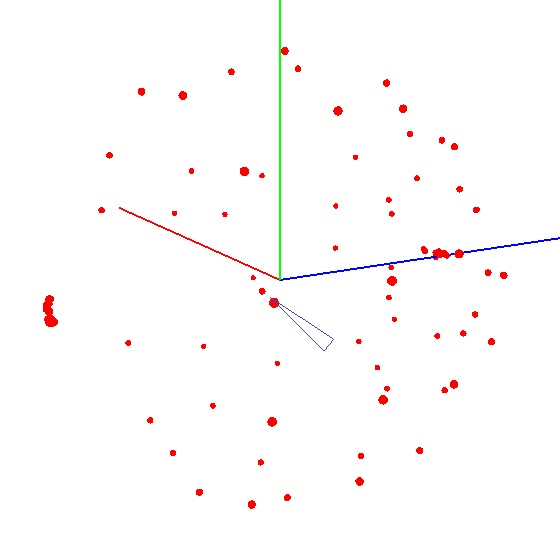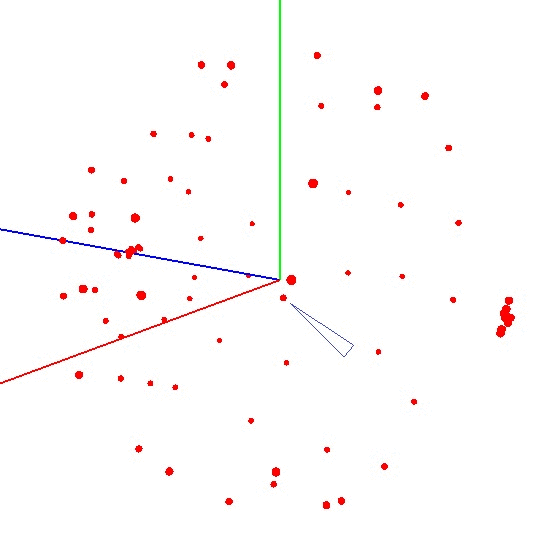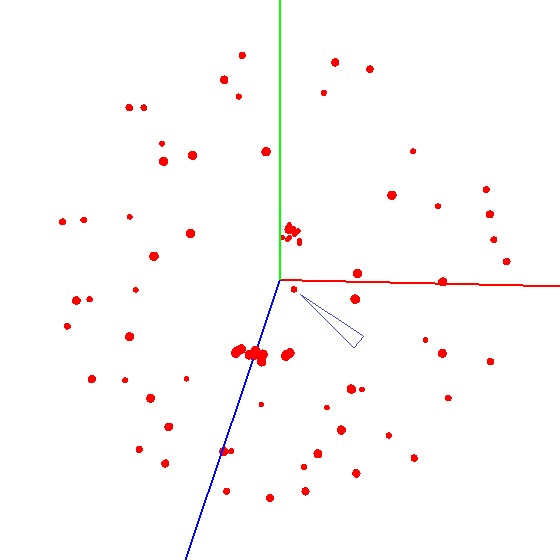



如何计算球的中心？


这是一项有趣的任务，它有多种解决方案。似乎要搜索中心，就可以对获得的点的坐标进行算术平均。但是，事实并非如此-这些点在球上的位置可能不均匀（请参见图）。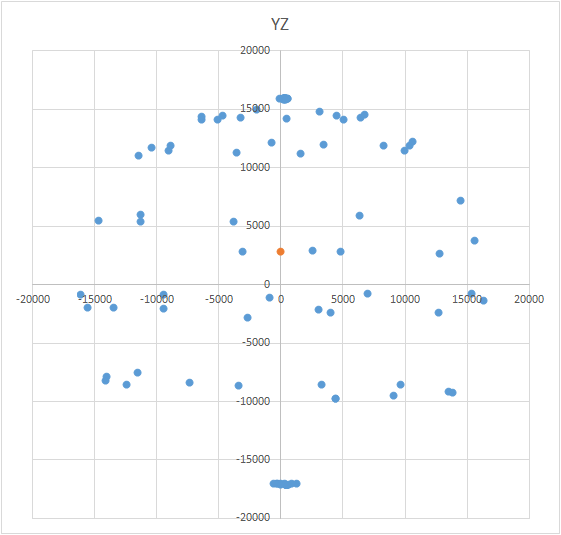



球的方程式如下：（X-A）2 +（Y-B）2 +（Z-C）2 = R 2，其中X，Y，Z是躺在球上的点的坐标。 A，B，C分别是x，y和z轴上的中心坐标。 R是球的半径。您可以建立一个方程式系统，并尝试使用某种方法更简单地求解该系统。或者，您也可以半身像找到中心（这就像一种逐次逼近的方法）。该方法的含义很简单：误差值（X-A）2 +（Y-B）2+（Z-C）2 -R 2应该趋于零。这意味着球体所有点的这些量之和也应趋于零。知道了这一点，我们可以选择值A，B和C，所有点的误差都将最小。搜索区域受球（条件立方体）的大小限制。也就是说，我们必须依次将球的中心放在立方体的所有点上并计算误差。误差最小的地方-中心。



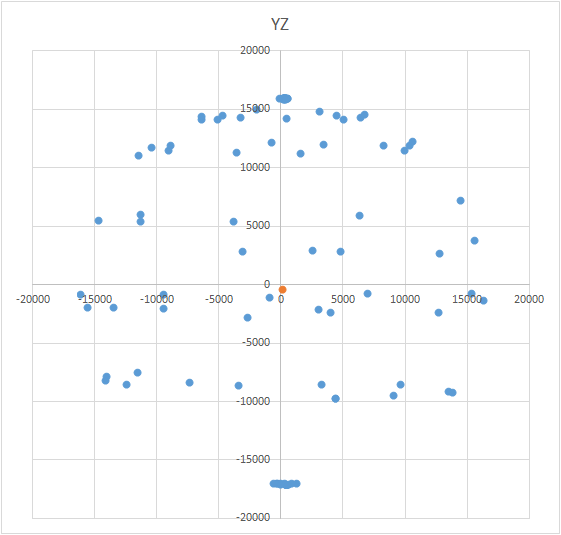作为R，我们需要采用外部影响矢量的理论值-对于加速度计，这是重力加速度，对于指南针-这是地球磁场的平均幅度，对于陀螺仪-地球的旋转速度。当然，在公式中应该有一维的值（传感器的常规单位或m / s 2，度/秒等）。转换为相应传感器的任意单位更为方便。
如何以传感器的标准单位计算某个值？
= * / ( — )
: 16- ±2g ?:
9,8 /2 * 65536 / (2g + 2g) = 9,8 /2 * 65536 / (2 * 9,8 /2 + 2 * 9,8 /2) = 16384 . . .

顺便说一句，如果您确切地知道球的半径，则只能通过其“楔形”计算中心。也就是说，在仅位于球的一部分表面上的点处。但这不是我们的情况。

如何加快寻找球心的速度？


有必要不在整个立方体（球的尺寸）中寻找中心，而是沿着直线寻找起点，该直线的起点是任意的，每个下一个点都靠近真实的中心，终点位于中心。假设我们从点（0; 0; 0）开始...我们总是以恒定的步长运动。因此，如果我们设想一组3x3x3立方体，其中每个面都等于步长，并且还想象当前位置是中间立方体，那么我们有9 + 8 + 9个选项可以放置下一个点。我们只需要在每个点上进行计算，即可计算出相邻26个点中的哪个点的误差会较小。如果事实证明该错误在当前点较小，而不是在相邻错误之一上，则表明该错误位于中心并且搜索结束。


怎么在代码中
Public Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
    x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
    y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
    z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
    get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function

. . .
A = 0
B = 0
C = 0

Do While True
   min_sigma = 0
    For ai = -1 To 1
        For bi = -1 To 1
            For ci = -1 To 1
                sigma = get_err(A + ai, B + bi, C + ci, 16384)
                If sigma < min_sigma Or min_sigma = 0 Then
                    ai_min = ai
                    bi_min = bi
                    ci_min = ci
                    min_sigma = sigma
                End If
            Next
        Next
    Next
    
    If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
        Exit Do
    End If
    
    A = A + ai_min
    B = B + bi_min
    C = C + ci_min
Loop
. . .



还有什么其他方法来加快对球中心的搜索？


需要以可变音调搜索。首先，我们大步寻找中心。我们找到了中心，我们减少了脚步，并从中开始进一步搜索。依此类推，直到获得必要精度的结果为止。
怎么在代码中
Public Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
    x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
    y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
    z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
    get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
step = 1000
Do While True
   min_sigma = 0
    For ai = -1 To 1
        For bi = -1 To 1
            For ci = -1 To 1
                sigma = get_err(A + ai * step, B + bi * step, C + ci * step, 16384)
                If sigma < min_sigma Or min_sigma = 0 Then
                    ai_min = ai
                    bi_min = bi
                    ci_min = ci
                    min_sigma = sigma
                End If
            Next
        Next
    Next
    If ai_min = 0 And bi_min = 0 And ci_min = 0 Then        
        step = step / 10
        If step < 0.01 Then
            Exit Do
        End If
    Else
    A = A + ai_min * step
    B = B + bi_min * step
    C = C + ci_min * step
    End If
Loop
. . .



关于测量误差


在测量过程中，由于某些原因，有时可能会导致测量结果离球的表面更远。或者可能有很多要点。或者，通常，测量结果可能不是球，而是“蛋”或“飞艇”。当然，在这种情况下，您需要重复所有测量，以找出可能的错误原因。例如，对于磁力计，它可以是桌子上的螺栓或钉子，而您正要在其上方进行测量。沿着子午线降低传感器的位置越低，金属越会影响结果。因此，有必要确定允许误差值的阈值。为了避免由于多个明显错误的点而导致无法重做测量，可以应用过滤器。过滤器的原理非常简单-首次计算中心后，请按每个点的误差等级对这些点进行排序。可以将一些误差最大的点简单地丢弃（例如10％）。然后，您需要重复搜索中心。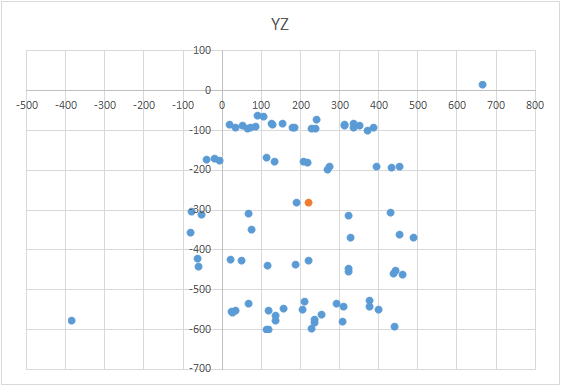


总


该方法具有很好的准确性。该方法允许您使用简单的简易方法（球，银行等）进行操作。它足够快地工作。简单的代码。许多传感器都有特殊的寄存器，您可以在其中写入找到的值，并且传感器会即时减去它。这样的寄存器通常在MPU9260中具有前缀“ TRIM”，在LSM303中具有“ OFFSET”。但是众所周知的LIS302DL没有这种寄存器。

如果喜欢，请不要忘了加一个加号。在注释中写下您的传感器校准方法。

Source: https://habr.com/ru/post/zh-CN384075/

More articles:


All Articles