👩🏻‍🤝‍👨🏼 🎒 ♈️ 压缩光或具有引力波的物体 👨‍❤️‍💋‍👨 🕎 👧🏽

你好，GT！今天，我们将讨论一种不寻常的光状态及其同样不寻常的应用。欢迎来到猫。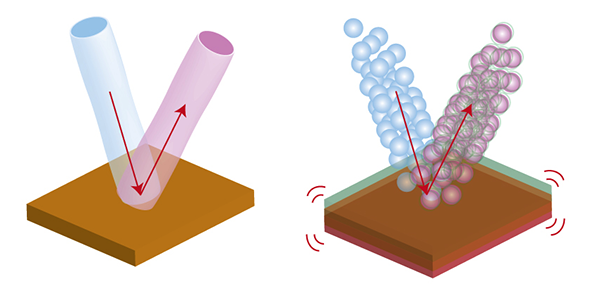

一名警察拦住了超速的海森堡。
“你甚至不知道你开车有多快？”
“不，但是我确切地知道我在哪里。”
（胡须轶事）

海森堡不确定性关系禁止同时测量粒子的坐标和速度（动量）。此外，没有人会费心去精确地测量其中一个量，但是第二个不确定性将变得更大。

通常，不确定性关系在物理学中非常普遍。例如，对于电磁波，同样的关系是成立的：它关系到其强度（=光子数）和相位：

由于存在这种不确定性，我们无法准确地测量波形所描述的正弦波，因为观察者将始终处于噪声雾中：

这可以在饼图中直观地显示，其中幅度对应于点的半径，相位-点的方向与X轴之间的角度，绿色表示不确定性：

在这种情况下，没有人什么麻烦事，以准确地确定任一振幅或相位。然后，误差圈将变成椭圆形，在一个方向上缩小，在另一个方向上拉伸：

这种情况称为压缩光，因为振幅或相位波动会沿轴之一压缩，从而减少了测量误差。第一种称为振幅压缩（椭圆在半径上延伸，您可以准确测量正弦波的最大值-最小值处的振幅）；第二个相位（沿半径为椭圆形，您可以测量正弦波零点处的相位）。

它为什么如此重要？

对于普通的光，我们无法准确地测量幅度或相位，而不是误差圈给我们的。这称为标准量子噪声水平。压缩光使您可以减少一个方向的误差，并在这种噪声水平下“潜水”。从某种意义上讲，我们可以[pathos_mode_on]进行比自然[pathos_mode_off]更准确的测量。

一个简单的例子。

每个光源每秒都会产生整数个光子。由于光的量子性质，它可以每秒变化，从而形成光子数量的分布（我在有关汉伯里·布朗和特维斯的故事中提到了这一点）。

光子的数量与光的强度相同。也就是说，强度有点“杂音”-从秒到秒变化。这是标准的量子噪声水平。

但是，如果光子数没有从第二个变化到第二个变化（右图），则强度严格恒定且没有任何噪声。这就是振幅被最大程度压缩的光。光子同时流动看起来像这样：

即，光子严格周期性地发射。如果违反了周期性，则光仍在某种程度上保持压缩状态。

为什么需要这个？

与其他异物不同，使用压缩光非常有前途。

电信。通过调制压缩变量（幅度（AM）或相位（FM），更通用的术语是正交）来传输信息，可以提高信噪比。可以构建仅将噪声添加到未经压缩且不携带有用信号的正交电路的放大器。

量子纠缠。在某些情况下，可以在光子的纠缠和光的压缩之间绘制平行线。例如，您可以混淆两束光束：一束振幅被压缩，第二束相位被压缩。

量子密码学。来自量子纠缠的茎和上图。在最简单的量子密码方案中，爱丽丝使用具有随机偏振的光子将信息传输给鲍勃。压缩方向可以起到压缩的作用：如果选择不正确，则拦截通信信道的攻击者将测量噪声而不是信号。

引力波探测器。对于此任务，您需要捕获巨大负载的最小波动。通常使用迈克尔逊干涉仪完成此操作。它的构建非常简单：一个激光器，两个镜子和一个半透明板：

激光从两个反射镜反射，两次反射发生干涉，并且在屏幕上形成干涉图案。如果其中一面镜子移动，那么图片也将移动。发生这种情况的原因是波的相位发生了变化：反射镜移开了-激光路径变得更长了，另外一个相位进入了-干涉带发生了移动。

由于干涉仪测量相位，因此其分辨率不能优于相位不确定度。对于常规激光器，它被限制为标准量子噪声水平。但是，如果我们用相位压缩的光源代替激光器，那么这个问题将消失，我们将能够以前所未有的精度测量距离。

如今，这是在最大的重力波探测器GEO600之一中完成的，并且很可能计划用于LISA空间探测器。顺便说一下，在GT用户中，有Shkaff，他只是这样做，并准备在评论中回答您的问题。

精确的相位测量。相位压缩光可用于使用相位对比法（现代生物学中的日常技术）进行测量。

如何产生？

创建压缩光并不是那么简单。为此，使用了非线性光学过程。用手指很难解释，但我举一个例子。

在某些晶体中，观察到一种称为Kerr非线性的效应-折射率对光强度的依赖性。让我们向这样的晶体发送激光脉冲。对于任何脉冲，其前端的强度都比中心的强度低-这意味着折射率将在脉冲的当前位置最强烈地变化。折射率的差异导致这样的事实，即中心和前沿的波相位变化不同。这些变化的总和导致了这样一个事实，即相位变得比平时更好，而强度则相反。你好，挤光:)。

如何检测？

压缩光也可以通过几种方法进行测量。

1.汉伯里·布朗-特维斯计划。

在有关汉伯里·布朗和特维斯的系列文章中，我说相关函数g ^（2）对应于光子数分布的宽度。光的振幅压缩意味着确定的光子数量比平时要好。因此，从广义上讲，单词g ^（2）小于^1-表示光被挤压。

2.天平探测器。它就像一个汉伯里·布朗-特维斯电路，但不是相关性，而是从两个二极管中减去或相加信号（根据我们的要求）：

半透明的镜子随机地透射或反射每个光子。这种随机性将额外的量子噪声（例如散粒噪声）引入信号中。这种噪声在两个二极管上具有不同的符号：如果反射了一个光子，则它将不会飞行；如果它飞了，它不会被反映出来。

如果我们从一个二极管中减去另一个二极管的信号，那么量子噪声将不会传播到任何地方。如果我们加起来？然后，噪声将消失，因为它具有不同的符号。（另一种解释：我们将光分为两部分，然后将它们折回-显然，这并没有增加额外的噪音。）

因此，减法会为我们添加标准量子能级的噪声，加法不会改变任何东西。如果所研究的光被振幅压缩（即“无噪声”），则相减将使其噪声更大，相加将使其保持不变。在加减之间切换，我们可以测量噪声水平，如果噪声水平不同，则可以观察到振幅被压缩的光。

加（红色）和减（蓝色）后的噪声看起来像这样。红色噪声要弱得多，并且对应于压缩光。

3.同质化。幅度压缩很容易测量，但是相位压缩又如何呢？如果可以“旋转”椭圆的方向（即光的相位），则来自相位压缩的光将变为振幅压缩。可以通过将光与参考波混合来旋转相位。这与接收机本地振荡器非常相似，只是在本地振荡器中参考波和研究波的频率不同，但是在本地振荡器中则没有（因此得名）。

即使在零差中，您也需要选择参考波的相位。在电子领域，这是通过移相器完成的，在光学领域是通过延迟线完成的（光到达的越晚，相位运行的越多）。混合在同一半透明的镜子上进行：

参考波来自下方。然后-相同的平衡探测器。

从有趣的

到目前为止，压缩光仅用于超精密干涉仪中。问题在于它非常脆弱。通过理想的振幅压缩光（光子通量严格是周期性的）的示例可以很容易地理解这一点：

在光的传播中，损耗是不可避免的，损耗总是随机的。这意味着光子将随机从流中消失：

如您所见，周期性几乎没有剩余。以及来自压缩。因此，压缩光很难长距离传输。

最后，让我们欣赏汉诺威附近的重力探测器GEO 600的方案：

压缩光的源在黄色背景上。它使用非线性光学过程，而不是Kerr非线性，而是辐射的二次谐波的生成。红色虚线是压缩光。右上方是肩长600米的迈克尔逊干涉仪；镜子悬挂在必须由重力波振荡的负载上。干涉仪的图像在右下角的光电二极管上获得。狐狸的

来源
。量子光学：入门 -牛津大学出版社，2006年。
感谢Shkaff的专业评论。免

图像：KDPV，1，2，3，4，5，6，7，8，9，10。