正如我们之前所写，在国立科技大学“ MISiS”举行了年度活动“圣诞节讲座”。在此活动的框架内，我们的领先科学家就其研究领域和主要成就进行了演讲。我们已经发表了D.V.的专家意见。霍尔伯格讲课。今天，我们要发表我们领先的科学家，项目经理的专家意见：“非晶铁磁微线的开发和应用，用于基于它们的新型传感器，复合材料和设备的创建”。乌索夫·尼古拉·亚历山德罗维奇教授。他的演讲“应用中的现代磁性：磁记录，生物医学，微电子学”这次活动于12月3日举行，给所有学生留下了生动的印象，许多研究人员在准备材料时都提到了他的脚步。我们的指导团队为该演讲编辑了一个非常不错的视频，顺便说一句，它的播放时间比其他人都长。我们不禁要求教授为我们写专家意见。与往常一样，尼古拉·亚历山德罗维奇（Nikolai Alexandrovich）非常负责任地完成了任务，两个月后，他向我们发送了材料。当然，这不是一种流行的科学形式，要理解它，将需要大学一级的物理知识。在他的专家看来，教授将谈论磁性纳米粒子及其现代技术应用。(CrO2), (Sn) (Sb).
, . .
磁性纳米粒子的集合在现代纳米技术中非常广泛地使用。足以提及磁性纳米粒子的重要应用，例如信息的超强磁记录，具有独特流变特性的磁流体，高矫顽力的永磁体等。最近，磁性纳米粒子的非常有前途的生物医学应用，例如磁共振成像，靶向药物递送和磁性热疗，深层清洁生物介质中的毒素和杂质等。 d。化学家，物理学家，工程师和技术人员多年来一直致力于各种磁性纳米粒子的集成，以寻求针对各种技术应用优化集成的物理化学性质。这项工作远未完成。首先，这是由于磁性现象本身很难研究这一事实。其次，使用纳米物体非常困难，只有借助先进的电子显微镜才能观察到纳米物体。铁磁物质具有特殊的磁序，这在普通物质中是不存在的。也就是说，在铁磁体的每个点上都有一个磁化矢量M®，其长度是恒定的，并且等于称为该物质的饱和磁化强度的物理量|M®|。 =女士饱和磁化强度是单位体积铁磁性物质中基本磁矩的数量，其行为与量子机械交换相互作用相关[1,2]。铁磁性的主要研究主题是根据所施加的磁场和其他因素，分析M®向量在铁磁性物体上的可能分布类型。事实证明，向量M®不能突然，突然改变，而只能在磁化体中从一点到另一点平滑旋转，保持其长度。因此，实际上，磁性是三维矢量场。请注意，我们生活在各种物理领域中。例如，我们周围及其周围的温度分布不均匀是三维标量温度场。该字段由单个函数T（r，t）描述，该函数不仅取决于点在空间r中的位置，而且取决于时间t。为了描述向量场，需要三个函数-该向量在笛卡尔坐标系的轴上的投影{Mx（r，t），My（r，t），Mz（r，t）}。磁性矢量的一个基本属性是该磁性矢量的长度的恒定性Mx2（r，t）+ My2（r，t）+ Mz2（r，t）= Ms2，这是由量子力学定律[ 1,2]。该关系是非线性的，因为它连接了数量的平方。因此，铁磁性的研究需要使用特殊的非线性数学，这比普通的数学分析要复杂得多。此外，任何磁化体都会在其内部和周围产生磁场分布H®，磁场本身会影响铁磁体中磁化的分布。当离开磁化体时，磁场H®在空间中缓慢减小，与〜1 / r3成比例，也就是说，它是远距离的。这意味着，即使足够远的磁化体部分也通过磁相互作用连接，也就是说，它们的行为是一致的。也就是说，它是远程的。这意味着，即使足够远的磁化体部分也通过磁相互作用连接，也就是说，它们的行为是一致的。也就是说，它是远程的。这意味着，即使足够远的磁化体部分也通过磁相互作用连接，也就是说，它们的行为是一致的。这两种情况-描述M®向量在空间中分布的方程式的非线性以及磁相互作用的远距离特性使铁磁材料的特性的理论分析极为复杂。尽管Landau和Lifshitz早就建立了现象学铁磁的基本方程，但在其1935年的著名著作中[3]，与强大的计算机模拟方法的发展有关，铁磁学理论的发展才出现在上世纪90年代。迄今为止，磁性纳米粒子仍然是铁磁性理论的中心对象之一，并且仍然是实验研究的重要领域。事实是，扩展的铁磁体具有很大的磁性自由度。的确在宏观上，M®向量可以以多种方式在空间中扩展。可以说这种现象是由于存在大量稳定的磁化分布，它们也可以很容易地相互转化。因此，扩展的铁磁体的特性难以控制，因为难以固定这种物体的磁性。然而，很明显，随着身体体积的减小，磁性自由度的数量急剧减小。实际上，量子力学交换相互作用仅允许空间中的向量M？发生相当平滑的变化，其特征长度超过所谓的交换长度Lex。在良好的铁磁体中，例如铁，钴，镍及其合金，交换长度约为20至30纳米。如果纳米颗粒D的特征尺寸小于或等于交换长度D ＜Lex的量级，则这种颗粒内的磁化矢量的逆转在能量上是不利的。说一个域的特征尺寸Dc更为严格[4]，在所谓的软磁铁磁体中，它接近交换长度Dc〜Lex。尺寸小于单个畴直径D <Dc的粒子被均匀磁化，也就是说，它们的磁化矢量与坐标M = const无关。具有最简单磁性结构的此类粒子称为单畴。单畴粒子是几乎不可能消磁的小型永久性天然磁体。如果颗粒尺寸超过单个畴的尺寸，D> Dc，则在这种颗粒中会形成通常为涡旋型的不均匀磁化分布。通常为涡流型。通常为涡流型。图 1.使用三维计算机仿真获得直径D = 36 nm的球形钴纳米颗粒（左）中的均匀磁化状态和直径D = 56 nm的同一纳米颗粒中的不均匀涡旋状态（右）。
在图。图1显示了通过现代数值方法[5]在不同直径的球形钴纳米颗粒中计算出的磁化强度的均匀分布和涡旋分布。这些图中磁化矢量的三维分布在这些图中由固定长度的箭头表示。为了确定球形钴纳米粒子的单畴直径，需要计算这些状态的能图，如图1所示。2。图 2.取决于纳米粒子的半径的纳米粒子的稳定磁态的示意能量图。
从图可以看出。如图2所示，粒子的均匀磁化状态的总比能（黑线）不取决于粒子的半径，而涡旋状态的总比能（红色曲线）随着半径的增加而迅速减小。这些曲线的交点确定粒子的单个域的半径ac = Dc / 2。如果粒子半径r <ac，则均匀态的总能量最低，而在一定半径范围内的涡旋态可以亚稳态存在，即是稳定的，但具有更多的能量。如果r> ac，则涡旋态的能量最低。在这种情况下，均匀半径可以在半径ac <r <Rc的范围内作为亚稳态存在，其中Rc是均匀半径的稳定半径。对于大多数技术应用程序，使用单个域纳米粒子的集合是很方便的，其性质可以相对准确地预测和控制。在所有情况下，单畴纳米粒子都会保留其完整的磁矩，而处于涡旋状态的粒子的平均磁矩可能很小，因为在此状态下的磁矢量会自行闭合。对于处于涡旋状态的粒子，磁矩的平均值基本上取决于作用在粒子上的外部磁场的大小。从图中图。图2显示，如果该集合体在单个域的半径附近具有纳米粒子的大小分散，那么实际上这样的集合体是具有不同属性，单个域而不是单个域的粒子的不受控制的混合物。如果你仍然考虑由于单个域的半径值取决于粒子的形状（球形，细长或扁球形），因此实验情况变得非常混乱。我们看到，磁性纳米粒子的集合是一个相当复杂的物理系统，其性质由许多不同的因素决定。在大多数情况下（尽管并非总是如此），集成体由化学成分相同的纳米颗粒组成。因此，该集合体的粒子可以用一组材料磁参数来表征，即饱和磁化强度Ms，磁各向异性的类型以及磁各向异性常数K的值。磁各向异性确定了空间中相对于晶体对称轴的显着方向（所谓的光轴）。在没有外部磁场的情况下，粒子磁化矢量会自发地沿着磁性晶体的光轴定向。但是仅指定磁参数完全不足以完整表征纳米颗粒的集合。有必要知道纳米粒子的大小和形状的分布。纳米粒子的各向异性光轴的数量和方向（定向或非定向集合体）；纳米粒子中心在空间中的分布。例如，纳米粒子的中心可以周期性地定位，形成一定的空间晶格，或占据随机位置，粒子之间具有一些平均距离。或占据随机位置，粒子之间有一些平均距离。或占据随机位置，粒子之间有一些平均距离。请注意，通常在实际实验中，研究的是相当密集的粒子集合，其性质与稀有集合的性质明显不同。致密粒子集合体的特性的理论研究受到该集合体粒子之间的磁偶极子相互作用的远距离影响。因此，对于有Np个粒子的集合体，必须考虑粒子的Np2对相互作用，从而随着集合体中粒子数的增加，计算复杂度迅速增加。此外，集成体所处的环境对集成体的性能具有重要影响。我们应该区分粘度相对较低的介质和整体介质（例如固体基质），该介质在整体磁场中无法旋转，而介质在外部磁场或相邻粒子的磁偶极相互作用的影响下可以整体旋转。最后，环境温度会显着影响足够小尺寸的颗粒（超顺磁性纳米颗粒）的性能。如果介质的温度超过阻止纳米粒子磁矩的所谓温度，则单个粒子磁矩的温度波动会大大降低集合体的平均磁矩。让我们继续进行技术应用。具有单轴磁各向异性的单畴磁性纳米粒子的磁矩在空间上具有两个不同的方向。在足够低的温度（例如室温）下，粒子可以无限期地保留在这两种磁性状态的每一个中。因此，它保留了获取的磁性状态的存储器，这意味着它可以在足够长的时间内无损失地存储信息。如果我们任意地将值“ 0”分配给粒子向上的磁矩方向，将值“ 1”分配给粒子向下的磁矩方向，如图5所示。剩下3个，则可以将零和一的序列中的一些二进制文本存储在一组特殊的纳米粒子磁性状态下。当前，在磁记录过程中，一位信息没有记录在一个信息上，并收集20-40个紧密排列的磁性纳米粒子。向“一位-一个粒子”的原则过渡到记录将大大增加信息的磁记录密度。然而，为实现这一有趣的想法必须克服的基本技术难题是显而易见的。首先，该集合体的颗粒应该基本相同并且周期性地位于该平面中，其晶格周期为纳米颗粒大小的量级。更令人惊讶的是，化学家们最近学会了使用自组装过程，即在化学反应过程中团聚颗粒的生长过程中对它们进行自我组织，从而创建了磁性纳米颗粒的相似的，几乎理想的周期性结构[6]（参见右图3）。图 3.对具有两种磁性状态的单个磁性纳米粒子（左）进行超密集磁记录信息的原理以及通过化学自组装方法获得的FePt磁性纳米粒子的周期性结构。
但是，为了实现信息的密集记录的思想，除了实现整体的正确的几何结构之外，还必须确保合成的纳米粒子的磁各向异性常数的值足够大。原则上，具有规则晶体结构的FePt颗粒（其中铁原子的平面与铂原子的平面规则地交替）具有创纪录的高磁各向异性常数值，K = 5 * 107 erg / cm3，[7]这样可以在保持颗粒磁性状态的过程中保持稳定时间和直径足够小的粒子。实际上，要在两个易于磁化的方向之间传递粒子的磁矩，有必要克服高度的能垒
其中V是纳米粒子的体积。为了在足够长的时间（10年）内防止由于热波动引起的自发扭矩传递，必须满足严格条件KV>（50-70）kBT，[7]其中T是环境温度，kB是玻尔兹曼常数。随着粒径的减小，能垒迅速下降，但是颗粒的磁各向异性常数的大值允许人们保持对于纳米尺寸的颗粒的所示不等式。不幸的是，当铁和铂原子在晶格中占据任意位置时，通过自组装生长的FePt颗粒[6]处于取向错误的磁性状态。并且在这种情况下，物质的磁各向异性常数很小，比指定的护照值小几个数量级。尽管使用退火和其他方法付出了巨大的努力将FePt颗粒转移到有序的磁性状态，但这一基本问题尚未解决。通常，小磁性粒子的温度波动对其磁矩的磁态影响的问题被称为超顺磁极限[7]，并且仍在等待解决。因此，颗粒的磁矩的温度波动导致在创建超密集信息记录的磁性载体方面的显着困难。同时，它们被证明对于开发磁性纳米颗粒有趣的生物医学应用之一，即用于治疗危险性肿瘤疾病的磁性高温治疗方法非常有用。实验证明[8]，将受影响器官的温度在约42°C保持20至30分钟。导致癌细胞坏死，比正常组织更易受高温的影响。许多铁磁材料能够吸收外部交变磁场的能量，从而加热周围的组织。但是，磁性纳米颗粒对于磁性热疗具有明显的优势，因为：a）超顺磁性纳米粒子的集合体能够提供非常大的比能量吸收值，约为每克物质1 kW； b）由于纳米粒子尺寸小，可以深入生物材料中； c）氧化铁纳米颗粒对生物体无毒或微毒，d）它们具有短时间从体内清除的能力。如上所述，磁性纳米粒子是一种非常强的天然磁体，因为即使在室温下，即使是软磁性氧化铁粒子，其磁化反转的特征场也非常大，Hc（0）〜2K / Ms〜400E。但是，重要的是，能量势阱分离的势垒的减小随着颗粒体积V〜R3的减小而减小，并且可以与特征热能kBT进行比较。在这种情况下，由于磁矩的热波动，粒子失去了其平均恒定磁化强度，成为超顺磁性。磁矩在给定势阱中的特征停留时间（尼尔弛豫时间）估计为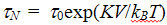
，其中常数
[9]。弛豫时间随着粒径的减小而迅速呈指数下降。只要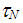
它等于或小于磁矩的特征测量时间
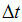，粒子的时间平均磁矩就等于零。但是超顺磁性现象具有积极的一面。热波动使势阱中粒子的磁矩摆动，有效地降低了能垒，并显着降低了粒子磁化反转场的大小。因此，超顺磁性粒子的集合体能够在中等振幅H0〜100-200 Oe的外部可变磁场中磁化，这对于磁热疗极为重要，因为这简化了产生交变磁场的条件并降低了必要设备的成本。从热力学[1,2]中知道，交变磁场的能量吸收强度与磁性纳米粒子集合的磁滞回线的面积成正比。在我们的小组中，对各种类型的磁性纳米粒子稀疏集合的低频磁滞回线进行了理论计算[10，11]，并通过原始方法进行了相应的实验测量[12，13]。理论计算表明，磁滞回线对交变磁场频率的依赖性很大，如图2所示。4。图 4.磁性纳米粒子能够有效地远程吸收交变外部磁场的能量，从而加热环境。但是，这种能力在很大程度上取决于暴露的频率以及许多其他物理参数。
理论分析表明，[10]（参见图5）表明，如果将粒子固定地固定在周围的非磁性介质中，则超顺磁性系的磁滞回线也非常取决于平均粒径。尽管同时也证明了比能吸收对许多其他因素的显着依赖性，例如在磁性纳米粒子的密集集合中磁偶极子相互作用的影响，但这一重要事实在许多近期的实验中得到了证实[12，13]。图 5.钴纳米粒子（f = 500 kHz，H = 200 Oe）和磁铁矿（f = 400 kHz，H = 120 Oe）的稀疏集合所产生的交变磁场能量的比吸收的理论计算[]，具体取决于粒径。
磁热疗是局部和远程暴露，显然没有化学疗法或放射疗法的严重副作用[8]。磁热疗的成功发展似乎将取决于几个问题的成功解决。首先，有必要改进在中等振幅的交变磁场中具有足够大的比能吸收的纳米颗粒集合体的制备方法。这将减少纳米颗粒的剂量，足以实现积极的治疗效果。理想地，将希望学习如何局部地局部加热少量组织，以便在早期抑制小的，非常危险的肿瘤。此外，必须确保产生足够振幅的交变磁场，在人体的给定区域具有必要的空间分布，以合理的能源成本，保证了防触电的安全性，成本适中。最后，有必要学习如何控制效果本身，选择磁场的幅度和频率，纳米粒子的磁性和几何参数，暴露的时间和频率，并考虑到介质的电动力学和热学参数。还非常希望控制受影响区域中温度的时空分布。当前，这些问题成为各种配置文件研究人员关注的焦点。考虑到介质的电动力学和热学参数，纳米粒子的磁性和几何参数，曝光时间和频率。还非常希望控制受影响区域中温度的时空分布。当前，这些问题成为各种配置文件研究人员关注的焦点。考虑到介质的电动力学和热学参数，纳米粒子的磁性和几何参数，曝光时间和频率。还非常希望控制受影响区域中温度的时空分布。当前，这些问题成为各种配置文件研究人员关注的焦点。[1] . . , (, , 1985).
[2] .. , (, , 1972).
[3] L. Landau and E. Lifshitz, Phys. Z. Sowjetunion 8, 153 (1935).
[4] W.F. Brown, Jr., Micromagnetics (Wiley-Interscience, New York — London, 1963)
[5] N.A. Usov and J.W. Tucker. Material Science Forum 373-376, 429 (2001).
[6] S. Sun, C. B. Murray, D. Weller, L. Folks, and A. Moser, Science 287, 1989 (2000).
[7] D. Weller and A. Moser, IEEE Trans. Magn. 35, 4423 (1999).
[8] Q.A. Pankhurst, N.K.T. Thanh, S.K. Jones, J. Dobson, J. Phys. D: Appl. Phys. 42, 224001 (2009).
[9] W.F. Brown, Jr., Phys. Rev. 130, 1677 (1963).
[10] N. A. Usov, J. Appl. Phys. 107, 123909 (2010).
[11] N.A. Usov, B.Ya. Liubimov, J. Appl. Phys. 112, 023901 (2012).
[12] S. A. Gudoshnikov, B. Ya. Liubimov, and N. A. Usov, AIP Advances 2, 012143 (2012)
[13] S.A. Gudoshnikov, B.Ya. Liubimov, A.V. Popova, N.A. Usov. J. Magn. Magn. Mater. 324, 3690 (2012)