« », : , , . . . .
, : , , , , … , , , « » .
, «» «» , :

- , , . , , , ) .
, .
, , —
. , , . , - .
«» . , , .
, :
? , . :
« . , . , , .»
. ( )

, «dt», «» (.. «dy») «x».
«x» (.. «dx») «y».
— « = * ». «dt» ( , , ).
. . , , , :

, . - .
, .. «x» «y» , , - , .
html<html>
<body>
<canvas height='300' width='300' id='cnv' style="border: 1px solid black"></canvas>
<canvas height='300' width='200' id='cnv2' style="border: 1px solid black"></canvas>
<script>
var cnv = document.getElementById("cnv");
var cx = cnv.getContext('2d');
var cnv2 = document.getElementById("cnv2");
var cx2 = cnv2.getContext('2d');
var h = parseInt(cnv.getAttribute("height"));
var w = parseInt(cnv.getAttribute("width"));
var h2 = parseInt(cnv2.getAttribute("height"));
var w2 = parseInt(cnv2.getAttribute("width"));
var id = cx.createImageData(w, h);
var id2 = cx2.createImageData(w2, h);
var rd = Math.round;
var x = 0, y = 1, x1, y1;
var dt = 0.0001;
var t=0;
i=1000000; while (i--) {
dx = -y;
dy = x;
x1 = x + dx*dt;
y1 = y + dy*dt;
t = t + dt;
x = x1; y = y1;
// draw (x, y)
drawOn(id, rd(100*x + 150), rd(100*y + 150), w, h, 0, 0, 0);
// draw x(t), y(t)
drawOn(id2, rd(10*t), rd(100*y + 150), w2, h2, 255, 0, 0);
drawOn(id2, rd(10*t), rd(100*x + 150), w2, h2, 0, 0, 255);
}
drawHorizLine(id, 0, w, h/2, w, h);
drawHorizLine(id2, 0, w2, h2/2, w2, h2);
cx.putImageData(id, 0, 0);
cx2.putImageData(id2, 0, 0);
function drawOn(id, x, y, w, h, red, green, blue) {
if (x < w && y < h && x >=0 && y >=0) {
var idx = 4*(x + y*w);
id.data[idx] = red;
id.data[idx+1] = green;
id.data[idx+2] = blue;
id.data[idx+3] = 255;
}
}
function drawHorizLine(id, xFrom, xTo, y, w, h) {
for (var x = xFrom; x < xTo; x++) {
drawOn(id, x, y, w, h, 0, 0, 0);
}
}
</script>
</body>
</html>
— , .. «» «» ( ).
, — , — … . …
«x» «y» ( ) , /2
 , .
, .. 3- . , , , .
, ( ). ( ).
«E» ( ) «B» ( )

( « », )
, , .. . . -. — «E», «B» «t», , «J» , , .
, «», «B», , . .
— «» «B», .. «» . - . , , .
, ,
, , /2.
, . , , (=), , … .. ( ) , .
… :

… ? , , !
? . . ? . ?
- … ? . « , ». «», . , ? , 300 , - ?
:
www.sciforums.com/threads/luminiferous-ether.57402Hi BillyT,
From my understanding Vern is correct. Your citation of Maxwell's equation is a good idea, but you are incomplete. In free space you have no currents and no charges so Maxwell's 4 equations simplify down to 2 equations (considering a single spatial dimension):
dE/dx = -dB/dt
dE/dt = -c2 dB/dx
So when the temporal derivative of one is maximal the spatial derivative of the other is minimal (maximally negative). If you consider a simple single-frequency sinusoidal plane wave you find that this happens for E and B in phase. In the above equations:
E = Emax cos(kx-wt)
B = Bmax cos(kx-wt)
, , . .
? , .? !
dE/dx — .
«» . ,
3 ( ).
, . , .
, , «». , , , .

, , .
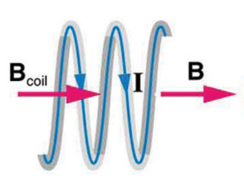
, ( ), , — .
?…

, , .. , . , .. , .
… /2 .? … - . , - ().
?,
- , .. .… ? ?