到目前为止，在神经系统模拟器的研究中，我们只研究其工作得到充分研究的方面。但是，神经系统建模的复杂性以及尚未创建人工智能的原因是，对神经细胞的工作原理缺乏全面的了解。详细描述了整个神经细胞和神经系统中发生的许多过程，但是尚无明确的算法可将它们的工作转移到模型或计算机程序中。神经元算法的简单思想帮助解决了这个问题。内容1. 神经系统模拟器。第1部分。简单的加法器。2 .神经系统的模拟器。第2部分。调制的神经元。3。神经系统模拟器。第3部分。联想神经元4. 记忆，记忆巩固和祖母的神经元5. 情绪建模或新奇的电子感觉6. 小脑令人惊奇7. 结构和开始的大脑设置我喜欢用杰夫·霍金斯（Jeff Hawkins）的著作《智力》（On Intelligence）中的难题来拟定大脑工作理论的类比。编译此拼图时，我们缺少某些要素和其他拼图中的某些要素，但是我们拥有大量有关神经系统和大脑的数据，这意味着我们有一个几乎是组装好的拼图，因此我们可以大致想象整个图片，并使用我们的想象力找出了缺失的要素。我的目标是创建神经系统的逻辑模型，可以说是为未完成的难题描绘的草图的创建，此外，它应该对应并且不矛盾难题的所有可用元素，并且在逻辑上是完整的。为了填补这些空白，创建了一些理论基础，这似乎对某些人有争议。但是对于现阶段的模型，主要的是它允许您模拟神经系统中发生的内部和外部观察到的现象。在获得的模型的框架内，可以解释许多现象，例如记忆和记忆巩固，情绪，神经元的特化等等。在第二部分中，我们发现I.P.院士建立了三种反射活动。巴甫洛夫。如果关于成瘾和致敏的生物学机制一切都非常清楚，那么条件反射的形成并不像看起来那样简单。事实是，广泛研究和描述了该机制的外部表现，没有解释在细胞水平如何发生。
例如，我们知道，当两个神经中枢的活动与时间结合在一起时，它们之间就会形成一个反射弧。即随后，一旦激活一个神经中枢，就会将兴奋转移到另一个神经中枢。如果我们将这种反射弧形象地划分为多个段，并将这些段视为单独的元素。可以说，当形成条件反射的反射弧时，在每个段中发生方向切换。每个节段选择一个特定的方向，神经节段被激活时就会发生神经兴奋的传递。当然，值得注意的是，该方向并未明确定义细分，但可以与某些值相关。您甚至可以谈论在某个方向上增强传输，而在其他方向上减弱。
当通过重复重复来增强反射时，我们可以谈论在每个段的方向上细化和增强传输。这个概念得出的结论是，如果我们将整个皮层划分为相似的段，我们将在每个方向上观察到一定的方向，而这些方向具有不同的精度和强度。每个段将通过条件反射或非条件反射的某些反射弧的一部分干燥。据推测，可以改进或改变学习过程中的这种方向。
如果我们转向神经范式，那么它就不会在方向上提供方向。我们有一个膜和树突来接收信号和一个轴突，在时空求和后，信号沿着轴突进一步传给其他细胞，也就是说，信号沿着轴突朝一个方向传到其末端。但是与此同时，我们仍然观察到大脑中定向兴奋性分布的形成，以及条件反射的形成。神经元范式, . . -, , .. . -, - -. -, . , — , . , . , , . .
如果我们不是将单个单元视为方向切换的功能单元，而是将一小部分单元视为单元，则可以看到单元及其过程紧密地交织在一起，并且方向不同。这提供了定向通信的元素，在各个方向上都有许多输入和输出。
神经元的形状归因于进化变化。细胞的形状是在仅执行最简单的神经活动功能的神经系统中形成的。当地球上的生命发展需要在神经系统的一系列功能中增加捕获反射的形成时，进化就不会遵循细胞重组的路径，而是细胞数量的增加和过程的紧密交织。因此，在神经元突触强度的变化中，方向转换的属性分布在神经元组中。关联神经元是建模中的功能单元，因此在生物学上是类似物，因为它是一组神经元，将针对这些神经元表达方向转换现象。我们发现激励传播的方向对我们很重要，但是对于每个功能元件如何确定该方向。众所周知，激发趋向于扩散到另一个激发源，激发的更强更广泛的焦点吸引了更弱的激发源（I. Pavlov的结论）。即如果功能元件受到刺激，则它必须以某种方式确定随后将形成并保留在其结构中的方向。在建模工作中，我从神经细胞的电磁相互作用的概念开始，这一思想为大脑的许多难题提供了答案，并提供了解释神经系统许多方面的理论和模型。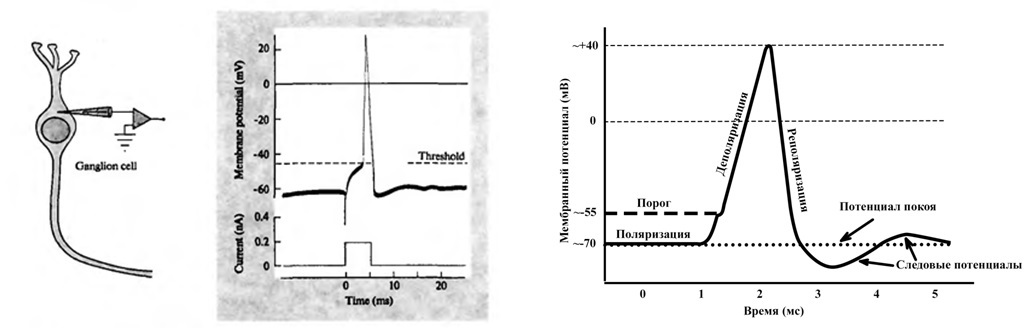
整个神经系统中的神经冲动具有相同的形状，并且与之类似，缔合性神经元具有电荷的特性，表征了功能单元膜表面总电荷的变化。即给出了称为电荷的某种特性的某种变化定律。
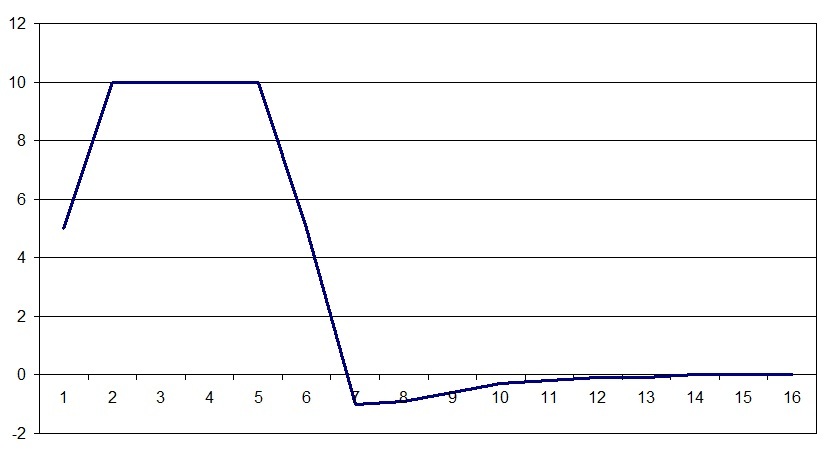因此在程序中设置了定律，水平标度是时间（以百分之一秒为单位），垂直电荷是相对单位。它与高峰计划有所不同，因为最大值的时间较长。这是由于以下事实：在激发过程中，尖峰的值是在神经组织中的某一点确定的，电荷图是电荷在一个细胞或一组细胞的所有表面上的反射。而且，神经组织的其余状态在电荷标度上取为零。应当注意，电荷变化定律也反映了痕量电势，以前认为这是由膜分离的电荷一定振荡或排列的结果，但是电荷的行为对于模型非常重要。
上图显示了关联神经元的示意图。来自直接作用突触（X1，X2，X3 ... Xn）的信号进入加法器（a）。并且如果结果量超过某个阈值（b），则将激活神经元。当神经元被激活时，其电荷将根据既定法则（c）开始变化。有关这些更改和元素本身位置的信息将对整个系统可用。接下来，在某个时间点，用于确定激励的优选传播方向的矢量（g）的机制开始。这是通过获取所有活动神经元的某个平均电荷位置来实现的，即质心，以空间中的点为特征。该点称为模式的点，因为对于每种神经元在计算的时间点，对于活性细胞的每种组合及其电荷状态，此点的位置将有所不同。简而言之，神经元的电荷会影响首选激发传播方向矢量的确定，正电荷吸引激发，负电荷排斥。为了确定优选激发传播的矢量，选择了一个规则：
其中r是矢量，其起点在要确定矢量的神经元的中心，而终点在第n个神经元的中心。凭经验选择电荷变化的规律和规律，以模拟条件反射的形成。本文中有更多详细信息。
接收到激励的最佳传播方向（T）的向量后，计算突触（Y1，Y2，Y3 ... Yn）。每个突触的特征是突触载体（S），其起始点位于神经元的中心，末端与信号要传输到的目标神经元的中心相连。突触的主要参数是其强度F，力的值限制在某个框架内，例如，感应突触的值可以从0到10。想象一下，向量T在其周围形成一个圆锥体，其顶部位于神经元的中心，并且底面垂直于向量T，如果突触矢量落入该圆锥体限定的区域，则突触的值将增加一定值。相应地，如果突触矢量在圆锥区域之外，则突触力会减小，但力值不会超出已建立的最大值和最小值。围绕矢量T的视锥区域的特征在于给定视锥顶点处的角度，该角度称为焦点。焦点越小，将更准确地确定神经元中兴奋传递的方向。如前所述，当身体重复相同的条件反射时，它会被完善。因此，为模型选择了以下焦点改变方法，在计算向量T时将其与先前值进行比较，如果向量变化不大，则焦点会减少一定值，但是如果向量发生了很大变化，则焦点会返回其最大值。随着相同条件的重复重复，这导致焦点逐渐减小。这是非常重要的一点，这是每次激活后突触强度会改变多少。这由神经可塑性参数P决定。突触力新值的公式为：Fnew = Fold + I×P×（Fmax-Fmin）;Fmin≥Fnew≥Fmax;其中P是神经可塑性（0≥P≥1）;I是确定突触矢量是在突触强度增加的区域（I = 1）还是在突触强度减小的区域（I = -1）的参数；折叠-先前的突触强度值；Fmin-突触力的最小值；Fmax-突触力的最大值。生物学中的神经可塑性表征了神经元在外部条件的影响下如何可延展其结构的变化。大脑的不同区域以其自身的可塑性程度为特征，并且还可以根据某些因素而变化。
这个例子让我们了解了基于联想神经元的条件反射是如何形成的。白色神经元形成无条件反射的反射弧，标题为“ R”，答案为“ 1”。这些神经元不会改变其突触的强度值。蓝色神经元最初并不参与任何反射动作，它们似乎充满了神经系统的其余空间，并且它们通过突触意外地连接在一起。因此，如果我们激活一个与“ Q”受体相关的神经元，那么兴奋的某个焦点就会显现出来，具有随机的传播特性，与自身循环后，它会在一段时间后消失，而不会产生任何答案。如果我们将无条件反射与标题“ R”和“ Q”受体的激活在大约相同的时间间隔结合在一起，然后将形成条件反射的反射弧。并且仅激活“ Q”受体就会导致答案“ 1”。为了使模型更清晰和最优化，我们使用了动态创建神经元的方法，该方法模拟了具有随机连接元素的神经系统的填充空间。在这里，没有模拟新神经元的某些生长或新连接，所有变化仅发生在突触的强度上，只是未显示以前未参与任何反射动作的神经元。
以下示例显示了在相同条件下以绝对可塑性（P = 1）激活不同中心时的激励行为。
当可塑性为绝对（P = 1）时，在两个激发中心的影响下，激发的传播方向发生变化：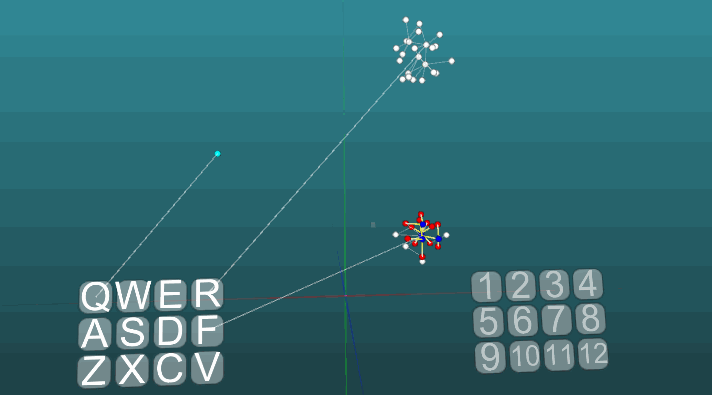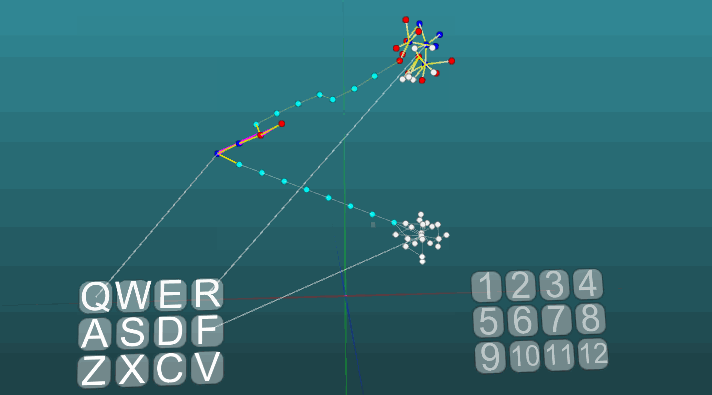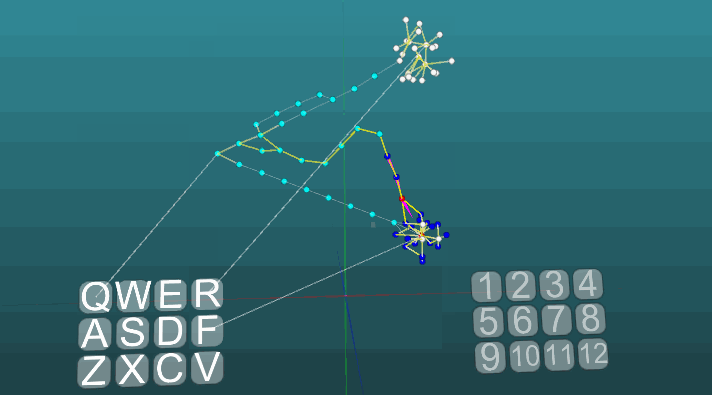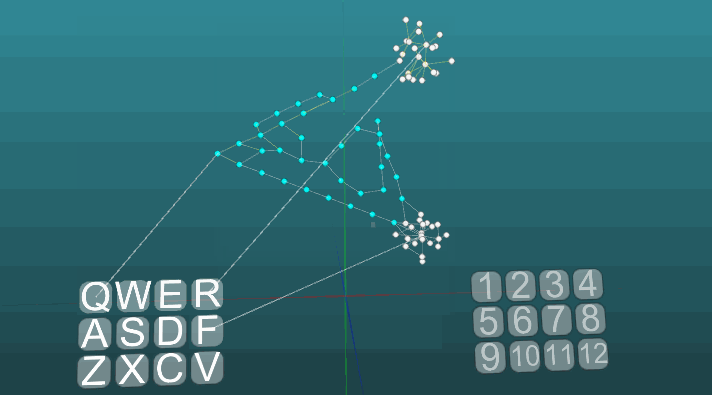
在低可塑性（P = 0.1）时：
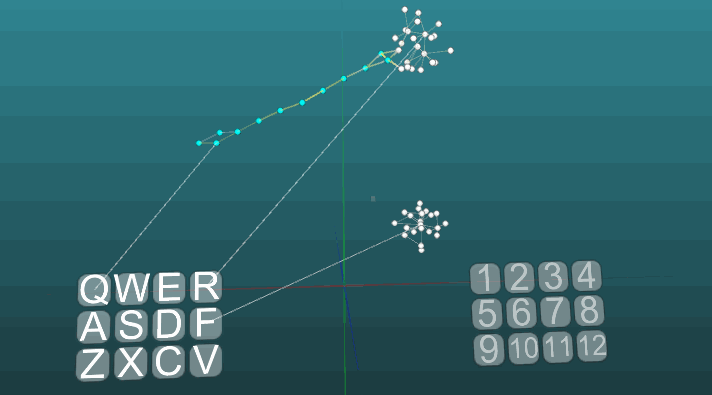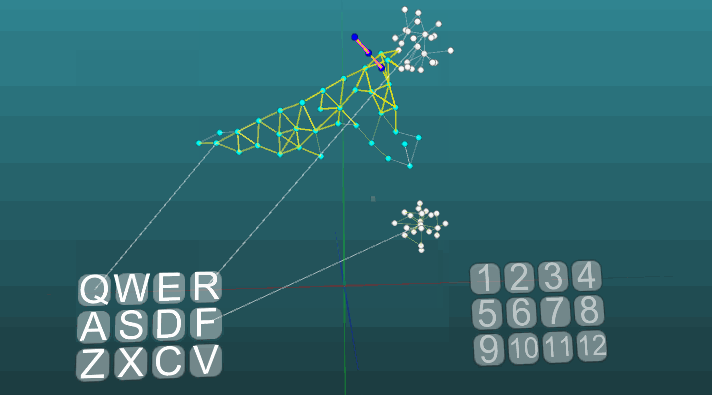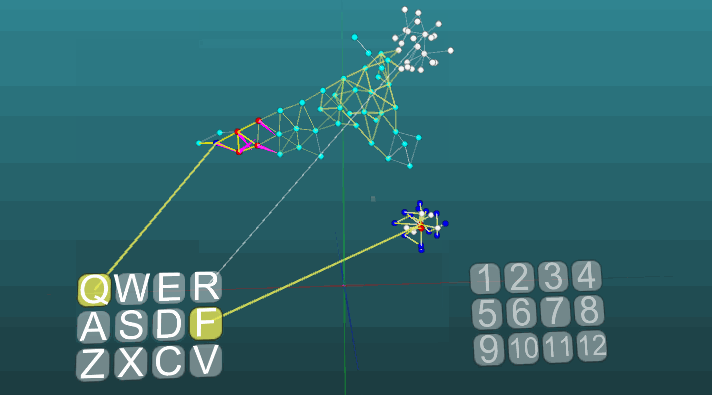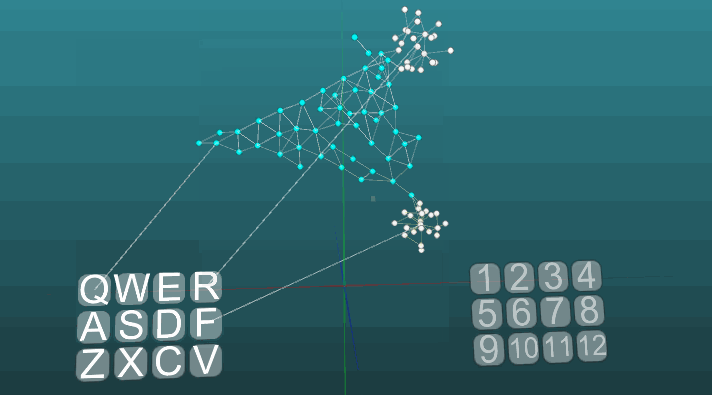至此，我们已经完成了神经系统模型的基础研究。在下一部分中，我们将考虑应用的事物，如何使用所有这些来模拟记忆，情绪和神经元的特化。