如果我们回顾研究从地球到月球的飞行路径的历史，那么您需要追溯到一个半世纪前的1865年，当儒勒·凡尔纳的新小说《从地球到月球以直接方式在97小时20分钟内》出版时。当然，这与描述这种飞行的第一本书相去甚远，但这是作者决定从科学的角度对旅行进行描述的第一本小说。而且，由于第一次不仅仅显示了太空旅行，而且还详细分析了所有细微差别，有时很小，因此，本文的准备水平现在得到了特别的了解。现在他们喜欢批评这部小说的作者所犯的错误。但是，由于工作量如此之大，如果根本没有错误，那将是令人惊讶的！现在，不是他的失误使他更加惊奇，而是他的正确想法。例如，Columbia壳和联盟号航天器上的氧气净化系统的想法非常相似。只有儒勒·凡尔纳（Jules Verne）具有氢氧化钠，现在使用氢氧化锂。
尽管假设不正确，但更对的是他正确的时刻。例如，佩雷尔曼（Perelman）批评他提供了从地球到月球飞行时间的错误数据，甚至以小说的名义进行了记录。数学家通过指定的方法进行了更准确的计算，得到了大约六天的数字，比小说中的数字多了两天。在这种方法的框架内，他的计算确实是正确的。实际上只有四天就可以飞向月球（事实上，许多设备大约是在这个时候到达月球的），但是六天之内已经不可能了，科幻小说家错误地选择了计算方法，但事实证明这个数字是正确的！仍然，例如，在小说《绕月》发行后不久，许多人怀疑仅靠重力的作用，月球近距离飞越的轨迹是否可行。直到二十世纪初，当评估双星系统中的轨道时，才真正显示出存在这种轨道的可能性。以下是20世纪初英国期刊《知识》在《儒勒·凡尔纳的天文学》一文中写道：«, . , . . , . , , . , , , . . . . , . , , , ».换句话说，儒勒·凡尔纳（Jules Verne）当时试图解决的任务不仅位于科学的前沿，还常常提出科学无法回答的问题。但是，一定不要忘记他不是一个人做这一切。在撰写所有书籍时，作者试图寻求任何领域的专家。根据他的日记，从地球到月球飞行的计算是由他的堂兄亨利·加斯（Henri Garce，1815-1871年）进行的，亨利·加斯是拿破仑大学（现为亨利四世）的数学老师。顺便说一句，在这里您可以看到他的法语书籍，该书籍专门研究了Leçonsnouvelles de Cosmographie（1854年）的宇宙学。而且他的计算非常准确。例如，在这里，根据书中的数据，我计算了Columbiada机组人员的确切开始日期。
亨利·加斯（Henri Garcet，1815–1871年），但是，如果儒勒·凡尔纳（Jules Verne）没有将它们放在“绕月”一书的开头，而是在与Columbiada炮弹的船员交谈时使用它们，我们可能不会知道他的计算。他们写道，1869年11月7日的《辩论》报纸的读者看到如此复杂的数学计算真是感到惊讶-这本小说的出版始于这家报纸。这是通过米歇尔·阿丹（Michel Ardan）和巴比肯（Barbicane）的嘴形容飞行的数学模型的方式：“巴比肯，你知道吗，我整夜都在想什么？”
-那呢？主席问。
— . , , , . : , , , .
— , — , — , , , , , .
— , , — .- - ?
— .
— ?
…
“是的，亲爱的朋友。”考虑到问题的所有已知条件：
从地球中心到月球中心的距离，地球半径，地球质量，月球质量，我可以准确确定我们的弹丸的初始速度，同时使用最简单的公式。
-公式是什么？
-但是你知道。但是，考虑到它们围绕太阳的相对运动，只有我不会越过我们的壳在月球和地球之间描述的曲线。假设两个行星都静止不动。这样就足够了。
-为什么？
-由于这是解决“三体任务”的任务的方法，因此尚未充分开发出解决此类问题的整体方法。不久之后，该公式也被介绍给读者：其中r是地球的半径，是地球中心与月球之间的距离，x是核心与地球的距离，V 0是核心的初始速度。V是x距离处的速度。飞行看起来像这样在这里，我想指出的是，带有指示的初始数据的公式确实是正确的。它确实可以在任何给定时间准确地显示地球和月球对设备的引力作用。从能量守恒定律很容易得出。Verne-Garce公式的推导
mv2 / 2 – γMm/R – γMm/R =const
m M,M – , ,
γ – , R - , R-
. .
mv2 / 2 – γMm/x– γMm/(D-x) =mv02 / 2 – γMm/r – γMm/(d-r)
m,
v2 / 2 –v02 / 2=γM/x+ γM/(D-x)– γM/r – γM/(d-r)
1/2*(v2-v02 )=γM(1/-1/r+M/M*1/(d-x)-M/M*1/(d-r))
1/2*(v2-v02 )=γM/r(r/-1+M/M(r/(d-x)-r/(d-r))
mg=mγM/r2 γM=g*r2
1/2*(v2-v02 )=gr(r/-1+M/M(r/(d-x)-r/(d-r))
那怎么办？问题在于它没有考虑系统的动态性。月亮以大约1 km / s的速度绕地球旋转。这正是这个问题的问题。结果，当尝试按照上述方案飞行时，当该站飞行到地球与月球之间的中性点时，它根本不会被月球场捕获，因为月球场将以每秒一公里的速度从弹丸飞走，并且弹丸将开始坠落到地球上。但是后来有希望的是，仍然会发生由月球捕获装置的情况，并且类似的方案（近似地）可以准确地显示飞行的动态。在儒勒·凡尔纳（Jules Verne）的帮助下，一种类似的计算飞行距离的方法很快变得非常流行。它不仅开始用于艺术书籍中，而且还用于严肃的科学作品中。应该注意的是，那时天文学家只是了解了考虑动力学的重要性。是的，考虑到重力和动力学的微分方程可以很容易地组成。只是也找不到简单的解决方案。实际上，众所周知，三体问题没有通用的解析解，只能通过数字方式解决，这意味着非常大量的常规计算，可能要花费数月甚至数年的时间。在小说出版时，类似的问题在数值上仅被解决了两次。此外，第一次尝试是在1759年小说出版前一百多年。众所周知，埃德蒙·哈雷（Edmund Halley）在编制彗星目录时注意到，在不同时间出现在天空中的几颗彗星具有非常相似的参数。在验证了它们之后，他决定它可能是同一颗彗星。然后，将以他的名字呼唤她。哈雷彗星分别于1531年，1607年和1682年出现在天空中。也就是说，循环周期为75-76年，科学家预测1758年会再次出现。一切都将是美好的，即使不是一个“而是”：在估计的时间，天空中的彗星永远不会露面。然后，法国数学家克莱奥决定尽可能精确地计算其轨迹。其中包括考虑到由于木星和土星的吸引力而对其轨迹产生的扰动。尽管他并非独自完成这项工作，但这项工作非常累人且漫长：他得到了天文学家J. Lalande和数学家Lepot夫人的协助。事实证明，与先前估计的彗星自转周期相差618天，它将在1759年4月13日到达其近日点。一个月可能出现错误。评估结果非常准确：这颗彗星于3月12日通过了近日点。这既是数学家的胜利，也是牛顿定律的很好的证明。关于这一计算，拉兰德后来写道：我们从早上到晚上计算了六个月，有时甚至没有从食物里抬起头来，其结果是我一生中的大部分时间都感到不适。勒波特夫人的帮助是这样的，没有她，我们将永远不敢承担这项艰巨的工作，其中包括计算150年来天球每度的彗星与木星和土星两个行星的距离。“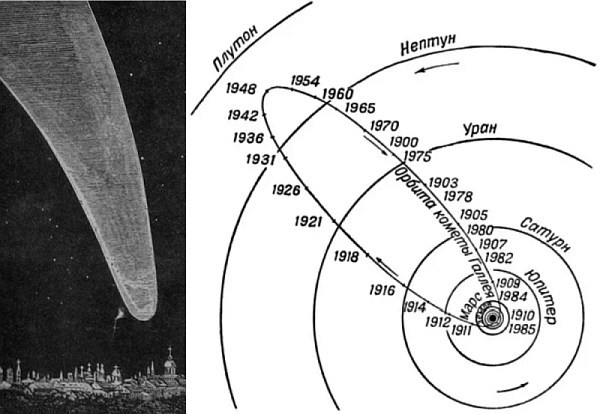
您可以看到哈雷彗星相对于轨道的轨迹行星数在1829年第二次使用类似的方法，再次计算了哈雷彗星的轨迹。估算给出了彗星1835年11月15日返回太阳的日期。彗星于11月16日返回，仅晚了一天。结果，类似的数值方法证明了其准确性。但是从上面的故事中，您可以清楚地看到需要完成多少繁琐的工作。由三名数学家进行的六个月的工作仅计算了一条具有众所周知的初始参数的轨迹！但是，要计算从地球到月球的飞行轨迹，有必要使用不同的初始参数来评估数十个（如果不是数百个）轨迹。否则，就不可能获得确切的速度，发射日期，轨迹特征，可能的误差，月球附近月球站的飞行参数等信息。这可能要花费数年的时间。也就是说，该解决方案被认为是非常困难的。特别是对于没有太多实际意义的任务。同时，当时也有信心可以找到三体问题的解析解。在第一近似中，至少允许评估飞行参数。Jules Verne提出的方法似乎可以回答这个问题。毕竟，在数学上，在最初的假设框架内，他是无可挑剔的。是的，他没有考虑动力学，但随后许多人期望这个假设是正常的，并且从地球到月球的弹丸的真实轨迹看起来像这样。根据《宇宙飞船》一书计算。 （小说家幻想中的行星际通信）“ 1928年，数学之美，再加上小说的盛行，开了一个残酷的玩笑：使用这种方法，几乎所有太空探索的先驱者- 戈达德，斯特恩费尔德，奥伯特，马克斯·瓦尔等都对飞行进行了评估。有时，极少数情况下，他们还估计不是直接飞行，而是根据地球卫星的椭圆形。但是这种方法也有其缺点。例如，由于某种原因，许多人确信到达月球足以使其进入其作用范围。他们说，此外，月亮的吸引力应该做其余的事情。尽管如上所述，但是已经证明了在三体问题中四处飞行的可能性。18 1952 . , , , .
, : , – . , . .
. , - .
.
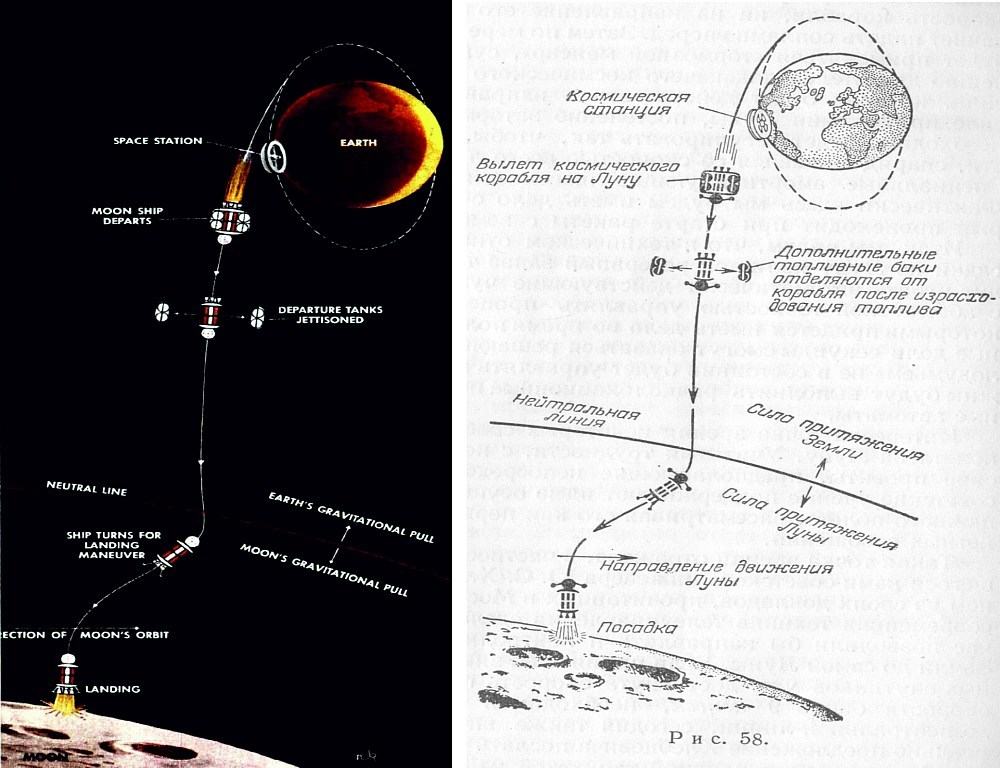
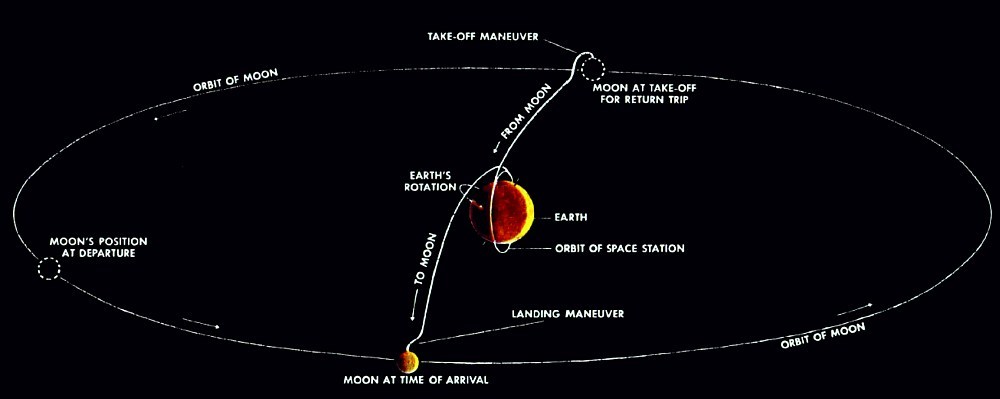