重采样II。声音路径中数字和模拟高阶滤波器操作的比较以及问题的答案
注意-本出版物是本文的 第一部分的澄清，是对本文评论的答复。要了解它的全部含义，如果您尚未熟悉上一 本书，则需要熟悉一下。
在我上一篇文章的众多评论中，有两个非常有特色的问题-一群人，我可以有条件地将其归类为“从业者”，以及一个也许不愿意表达与许多发烧友相似立场的人。对我来说很清楚，并不是每个人都基于信号的频谱分解和谐波的进一步处理理论来理解这些解释。下面，我尝试更清楚地阐明上一篇文章中的某些问题。因此，在猫之下，我们考虑了两个主题：
为什么声音处理路径中的数字滤波器并不总是邪恶的？为什么很难在串行设备中实现高阶模拟滤波器，我将尝试以最容易理解的语言来揭示这两个主题。为什么声音处理路径中的数字滤波器并不总是邪恶的
FreeMind2000的
问题一：? ;)
:
1) -> (16, 44.1 ) -> CD
2) CD -> 16 -> -> (16, 44.1 ) ->
:
2) CD -> 16 -> + ( 16 18, 44.1 44.1*4) -> (18, 44.1*4 ) ->
.. :
1. ( )
2. () CD — - .
?
, , :
1. , , ( ) , ()? , 44.1 — , .
2. ( , :) ? .. , 8 4…
3. ?
20 , 44.1 — ?.. 2 — , , , - ? ;)
是的，奈奎斯特定理是正确的，但是即使可以使用两个频率来恢复周期信号的频率，这一点非常重要，但这并不意味着它可以成功地制作DAC，尤其是在不使用滤波器的情况下！此外，这涉及复杂的信号，该信号是大量谐波的叠加，有时会急剧出现，消失或改变音调。为了找到问题的核心，有必要了解以下内容-在执行了数字化操作之后，我们便不可避免地使信号失真。即使您使用了完美的麦克风，放大器和模数转换器。为了清楚起见，让我们从理论上转到实践上，并以理想DAC发出的信号为背景，描绘原始信号的形状。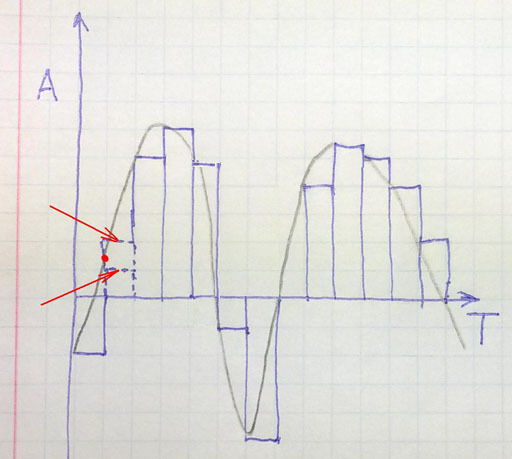
回想一下DAC或用俄语，DAC会定期提取数字化值并将其固定在输出中。结果，我们得到一个阶跃信号。在我们的图中，最小垂直和水平步长等于一个像元。台阶的宽度对应于数字化频率，垂直分辨率由ADC的分辨率确定。在第二位的数字化示例中，可以看到数字化信号的质量如何取决于它。实际值几乎位于两个有效整数值的中间，可以将其分配给ADC样本。它选择了底部，我们犯了一个很大的错误。我希望每个人都理解为什么即使在理想的ADC中，低阶也不能被认为是重要的。
让我们来看看是什么使我们的SONY微电路成为现实。她将采样频率提高了4倍。不仅如此，由于将信号容量从16位增加到18位，她还垂直增加了分辨率。此外，使用该滤波器，可以近似信号并插入三个中间点，其安装精度在水平和垂直方向上都比转换前高4倍。这些点的整齐排列是过滤器。他的阶数越高，产生的近似值越好。但是，执行完这些操作后，我们仍然具有图中未显示的阶梯结构-取而代之的是，我在前三个示例中描绘了粗体点。平滑这些步骤的最简单的二阶或三阶低频滤波器已经进入了业务领域。结果如下所示：
在这里，铅笔曲线是原始信号。红色曲线是16位DAC输出处的信号。曲线的绿色部分是在重新采样操作以及随后应用最简单的滤波器之后得到的结果。我希望FreeMind2000及其支持者同意，“来自DAC输出的纯净无失真的阶跃声音”看起来不像原始的，而是失真的数字失真吗？我注意到，左侧的第一次振荡在44/7 = 6 kHz的某个区域内具有主谐波，而当以44 kHz的频率数字化时，其外观会非常失真。您能想象频率为17 kHz的信号看起来像原始信号吗？在此必须注意，如果需要，数字滤波器可能不会触摸从16位DAC接收到的参考点-只能在它们之间放置辅助参考点，从而根据需要平滑曲线。由于多种原因，不能使用高阶模拟滤波器而不是数字来完成此操作。顺便说一下，现在是时候继续讨论问题了，而不是由安东·索尔（AntonSor）发表并得到德纳斯（Dernuss）热烈支持的声明为什么很难在串行设备中实现高阶模拟滤波器
AntonSor的
评论文本：为了切断超出音频范围（20 kHz）边界的所有信号，并在44 kHz时获得40 dB的衰减，并且具有均匀的相位响应，需要7阶滤波器（偶数是Butterworth滤波器），这是三个运算放大器每个通道10个5％的电阻和电容。是的，笨重，但并非不可能。两个TL074型四路运算放大器。在业余接收机中，存在更多的直接转换（在移相器中）。
为了不参与所有假期的教育计划，我只提到了不能在包括TI TL074的通用运算放大器上构建高质量的高质量滤波器。非常重要的是，高阶模拟低通滤波器会产生严重的相位失真，尤其是在截止频率范围内。为了通过一系列长公式向我们尊敬的同志证明这个众所周知的事实，我也不会，只是给出我上一篇文章的图片，该图片显示了如何用波形处理硬相位失真。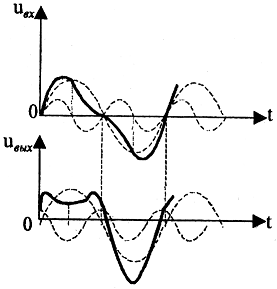
最后，应工人的要求我将详细说明为什么在没有精确选择零件名义值的情况下，高阶滤波器将无法产生漂亮的理想计算特性的原因，如对数坐标中信号衰减对Butterfort滤波器阶次的频率归一化依赖性。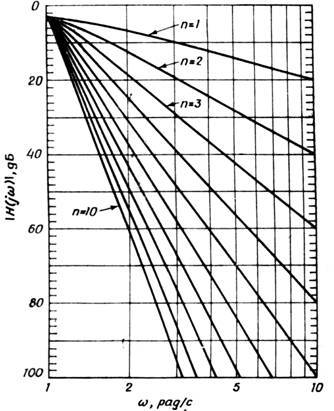
为了构建一个在此参数上接近数字参数的滤波器，如前一篇文章所述，需要八到第十阶。理想低通滤波器和Butterfort滤波器的不同阶次的传递函数如下所示。
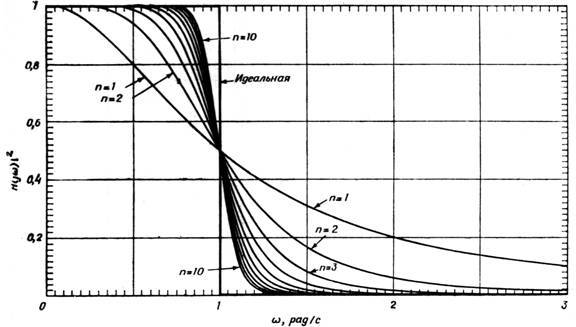通常如何构建此类过滤器？非常简单-例如，根据以下方案构建一个二阶低通滤波器...
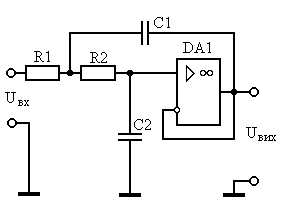很好，让我们看一下一个图表，该图表显示了二阶Butterworth滤波器的参数如何变化；请注意，线性比例是根据反馈电路中组件标称值的分布水平绘制的。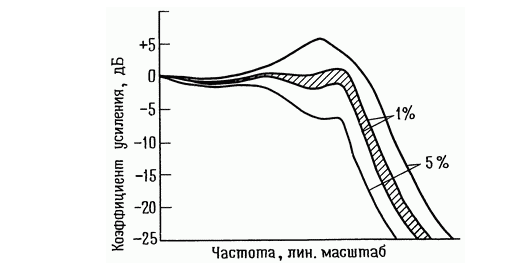
现在想象一下由于组件的扩展，具有不同截止频率的几个此类链路的传输特性的叠加。
很容易猜测，我们将不会获得根据阶数增加滤波器陡度的效果。另外，我们会在特性上产生过多的驼峰，从而引起互调失真。实际上，情况甚至更糟，因为扩展不仅影响截止频率，还影响每个链路的其他参数。由癌症，天鹅和梭子鱼产生的最终滤波声音可能适合再生接收器输出端扬声器的质量，但是尝试在高质量DAC中使用它不会在潜在购买者中引起任何不健康的笑声。而不是后记
我发布了来自zerg59用户的两张图片，而不是一个后记，该用户不太懒惰地模拟Labview中的音频路径带有信号发生器，ADC，DAC和重采样器
DAC输出处的信号的频率为采样频率的0.45。那么看到“零拍”
经过重采样和数字滤波器相同的信号是十阶PS 我忍不住用一个漂亮的评论的标题画面片段上的用户的第一部分电冰箱 Source: https://habr.com/ru/post/zh-CN400527/
All Articles