引言
出现了许多有关量子纠缠的流行文章。 量子纠缠的实验非常壮观,但是没有获奖。 为什么对于外行人来说如此有趣的实验对科学家来说并不有趣? 热门文章谈论成对纠缠粒子的惊人特性-暴露于一个粒子会导致第二个粒子的状态发生瞬时变化。 术语“量子隐形传态”背后隐藏着什么,他们已经开始说这是超光速发生的。 让我们从普通量子力学的角度来看所有这些。
来自量子力学的东西
根据经典的Landau和Lifshitz教科书,量子粒子可以处于两种状态:纯态和混合态。 如果一个粒子不与其他量子粒子相互作用,则用仅取决于其坐标或动量的波动函数来描述它-这种状态称为纯态。 在这种情况下,波动函数服从薛定ding方程。 另一个选择是可能的-粒子与其他量子粒子相互作用。 在这种情况下,波动函数已经指代相互作用粒子的整个系统,并且取决于它们的所有动态变量。 如果我们只对一个粒子感兴趣,那么可以用矩阵或密度算子来描述其状态,如Landau在90年前所展示的。 密度矩阵服从类似于Schrödinger方程的方程
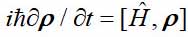
在哪里
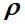
是密度矩阵,
H是哈密顿算子,方括号表示换向器。
兰道把他带了出去。 与给定粒子有关的任何物理量都可以通过密度矩阵表示。 这种情况称为混合。 如果我们有一个相互作用的粒子系统,那么每个粒子都处于混合状态。 如果粒子分散很长的距离,并且相互作用消失了,它们的状态仍将保持混合状态。 如果几个粒子中的每个粒子都处于纯净状态,则该系统的波动函数是每个粒子的波动函数的乘积(如果粒子不同。对于相同的粒子,玻色子或费米子,有必要组成对称或反对称的组合,请参见[1],但是后来,粒子,费米子和玻色子的身份已经是相对论量子论。
一对粒子的纠缠状态是与不同粒子有关的物理量之间具有恒定的相关性的状态。 一个简单且最常见的示例是某个总物理量,例如一对的总自旋或角动量。 一对粒子处于纯状态,但是每个粒子都处于混合状态。 似乎一个粒子状态的变化将立即影响另一粒子的状态。 即使它们分散很远并且不相互作用,这也是流行文章中所表达的。 这种现象已经被称为量子隐形传态,有些文盲的记者甚至声称这种变化是瞬间发生的,也就是说,其传播速度快于光速。
从量子力学的角度考虑这一点:首先,任何仅改变一个粒子的自旋或角动量的动作或测量都立即违反了总特性守恒定律。 相应的操作员无法以全自旋或全角动量上下班。 因此,违反了一对粒子状态的初始纠缠。 第二个粒子的自旋或力矩不再与第一个粒子的自旋或力矩明确关联。 您可以从另一方面考虑此问题。 在粒子之间的相互作用消失之后,每个粒子的密度矩阵的演化由其自己的方程式描述,其中不包括其他粒子的动态变量。 因此,暴露于一个颗粒不会将密度矩阵改变为另一个。
甚至有埃伯哈德定理[2],它声称无法通过测量来检测两个粒子的相互影响。 假设有一个由密度矩阵描述的量子系统。 并让该系统由两个子系统A和B组成。Eberhard定理指出,仅与子系统A相关的可观测量的测量不会影响对仅与子系统B相关的可观测量的测量结果。但是,该定理的证明使用了波动减少假设理论上或实验上尚未证明的功能。 但是所有这些考虑都是在非相对论量子力学的框架内进行的,并且涉及各种不同的粒子。
在一对相同粒子的情况下,这些考虑在相对论中不起作用。 让我再次提醒您,粒子的身份或不可区分性来自相对论量子力学,其中粒子的数量没有保留。 但是,对于慢速粒子,我们可以使用一种较简单的非相对论量子力学设备,只需考虑粒子的不可区分性即可。 然后,相对于粒子的排列,该对的波动函数应该是对称的(对于玻色子)或反对称的(对于费米子)。 相对论理论提出了这样的要求,而与粒子速度无关。 正是这一要求导致了一对相同粒子的长距离相关。 原则上,带有电子的质子也可以处于缠结状态。 但是,如果它们分散几十埃,则与电磁场和其他粒子的相互作用将破坏该状态。 如实验所示,交换相互作用(称为这种现象)在宏观距离上起作用。 一对即使是按米分散的粒子仍然无法区分。 如果要进行测量,则无法确切知道测量值属于哪个粒子。 您正在同时测量一对粒子。 因此,所有壮观的实验都是使用完全相同的粒子-电子和光子进行的。 严格来说,这不是在非相对论量子力学框架中考虑的令人困惑的状态,而是类似的东西。
考虑最简单的情况-一对相同的非相互作用粒子。 如果速度较小,则可以使用非相对论量子力学,并考虑到波函数相对于粒子排列的对称性。 让第一个粒子的波函数
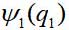
,第二个粒子-
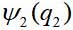
在哪里
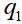
和
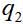
-在最简单的情况下,第一和第二粒子的动态变量-只是坐标。 然后对的波动函数
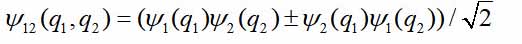
符号+和-指玻色子和费米子。 假设粒子相距很远。 然后

分别位于偏远地区1和2,即在这些地区之外,它们很小。 让我们尝试计算第一个粒子的某个变量的平均值,例如坐标。 为简单起见,我们可以想象波浪函数中仅包含坐标。 事实证明,粒子1的坐标平均值位于区域1和2之间,并且与粒子2的平均值一致。这实际上是自然的-粒子是无法区分的,我们无法知道要测量哪个粒子。 通常,粒子1和2的所有平均值都将相同。 这意味着通过移动粒子1的定位区域(例如,粒子位于晶格缺陷内部,然后移动整个晶体),我们作用在粒子2上,尽管粒子在通常意义上并不相互作用-例如通过电磁场。 这是相对论纠缠的一个简单例子。
由于两个粒子之间的这些相关性,不会发生信息的瞬时传输。 最初建立了相对论量子理论的设备,以使光锥相对两侧的时空事件不会相互影响。 简而言之,没有信号,没有影响或干扰会比光传播得更快。 这两个粒子实际上都是一个电场的状态,例如电子-正电子。 通过在某一点(在粒子1上)作用于电场,我们产生了像水波一样传播的干扰。 在非相对论的量子力学中,光速被认为是无限大的,这造成了瞬时变化的幻觉。
由于关于粒子的经典观念,相距很远的粒子保持成对耦合的情况似乎是自相矛盾的。 我们必须记住,实际上不是粒子,而是场。 我们表示为粒子的只是这些场的状态。 粒子的经典概念完全不适用于微观世界。 立即出现有关基本粒子的大小,形状,材料和结构的问题。 实际上,一个经典粒子就出现了与经典思维矛盾的情况。 例如,在Stern-Gerlach实验中,氢原子飞过垂直于速度的不均匀磁场。 由于核磁子的较小性,可以忽略原子核的自旋;让电子的自旋最初沿速度定向。
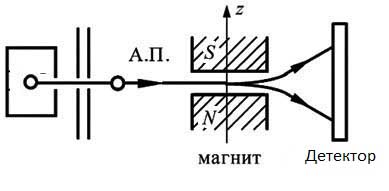
原子波函数的演化很容易计算。 初始的局部波包被分成两个相同的波包,与原始方向成角度对称地飞行。 就是说,一个原子,一个重粒子,通常被认为是具有经典轨迹的经典粒子,分裂成两个波包,可以散射到完全宏观的距离。 同时,我注意到-从计算得出,即使是理想的Stern-Gerlach实验也无法测量粒子自旋。
如果检测器例如化学键合了氢原子,则“两半”(两个散射波包)将组装成一个。 涂抹颗粒的这种定位如何发生是我不理解的另外存在的理论。 有兴趣的人可以找到有关该主题的大量文献。
结论
提出了一个问题-大量实验证明大距离粒子之间的相关性有什么意义? 除了确认量子力学,这是普通物理学家长期以来一直没有怀疑的,这是一次引人注目的演示,给分配科学经费的公众和业余官员印象深刻(例如,Gazprombank赞助了量子通信线路的开发)。 对于物理学而言,这些昂贵的演示虽然可以促进实验技术的发展,但却没有提供任何帮助。
文学作品1. Landau,L. D.,Lifshits,E.M.量子力学(非相对论)。 -第三版,修订和补充。 -M .:娜卡(Nauka),1974年-752页。 -(“理论物理学”,第三卷)。
2. Eberhard,PH,“贝尔定理和非局部性的不同概念”,Nuovo Cimento 46B,392-419(1978)