Geekly articles weekly

汽轮机的线性化流量特性。 第2部分。MATLAB中PT-80涡轮的构造示例

第一部分前言


对蒸汽轮机建模是我们国家数百人的日常工作。 习惯上讲费用特征代替单词模型 。 汽轮机的消耗特性被用于解决诸如计算火力发电厂产生的电力和热的当量燃料的比消耗的问题。 热电联产的优化； 规划和维护火力发电厂模式。


我开发了一种新的蒸汽轮机流量特性- 蒸汽轮机的线性流量特性。 所开发的流动特性在解决这些问题方面既方便又有效。 但是，目前仅在两篇科学论文中对此进行了描述：


  1. 在俄罗斯电力和容量批发市场下优化火力发电厂的运行 ;
  2. 确定联合发电方式下供热能源的火力发电厂当量燃料比消耗的计算方法 。

现在，在我的博客中，我想：




1.源数据


构造线性化流动特性的初始数据可以是


  1. 在蒸汽轮机运行期间测得的实际功率值Q 0 ，N，Q p ，Q t
  2. 规范和技术文件中的总诺模图q t总。

当然，实际的瞬时值Q 0 ，N，Q p ，Q t是理想的源数据。 收集此类数据非常耗时。

如果无法使用Q 0 ，N，Q p ，Q t的实际值， 则可以处理列线图q t gross。 它们又是根据测量获得的。 阅读有关VM Gornstein中的涡轮机测试的更多信息 优化能源系统模式的其他方法 。


2.构造线性化流动特性的算法


构造算法包括三个步骤。


  1. 将列线图或测量结果转换为表格视图。
  2. 汽轮机流动特性的线性化。
  3. 确定汽轮机控制范围的边界。

使用列线图q t gross时，第一步很快速。 这项工作称为数字化 。 对于当前示例，数字化9列线图花费了我大约40分钟的时间。


第二步和第三步需要使用数学软件包。 我爱和使用MATLAB多年。 我以构造线性化流动特性为例。 可以从链接下载示例，运行并独立找出构造线性化流量特性的方法。


该涡轮机的流量特性是根据以下模式参数的固定值构建的：


  • 单阶段操作
  • 中压蒸汽压力= 13 kgf / cm2，
  • 低压蒸汽压力= 1 kgf / cm2。


Chuchueva-PT-80-linear-characteristic-curve.rar存档的内容 。


1） 发电总单位消耗量qt的正线图 （带标记的红点数字化-转移到表格中）：


  • PT80_qt_Qm_eq_0_digit.png，
  • PT80_qt_Qm_eq_100_digit.png，
  • PT80_qt_Qm_eq_120_digit.png，
  • PT80_qt_Qm_eq_140_digit.png，
  • PT80_qt_Qm_eq_150_digit.png，
  • PT80_qt_Qm_eq_20_digit.png，
  • PT80_qt_Qm_eq_40_digit.png，
  • PT80_qt_Qm_eq_60_digit.png，
  • PT80_qt_Qm_eq_80_digit.png。

2） 数字化的结果 （每个csv文件对应一个png文件）：


  • PT-80_Qm_eq_0.csv，
  • PT-80_Qm_eq_100.csv，
  • PT-80_Qm_eq_120.csv，
  • PT-80_Qm_eq_140.csv，
  • PT-80_Qm_eq_150.csv，
  • PT-80_Qm_eq_20.csv，
  • PT-80_Qm_eq_40.csv，
  • PT-80_Qm_eq_60.csv，
  • PT-80_Qm_eq_80.csv。

3）具有计算和图形化功能的MATLAB脚本 ：


  • PT_80_linear_characteristic_curve.m

4） 将列线图数字化的结果和以表格形式构造线性化流量特性的结果 ：


  • PT_80_linear_characteristic_curve.xlsx。

步骤1.将列线图或测量结果转换为表格视图


1.源数据处理


本例的初始数据是列线图q t总。


要数字化许多列线图，您需要一个特殊的工具。 我已经多次将Web应用程序用于这些目的。 该应用程序简单，方便，但是没有足够的灵活性来自动化该过程。 部分工作必须手动完成。


在此步骤中， 重要的是数字化定义了汽轮机调节范围边界的列线图的极限点 。


工作是使用该应用程序在每个png文件中标记放电特性的点，下载生成的csv并将所有数据收集在一张表中。 数字化的结果可以在文件PT-80-linear-characteristic-curve.xlsx，工作表“ PT-80”，表“输入数据”中找到。


2.将计量单位转化为动力单位


接下来，在工作表“ PT-80”上，我们根据公式计算Q 0的值

$$显示$$ \开始{equation} Q_0 = \ frac {q_T \ cdot N} {1000} + Q_P + Q_T \ qquad（1）\ end {equation} $$显示$$


然后将所有初始值都带到MW。 使用MS Excel进行计算。


结果表“输入数据（单位功率）”是算法第一步的结果。


步骤2.汽轮机流量特性的线性化


1.测试MATLAB


在这一步，您需要安装并打开不低于7.3的MATLAB版本（这是旧版本，当前为8.0）。 在MATLAB中，打开文件PT_80_linear_characteristic_curve.m，运行该文件并确保其正常运行。 一切正常，如果在命令行上运行脚本的结果显示以下消息：


    PT_80_linear_characteristic_curve.xlsx  1  : a(N) = 2.317, a(Q) = 0.621, a(Q) = 0.255, a0 = 33.874   = 0.006, (0.57%)      = 37

如果有任何错误，请自己弄清楚如何解决。


2.计算


所有计算都在文件PT_80_linear_characteristic_curve.m中实现。 让我们分部分考虑它。


1）我们指出源文件的名称，工作表，包含上一步中获得的“源数据（容量单位）”表的单元格范围。


 XLSFileName = 'PT_80_linear_characteristic_curve.xlsx'; XLSSheetName = 'PT-80'; XLSRange = 'F3:I334';

2）我们在MATLAB中读取源数据。


 sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange); N = sourceData(:,1); Qm = sourceData(:,2); Ql = sourceData(:,3); Q0 = sourceData(:,4); fprintf('    %s  %1.0f \n', XLSFileName, toc);

我们使用变量Qm表示蒸汽的平均流量Q p ， 中间的指数m为平均值。 类似地，我们将变量Ql用于低压蒸汽流量Q n ，从低开始的指数l低。


3）定义系数αi 。


回顾流动特性的通用公式

$$显示$$ \开始{equation} Q_0 = f（N，Q_，Q_）\ qquad（2）\ end {equation} $$ display $$



并指定独立变量（x_digit）和因变量（y_digit）。


 x_digit = [N Qm Ql ones(size(N,1),1)]; %  N,   Q,   Q,   y_digit = Q0; %    Q0

如果您不了解x_digit矩阵为何只有一个向量（最后一列），请阅读线性回归资料。 关于回归分析的主题，我推荐Draper N.，Smith H. 应用回归分析这本书。 纽约：威利，印刷中，1981年。693页。 （俄语）。


汽轮机线性化流动特性方程


$$显示$$ \开始{等式} Q_0 = \ alpha_N \ cdot N + \alpha_\ cdotQ_+ \alpha_\ cdotQ_+ \ alpha_0 \ qquad（3）\结束{等式} $$显示$$



是多元线性回归模型。 系数αi将使用“文明的最大利益” （最小二乘法）确定。 另外，我注意到最小二乘法是高斯在1795年开发的。


在MATLAB中，这是一行完成的。


 A = regress(y_digit, x_digit); fprintf(': a(N) = %4.3f, a(Q) = %4.3f, a(Q) = %4.3f, a0 = %4.3f\n',... A);

变量A包含所需的系数（请参见MATLAB命令行上的消息）。


因此，获得的PT-80蒸汽轮机的线性化流动特性具有以下形式


$$显示$$ \开始{equation} Q_0 = 2.317 \ cdot N + 0.621 \ cdotQ_+ 0.255 \ cdotQ_+ 33.874 \ qquad（4）\ end {equation} $$显示$$


4）我们估计获得的流量特性的线性化误差。


 y_model = x_digit * A; err = abs(y_model - y_digit) ./ y_digit; fprintf('  = %1.3f, (%4.2f%%)\n\n', mean(err), mean(err)*100);

线性化误差为0.57％ （请参见MATLAB命令行上的消息）。


为了评估使用蒸汽轮机的线性化流量特性的便利性，我们解决了在已知负载值N，Q p和Q t下计算高压蒸汽流量Q 0的问题。


令N = 82.3 MW，Q p = 55.5 MW，Q t = 62.4 MW，则


$$显示$$ \开始{等式} Q_0 = 2.317 \ cdot 82.3 + 0.621 \ cdot 55.5 + 0.255 \ cdot 62.4 + 33.874 = 274.9 \ qquad（5）\结束{等式} $$显示$$


让我提醒您，平均计算误差为0.57％。


让我们回到这个问题，为什么汽轮机的线性化流动特性从根本上比发电量的单位消耗量q t的总图更方便？ 要了解实践中的根本差异，请解决两个问题。


  1. 使用列线图和您的眼睛以指定的精度计算Q 0 。
  2. 使用列线图自动计算Q 0的过程。

显然，在第一个任务中，用肉眼确定q个总值充满了总误差。


第二项任务很繁琐。 由于q q值基本上是非线性的 ，因此对于这种自动化，数字化点的数量比当前示例大10倍。 仅数字化是不够的，还必须实现用于对非线性总值进行插值 （在点之间找到值）的算法。


步骤3.确定汽轮机调节范围的边界


1.计算


为了计算调整范围，我们将使用另一种“文明的善” -凸包法，凸包。


在MATLAB中，此操作如下进行。


 indexCH = convhull(N, Qm, Ql, 'simplify', true); index = unique(indexCH); regRange = [N(index) Qm(index) Ql(index)]; regRangeQ0 = [regRange ones(size(regRange,1),1)] * A; fprintf('     = %d\n\n', size(index,1));

convhull（）方法确定由变量N，Qm，Ql的值给出的调整范围的边界点 。 变量indexCH包含使用Delaunay三角剖分构造的三角形的顶点。 regRange变量包含调整范围的边界点； variable regRangeQ0-控制范围边界点的高压蒸汽流量。


计算结果可以在文件PT_80_linear_characteristic_curve.xlsx中的表格“ PT-80结果”中的表“调整范围边界”中找到。


建立了线性化的流量特性。 它是公式（4）和37个点，这些点定义了相应表中调整范围的边界（外壳）。


2.验证


在使计算过程自动化时，Q 0必须检查具有N，Q p和Q t值的某个点是否在调整范围内还是在调整范围之外（该模式在技术上不可行）。 在MATLAB中，可以按照以下步骤进行操作。


我们设置要检查的N，Q p ，Q t的值。


 n = 75; qm = 120; ql = 50;

我们检查。


 in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2)); in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3)); in = in1 && in2; if in fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f     \n', n, qm, ql); else fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f      ( )\n', n, qm, ql); end

验证分两个步骤进行：


  • 变量in1指示N，Q p的值是否已经落入壳在轴N，Q p上的投影中；
  • 类似地，变量in2显示Q p ，Q t的值是否在壳在Q p ，Q t轴上的投影内。

如果两个变量都等于1（true），则所需点在壳体内，这将设置蒸汽轮机的调节范围。


汽轮机获得的线性化流动特性的图示


就说明计算结果而言，我们获得的“文明的最大好处” 。


首先我们要说的是，在其中构造图的空间，即具有x-N，y-Qt，z-Q 0 ，w-Qp轴的空间称为状态空间 （请参见条件下火电厂运行的优化俄罗斯电力和容量批发市场

） 该空间的每个点都定义了蒸汽轮机的某种操作模式。 模式可能是


  • 在技​​术上可行，如果该点位于定义调整范围的外壳内，
  • 如果该点在此外壳之外，则从技术上讲是不可行的。

如果我们讨论蒸汽轮机的冷凝运行模式（Q p = 0，Q t = 0），那么线性化的流动特性就是一条直线段 。 如果我们谈论的是T型涡轮机，则线性化的流动特性是三维状态空间中的平面多边形 ，其轴x-N，y-Q t ，z-Q 0易于观察。 对于PT型涡轮机而言，可视化是最困难的，因为这种涡轮机的线性化流动特性在四维空间中是平坦的多边形 （有关说明和示例，请参阅俄罗斯批发电力市场中的优化火力发电厂的运行， 涡轮流动特性的线性化一节）。


1.汽轮机获得的线性化流动特性的图示


让我们在方案空间中构建“输入数据（功率单位）”表的值。




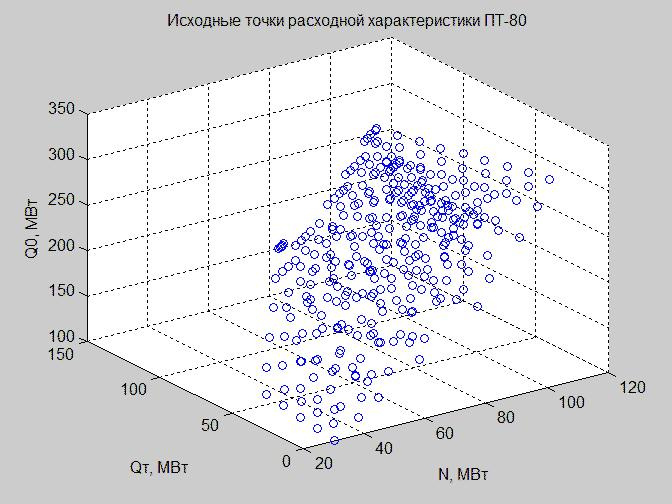
图 3.沿x-N，y-Q t ，z-Q 0轴的状态空间中流动特性的起点


由于我们无法在四维空间中建立依赖关系，因此我们尚未达到如此良好的文明水平，因此我们对Q n的值进行如下操作：排除它们（图3），修正（图4）（请参见在MATLAB中构造图形的代码）。


我们确定Q p = 40 MW的值，并构造起点和线性化的流量特性。




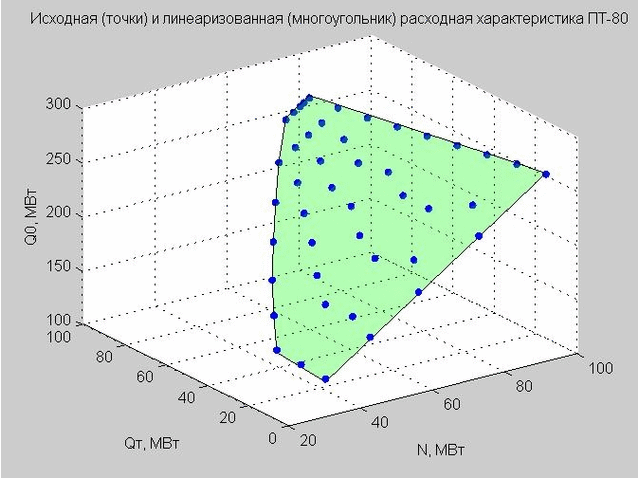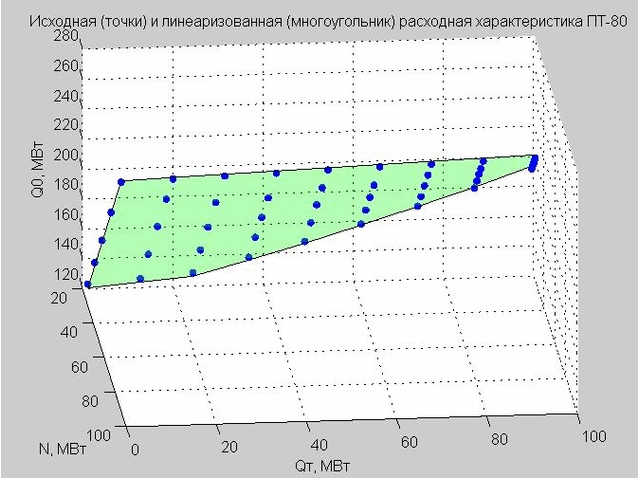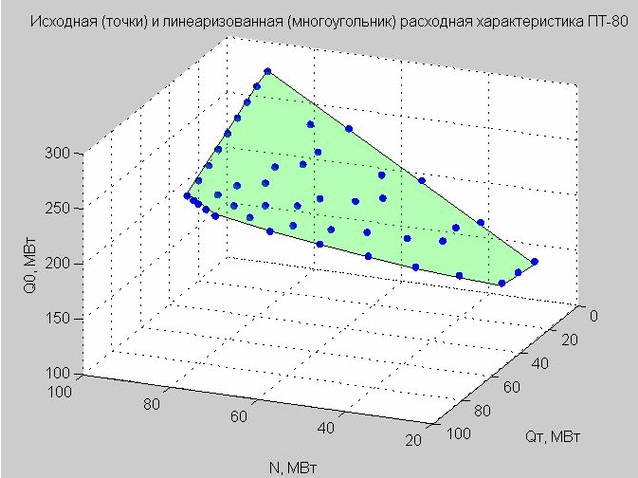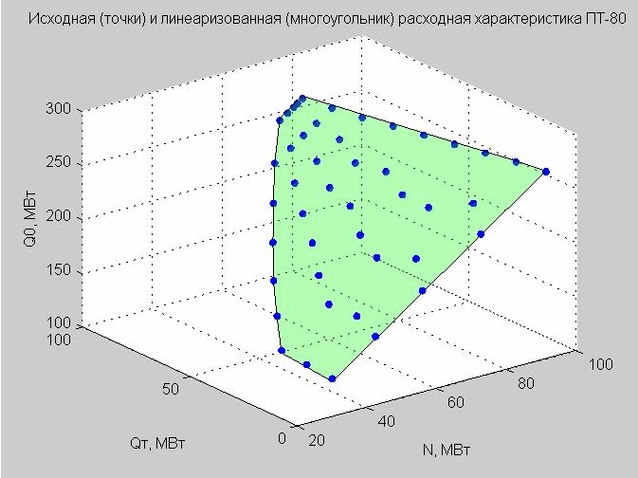
图 4.放电特性的起点（蓝色点），线性放电特性（绿色的平面多边形）


让我们返回获得的线性化流量特性（4）的公式。 如果我们固定Q p = 40 MW MW，则公式将具有以下形式


$$显示$$ \开始{equation} Q_0 = 2.317 \ cdot N + 0.255 \ cdot Q_T + 58.714 \ qquad（6）\ end {equation} $$显示$$


该模型类似于T型涡轮机（在图4中看到），在三维空间中以轴x-N，y-Q t ，z-Q 0定义了平面多边形。


许多年前，当开发了q个总诺模图时，在分析初始数据的阶段就犯了一个基本错误。 他们没有应用最小二乘方法并出于未知原因构造汽轮机的线性化流量特性，而是进行了原始计算：


$$显示$$ \开始{equation} Q_0（N）=Q_= Q_0-Q_-Q_\ qquad（7）\ end {equation} $$显示$$


从高压蒸汽的流量Q 0减去蒸汽的流量Q t ，Q p ，并将产生的差Q 0 （N）= Q e归因于发电。 将获得的值Q 0 （N）= Q e除以N，并转换为kcal / kW·h，同时接收到特定消耗q t gross。 此计算不符合热力学定律。


亲爱的读者，也许您知道未知的原因？ 分享吧！


2.汽轮机调节范围示意图


让我们看一下政权空间中调整范围的外壳。 其构建的起点在图2中给出。 5.这些与我们在图5中看到的相同。 然而，如图3所示，现在排除了参数Q 0 。




图 5.沿x-N，y-Q p ，z-Q t轴的状态空间中流动特性的起点


图中有很多要点。 5是凸的。 使用凸面（）函数，我们定义了定义此集合外壳的点。


Delaunay三角剖分 （一组连接的三角形）使我们能够构建调整范围的外壳。 三角形的顶点是所考虑的PT-80汽轮机调节范围的边界值。




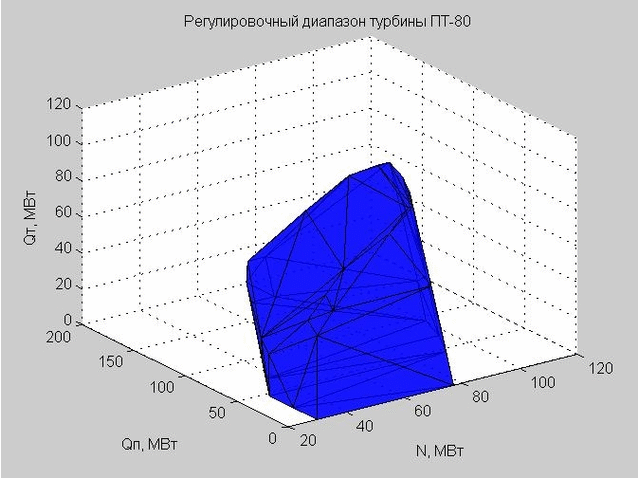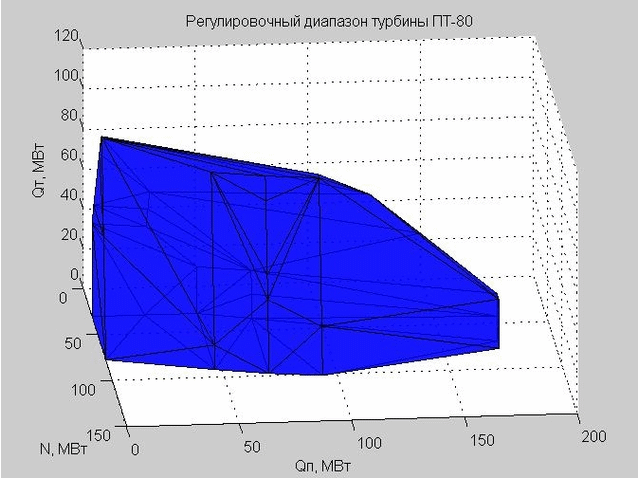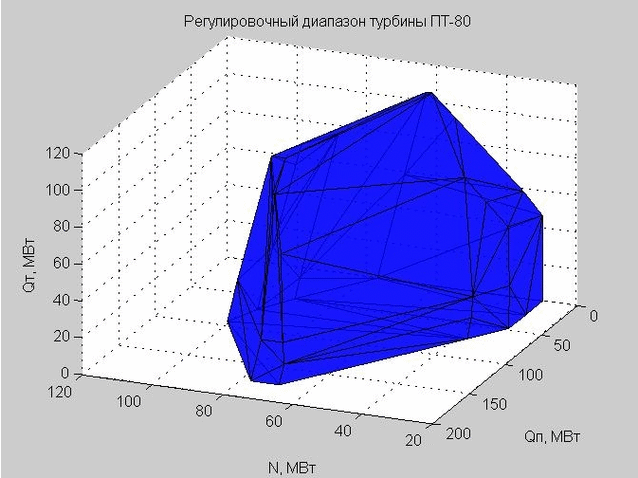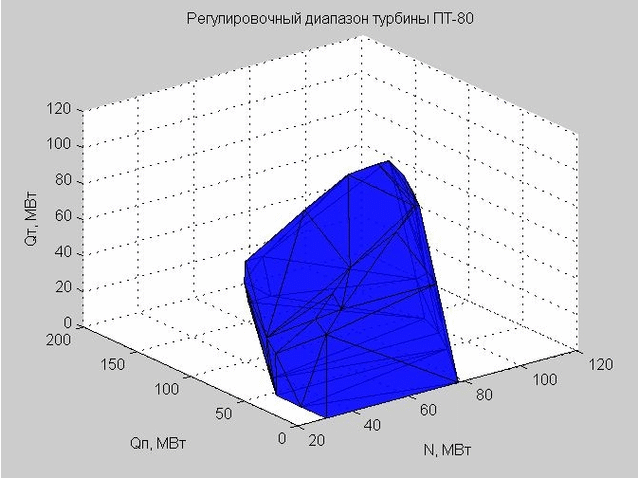
图 6.调整范围的外壳，由许多三角形表示


当我们检查某个点以使其进入调整范围之内时，我们检查了该点是在所得壳的内部还是外部。


上面介绍的所有图形都是使用MATLAB工具构建的（请参见PT_80_linear_characteristic_curve.m）。


与使用线性化流动特性分析汽轮机运行有关的有前途的任务


如果您正在攻读文凭或学位论文，我可以为您提供多项任务，您可以轻松地向全世界证明这些任务的科学新颖性。 另外，您将做一个出色而有用的工作。


任务1


说明当低压蒸气压Q t变化时，平面多边形如何变化。


任务2


显示冷凝器中压力变化时平面多边形如何变化。


任务3


检查线性化流量特性的系数是否可以表示为状态的其他参数的函数，即：


$$显示$$ \开始{equation} \ alpha_N = f（p_ {0}，...）; \\ \ alpha_P = f（p_ {P}，...）; \\ \ alpha_T = f（p_ {T}，...）; \\ \ alpha_0 = f（p_ {2}，...）。 \ end {equation} $$显示$$



这里p 0-高压蒸汽压力，p p-中压蒸汽压力，p t-低压蒸汽压力，p 2-冷凝器中的排气蒸汽压力，所有单位均为kgf / cm2。


证明结果合理。


参考文献


Chuchueva I.A.，Inkina N.E. 俄罗斯电力和容量批发市场条件下的热电联产优化//科学和教育：MSTU科学版。 N.E. 鲍曼 2015年。第8号。S。195-238。



Chuchueva I.A. 确定联合发电模式下火电厂提供的电能和热能的当量比燃料消耗的计算方法//科学和教育：MSTU的科学出版物。 N.E. 鲍曼 2016.第2号，第135-165页。



汽轮机的线性化流量特性。


Source: https://habr.com/ru/post/zh-CN404049/

More articles:


All Articles