质量，能量，动量和守恒定律

世界上许多晦涩的属性与质量和能量（以及动量）的性质有关。 我们都听过这些话，而且我们许多人对其含义含糊不清。 当然，英语和其他语言中“质量”和“能量”一词的含义很多。 不幸的是，它们都不符合物理学家的想法。 尝试撇开单词的这些含义并使用确切的物理概念-否则您将完全困惑。

应当指出，一个人不应该回想起另一种流行的对，即“物质和能量”，用短语“质量和能量”。 许多人提到最后一个短语，就好像物质和能量是同一枚硬币的两个方面一样。 但是事实并非如此。 物质和能量分为不同的类别，例如苹果和猩猩。 物质，无论如何定义，都是宇宙中存在的一类物体，质量和能量不是物体，而是这些物体所具有的特性。 质量和能量相互交织在一起，应作一般性解释。

要了解质量和能量，您需要增加它们的动力，并讨论这些量的差异和关系。

能量

“能源”一词有许多含义。 当我们生病时，我们说我们没有能量，指的是力量和动力。 当我们说某人充满活力时，我们指的是他的活跃。 我们抱怨能源价格上涨，指的是燃料。 我们说的是精神能量，这是无法衡量的，但很重要，也许是某种形式的魅力。 所有这些概念都相互重叠，因此我们选择一个词来形容它们。 但是在物理学中，能量是完全不同的东西。 从物理学的角度来看，这些定义之一将被错误地与物理混淆。 在物理学中，一个人必须遵守一个物理术语，以免得到错误的答案并且不会完全困惑。

不幸的是，物理学中的“能量”概念很难用字典来形容-用一个简短的有意义的短语。 但是不要认为不好-整体来说，这是自然语言的不完美之处，而不是物理学中的能量概念含糊不清。 在任何给定的物理系统中，无论是实验测量还是计算（如果有描述系统的方程式），都完全清楚其能量是多少。

能量难以描述的原因之一是它可以采用多种形式，但并非所有形式都易于理解。 这是三个常见的品种：

1.能量可以包含在物体的质量中。 在这里，我将此选项称为“质量能”（由于众所周知的方程E = mc ^2，该能量绑定到质量。它也称为“静止能量”，因为这是静止的物体（即不运动）的能量）。

2.其次，能量与物体的运动有关。 在这里，我称其为“运动能”，其技术术语为动能。 从直观上讲，此选项易于掌握，因为快速移动的对象比慢速移动的对象具有更多的能量。 另外，与以相同速度运动的轻物体相比，重物体具有更多的运动能量。

3.能量可以存储在对象之间的关系中（通常称为“势能”）。 它被储存在一个伸展的弹簧中，在大坝后面的水中，在地球和太阳的引力相互作用中，在分子中原子的相互作用中。 有很多存储能量的方法。 听起来含糊不清，但应归咎于语言。 在任何一种情况下，都有精确的公式来描述系统中存储的能量以及定义明确的测量方法。

第三种能量与我称之为交互作用的能量有关，这是最混乱的概念。 与质量的能量和运动的能量始终大于或等于零不同，交互作用的能量可以为正和负。 到目前为止，我将离开这个主题，但是我们将回到它。

能量是对物理学非常重要的特殊数量。 这种重要性的原因是它是“保留的”。 这是什么意思？

如果您从一个对象或一组对象开始观察-我们将它们称为“对象系统”-在初始时刻具有一定量的能量（不要忘记计算所有能量-质量，运动，所有类型的存储能量等），然后系统的各个部分将仅彼此相互作用，而没有其他相互作用，那么在观察结束时，这些物体所拥有的总能量将与开始时相同。 系统的总能量得以保存-其总量不变。 它可以改变形状，但是如果您跟踪所有品种，那么最后它会和开始时一样多。

即使某些对象消失并让位于其他对象，例如，如果系统中的一个粒子衰减为两个其他粒子并入系统 ，该规则也会起作用。

为什么要节能？ 由于数学原理，自然定律不会随着时间变化而改变，这与守恒量的存在相关，我们定义为“能量”。

我们将此原理最著名，最笼统的定义归功于爱因斯坦的当代人，上个世纪最伟大的数学物理学家之一艾美·诺瑟 （ Emmy Noether） 。 物理和数学社区的一些成员对她深表敬意 ，但是当时在她的家乡德国，她遭受了基于性别和国籍的歧视（他们阻止了为她分配哥廷根教授头衔的企图，从那以后她不得不逃离纳粹上台）。 移民到美国后，在布林·马学院（ Brin-Mar College）任教仅两年（目前仅接受女性培训），之后她死于癌症。

著名的Noether定理 （实际上是两个密切相关的定理）告诉我们，如果自然定律存在对称性-在我们的情况下，这意味着自然定律在任何时刻都是相同的-那么这将保留一定的量-在我们的情况下，能量。

而且，该定理准确地告诉我们幅度是多少-给定对象系统要添加以获取总能量的能量的不同形式是什么？ 这就是为什么物理学家总是确切地知道什么是能量，以及为什么使用方程式获得比用词来定义更容易的原因。

冲动

动量的情况与能量的情况大致相同。 自然法则到处都是一样的。 粗略地说，无论是在建筑物的北部还是在深井中，无论是在这里的北部还是南部，西部还是东部，这些实验都能给出相同的答案。 在空间中选择任何方向。 然后，根据Noether，沿该方向的动量得以保留。 由于空间存在三个维度，因此可以在三个不同的独立方向上移动，并且存在三个独立的守恒定律。 您可以选择三个方向，只要它们不同即可。 例如，您可以选择南北，西向和上下方向的脉冲作为三个守恒定律。 或者，您可以选择其他三个选项-往返于太阳的方向，沿地球轨道的两个方向以及相对于太阳系平面的上下方向。 您的选择无关紧要，因为动量是沿任何方向存储的。

脉冲的最简单形式是由于对象的简单移动而引起的，这可以直观地想象：如果对象沿某个方向移动，则它在该方向上具有脉冲，并且移动得越快，该脉冲就越大。 如果以相同的速度移动，较重的物体将比轻的物体具有更大的动量。

这种守恒的有趣结果之一：如果您有一个静止的对象系统（即，如果对组成对象的所有运动进行平均，则该系统作为一个整体都不会移动），那么它将保持静止，除非对其进行任何外部移动影响。 原因是在固定系统中，总动量为零，并且由于动量得以维持，因此除非有系统外部的干预，否则动量将永远保持零。

质量及其与能量和动量的关系

现在让我们转向大众

不幸的是，与质量有关的混乱很多-爱因斯坦有关相对论的著作发表一段时间以来，有两个质量概念。 而且只有其中之一（爱因斯坦本人停下来的那个，有时被称为“不变质量”或“静止质量”，以区别于已经成为古老的术语“相对论质量”），仍然在粒子物理学中使用。 在另一篇文章中，我将对此进行详细说明。


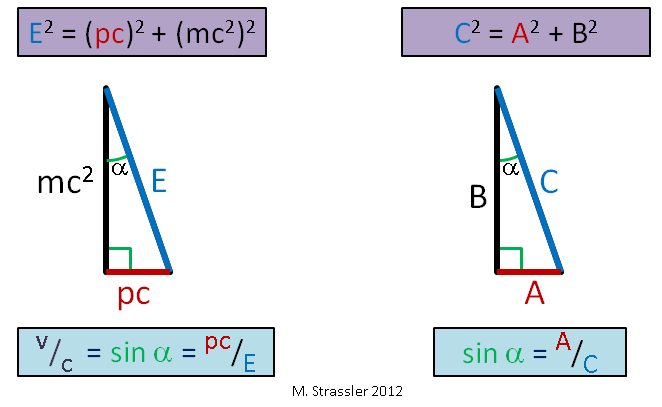图 1个

我在文章中使用的质量m表示直接束缚能量和动量的质量。 对于在不受外力影响的情况下运动的物体（与其他物体没有显着相互作用），爱因斯坦建议（并且已通过实验确认）其能量E，动量p和质量m满足简单的勾股定律：

$$

$$E ^ 2 =（p c）^ 2 +（mc ^ 2）^ 2 \ qquad（等式1）$$

还记得旧毕达哥拉斯（Pythagoras），他声称对于A边，B边和斜边C边的直角三角形， $$$C ^ 2 = A ^ 2 + B ^ 2$ ？ 这是相同类型的连接-见图。 1.对于我们来说，c是恒定速度，正如我们将看到的，它是通用速度极限。 我们还将了解为什么将其称为“光速”。

根据爱因斯坦方程，物体的速度除以速度极限c就是pc与E之比：

$$

$$v / c =（p c）/ E \ qquad（等式2）$$

即，横腿与斜边的比率。 它也等于图2中角度α的正弦。 1.这里是公民。 而且由于直角三角形的边总是短于斜边（任何角度的正弦总是小于或等于1），所以任何物体的速度都不能超过s，即通用速度极限。 随着固定质量物体的速度增加，p和E变得非常大（图2），但是E始终大于pc，因此v始终小于c！


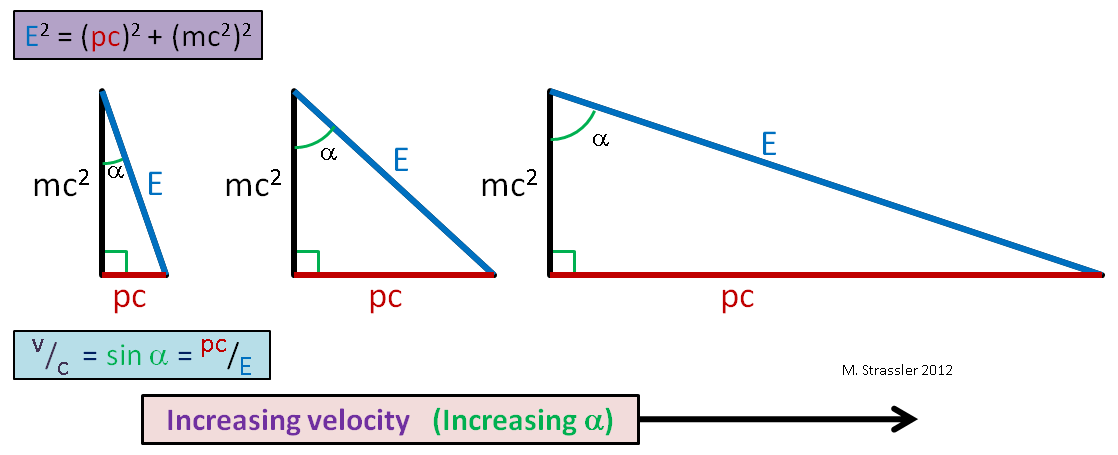图 2

现在请注意，如果对象不移动，则其动量p等于零，并且等式1中的比率减小为：

$$

$$E ^ 2 =（mc ^ 2）^ 2，\ quad或\ quad E = mc ^ 2$$

爱因斯坦著名的公式，即质量与固定能量的关系（我称之为质量能量），是一个简单的陈述，对应于当三角形退化成垂直线时的事实，如图2所示。 左边的3，其斜边的长度与垂直边的长度相同。 同时，这并不意味着能量总是等于质量乘以平方s。 这仅适用于动量为零的静止物体。


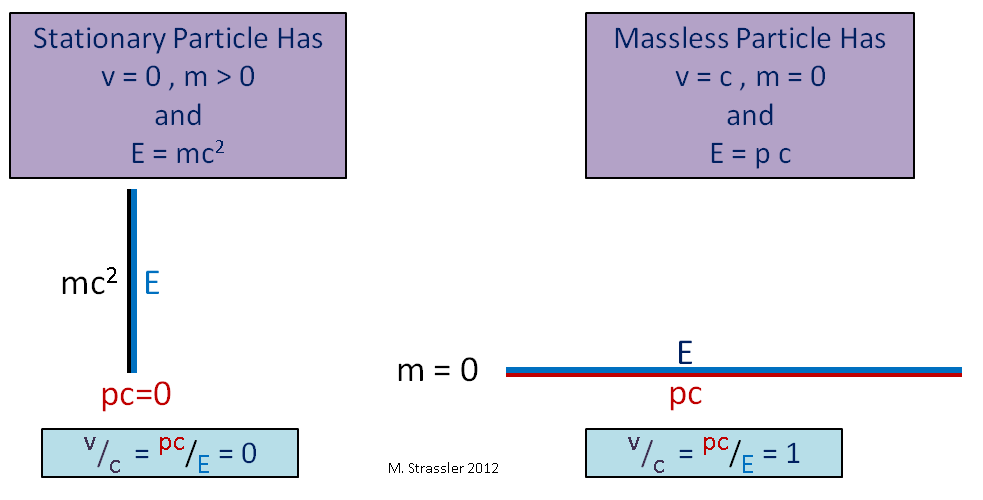图 3

另一个有趣的观察结果：对于无质量粒子，三角形的垂直边为零，斜边和水平边相同，如图2所示。 3.在这种情况下，E为pc，这意味着v / c = 1或v = c。 可以看出，无质量的粒子（例如，光子，光的粒子）不可避免地以c的速度运动。 因此，光速与通用速度限制s相同。

另一方面，如果我们将一个质点定为质点，如图 4，动量和能量有多大无关紧要，E总是比p * c大一点，所以速度总是小于s。 无质量的粒子必须以最大速度传播。 块状粒子的速度应较小。


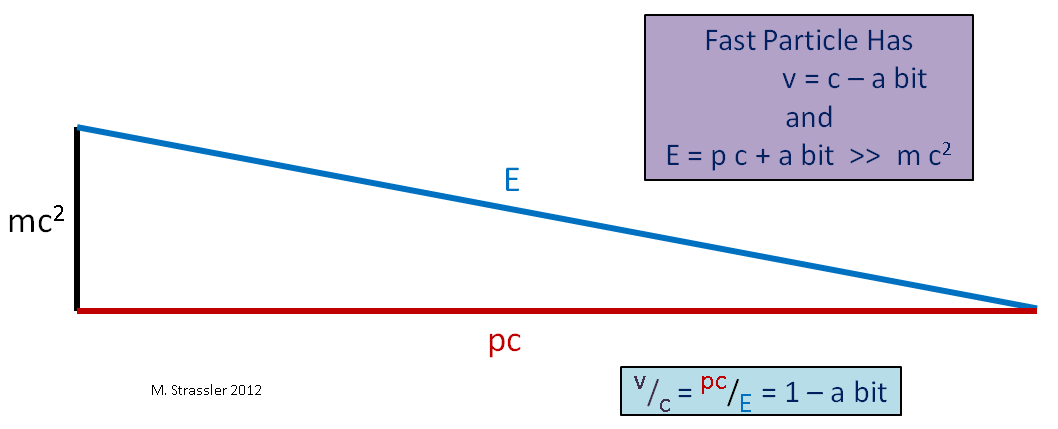图 4.这里的“ >>”表示“更多”

想象另一个临界情况，一个缓慢移动的物体（与光速相比），例如汽车。 由于其速度v远小于c，因此其动量p乘以c将远小于E。 5，E将比mc ²多一点。 因此，慢物体E-mc ²的运动能量远小于其质量mc ²的能量，对于快物体，运动能量可以任意增大，如图2所示。 4。

一个微妙的点：动量不仅是一个数字，而且是一个向量。 他有能力和方向。 它指向粒子的运动。 当我写p时，我仅指示该值。 在许多情况下，有必要跟踪脉冲的方向，尽管在将脉冲与能量和质量相关的等式1中，这不是必需的。


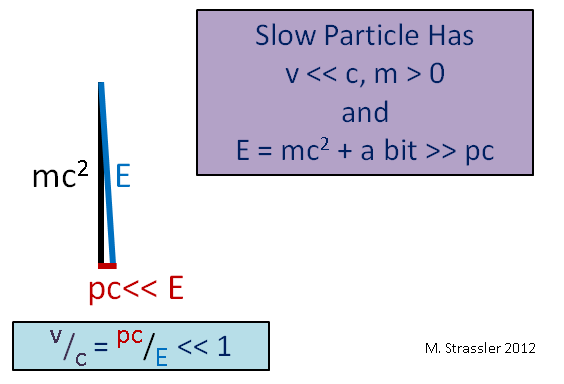图 5

另一个微妙的地方：我使用了三角形和简单的三角函数，因为这是学校里每个人都知道的。 专家需要更加小心-您可以使用双曲线函数正确理解爱因斯坦方程，而双曲函数通常是业余爱好者无法找到的，但是对于理解该理论的结构以及使诸如速度加法，距离压缩之类的事情更容易理解则极为重要。 不装作专家的人可以忽略这一点。

但是速度是相对的吗？

如果您仔细阅读本文，可能已经使您感到惊讶。 您知道粒子的速度-或任何比光慢的速度-都取决于视角。

如果您坐在家里看书，您会说书的速度为零（并且相对于您而言确实是静止的），因此，它没有动量和运动能量，只有质量能量。 但是，如果我站在月球上，我会提醒您地球正在旋转，所以这种旋转使您着迷，并以每小时几百公里的速度使您相对于我移动。 因此，从我的角度来看，您和您的书都会有冲动。

谁是对的？

相对论的变体-伽利略-相对论的第一原理-表明我们都是正确的。 爱因斯坦的相对论变体同意伽利略的观点，两者都是正确的，但是对伽利略的追随者如何表明书的能量，动量和质量进行了重要的调整，将这些量置于方程式1的毕达哥拉斯关系中。

但是，如果一切都正确，我需要用能量/动量/质量的比值替代哪个E和哪个p， $$$E ^ 2 =（p c）^ 2 +（mc ^ 2）^ 2$ ？ 用您看书时测得的E和p代替，即E = mc ²和p = 0？ 还是当您与地球一起移动时，用我的观点来替代本书中的E和p？

这个问题的答案包含了爱因斯坦方程式1的全部实质。 每个观察者将根据该书相对于书本移动的速度来测量该书本的E和p值。 但是对于所有观察者而言 $$$E ^ 2 =（p c）^ 2 +（mc ^ 2）^ 2$ 会是真的！

魔术！ 但实际上，才华横溢的想法是1905年提出的一种想法，即如何用一组令人惊奇的新方程式替换牛顿及其追随者提出的方程组，该方程组仍与之前的所有实验相吻合，但事实证明是对现实的更精确表示。 很难想像，要想出一种思路就必须改变思维方式，直到您弄清楚在新理论形成过程中一切都可能出错的程度，以及有多少其他不同的方程式与数学或先前的实验相矛盾，您才能想象得到。这将是提供（人们提供了它们）。 例如，新手物理学家的工作经常出现在我面前，试图“修正”爱因斯坦的方程，但是我从未见过他们中的任何一个检查其方程的内部一致性。 这是一项非常艰巨的任务，也是大多数理论失败的原因。

但是，如何保存能量和动量呢？

您说，等一下，当您的头部准备好爆炸并让大脑周围的一切飞溅时（我自己也记得这种感觉），但是必须保持精力和动力！ 那么不同的观察者如何才能不同意他们的身份呢？

还有更多的魔力，顺便说一句，这是在爱因斯坦面前。 相信我，宇宙是一个非常非常聪明的会计，尽管事实上不同的观察者不会就一个物体或物体系统中的可用能量达成一致，但他们都同意这种能量不会随着时间而改变。 动量也一样。

但是质量与能量和动量有很大的不同。 首先，质量不守恒。 在自然界中，有许多过程会改变系统的总质量：例如，一个大型希格斯粒子可以衰变成两个无质量的光子。 没有对称性与质量有关，因此Noether对我们没有守恒定律。 其次，与能量和动量不同，能量和动量的值取决于观察者（特别是取决于他相对于被测物体的速度），所有观察者都将同意物体的质量m。 这一点一点都不明显，是因为爱因斯坦方程式非常巧妙地起作用。

那我们有什么

目前，我们乍看之下有几个相互矛盾的知识。 我们知道：

•从任何观察者的角度来看，一个孤立的物理系统的能量和动量都是守恒的（一个孤立的系统的总能量和总动量不会随时间变化）。
•彼此相对移动的不同观察者将以不同的方式评估系统的能量和动量值！
•组成系统的对象的总质量未保存，可以更改。
•但是所有观察者都会同意物体的质量。

此列表还必须添加两个事实和两个结论：

对象物理系统的质量不等于组成该系统的对象质量的总和。

取而代之的是，所有观察者都同意的物理系统的质量由其能量和动量确定，并满足方程式1的形式：

$$

$$(E_{system})^2 = (p_{system} c)^2 + (m_{system} c^2)^2 \qquad ( №1')$$

事实证明，不需要额外的守恒定律，尽管组成系统的物体的质量之和未得到保留，但由于通过方程式1'将其连接到所存储的系统的能量和动量，因此系统的质量得以保留。

对象系统的质量是我们列表中唯一同时被保存且不受观察者辩论的项目。

您只需要记住，对象系统的质量不是组成系统的对象质量的总和，而是方程式1'给出的。

比尝试解释它，只看它如何工作。一个生动的例子值得一千个字。让我们以最时尚的事物为例，即希格斯粒子（质量为126 GeV / s ² ），并查看当上面的各种陈述衰减成两个光子时是如何工作的。

一个希格斯粒子，两个光子和三个观察者

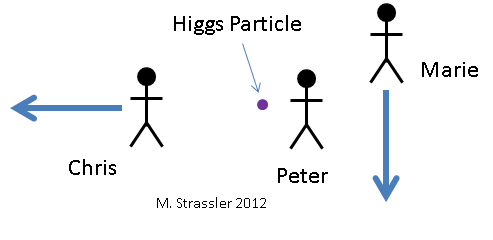图 6.三名观察员观察了希格斯粒子。关于她，彼得（彼得）不动，玛莎（玛丽）下移，科斯蒂娅（克里斯）向左移动。

让我们从三个不同的观察者的角度来看希格斯粒子如何衰变成两个光子。它们如图所示。 6以及他们正在观察的希格斯粒子。当然，他们无法通过眼睛看到她，因为她的时间太短而且太小。他们需要使用某种科学设备。对于Petit，希格斯粒子不会移动。玛莎（Masha）相对于珀蒂（Petit）向下移动。 Kostya相对于Petit向左移动。因此，对于Masha，希格斯粒子向上移动，对于Bone，粒子向右移动。三个观察者根据图2看到粒子如何衰变。 7. Petya看到希格斯衰变为两个能量相同的光子，其中一个向上移动，另一个向下移动。玛莎发现希格斯衰变为两个能量不同的光子，向上移动的能量比向下移动的能量多。Kostya看到希格斯（Higgs）衰减为两个光子，分别向右和向右移动。让我们计算观察者将哪些能量和动量分配给希格斯和两个光子，以及它们各自如何得出在衰变过程中能量和动量守恒的结论。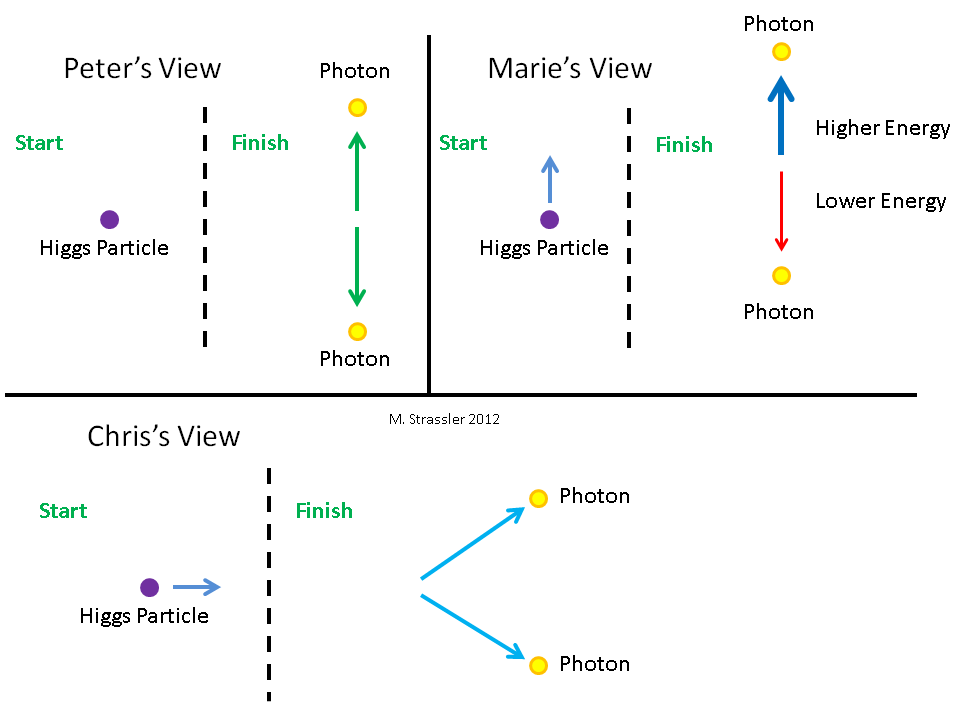

希格斯粒子衰变

首先，我们从Petit的角度分析希格斯粒子。Petya正在（使用测量仪器）看着希格斯粒子，他看到了什么？（我将在Petya看到的所有内容上加一个破折号，然后将其与Masha和Kostya的观察结果进行比较）。希格斯不动，所以他的动力$$$\overline{p_0}$是零，并且根据方程№1它，以其质量m = 126电子伏特/ C²的能量将$$¯ Ë 0 =米c ^2=126Ťë在现在，根据能量和动量，由颗粒组成希格斯的系统的保护，保留所有的能量和衰减后脉冲。直到没有外力影响希格斯时，情况才会如此。您可能会问我们是否需要担心重力，因为重力将是可以改变动量的外部影响。我的回答是，在希格斯衰变的短时间内，引力的影响会很小，以至于如果我告诉你它的确很小，你就会咯咯地笑。算了吧$\overline{E_0} = m c^2 = 126$



因此，当希格斯衰变时，组成其残渣的粒子的能量总计应为126 GeV，粒子的动量（假设动量不仅是数量，而且是方向-向量）都将为零。

希格斯衰变到的两个无质量的光子可以在任何方向上散射，但为简化示例，可以想象它们在垂直方向上散射-一个向上散射，另一个向上散射，向下散射。 （稍后，我们将讨论为什么它们应该朝相反的方向飞行）。

光子有什么动量？很简单首先，系统的总动量-两个光子的矩之和-必须为零，因为希格斯衰变前的动量为零（从Petit的角度来看）。现在，每个光子都有一定幅度和方向的脉冲。总之，如果它们的大小相等且方向相反，它们只能以一种方式给出零。如果一个上升，另一个应该下降，并且它们的大小应该相同。


图 8：佩蒂亚所看到的

第二，系统的总能量是两个光子的能量之和。这是因为它们之间没有相互作用能（除了极小的重力引力，您可能会忘记）。当然，由于它们没有质量，所以它们所有的能量都在运动的能量中。另外，在无质量粒子的情况下，方程式1表示E = pc，其中p是动量。因此，具有相同动量的两个光子必须具有相同的能量。并且由于这两个能量应加起来为希格斯粒子的能量，因此每个光子的能量应等于希格斯粒子的能量的一半。

$$

$$\overline E_1 = \overline E_2 = 1/2 (126 ) = 63$$

由于对于无质量粒子p = E / c，

$$

$$\overline p_1 = 63 /c \uparrow \\ \overline p_2 = 63 /c \downarrow$$

它显示在图。8.

能量和动量守恒，但质量不守恒，因为光子没有质量，希格斯做到了。系统的质量呢？两个光子系统的质量是多少？非零。显然她是什么。以与希格斯本人相同的方式（整个系统最初由希格斯组成），两个光子组成的系统具有与希格斯相同的能量和动量：

$$

$$E_{system} = \overline E_1 + \overline E_2 = 63 + 63 = 126 \\ p_{system} = \overline p_1 \uparrow + \overline p_2 \downarrow = 63 /c \uparrow + 63 /c \downarrow = 0$$

而且因为小 $$$p_{system} = 0$，

$$

$$m_{system} = E_{system} / c^2 = 126 /c^2$$

那就是希格斯质量。如预期的那样，系统质量在衰减期间未发生变化。

希格斯为之向上移动的观察者

玛莎（Masha）相对于佩塔（Peta）往下移动，因此从她的角度来看，佩蒂亚（Petya）和希格斯（Higgs）往上移。假设希格斯以v = 0.8 s的速度移动，即相对于它的光速的4/5。与玛莎不同，从玛莎的角度来看，希格斯具有非零动量，光子的动量在大小上有所不同，但仍是多向的，因此其动量之和将为非零。


图 9：玛莎如何看待希格斯粒子的

衰变从玛莎的角度来看，如何计算希格斯及其衰变成两个光子所具有的动量和能量？为此，我们需要另一组简单的爱因斯坦方程。假设从某个观察者的角度来看，该对象具有动量p和能量E.然后，从另一个观察者的角度来看，该对象以速度v向着对象的方向移动（或与之相反），则对象的动量和能量将表示为：

$$

$$p = γ (\overline p+ v \overline E/c^2) \qquad ( №3) \\ E = γ (\overline E + v \overline p) \qquad ( №4)$$

其中γ满足另一个勾股方程：

$$

$$1 = v^2/c^2 + 1/γ^2 \qquad ( №5)$$

根据爱因斯坦的说法。这使我们能够在Petya所看到的与Masha所看到的（或任何其他以速度v移动的观察者）之间进行转换。我们发现的结果如图2所示。9.

为了将玛莎的观测与佩蒂的观测进行比较，我们需要v和γ。我认为，如果v = 4/5 c，则γ= 5/3。

使用等式5进行检查：1 =（4/5）2 +（3/5）2 = 16/25 + 9/25 = 25/25

佩蒂亚在希格斯说$$$p_0=0, E_0=126$ 。那玛莎呢？她说：

$$

$$p_0 = γ v \overline E_0 = (5/3) (4/5) \overline E_0 = 168 /c \uparrow \\ E_0 = γ \overline E_0 = (5/3) \overline E_0 = 210$$

皮娅声称有两个光子 $$$\overline E_1 = \overline E_2 = 63$，对于每个E = p c。现在，我们可以使用等式4和等式4来计算Masha看到的内容。

$$

$$E_1= γ (1+v) \overline E_1 = 189 , p_1 = E_1/c \uparrow$$

$$

$$E_2= γ (1-v) \overline E_2= 21 , p_2 =E_2/c \downarrow$$

有效！从玛丽的角度来看，能量也是守恒的，因为

$$

$$E_0 = 210 \\ E_1 + E_2 = (189 + 21) = 210$$

冲动也被保存：

$$

$$p_0 = 168 /c \uparrow \\ p_1 + p_2 = 189 /c \uparrow + 21 /c \downarrow = (189 – 21) /c \uparrow = 168 /c \uparrow$$

该系统的质量与衰减前后的希格斯质量一致，因为衰减前后

$$

$$E_system = 210 \\ p_system = 168 /c \uparrow$$

根据等式1'，这使系统的质量回到 $$$126 /c^2$ 像Petit一样，因为

$$

$$210^2 = 168^2 + 126^2$$

从希格斯向右移动的角度来看的观察者

我们对骨头有什么？例如，Kostya相对于Petya向左移动，速度为v = 4/5 s，因此希格斯（和Petya）相对于Kostya向右移动，速度为v = 4/5 s。我们对玛莎所做的相同计算表明希格斯能量$$$E_0 = 210 GeV和p_0 = 168 GeV$ 但是，与希格斯为之向上移动的玛莎不同，对于科斯蒂亚来说，希格斯的冲动指向右边。 如图所示。 10。


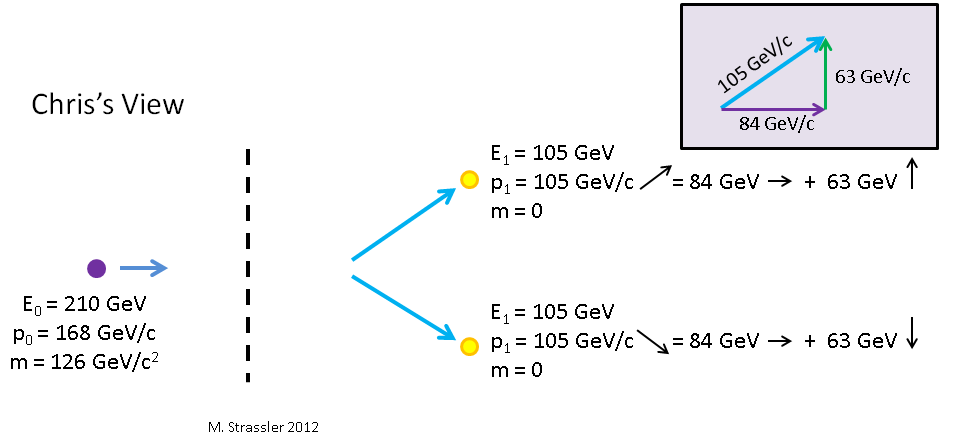
图 10

希格斯衰变为两个光子。 如果从Petya的角度来看，光子是上下移动的，那么对于看着希格斯和Petya向右移动的Kostya，一个光子向右移动，另一个光子向右移动。 他们将拥有什么冲动和能量？

通过方程式4和5，我们不知道这一点，因为它们用于粒子和观察者沿相同方向移动的情况。 对于我们的情况，方程式如下：

$$

$$\ updownarrow p = \ updownarrow \上划线p \\ \ leftrightarrow p =γ（[\ leftrightarrow \ overline p] + v \ overline E / c ^ 2）\\ E =γ（\ overline E + v [\ leftrightarrow \上划线p]）$$

这些方程将比看起来更简单，因为从Petit的角度来看，p没有从左向右移动的分量，并且整个脉冲向上或向下移动。 因此，Kostya会观察到希格斯的以下值：

$$

$$\ updownarrow p_0 = \ updownarrow \上线p_0 = 0 \\ \ leftrightarrow p_0 =γv \上线{E_0} / c ^ 2 =（5/3）（4/5）126 GeV / c = 168 GeV / c \ rightarrow \\ E =γ\ overline {E_0} =（5/3）126 GeV = 210 GeV$$

光子上升

$$

$$\ updownarrow p_0 = \ updownarrow \上线p_1 = 63 GeV / c \ uparrow \\ \ leftrightarrow p_0 =γv \ overline {E_1} =（5/3）（4/5）63 GeV / c = 84 GeV / c \ rightarrow \\ E =γ\上线{E_0} =（5/3）63 GeV = 105 GeV$$

对于第二个光子，公式相同，只是其垂直分量朝下。 注意，对于两个光子，E = pc，根据毕达哥拉斯定理，每个脉冲的大小为p，根据图7中的插图。 10

$$

$$p_1 ^ 2 =（\ uparrow p_1）^ 2 +（\ rightarrow p_1）^ 2 \\或\\（105 GeV / c）^ 2 =（63 GeV / c）^ 2 +（84 GeV / c）^ 2$$

再一次，与Petya和Masha相比，Kostya观察到了其他能量和动量值。 但是对于Kostya而言，能量和动力仍然得以保留。 Kostya还观察到具有两个光子的系统的质量与希格斯质量重合。 怎么了 系统动量的总垂直部分为零，相互抵消。 系统脉冲的水平部分为168 GeV / s。 该系统的总能量为210 GeV。 这与玛莎观察到的一样，只是她的系统动力增强了，而不是向右移动。 但是脉冲的方向不影响方程式1'。 只有它的大小在那里起作用。 因此，就像玛莎一样，科斯蒂亚看到两个质子系统的质量是 $$$126 GeV / c ^ 2$ 等于主要希格斯粒子的质量。

总结

因此，我们看到了三个不同的观察者正在观察。 他们的观察：

•关于希格斯的能量和动量是什么，
•两种光子的能量和动量不同，
•同意衰减过程中能量和动量的守恒，
•因此，他们同意保留系统的质量，
•同意系统质量为126 GeV / c ² ，
•此外，系统对象的质量之和未保留，而是从126 GeV / c ²减小到零。

这不是巧合。 爱因斯坦从以前的实验中知道能量和动量是守恒的，因此他搜索并找到了保留世界这一特征的方程式。 同样在此过程中，他发现系统的质量必须满足方程式1'。

奖励：如何将其用于搜索希格斯粒子

科学家：

•观察质子碰撞，由此产生两个光子；
•计算两个光子系统的质量（用专业术语来说，称为一对光子的不变质量）。

根据实验结果，当希格斯粒子衰变成两个光子时，无论粒子相对于实验室以什么方向和以什么速度移动，其衰变成两个光子的系统将始终具有等于质量的质量。产生它们的希格斯粒子！ 因此，与产生两个质量随机的光子的系统的随机过程不同，希格斯粒子将始终产生两个质量相同的光子的系统。 因此，如果希格斯粒子出现在实验结果中，并且有时它们会衰减成两个光子，那么我们会看到希格斯衰减的峰值超过了其他随机过程所产生的平滑背景。 在大型强子对撞机的实验中也是如此！