数学为我们提供了几乎准确答案的准确图片。

使用厚纸和透明胶带,克雷格·卡普兰(Craig Kaplan)收集了一个漂亮的圆形物体,类似于创建
巴克敏斯特·富勒 (
Buckminster Fuller)或一种时髦的新型足球。 它由四个规则的十二边形(具有相同角度和边的12个角)和十二个十边形(10边的多面体)组成,并具有28个等边三角形形式的小开口。 只有一个问题-这个数字不存在。 这样的一组多边形与顶点不一致,并且图形也不闭合。
之所以能使用Kaplan模型,是因为用纸组装起来时,您几乎没有操纵的自由。 侧面几乎无法察觉地弯曲。 加拿大滑铁卢大学计算机科学家卡普兰说:“由于在现实世界中使用纸张而产生的误差幅度意味着实际上已经获得了不可能的东西。”

这是来自1960年代美国数学家诺曼·约翰逊(Norman Johnson)偶然发现的一类意外数学对象的新示例。 约翰逊(Johnson)致力于完成2000多年前由柏拉图(Plato)开始的项目-他创建了理想几何形状的目录。 在无限多种三维图形中,只能从相同的规则多边形中创建
五个 :四面体,八面体,六面体,二十面体,十二面体。 如果混合使用不同的规则多边形,则可以再组合13个图形,其中所有多边形均会遇到顶点-
阿基米德体 -以及棱镜(两个相同的多边形由正方形连接)和“反棱镜”(两个相同的多边形由等边三角形连接)。
1966年,约翰逊(Johnson)在密歇根大学(University of Michigan)工作时,发现了92个以上仅由规则多边形组成的物体,这些物体现在[在美国]被称为
约翰逊物体 。 这耗尽了所有可能性,几年后,俄罗斯数学家
维克多·阿布拉莫维奇·扎加勒 (
Viktor Abramovich Zalgaller )证明了这一点,后来他在列宁格勒州立大学工作。 无法从规则多边形制作任何其他闭合形状。
但是在盘点多面体时,约翰逊注意到了一些奇怪的东西。 他找到了自己的造型,并用硬纸板和橡皮筋组成了模型。 由于几乎没有多面体,因此他希望新形式会很快出现。 如果您开始一起做鬼脸,那么这个数字必须是一致的。 但这没有发生。 约翰逊回忆说:“当组装一堆多边形时,并不总是很清楚我是否组装了有效的形状。”
他说,似乎模型已经组装好了,但是“如果进行计算,事实并非完全如此。” 经过仔细检查,结果似乎是一个正方形不是一个正方形,或者侧面不是很平坦。 可以略微修剪这些面,它们将非常适合,但随后它们将不再是规则的多边形。
为了计算所有理想的数字,约翰逊并不重视这种“近距离命中”。 他说:“我把它们放在一边,专注于可以接受的东西。” 但是这些几乎理想的人物不仅吸引了卡普兰和其他数学爱好者的注意,而且成为了更大一部分理想数学的一部分。
没有“几乎准确”的匹配的确切定义。 严格的规则在宽容的世界中行不通。 现在,卡普兰在寻找几乎正确的图形时采用了一种近似方法:“图形中固有的真实的数学错误可与处理真实材料和不完美的手所产生的实际错误相提并论。” 换句话说,如果您设法组装了一个不可能的多面体-如果它非常接近以至于您可以将其作为一个真实的多面体进行传递-那么这将是几乎准确的数字。 在数学的其他分支中,几乎准确的结果非常接近真实,以至于它们可以欺骗或使您感到惊讶-这是一种数学笑话。
这些数学上的奇异事物中,有一些仅是简单的乐趣而已,而另一些则在数学和物理学中具有深远的意义。
平方圆和
加倍立方体的古老问题属于几乎正确的解决方案。 他们似乎很想找到正确的解决方案,但最终却发现这是不可能的-就像看起来很封闭但不是的几何图形。 莱昂纳多·达·芬奇和阿尔布雷希特·杜勒绘制的一些设计略微弯曲了角落,散发出几乎是真实的五边形。
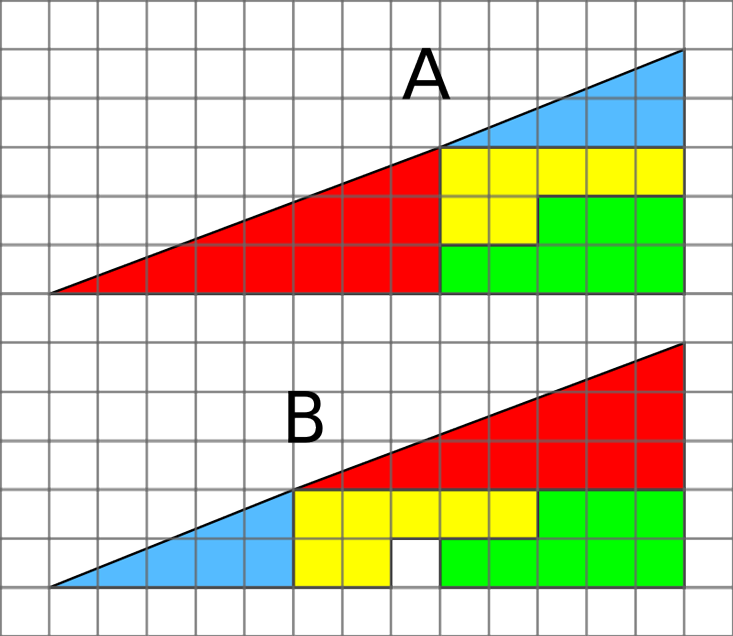
还有一个谜语,其中缺少一个方块。 在该图中,直角三角形被切成四个部分。 如果重新排列它们,则会在其中出现间隙。 他来自哪里? 这几乎也是正确的决定。 三角形实际上都不是三角形。 他们的斜边是扭曲的,几乎不可能注意到,这就是为什么这种错觉如此令人信服的原因。
数字匹配是日常生活中最有用的近乎正确的决定之一。 2
7/12几乎等于3/2。 出于类似的原因,钢琴在八度音阶中还有十二个键,位于西方音乐
平均调律系统的核心。 这是两个最重要的音乐间隔之间的折衷:一个八度(频率2:1)和第五(频率3:2)。 从数值上讲,不可能将八度音阶除以使所有五分之一都是完美的。 但是您可以通过将八度音阶划分为12个半音来获得足够的效果,其中七个音阶的频率为1.498。 对于大多数人来说,这就足够了。
有时,几乎是精确的命中出现在数学中,就像在欺骗自己一样。 在辛普森一家情节“恐怖的树屋”中,对数学感兴趣的观众注意到了一些不寻常的东西:方程式1782
12 + 1841
12 = 1922
12 。 乍看起来,作者似乎反驳了费马大定理,该定理假设x
n + y
n = z
n的方程没有n> 2的整数解。如果将这些数字输入到袖珍计算器中,结果似乎是正确的。 但是,如果您使用大多数袖珍计算器无法获得准确的计算结果,结果发现,方程式左侧12度的根是1921,999999955867,而不是1922,Fermat可以保持冷静。 出乎意料的小滑差-少于1000万个零件。
但是,如此接近准确的点击率不只是笑话。 加州大学里弗赛德分校的数学家约翰·贝兹(John Baez)说:“那些比其他人更吸引我的案例暗示着更重要的事物的存在。” 有时称为
Ramanujan常数的数量就是这种情况。 该
eπ163数大约等于262537412412640768 743.9999999999999925,令人惊讶地接近整体。 我们不能指望这三个无理数-e,π和√163-将以某种方式组合并给出一个有理数,更不用说整体了。 但是有一个很好的匹配的原因。 贝兹说:“我们不知道这不仅仅是巧合,” “这是深入数学的关键。” 确切的解释相当复杂,但是基于163是
Hegner数最大的事实。 与这些数字相关的参展商非常接近整数。
或采用数学上称为“怪异月光假说”(怪异月光假说)的联系。 故事是这样的:1978年,数学家约翰·麦凯(John Mackay)进行了微不足道的观察:196 884 = 196 883 +1。第一个数字是一个重要多项式的系数
j不变式 ,第二个数字是与群论中一个巨大的数学对象有关的叫做“
怪物 ”。 许多人会耸耸肩膀并走得更远,但是这种观察吸引了许多决定进一步研究它的数学家的兴趣。 他们发现了两个看似无关的话题之间的联系:数论和怪兽群体的对称性。 这种联系可能会对其他主题产生更大的影响,但尚未开放。 物理学家爱德华·惠顿(Edward Whitten)认为,Monster组可以与量子引力和时空结构相关联。
数学上几乎正确的命中既显示了趣味性,又显示了人类数学方法的力量。 约翰逊(Johnson),卡普兰(Kaplan)等人通过反复试验获得了发现-作为生物学家在丛林中跋涉寻找新物种的研究领域。 但是在数学中,进行系统的搜索会更容易。 例如,吉姆·麦克尼尔(Jim McNeill)对数学很感兴趣,他的爱好是数学,并在其网站上收集了几乎正确的匹配数据;程序员罗伯特·韦伯(Robert Webb)则创建了用于创建和研究多面体的软件。
在理想主义,苛刻的数学与我们谦逊的和实际的感觉之间的模糊界限上,几乎是准确的命中词。 他们证明了近似逻辑。 通常,现实世界被认为是柏拉图世界的不完美阴影。 基础数学的完美性在其实施中丢失了。 但是在命中率几乎准确的情况下,现实世界是不完美世界的完美阴影。 近似值是“正确答案的错误近似值,” Kaplan说,“几乎准确的命中是几乎准确答案的准确表示。”
这样,几乎准确的答案改变了数学家和数学物理学家与自然之间的联系。 卡普兰说:“我感谢现实世界的不完美,因为它们使我能够通过与本质上不完美的物体一起工作来达到准理想状态。” “由于残缺的现实之美,它们使我克服了数学的局限性。”