我们了解粒子物理学：1）弹簧上的球，牛顿版

1. 牛顿弹簧上的球
2. 弹簧上的量子球
3. 波浪，经典外观
4. 波浪，经典的运动方程
5. 量子波
6. 领域
7. 粒子是量子
8. 粒子如何与场相互作用

通俗地理解粒子物理学的基础-这是我们目前对宇宙中大多数基本现象的理解-并不是那么困难。 如果您就读物理和数学学校或完成大学一年级课程，对您来说会更容易。 但是，如果您处理代数，三角学以及（可能但不一定）处理微分和积分的基础知识，那么您可以了解场的工作方式以及粒子的外观。 关于量子力学的一个方面，您只需要一听即可。 在那种情况下，我不会给出数学公式，而只是向您显示现成的答案。 但是在您接受了这方面之后，其他所有内容都将变得清晰。


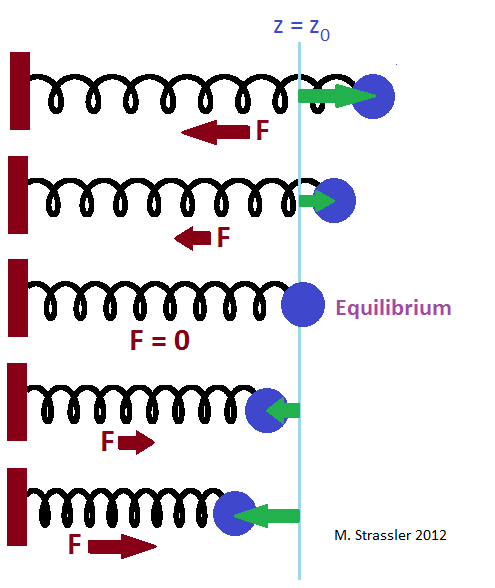图 1个

要了解粒子物理学，从学校物理学开始，您需要记住一件事-弹簧是如何工作的。 实际上，反弹，振动，响起，发出嘎嘎声，来回摇晃的一切都是春天的例子。

想象一下，我们在弹簧的末端放了一个球。 弹簧的运动和描述它的方程很简单。 首先，我们回顾一下弹簧行为的基础知识，然后研究球的行为-振荡。 最后，对于最好奇的人，我们将考虑导致这种运动的方程式。

谐波振荡器（又称弹簧上的球）

弹簧上的球具有平衡位置； 如果将球放进去然后释放，弹簧将不会向任何方向推动，并且球将保持静止。 这是图中的蓝线。 1.如果将球从平衡位置拉开（绿色箭头），则弹簧将以力F将球向后拉（红色箭头）。 将球拉得越远，弹簧向后拉的力就越大（至少直到您将弹簧折断或用压力将其折断为止）。

摆动运动（跳跃）

我们将球的运动方向称为“ z方向”，并定义z轴，以使z = z ₀对应于球在弹簧上的平衡位置。 假设我们从该位置拉动球，并握住球使其不移动到位置z = z ₀ + A; 然后，在某个时间点t = 0，我们将其释放。 球将开始在这里和那里跳-见图。 2.跳跃的幅度-振荡的幅度-等于A。它可以任意大或小； 只有您选择从平衡位置拉球的量。 但是，您无法控制来回跳跃的频率（振荡频率ν）的发生频率。 不管A的值如何，结果都是一样的。它仅由球和弹簧的特性决定，而不由您的工作决定。

出于科学目的，通过数学公式描述观测值极为重要。 球z的位置是时间t的函数，我们写为z（t），形式为：

$$

$$z（t）= z_0 + A cos [2 \ pi \ nu t]$$

通常，cos是余弦，π是圆的几何形状中的数字pi，z ₀是球的平衡位置，A和ν（nu）是振荡的振幅和频率。 余弦函数具有振荡性，因此该公式描述了振幅为A，频率为ν的振荡运动。 图中显示了具有不同初始偏差值和总振幅A的弹簧上的球的振荡运动的示例。 如图2所示，该图还显示出对于弹簧上的给定球，频率ν不依赖于振幅A。

精细打印：幅度和频率大于零。 如果A为负，则幅度将为–A。 实际上，振幅实际上是| A |，即振幅模量。


图 2

关于球和弹簧的振幅和频率（在经典的量子前物理学中），要记住非常重要的一点：
•幅度A可以选择任何一个；
•频率ν由球和弹簧决定，要选择不同的频率，必须更换弹簧或球。

每次振荡的周期（准确地向前和向后移动一次球需要多长时间）将称为T，而该周期仅是频率的倒数：T = 1 /ν。 如果周期为5秒，则频率为每5秒一次或1/5秒（通常称为1/5赫兹或Hz）。

另一个小字样：在日常生活中遇到的任何弹簧和球的真实系统中，摩擦都会导致这样的事实，即A会逐渐减小并最终在运动停止时达到零。 考虑到运动过程中的摩擦的公式并不复杂，但是我们将不需要它们。 因此，我总是假设摩擦很小，A的减小非常缓慢，我们可以简单地使用忽略摩擦的简化公式。 但重要的是要知道：摩擦力会减小A，但是除非它非常强，否则它不会影响ν和T！ 即使幅度减小，振荡频率也保持不变。 因此，拉动吉他弦后产生的音符不会改变，即使所产生的声音逐渐消失。

还有一件事：在振荡的弹簧中存储能量的公式很漂亮。 它与幅度的平方和频率的平方成比例：

$$

$$E = 2 \ pi ^ 2 \ nu ^ 2 A ^ 2 M$$

这部分是球的运动能量（动能），部分是弹簧中存储的相互作用能（势能），当球来回摆动时，这些能量在总能量中所占的比例不断变化。 但是总能量E保持恒定。

缩略语：仍然有球质量Mc ²的能量，但是我们不追踪它，因为它始终在其中，弹簧是否随其移动。

相同的振荡公式几乎适用于所有颤抖或跳跃的事物，只要这些跳跃不是太大。 球沿着碗的底部滚动； 一辆跳着不良减震器的汽车； 小提琴或吉他的振动弦； 击打后的木琴横条； 等

振动运动方程（数学跳）

现在，让我们回想一下基本公式，这些基本公式向我们解释了为什么弹簧上的球会振荡。

正如我们在一开始提到的（图1），弹簧上的球具有一个平衡位置，我们称其为z = z ₀ 。 假设在某个时间点（我们将球拉出或犹豫了），它处于不同的位置z。 如果z> z ₀ ，也就是说，如果从平衡位置z-z ₀的位移大于零，那么弹簧将产生一个沿负方向z的力将球拉回到平衡点。 相反，如果z <z ₀ ，即从平衡z-z ₀的位移_为负，则弹簧将产生一个沿正方向z的力，再次将球拉回到平衡点。 球离平衡位置越远，弹簧拉力就越大。 弹簧产生的力F与球的平衡位移有关，方程如下：

$$

$$F =-K（z-z_0）$$

其中K是一个正值，取决于特定的弹簧，称为弹簧常数。

注意为什么这个公式是正确的：

•如果球处于平衡位置，则F =0。弹簧不会产生力，如果球没有在平衡位置移动，它将保持在那里。
•如果偏差大于零，则力为负。
•如果偏差为负，则力为正。
•偏差越大，强度越大。

然后我们转向牛顿第二运动定律，该定律指出，在力F的作用下，质量为M的球将以加速度a移动，其中F = M a。 将其替换为公式并得到

$$

$$M a =-K（z-z_0）$$

或

$$

$$a =-K / M（z-z_0）$$

对于我们来说，这是几乎必要的方程式，从中可以得出振动方程式。 我们只需要回忆一下a和z之间的关系。 为此，重要的是回忆一下a与速度v之间以及v与z之间的关系。 该比率是随时间变化的两个值之一：
•速度是时间位置的变化，v = dz / dt
•加速度是速度随时间的变化，a = dv / dt

添加并获取

$$

$$a = d（dz / dt）/ dt = d ^ 2z / dt ^ 2$$

加速度是位置随时间变化的时间变化。

我们可以重写运动方程

$$

$$d ^ 2z / dt ^ 2 =-K / M（z-z_0）\ quad（*）$$

其中z是z（t）的缩写。 现在我们可以验证振动运动z（t）= z ₀ + A cos [2πνt]将是该运动方程的解。 我们首先需要计算粒子的速度作为其位置随时间的变化：

$$

$$d / dt（z_0 + A cos [2 \ pi \ nu t]）=-（2 \ pi \ nu）A sin [2 \ pi \ nu t]$$

（dz ₀ / dt = 0，因为平衡位置z ₀不会随时间变化，并且d / dt（cos wt）= -w sin wt）； 然后我们将粒子的加速度计算为粒子的速度随时间的变化：

$$

$$d / dt [-（2 \ pi \ nu t）] =-（2 \ pi \ nu）^ 2 A cos [2 \ pi \ nu t]$$

（因为d / dt（sin wt）= w cos wt）。 结果

$$

$$d ^ 2z / dt ^ 2 =-（2 \ pi \ nu）^ 2 A cos [2 \ pi \ nu t] =-（2 \ pi \ nu）^ 2（z-z_0）$$

在最后一步中，我使用公式z（t）= z ₀ + A cos [2πv t]进行振荡运动。 最终方程与我们的运动方程相同[ $$$d ^ 2z / dt ^ 2 =-K / M（z-z_0）$]，假设（2πν） ² = K / M，如果振荡频率为

$$

$$ν= \ frac {\ sqrt {K / M}} {2 \ pi}$$

而且，实际上，我们发现运动方程式表明弹簧将以指定的频率振荡，该频率不取决于A-它仅取决于弹簧（K）和球（M）的特性-并且无论对于方程式的数量A，有一个解。 因此，我们可以选择任意一个A，具体取决于在释放球之前将球从平衡位置拉出多远。

共鸣

共振是最重要的自然现象之一，无论是在普通生活中，在技术和音乐的许多方面，还是在物理世界的基本过程中，特别是在粒子物理学中，它都发挥着作用。

首先，请记住秋千的工作原理。 摆动（如弹簧上的球或任何摆锤）是一个振荡器，它以一定的频率来回摆动，该频率不取决于摆动幅度。 在摆动的情况下，该陈述将保持正确，直到振幅非常大为止。 您可能从经验中知道，要使孩子摆动得更高，您需要每个周期向前推动一次摆动，以使摆动幅度不断增加。 如果在每个周期中将摆动向前推动几次，或者每两个半周期将其向前推动一次，则有时会增加摆动幅度，有时会减小幅度。 显然，将挥杆的频率与挥杆本身的固有频率对齐是有一些特殊之处的。

类似地，如果孩子本人知道如何摆动秋千，则他知道他需要与摆动的自然频率同时摆动双腿，以增加摆动幅度。 以不同的方式摆动，振幅不会增加。



您可以追踪弹簧上的球如何发生。 看图片。 左边是一个在平衡位置上来回摆动的球。 他犹豫不决，没有外界的冲击。 它以弹簧ν的固有频率振荡。 频率为√K / M，其中K为弹力，M为球的质量。

在图的右边。 您可以看到在同一弹簧上另一个质量等于第一个黑色球的情况，该球被力F（其大小和方向由红色箭头显示）推动，其振动频率νF与ν不同。 黑色的球就像挥杆一样，很少被推动。 它们将以复杂的方式运动，并且不会爬高。 在图。 可以看出，球不很平稳地振荡，并且振荡的幅度很小。 您可以看到他如何“试着”以自然频率振荡，尽管他的一般动作以频率νF重复_。

然后该图显示了一种情况，其中力以频率νF振荡，该频率远高于频率ν。 再次，您可以看到他如何“尝试”以自然频率振荡，但是他并没有成功完成大幅度的振荡，因为快速振荡的力既可以推动其自然运动，也可以使其反向运动，从而增大或减小幅度。

最后，显示了当力以弹簧的固有频率νF =ν振荡时的情况。 球的反应截然不同：振荡的幅度不断增加，黑球的振荡与左侧的白球一样容易且平稳，但振幅增加。 这是一种共鸣。

结果是：如果νF与ν不同-如果力不允许球进入共振-它将移动，但很不情愿，并且它的运动与自然振动非常不同，其频率为ν。 相反，如果力的频率与自然频率相对应-如果力将球引入共振状态，则该力会更有效地推动球，从而产生更大的运动感。 我们凭直觉知道这一点； 孩子（或父母）以自然的频率推动秋千时，秋千会越来越高。

粒子物理学中共振的重要方面之一是，在某些情况下，由于非常相似的机制而可以生成粒子的事实：两个粒子碰撞后，所获得的力与产生第三个粒子所需的频率完全相同。

下一次：弹簧上的量子球

这是经典的量子前物理学中的弹簧上的球的行为。 量子力学改变了许多概念 ，但是最重要的是：我们仍然可以选择A，但是A不能有任何大小。 它只能采用与整数的平方根成比例的某些值。