我们了解粒子物理学：3）波，经典形式

1. 牛顿弹簧上的球
2. 弹簧上的量子球
3. 波浪，经典外观
4. 波浪，经典的运动方程
5. 量子波
6. 领域
7. 粒子是量子
8. 粒子如何与场相互作用

处理了振动方程后，几乎像弹簧上的球一样，描述了所有跳跃，振动，来回滚动的事物，我们可以继续研究同样普遍的自然现象，即波浪。 海浪无处不在：声光，地震，池塘表面的涟漪等。


图 1个

但是在此之前，我警告您，“波”一词可能会引起误解，因为在物理学中，它与英语中的含义不同。 在物理学中，这并不意味着我们通常将其称为海洋边缘的波-一个波峰和一个空洞。 在物理学中，波是一系列波，沿相同方向一起移动的多个脊和谷。 在最简单的形式中，所有的脊都具有相同的高度，并且彼此间隔一距离。 我们将考虑这种情况。

如果您考虑一下，波浪是一种杰出的现象。 想象一下，您和您的朋友用一根长绳将其拉紧在房间里（图2）。 然后想象一下，您的朋友用绳子的一端（绿色）上下聊天了几次。 波浪将出现在绳索的末端，它将穿过房间到达绳索的末端（红色）。


图 2

太神奇了 我的意思是-对于我们整个宇宙，包括您个人在内，这都是令人惊奇，强大和至关重要的。 看发生了什么事。 没有任何物理对象从左向右移动-在您的朋友开始移动绳子的末端之前，绳子一直延伸到整个房间，最后，在您的绳子的末端停止振动并且波消失之后，绳子仍会在整个范围内延伸房间，照原样。 还没有！ 能量和信息在房间中移动。 途中的波浪将您的朋友花费在绳子振动上的能量传递给您，并在其中传递有关其拉动次数和速度的信息，使您握手。 在这种情况下，她甚至会按此顺序多次握手。 哇！ 没有一个物理物体在房间中移动，能量和信息也没有移动。

还是等一下。 但是我们不应该将波浪视为物理对象吗？ 像绳子本身一样物理？

记住这个最深层的问题，我们转向描述波的外观和行为所需的少量数学公式，然后使用更多的数学来写下以波为解的方程。 这类似于我们对经典弹簧球所做的操作。

特定时间点的无限波公式

此系列文章紧接在弹簧上的球向波浪移动时，因为波浪是一种双振动器。 它随时间和空间波动。 我们用字母“ t”指定时间，用“ x”表示空格。

注意图。 3.它描绘了一个在两个方向上延伸很长距离的波，在该波上有许多山脊和凹陷。 这与图2中的波形不同。 2，它只有几个脊和凹陷。 但是这种差异是无关紧要的-在图2中。 2我需要说明确切的波形无关紧要； 现在，我们将集中讨论波浪的数学公式，如果波浪具有大量相同大小的山脊和凹陷，则操作起来会容易得多。 同样，这种情况对于证明量子力学如何影响波的行为将是非常有用的。



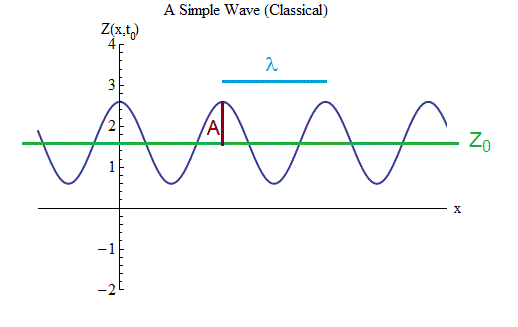
图 3

首先，我们需要确定表示法，并在图1中写下描述运动和波形的公式。 3，像我们在春季做球一样。

该图显示了在特定时间段t = t ₀中波Z的大小与空间的关系-我们将其记录为Z（x，t ₀ ）。 跟踪空间中的波，我们看到它向前和向后振荡，Z周期性地增加和减少。 在任何时候，波都会在空间中振荡。

注意，Z不必与物理距离有关。 如图所示，它可以是绳索的高度。 在图2中，它可以是完全不同的东西，例如，在空间和时间上的某个点处的空气温度或在磁体的某个位置中的磁性原子的取向。 但是x仍然代表物理距离，而t是时间。

Z（x，t ₀ ）表示该波具有三个有趣的特性，其中两个也适用于弹簧上的球。

1.在脊上的最大Z值与凹陷处的最小Z值之间的中间位置有一个平衡值Z ₀ 。 大多数时候，我们研究Z ₀ = 0的波，因为值Z ₀通常并不重要-但并非总是如此。
2.波的振幅为A，即Z值从平衡值变化到每个波峰的顶部，或以相同的值变化到每个凹陷的底部的值。
3.波浪的长度为-相邻脊之间的距离λ，或者相邻槽之间的距离λ，或者相同，是相邻脊和槽之间的距离的两倍。 它以与周期（等于1 /频率）描述弹簧上球的时间振动相同的方式描述空间振动。


图 4

让我们想起图2中的表格。 3？ 它看起来像一个正弦或余弦函数的图形-见图。 4，其中cos（w）绘制在w上。 Cos（w）是一个振荡函数，在零处有一个明显的平衡位置，其振幅为1，波长为2π。 如何从无花果。 图4为波的公式。 3？ 首先，我们将cos（w）乘以A，以使振幅等于A。然后将Z ₀加到整个公式中，以将其移动到所需的平衡值（如果A = 0，则没有振荡，并且一切都停留在点Z = Z ₀ ）。 最后，将w替换为2πx/λ，因为cos（w）的脊在w = 0且w = 2π，因此，在cos（2πx/λ）时，脊将在x = 0且x =λ。 在一起给我们

$$

$$Z（x，t_0）= Z_0 + A cos（2 \ pi x / \ lambda）$$

这几乎与描述球在弹簧上的运动的公式相同：

$$

$$z（t）= z_0 + A cos（2 \ pi \ nu t）= z_0 + A cos（2 \ pi t / T）$$

其中ν是振荡频率，T = 1 /ν是振荡周期。 参见类比：周期是指时间，波长是指空间。

在继续之前，请多加注意。 我也可以写：

$$

$$Z（x，t_0）= Z_0 + A cos（-2 \ pi x / \ lambda）$$

由于cos [w] = cos [-w]。 我们很容易在波形公式中替换负号，这一事实在稍后将变得很重要。

在特定位置产生无尽波浪的公式

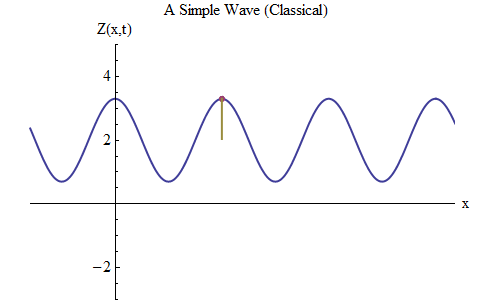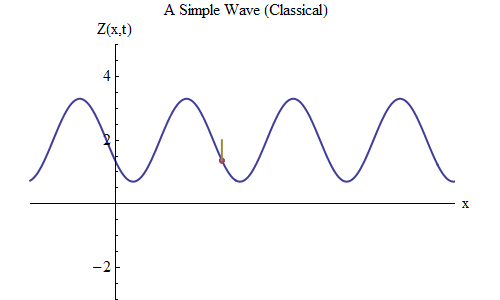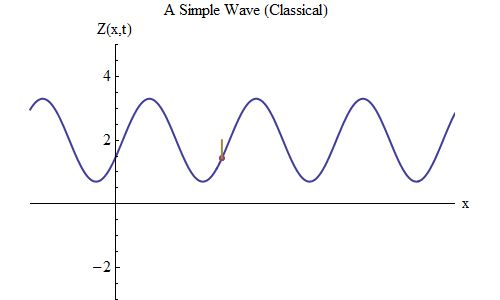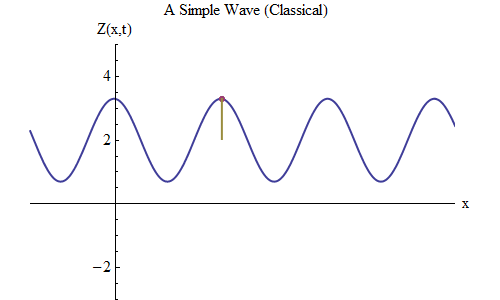图 5

现在让我们问另一个问题：让我们看看波浪如何随时间变化，跟踪绳索上的某个点，以及它的行为和运动方式。 如图所示。 5：我指定了一个特定点x ₀ ，在时间t ₀处在波峰上。 波向右移动并在点x ₀处跟随波Z的大小，随时间变化：Z（x ₀ ，t）。 您将立即看到在特定点处的波高表现得就像弹簧上的球一样！ 因此，它具有与弹簧上的球完全相同的公式，取决于频率ν或周期T = 1 /ν，其中T是x ₀处的波到达波峰的那一刻与到达波峰的那一刻之间的时间。下次她再次接近波峰。

$$

$$Z（x_0，t）= Z_0 + A cos（2 \ pi \ nu t）= Z_0 + A cos（2 \ pi t / T）$$

完整的无限波公式

现在我们需要一个Z（x，t）的公式来描述图2中所示的波。 在任何时间t的点x上的3和5（或任何类似的一个）。 正确答案是：

$$

$$Z（x，t）= Z_0 + A cos（2 \ pi [\ nu t-x / \ lambda]）= Z_0 + A cos（2 \ pi [t / T-x / \ lambda]）$$

它既包含固定时间点的公式，又包含空间固定点的公式。

请注意x前面的减号。 我提到过，在Z（x，t ₀ ）的公式中，您可以随意替换负号。 在x前面有一个负号，在t前面有一个加号，该公式描述了一个向右移动的波浪，如动画所示。 为了验证这一点，请注意，当t / T-x /λ= 0时，该波将是波峰，因为cos [0] = 1。 当t = 0时，在点x = 0处是脊。 但是，如果我们将t向前移动一点，例如T / 10，那么波峰将位于x =λ/ 10处，即t = 0处的右侧-因此波峰（以及整个波浪）向右移动。

如果在Z（x，t）的公式中放置加号而不是减号，将会发生什么变化？ 然后，波峰将位于t / T + x /λ= 0，在这种情况下，波峰将位于t = T / 10处，波峰将位于x =-λ/ 10，位于t = 0处的左侧-这意味着，现在波向左移动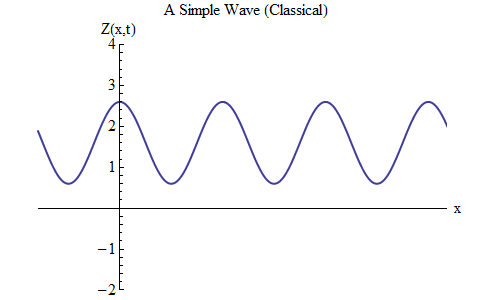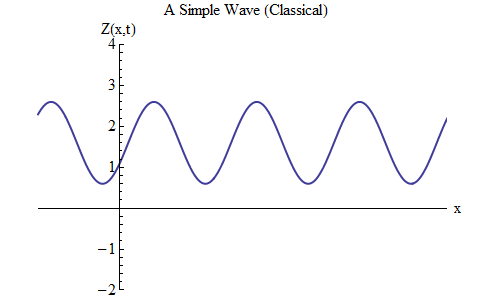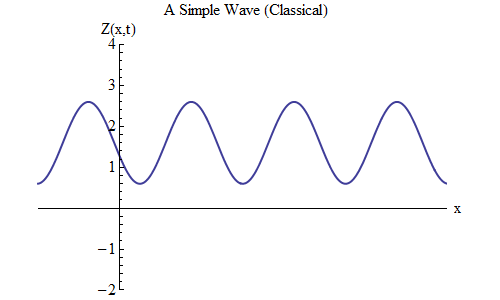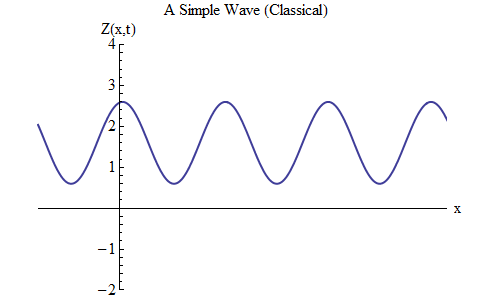（图6）。


图 6

作为x和t的函数的波可以在任何方向上移动，因此我们只需要为给定的波选择正确的公式即可。 一般而言，当我们处理的波不仅可以沿一个空间维度x移动，还可以沿所有三个坐标x，y和z移动时，这些波可以沿任何方向移动，因此我们需要根据方向选择正确的公式波动。

精美的字样：我们可以在t前面加上减号，而不要在x前面加减号。 但是+ t，+ x与–t，-x相同，因为它等效于将余弦中的整个公式乘以-1，并且cos [w] = cos [-w]。 因此，+ t，+ x和-t，-x会使波向左移动，而+ t，-x和-t，+ x会使波向右移动。

波动方程

现在，就像弹簧上的球一样，当我们首先找到球的振荡运动的公式，然后查看运动方程式（对于该方程式是解决方案）时，我们将在此处进行操作。 我们找到了波浪形状和运动的公式。 解决方案中的哪个运动方程式具有这样的公式？ 我们将在下一篇文章中学习。