1.
牛顿弹簧上的球2.
弹簧上的量子球3.
波浪,经典外观4.
波浪,经典的运动方程5.
量子波6.
领域7.
粒子是量子8.
粒子如何与场相互作用实际上,我们前段时间进入了野外领域,我只是没有警告您-我想专注于这些领域中产生的海浪。 描述波的行为时,我们使用函数Z(x,t)表示了它们的形状和对时间的依赖性。 Z(x,t)是一个字段。 这是时空的函数,其运动方程式决定了其行为。 合适的运动函数应为:如果Z在某个点增加或减少,则Z将在稍晚一点在相邻点减少或增加。 此功能使波成为方程式的解。
在本文中,我们将介绍Z(x,t)场的一些示例,这些示例的运动方程式允许存在波。 这些字段的物理解释将有很大不同。 他们描述了不同材料的不同特性。 但是,尽管它们的物理起源不同,但它们满足的方程式和所展示的波动将满足非常相似的数学,并且它们的行为类似。 这将是将来非常重要的一点。
然后我们做一些激进的事情-在相对论的特殊背景下考虑这些领域。 正如爱因斯坦所表明的那样,如果您纠正空间和时间并强迫它们以大多数人所期望的方式去领导,那么您将获得一种新型的场-从而其物理解释不是任何其他事物的属性,而是一个独立的物理对象。
描述普通事物的普通字段
场Z(x,t)可以表示许多不同的物理量。 例如:
•绳索的高度延伸到整个房间。
•河水的高度。
•晶体或气体的密度。
•原子在磁体中的位置。
•风速。
•温度,密度或气压。
在任何一种情况下,都会有一个Z(x,t)字段:高度字段,密度字段,方向字段,风场和温度字段。 它的值是时空函数,它告诉我们在任何给定时间在任何地方的某种介质(绳索,河流,水晶,气体,磁铁,空气)的高度,密度,方向,风速或温度。 他的运动方程式说明了Z(x,t)在原理上如何表现。 如果我们确切知道Z(x,t)在现在和过去的行为,它还显示了如何预测Z(x,t)在将来的行为。
在每个示例中,都有一个字段和环境,我们不应将字段与环境混淆。 该字段仅描述和表征相应环境的许多属性之一。 完全不同的环境可能具有非常相似的行为场和非常相似的波-我们仍然会看到它。
我将再次澄清一个经常引起误解的观点。 通常,一个场可能与空间中的物理距离无关。 是的,在第3条和第4条中,我以绳索上的黄牛为例来说明Z(x,t)可以是什么,因为它美观且直观。 我还经常绘制波的Z(x,t)图。 这可能会给您带来错误的印象,即Z(x,t)总是与导致物理对象(例如绳索)在垂直于x轴的方向上移动距离Z的波相关联。 但是事实并非如此,因为我们四个示例中的三个将向我们展示。
绳高场
首先,考虑波动的最初示例,即振荡绳。 在这种情况下,Z(x,t)的作用是高度场,我们称之为H(x,t)。 它告诉我们在任何时间t处沿绳索在x轴上的每个空间点处绳索的高度。 如果绳索处于平衡高度H
0 ,则H(x,t)= H
0 。 高度场在时间和空间上是一个常数。 如果有简单的波浪通过,那么高度场将由我们先前文章中著名的波浪公式来描述。
如果我们知道H(x,t),那么我们就知道了在空间和时间的所有点上绳索的高度。 如果我们知道绳索现在在做什么以及最近在做什么,则使用运动方程式,我们可以预测绳索将来会做什么。 这几乎没有告诉我们绳索本身。 高度字段仅给出他的名字所暗示的含义:绳索的高度。 绳索是一种物理介质,其高度表示为场H(x,t); 它没有告诉我们有关绳索的颜色,厚度,张力,材料等的任何信息。
在图。 1我为您制作了一个高度场中从左到右的波浪动画。 似乎我曾两次涂过相同的东西,首先是绿色,然后是橙色。 但这不是同一回事。 橙色曲线是绳索本身,在物理空间中移动。 绿色曲线是表示H(x,t)发生了什么的图形,而与H(x,t)(即高度)的含义或环境无关。 而且只有在这种情况下,绿色图形看起来与物理世界中发生的事情完全相同。 但是在所有其他情况下,情况并非如此。
 图 1个
图 1个晶格位移场
假设我们有一个由晶体组成的介质,该晶体的原子彼此之间等距均匀分布。 我把它们画在照片上。 一维2维-您可以想象具有3维维的类似情况,但是现在这将是不必要的复杂化。 我还用红色标记了第10个原子,以使您更容易跟踪它们的运动。 而且我还大大夸大了原子之间的距离-假设每两个红点之间有几百万个原子,而不是10个。
我们看一下位移场D(x,t),它告诉我们通常在平衡点x处的原子在t时刻已从晶格中的该点移动了多少。 这意味着,在动画从其开始的静态状态下,该场到处都是零,D(x,t)= 0,因为所有原子都处于其通常位置。 然后,在动画中,单个原子开始来回振荡,并且它们的运动大体上以波的形式传播,从左向右传播。 在图的顶部,晶格位移场D(x,t)的图形显示了该场在波通过过程中的行为。 请注意,图中的字段。 尽管字段的物理解释非常不同,但图1和2的行为类似。
 图 2
图 2磁场方向
什么是永磁体? 它由一组原子组成,每个原子充当具有微小磁场的微小磁体,并且它们全部对齐,以便它们共同产生大磁场。 磁铁如图2所示。 3,其中每个原子都指向上方。 在这种情况下,取向场Θ(x,t)告诉我们在时间t处的点x处的原子偏离垂直方向多远。 简而言之,Θ是每个原子的磁体和垂直方向之间的夹角。 图中的动画。 图3示出了磁体中的波,其中原子磁体的方向左右摆动。 在绿色磁铁上方显示了曲线Θ(x,t); 而且他看上去和以前的情况完全一样。

气压场
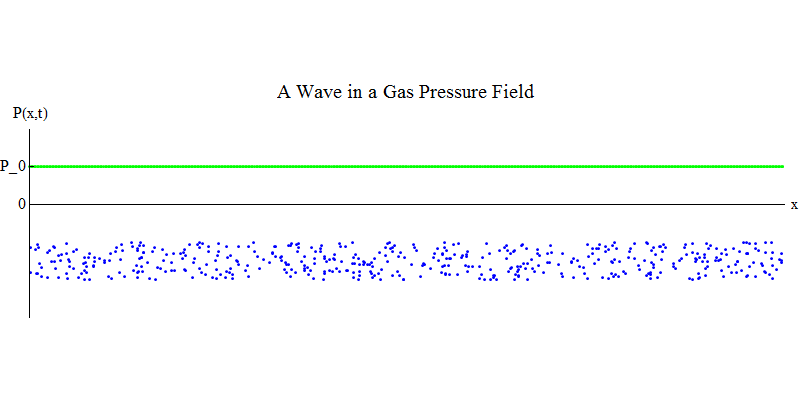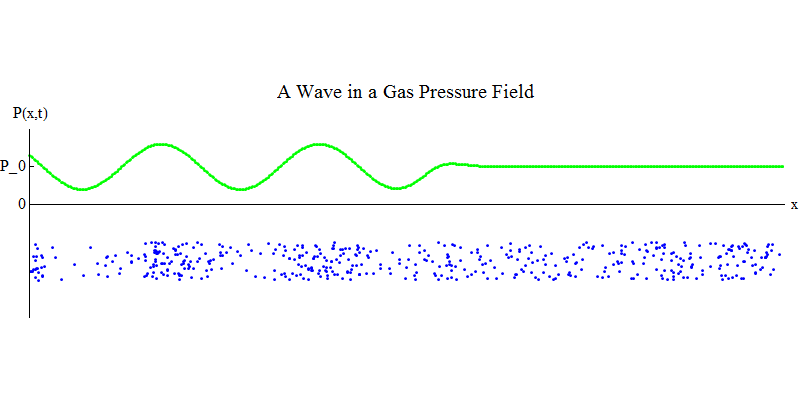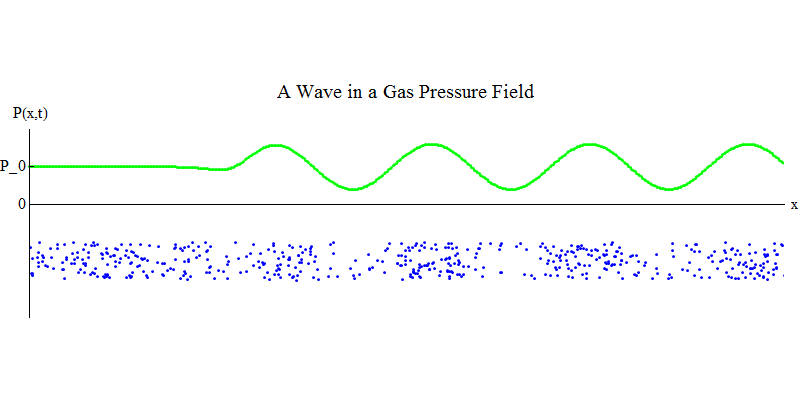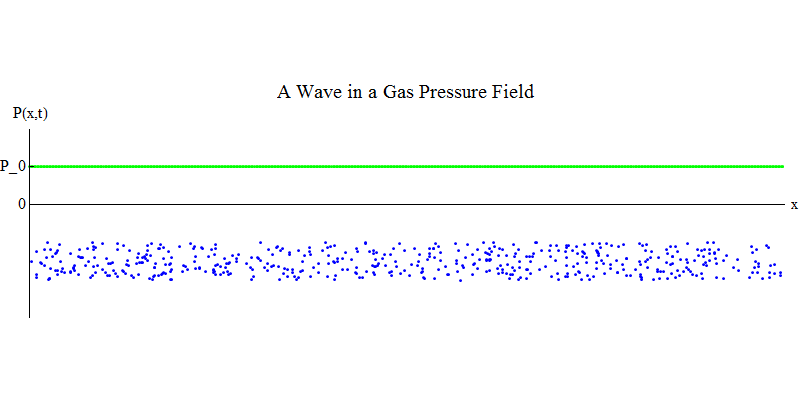
考虑长管中的分子气体。 沿管道的尺寸为x。 气体分子将几乎随机移动,与管道壁以及彼此碰撞。 在平衡状态下,密度(给定体积中的分子数量)和压力P(x,t)(作用在小球表面上的力在时间t出现在点x处)是恒定的。 但是,穿过气体的声波将导致压力和密度振荡,如图2所示。 4.密度和压力会定期增加和减少。 分子向前和向后移动,尽管平均而言它们根本不移动,但同时,波及其能量通过气体从左向右移动。 曲线图P(x,t)再次看起来与先前的曲线图非常相似。
重要课程
从显示0级波的四个示例中我们可以学到什么? (运动方程具有一个量cw,并且相应场中的所有波都以速度cw移动。0类的不同场将具有不同的cw值)。 我们可以发现,相同的字段行为可以从物理上不同的环境中存在的物理上不同的字段中出现。 尽管它们的起源不同,但从场的角度来看,高度场,晶格位移场,磁取向场和气压场中的波看起来是相同的。 它们满足相同类型的运动方程以及相同的频率和波长数值关系。
小字体:严格来说,如果您创建的波浪长度足够短,则仍然可以区分不同介质的行为。 只要波长等于绳子,晶体或磁体的原子之间的距离,波浪将满足的波动方程将比我们编写的方程更复杂,并且它们的详细信息将彼此区分介质。 但是通常在实际实验中,我们甚至无法观察到这种效果。
这样的结果是,与波相关的波及其量子的研究并不一定会告诉您什么是介质,或者是该场的物理解释-它代表了介质的哪些特性。 而且,即使您以某种方式知道这是某种类型的字段(例如,压力场),您通常仍然无法从其行为中看出它所代表的压力。 通过研究波浪,您所能了解的就是该场是属于0类还是属于1类,以及cw的值是多少? 或发现该字段属于另一个类。
在某些情况下,这是非常糟糕的。 该字段仅发送有关环境的部分信息。 有时这很方便。 与它描述的物理材料相比,该领域是一个更加抽象和通用的事物。
因此,该字段未定义环境,其行为通常不取决于环境的细节和属性。 因为出现了什么问题。
在没有任何介质支持的情况下,是否存在一个物理场-由量子组成的波在空间中移动并传递能量?
没有介质的领域?
没有歌手就听不到歌曲。 但是这首歌有某种独立的存在。 听起来是不同的,具体取决于谁唱歌,但是与此同时,歌曲中还包含一些固有的东西,某种抽象的品质,因此可以始终识别它。 这种抽象实体是歌曲的旋律。 我们可以讨论,学习,学习旋律,并通过音乐录音将其录制下来,甚至听不到歌手演奏的旋律。 我们中的许多人甚至可以将它哼在脑海中。 即使没有人在演唱歌曲,旋律仍然存在。
如果在我给出的所有示例以及我可以给出的所有示例中,并且您可以直观地理解这些字段,那么该字段将描述属性,那么在没有环境的情况下,字段如何存在? 但是这些字段以某种方式独立于它们的环境,因为尽管许多不同的字段描述了完全不同的环境的许多不同属性,但它们的行为相同。 因此,有可能从环境中提取字段。
实际上,这不仅是可能的,而且似乎是必要的。 至少,有必要没有介质,或者有一种不能由普通物质创造的环境,这与我们考虑的所有介质根本不同,因为它的作用方式(根据所有实验)不存在。
爱因斯坦从1905年起就提出的相对论特殊理论的几个基本要素之一是,对于光波-几十年来一直在电场和磁场(电磁波)中使用波,并以相同的速度在空旷的空间中移动-没有介质。 只有字段。
假设的介质称为“醚”。 爱因斯坦认为这样的事情不存在,并写下了一组不需要的方程。 我注意到,关于是否需要想象与普通物质有很大不同的奇怪环境的存在,仍然存在着争论(通常是哲学上而非物理上的争论)。 迄今为止,没有证据要求其可用性。
爱因斯坦相对论版本(与伽利略和牛顿版本相对)的关键要素如下:
•空间和时间不是您认为的那样。 不同的观察者相对于彼此均匀地移动,它们对物体的长度和事件之间的时间间隔的估计会有所不同(并且这些差异可以准确地测量)。
•存在通用速度限制s; 任何观察者相对于物体的速度进行测量的观察者都会发现,该速度小于或等于s。
•在这样的世界中,某些领域-“相对论领域”-可以在没有媒介的情况下存在,并且它们满足特殊的运动方程。 最简单的相对论场满足类别0或1的运动方程,运动方程中提到的波速cw取值为c。
简而言之,存在满足以下等式的0类相对论场
光和所有电磁波是最著名但并非唯一的示例-因此,“ c”通常被称为“光速”。 并且有1类的相对论领域满足方程
我们将在下一篇文章中看到它们的示例。 注意,相对性并不对μ施加限制(除了需要使μ2
为正)或对Z
0都没有限制。 对于相对论领域,存在更多复杂的方程,但是在简单物理过程的描述中,大多数方程简化为这两个方程之一。
相对论领域在物理上是真实的,在宇宙中具有物理意义,即:
•它们的波将能量和信息从一个地方传送到另一个地方。
•一个场中的波浪会影响另一个场,并改变不存在时发生的物理过程。
但是,与本文中给出的示例的领域不同,相对论领域没有描述任何普通物理介质的属性,该介质由类似于普通物质的物质组成,并且就实验而言,它们并不描述任何事物的属性。无论如何 就目前我们所知,这些领域也许是宇宙的基本要素之一。