1.
牛顿弹簧上的球2.
弹簧上的量子球3.
波浪，经典外观4.
波浪，经典的运动方程5.
量子波6.
领域7.
粒子是量子8.
粒子如何与场相互作用因此，最后，我们达到了目标：了解我们所谓的“粒子”实际上是电子，光子，夸克，胶子和中微子。 当然，所有这些都适用于现代科学。 值得记住的是，在科学中，不能保证不会进一步加深当前的理解。
上一篇文章描述了什么是场-在空间的任何一点和时间的任何时刻（空间和时间的函数）具有意义，满足运动方程并且在物理意义上具有意义的对象，因为它们能够将能量从一个地方转移到另一个地方并影响宇宙的物理过程。
我们了解到，我们知道的大多数领域都描述了介质的属性，例如绳索的高度或气体中的压力。 但是我们也了解到，在爱因斯坦相对论中，有一类特殊的领域，相对论领域不需要媒介。 或者至少如果他们有一个环境，这是非常不寻常的。 场方程式中的任何内容都不需要存在任何介质，并且不表示相对论场描述了该介质的什么性质。
因此，目前，我们将相对论场视为宇宙的基本物理对象，而不是未知介质的某些特性。 这种观点是否会得到物理学家的进一步支持-时间会证明一切。
我们考虑了两类相对论领域，现在我们将更详细地研究它们。 它们要么满足运动的0类方程，其中c
w = c（其中c是通用速度极限，通常称为“光速”）。
或1类运动方程式，其中cw = c
在上一篇文章中，表明μ是此类场中的最小波频率。 在本文中，我们用νmin表示它。
为什么通用限速通常被称为光速？ 方程为0类的波以速度c
w移动。 在空空间中移动的光（表示任何频率的电磁波的总称）满足0类的相对论方程，因此，光波（以及满足0类的相对论方程的任何相对论场的波）以速度c移动。
此外，在同一篇文章中，我们看到如果1类场的波具有振幅A，频率ν，波长λ和平衡态Z
0 ，则运动方程式要求频率和波长与μ= νmin通过公式出现在方程中
这是毕达哥拉斯公式-如果需要，可以用三角形表示，如图2所示。 1.任何波的最小频率为νmin，并且赋值ν=νmin（因此，由于λ→∞）对应于将三角形压缩为垂直线（下图1）。 通过将μ=νmin设为零，您也可以获得类0的相似关系。 然后您可以提取平方根，并得到
这是一个压缩为水平线的三角形（图1，右）。 在这种情况下，最小频率为零。 磁场可以任意缓慢地波动。
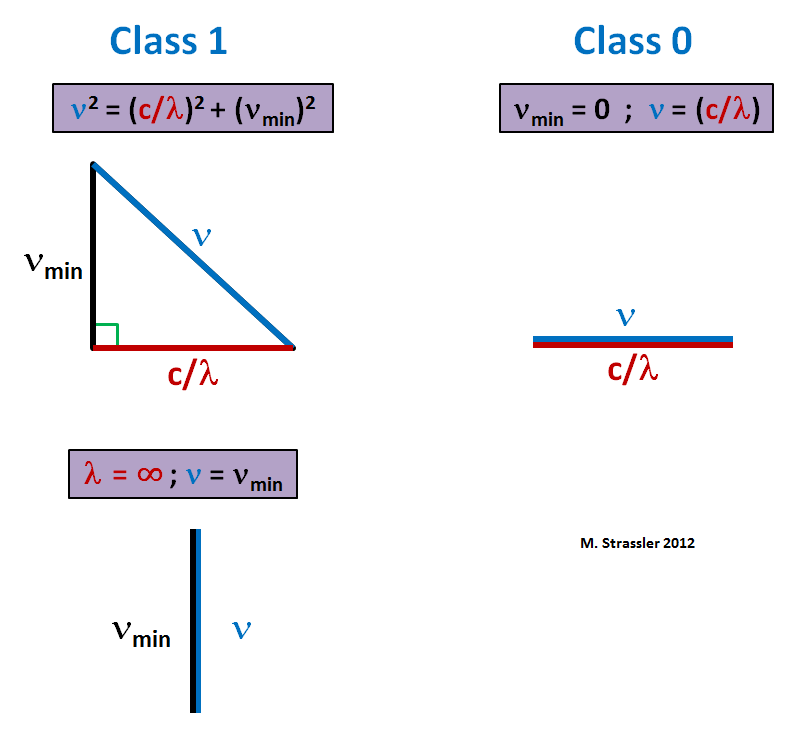图 1个对A没有限制。 但这是因为我们忽略了量子力学。 研究相对论量子场的时候到了。
相对论量子场
现实世界是量子力学的，因此振幅A不能为任何振幅。 它采用与n的平方根成比例的离散值，这是一个非负整数，表示波中的振动量子数。 波浪中储存的能量为
h是普朗克常数，必然出现在量子力学重要的地方。 换句话说，与每个振荡量子相关的能量仅取决于波的振荡频率，并且等于
爱因斯坦在1905年对光电效应的解释中首次提出了该比率，特别是针对光波。
但是，让我们回想一下我们的勾股比频率和波长。 如果将其乘以h
2 ，则得到1类量子场的值。
看起来很熟悉。 我们已经知道爱因斯坦相对论中的任何物体都必须满足描述其能量，动量和质量的方程式：
毕达哥拉斯的另一种关系。 物体的最小能量是mc
2 ，类似于关于1类νmin的波可以拥有的最小频率的陈述。 我们可能会想当然地认为，相对论领域的量子
第一个方程式最早出现在1924年的路易斯·德布罗意（Louis De Broglie）的作品中-距爱因斯坦近20年。 为什么要花这么长时间？ 我不知道
图 2这有意义吗？ 如前所述，0级相对论场也包括电场，它们的波是电磁波，即光。 我们为0类量子所获得的公式（*）的版本与1类字段的μ=νmin等于零（即m = 0）相同。我们提取平方根并获得
或无质量粒子的爱因斯坦方程。 电磁波的量子（包括所有类型的光：可见光，紫外线，红外线，无线电波，伽马射线等，仅在频率上有所不同，因此量子的能量）实际上将是无质量的粒子-只要应用所示以上两个方程（**）和（***）。 这些是光子。
从等式（***），我们最终可以计算出粒子的质量。 每个具有质量的粒子都是1类场的量子，这种波的最小频率为νmin。 这种波的一个量子的最小能量等于频率的h倍。 粒子的质量就是最小能量除以c
2 。
如果要了解粒子质量来自何处，则需要了解确定νmin的原因以及通常为何存在最小频率的原因。 对于诸如电子和夸克这样的粒子，这是完全不清楚的，但是众所周知，希格斯场在其中起着重要的作用。
我们得出的结论是：自然粒子是相对论量子场的量子。 无质量粒子是满足0级方程的场波的量子。具有质量的那些粒子对应于1级方程的场。有很多细节，但这是我们世界的基本基本特性之一。
这些量子真的表现得像粒子吗？
我们将颗粒想象为灰尘颗粒或沙粒。 从这个意义上说，量子不是粒子-它们是在特定频率下具有最小能量和振幅的波。 但是它们的行为非常像粒子，我们可以原谅在描述中使用“粒子”一词。 让我们看看为什么。
如果您在水中拾取波浪，然后让其穿过位于地面以下浅层的石头，则该波浪的一部分将穿过石头的线，而一部分将被反射，如图2所示。 3.波浪的哪一部分将穿过线取决于石头的形状，它们与表面的接近程度等。 但最重要的是，波的一部分通过石头传播，而一部分将被反射。 波能的一部分将以相同的方向传播，一部分将以相反的方向传播。
图 3但是，如果您向反射玻璃发送一个光子，则该光子将穿过它或被反射（图4）。 更准确地说，如果您测量光子的行为，则会发现光子是反射还是透射。 如果不进行测量，将不可能说出发生了什么。 欢迎来到量子力学的沼泽。 光子是量子。 它的能量不能分为穿过玻璃的部分和被反射的部分，因为这样一来，在每一侧上将存在少于一个的量子，这是被禁止的。 （小字体：玻璃不会改变光子频率，因此不能在两个或多个较低频率的量子之间分配能量）。 因此，尽管是波，但光子在这种情况下的行为类似于粒子。 它会从玻璃上反射或不反射。 不管它是否被反射，量子力学都无法预测这一点。 它仅给出反射的可能性。 但她预测，无论发生什么情况，光子都将作为一个单元传播并保持其身份。
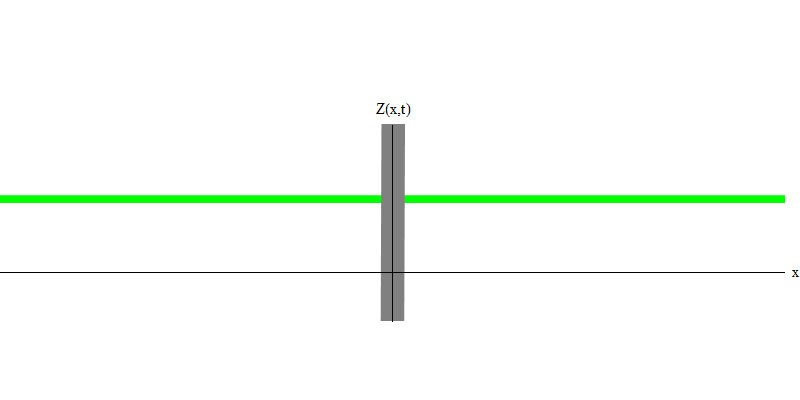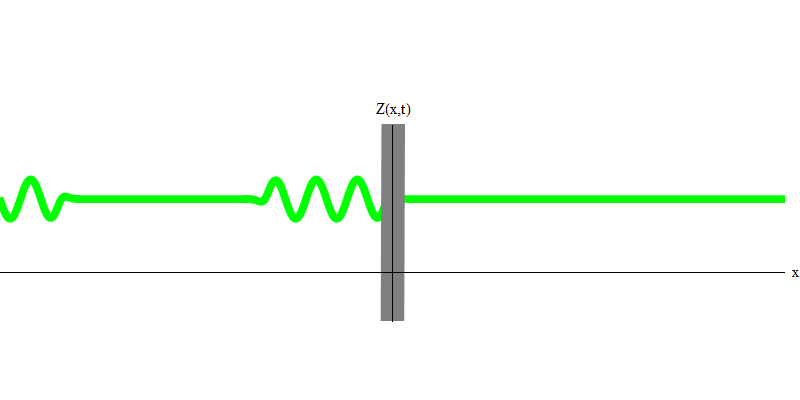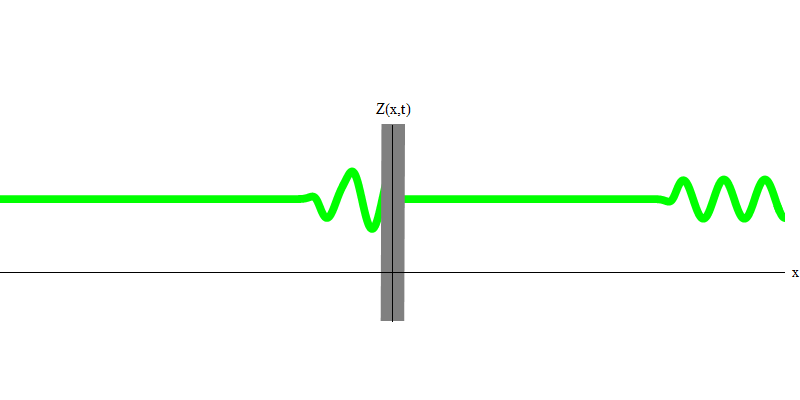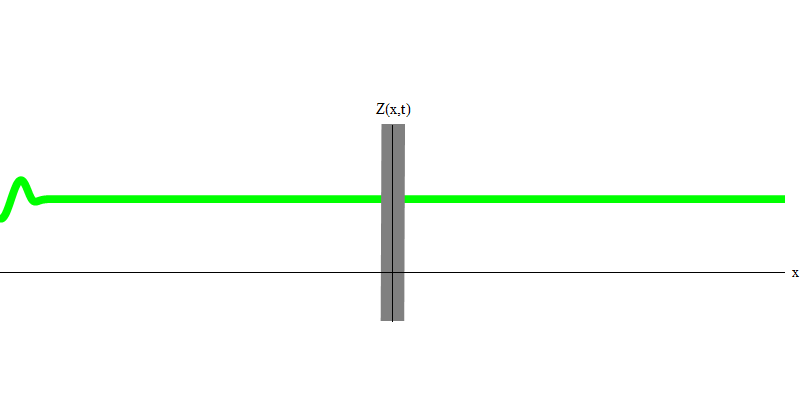图 4两个光子会发生什么？ 这要看情况。 例如，如果光子在不同的时间从不同的位置发出，那么观察者将看到两个量子，它们在空间上是分开的，并且可能朝不同的方向移动（图5）。 它们可以具有不同的频率。
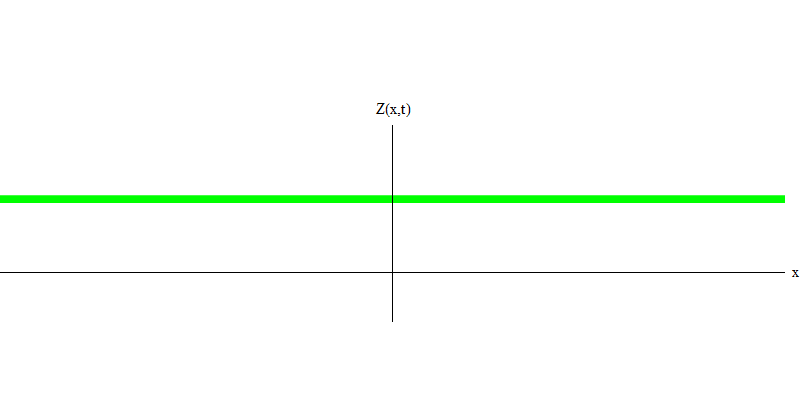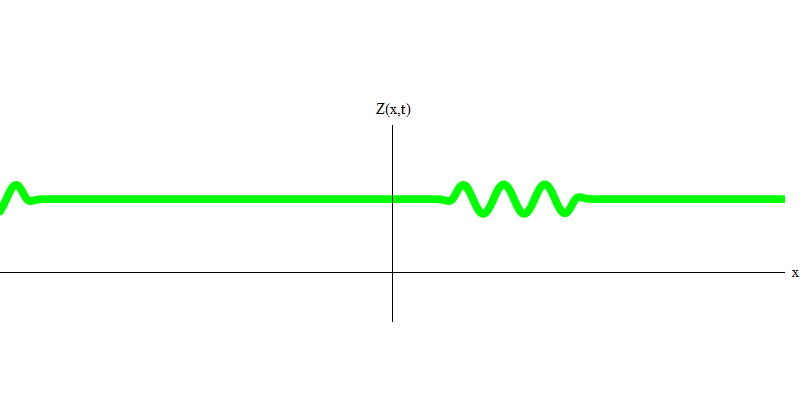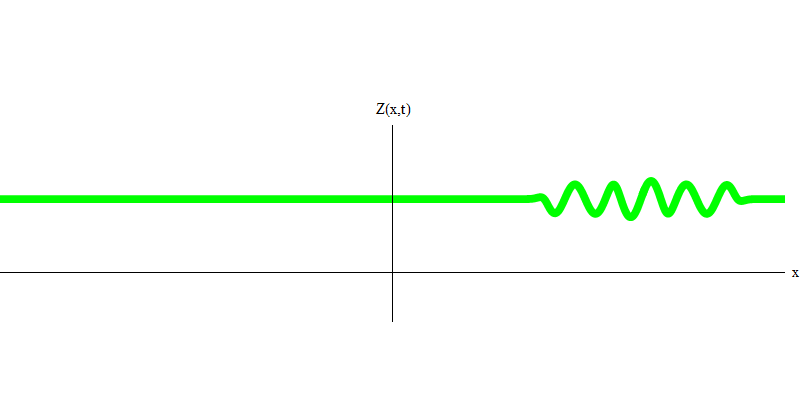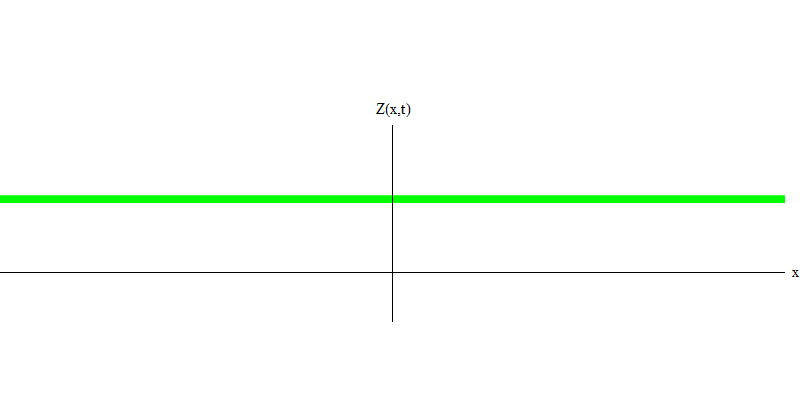图 5：独立量子在特殊情况下，当两个光子同时且完美地同步发射时（如在激光中），它们的行为如图1所示。 6.如果我们将两个光子的组合发送到玻璃上，则不会发生两个，而是会发生三件事。 两个光子都将穿过玻璃，或者两者都将被反射，或者一个将通过，而另一个将被反射。 玻璃将反射0、1或2个光子-没有其他选择。 从这个意义上讲，光量子又像粒子一样表现为小球，如果您将两个球扔进有孔的网格中，则0、1或2个球将从网格中反射出来，而0、1或2个球将穿过这些孔。 不可能从网络中反映出1,538个目标。
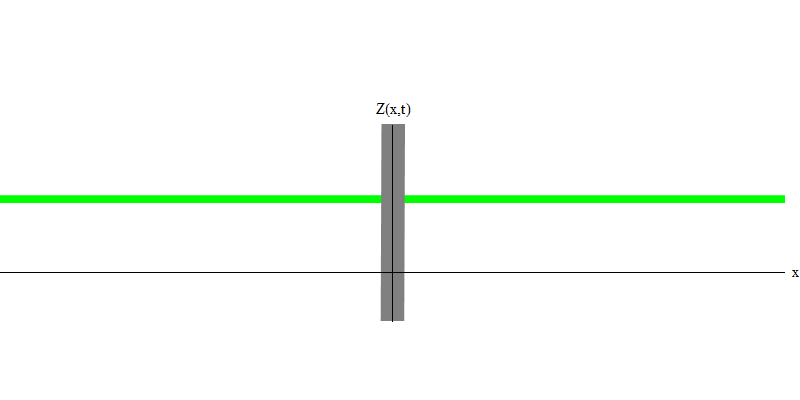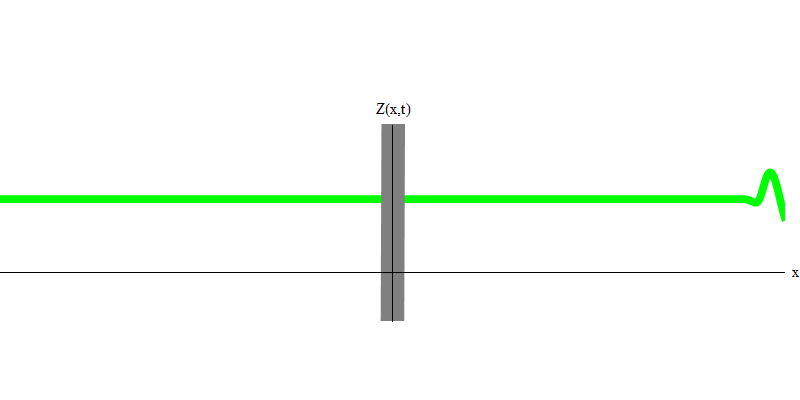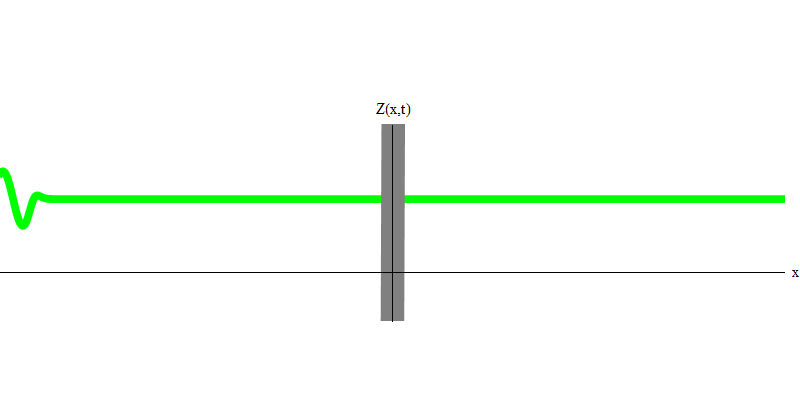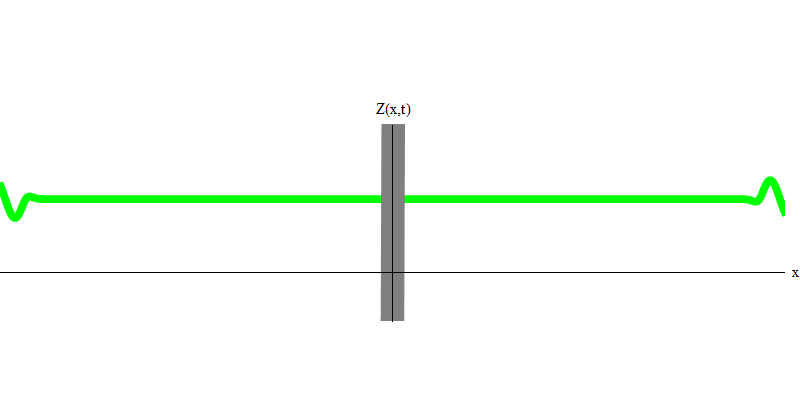图 6但是这些是无质量的光子，必须以光速和E = p c移动。 质量像电子的粒子呢？ 电子是电场的量子，像光子一样，它们可以整体被发射，吸收，反射或传输。 他们有一定的精力和动力，
其中，m
e是电子的质量。 电子和光子之间的区别在于它们的运动比光慢，因此可以静止。 静止电子的这种事件的草图（在量子力学中，由于不确定性原理，没有什么可以是真正的静态）。 7.这是通过分配非常大的几乎无限值的波长获得的最小频率的波。 因此，图1中的空间波形为 没有显示任何卷积-它只是随时间波动。
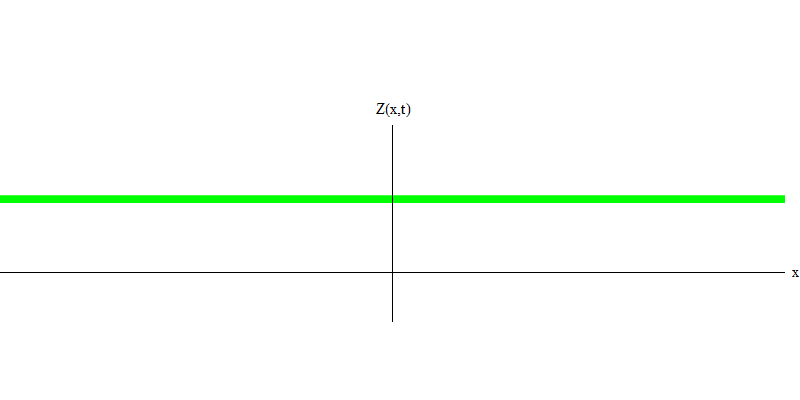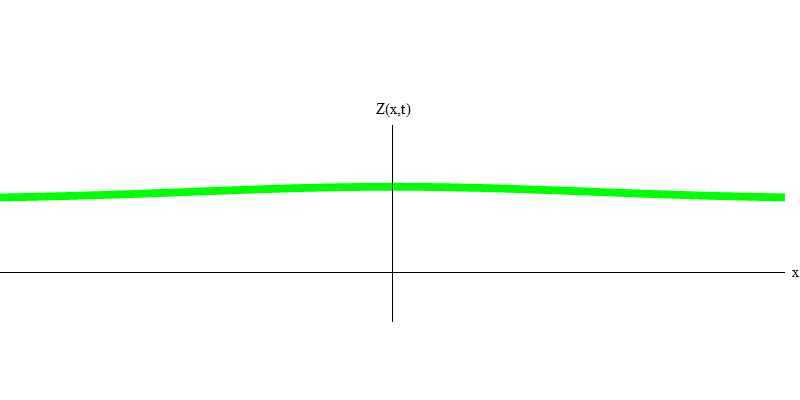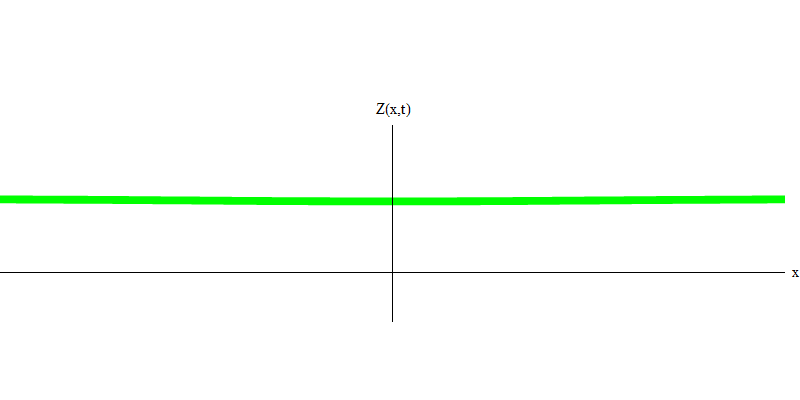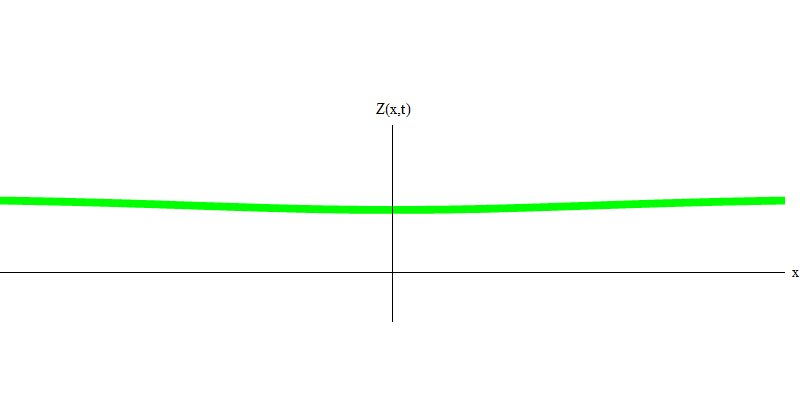图 7因此，是的，事实上，量子的行为非常类似于粒子，因此将电子，夸克，中微子，光子，胶子，W粒子和希格斯粒子称为“粒子”将不会是灾难性的欺骗。 但是“量子”一词更适合于此-因为这些恰恰是量子。
费米子和玻色子有何不同？
•所有基本粒子都分为费米子和玻色子。
•费米子（包括电子，夸克和中微子）满足
保利排斥原理 -两个相同类型的费米子不能做相同的事情。
•玻色子（包括光子，W和Z粒子，胶子，引力子和希格斯粒子）是不同的：两个或更多个相同类型的玻色子可以做相同的事情。
这就是为什么激光可以由光子组成的原因-因为它们是玻色子，所以它们可以处于同一状态并产生强大的一束光线。 但是激光不能由费米子的电子构成。
这种差异如何在数学语言中体现出来？ 事实证明，我带来的公式适用于玻色子，而对于费米子，则需要对其进行更改-稍作改动，但后果不堪设想。 对于玻色子，我们将有：
这意味着每个量子的能量等于hν。 这意味着玻色子量子可以做同样的事情。 当n大于1时，波场中的波将由几个量子共同振荡并运动。 但是对于费米子：
一个量子的能量仍然等于hν，因此关于粒子及其能量，动量和质量的整个讨论仍然有效。 但是，电子波中的量子数量只能是0或1。与十个光子不同，十个电子不能组织成一个振幅更大的波。 因此，没有由大量的费米子组成的费米子波一起振动和运动。