我们了解粒子物理学：8）粒子如何与场相互作用

了解粒子物理学：
1. 牛顿弹簧上的球
2. 弹簧上的量子球
3. 波浪，经典外观
4. 波浪，经典的运动方程
5. 量子波
6. 领域
7. 粒子是量子
8. 粒子如何与场相互作用

希格斯场如何工作：
1. 主要思想

在系列的上一篇文章中 ，我解释了自然粒子是相对论场的量子，它们满足0类和1类的运动方程。但是到目前为止我还没有说过，所以幸运的是，这种说法只是部分正确。 实方程总是有点复杂，因此仍然存在粒子和场的互连，但是可能出现更多种不同的现象和过程，包括其他粒子碰撞后出现的粒子，粒子分解为其他粒子以及粒子彼此散射。以及质子和中子，原子核和原子之类有趣物体的形成。 我将无法详细解释所有这些内容，但是在本文中，我将向您介绍这一切的工作原理。

这些方程式（我称之为“ 0类”和“ 1类”）与对实际物理具有重要意义的方程式之间的主要区别在于，在实际方程式中，还有一些附加项依赖于两个或多个领域，而不仅仅是一个。 就是说，相对论字段Z（x，t）代替了类0的方程，它看起来像

$$

$$d ^ 2Z / dt ^ 2-c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

对于实场，方程看起来更像这样：

$$

$$d ^ 2Z / dt ^ 2-c ^ 2 d ^ 2Z / dx ^ 2 = y'Z（x，t）^ 3 + y A（x，t）B（x，t）$$

其中y和y'是数字（通常小于1），Z是Z（x，t）的缩写，A（x，t）和B（x，t）是一对其他字段。 在这样的方程式中，可以预期出现以下项：A（x，t）Z（x，t）或A（x，t） ² Z（x，t）或Z（x，t） ²甚至A （x，t）d ² Z / dt ²等 哪些成员可以出现，哪些成员不能出现，取决于过程中涉及的字段的详细信息。 这些规则很严格，但是很混乱，因此我们暂时不讨论它们。 通常，通过实验，我们确定（并从理论角度理解）本质上：

•原则上有效的任何术语（电荷守恒或爱因斯坦相对论的对应）都出现在方程式中，
•但是具有多个字段的成员与具有一个，两个，有时三个字段的成员相比通常很小且微不足道（具有时间或空间导数的成员通常也很小）。

因此，在最有趣的物理过程中，人们可以专注于具有一个，两个或三个字段的所有有效术语。

一点术语。 具有场的方程式中的项在第一级称为线性。 0类或1类方程式中的所有项都是线性的。 具有两个或三个字段的成员称为二次方或三次方。 通常，它们称为非线性。 我们世界上所有有趣的现象都是由于运动方程中的非线性项而出现的，即场之间以及彼此之间的相互作用。 让我们研究其中之一。

其他两个人的共鸣产生了新的浪潮

为了了解一切将变得多么有趣，我们采用三个字段A（x，t），B（x，t），C（x，t）和简化情况。 假设场A和B近似满足0级方程（并且包含无质量的量子），并且场C满足1级方程（包含具有最小频率νmin的波，因此满足质量m = hνmin / c ^2的量子，其中h -普朗克常数）。 我们还将非线性项添加到它们的方程式中。 具体来说，像这样（为简便起见，我们将用“ A”代替“ A（x，t）”，以此类推，c是光速，y是通常小于1的数字）：

$$

$$d ^ 2A / dt ^ 2-c ^ 2 d ^ 2A / dx ^ 2 = y BC \\ d ^ 2B / dt ^ 2-c ^ 2 d ^ 2B / dx ^ 2 = y AC \\ d ^ 2C / dt ^ 2-c ^ 2 d ^ 2C / dx ^ 2 =（2 \ pi \ nu_ {min}）^ 2 C + y AB$$

精美的文字：我在所有三个方程式中都添加了非线性项，因为一个方程式中存在此类项而另一个方程式中不存在此类项会导致矛盾。 例如，能量将不会被保存。 对于我正在描述的过程，我们将只需要考虑磁场C的运动方程中的非线性项。

让我们看看如果场A的波与场B的波相遇时，这组方程会发生什么。原则上，我们可以通过应用仔细检查的方法来猜测。 如果在A场中有波，则A（x，t）在它附近不为零。 当场A和场B的波彼此重叠时，将A（x，t）和B（x，t）相乘的结果变为非零。 现在我们来看C的等式：时空C场中的变化（左侧的两个项）与乘积A和B（右侧的一项）相关。

$$

$$d ^ 2C / dt ^ 2-c ^ 2 d ^ 2C / dx ^ 2 =（2 \ pi \ nu_ {min}）^ 2 C + y A B$$

因此，即使当A（x，t）B（x，t）变为非零时字段C为零，那么C（x，t）在同一部分中也将很快变为非零。 简而言之，由于波A和波B的相遇，将对场C产生某些小的干扰。

小字体：您可能感兴趣-在C变为非零之后，是否将A（x，t）C（x，t）项包括在磁场的运动方程中，这会引起磁场B的其他干扰。答案是肯定的，但是这种效果会甚至更小。 直到我们忽略他，然后再找出为什么值得这样做。

在图。 图1显示了在场A（绿色）中频率为ν的波，在场B（蓝色）中频率为ν的波。 为了简单和对称，我均衡了频率。 稍后我们将了解为什么其他情况可以归结为这一点。 速度ν可以通过观察绿波和位于空间中某一点的垂直线并与波一起振荡来估算。

下面的橙色乘积显示乘积A（x，t）B（x，t）； 可以看出，当两个波叠加时，它变为非零。 还可以看到它随时间变化。 您可以看到（与垂直摆动条进行比较），A（x，t）B（x，t）振动的速度是原来的两倍。 记住这一重要事实。 通常，如果频率波ν1与频率波ν2相遇，则它们的乘积将以频率ν1 +ν2振荡。 还有一件事：您会注意到AB振动不会左右移动，而是保持在原位。 稍后我们将了解为什么这很重要。


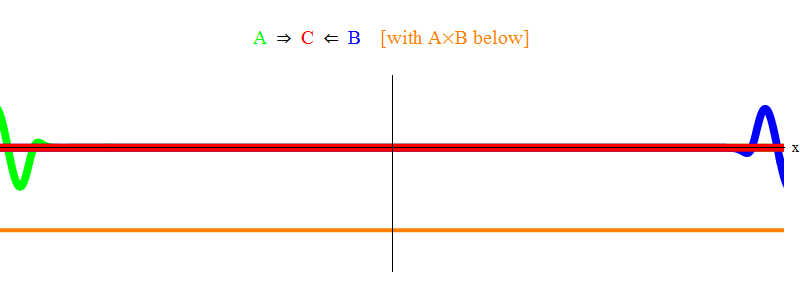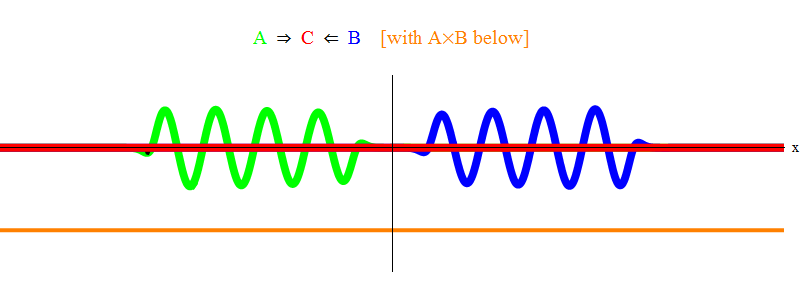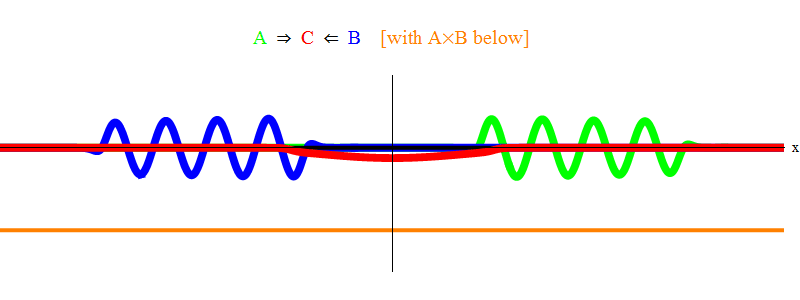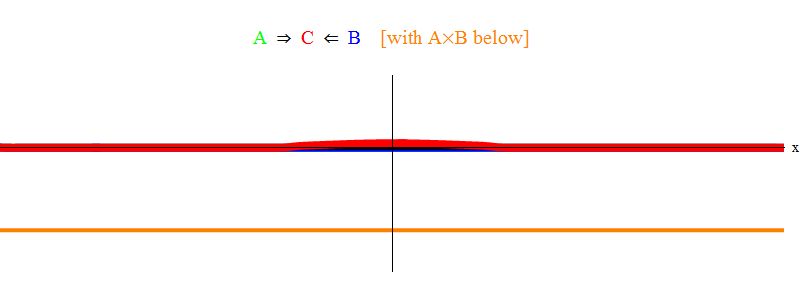图 1个

AB的非零值如何影响C？ 答案高度依赖于频率ν。 首先，我将为您提供一个现成的答案，然后对原因进行大概的解释。 实际上，这是共鸣 。 共振是包括波在内的所有振动（振动）的整体现象。 我已经描述了弹簧上的球如何以固有频率振荡，以及如果力的振荡频率与弹簧上的球的固有频率一致，推动球的振动力将如何引起共振。

了解了共振之后，您将看到以最小频率和零水平速度振荡的磁场C表现得像弹簧上的球，而AB表现出试图使球振荡的振荡力。 因此，如果振动频率AB-2ν-是磁场C-νmin的最小频率，则会发生共振现象。 更具体地说：

•如果2ν不等于νmin-如果力不共振-则在AB不等于0的区域中，C将开始以小幅度不规则地波动。
•如果2ν=νmin-如果力处于共振状态-那么C将在AB不等于0的区域内以大幅度平滑地振荡，并且即使AB再次变为零也将继续波动。

图 图1仅示出了共振情况2ν=νmin。 可以看出，当波A通过波B时，它们离开固定波C，以频率νmin振荡。 精美印刷：如图。 显示的是草图，而不是方程式的精确解。 确切的解决方案将具有许多小的复杂功能，这些功能掩盖了基本的物理含义，因此为了清楚起见，我将其删除。 稍后，我们将考虑一种没有共振的情况，这种情况要复杂得多，但对物理也更重要。

其他两个的an灭产生了一个新的粒子

我刚刚向您演示了，如果场A和B的频率之和等于场C的最小频率，则方程C中的非线性项AB会引起波A和B的叠加产生场C的振荡。但是如果这些波具有幅度很小？ 如果一个场A的量子遇到一个场B的量子怎么办？

•如果频率AB进入与场C的共振，则可能会出现场C的量子，即实粒子C，而量子A和B将消失-“ an灭”。
•同样，量子A和B可以简单地彼此传递，而不会产生粒子C。
•量子力学定律表明，创建粒子C的概率与y的平方成正比，然后乘以运动方程C中的AB。
•如果频率未进入共振，则不会出现真实粒子C。 但是，在场C中可能会出现临时干扰，这是通常称为“虚拟粒子” C的示例，在这种情况下，量子A和B可能会消失。 这种干扰的结果是什么？ 我在文章的“尾部”部分中部分描述了此过程。

这是事物的一般状态。 让我们深入研究细节。

对于粒子（即场A，B和C的量子）意味着处于共振状态还是非共振状态意味着什么？ 值得记住的是，由于方程E = hν，量子的能量与频率有关。 因此，我们将对波的讨论转换为对粒子的讨论。

假设我们在场A和B中的波由一个量子组成。 这些量子是无质量的，因为A和B满足类别0的方程。更精确地，它们的运动方程中的线性项与类别0的方程相同。由于量子A和B具有相同的频率，因此它们具有相同的能量E = hν。 由于无质量量子的动量为p = E / c，因此量子A和B的矩量级等于hν/ c，但方向相反，因为它们中的一个向左移动，另一个向右移动。 因此：

•两个量子的总能量将为2hν。
•两个量子的总动量将为零。

由于能量和动量是守恒的，两个量子碰撞后的总能量将保持等于2hν，总力矩将保持为零。

在波浪的情况下，我们看到由于C的方程包含形式AB的项，因此当频率AB（作为振荡力）与最小频率C（如弹簧上的球一样）重合时会产生共振。 我们将此陈述转换为量子。

频率AB将为2ν，因此，当波A和B由一个量子组成时，乘积A和B的能量等于能量A和B的总和。

$$

$$E_ {AB} = 2小时\ nu = E_A + E_B$$

最小频率C等于νmin，这意味着对于固定的场C量子，动量为0，能量为

$$

$$E_C = h \ nu_ {min} = mc ^ 2$$

其中m是量子C的质量。

对于共振，需要2ν=νmin，即：

$$

$$E_A + E_B = 2 h \ nu = h \ nu_ {min} = mc ^ 2 = E_C$$

简而言之，当粒子A和B的相等能量之和（在我们的情况下，脉冲的大小相同而方向相反）恰好足以生成固定粒子C！时，就会发生共振。 在此过程中，粒子A和B被an灭-它们的能量完全进入生成粒子C的状态。 2，您需要与无花果进行比较。 1。


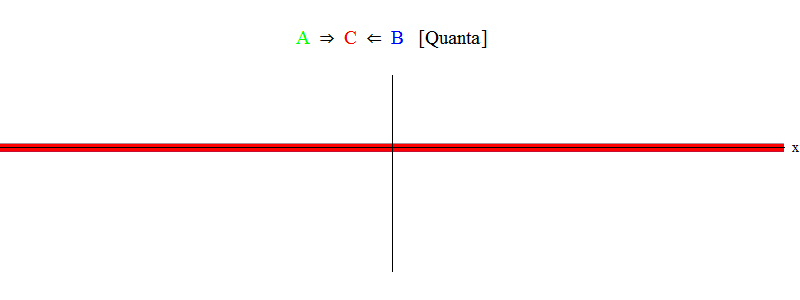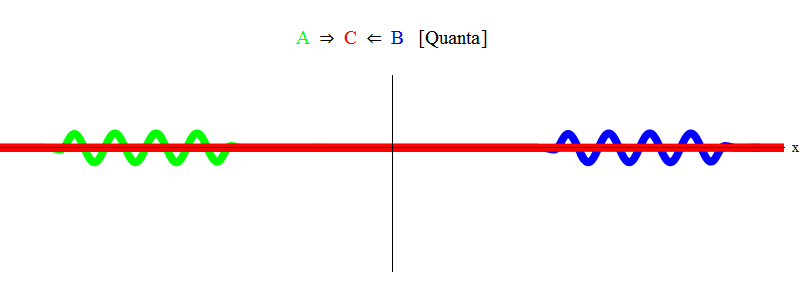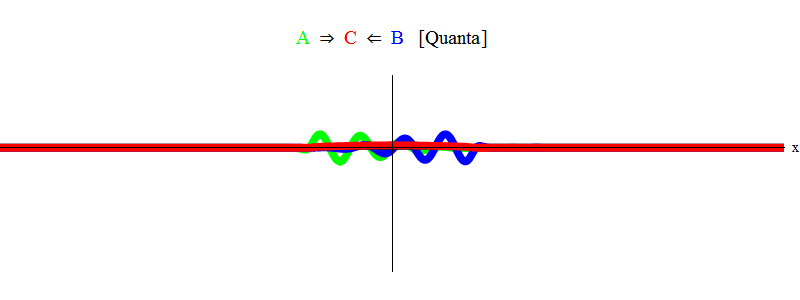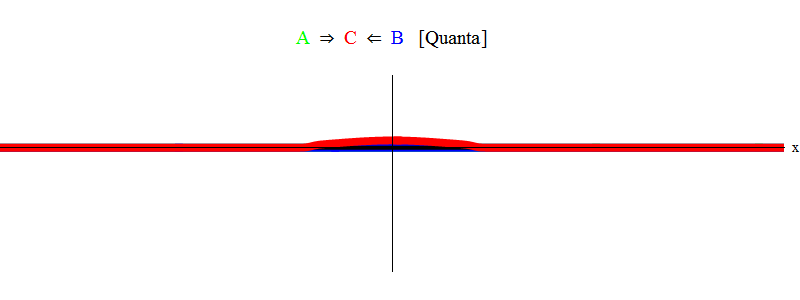图 2

推论

我只是向您展示了过程A + B→C。在我的解释中，我使用了三种不同类型的粒子来避免混淆。 但是相同的想法允许人们经历A + A→C形式的过程（例如，胶子+ gluon→希格斯粒子，基本上这就是在大型强子对撞机中获得希格斯粒子的方式）和形式A + A *→C的过程，其中A * -A的反粒子（例如，夸克+反夸克→Z粒子，这就是通常在LHC上获得Z粒子的方式）。 只需更改次要细节，但本质保持不变。

代表相同想法的另一个过程，只是在时间上相反-粒子的衰变。 希格斯粒子衰减为两个光子，或Z粒子衰减为夸克和反夸克，如图1中的动画所示。 2，朝相反的方向前进。

尾巴

1.如果项AB扰动场C而没有共振-如果2ν≠νmin-会发生什么？ 您可能还记得，如果您以错误的频率与孩子一起挥杆，或者对弹簧上的球施加力，并且其振荡频率与振动的固有频率不一致，那么您会得到振幅不均的不均匀振动。 在当前情况下，场C也会发生同样的事情。场C会以某种方式表现出来，但这不会导致表现良好的量子C的出现。这只是有些担心。 这种恶劣的愤慨是所谓的一个例子 “虚拟粒子C”-但这不是粒子（场C的量子），尽管其名称如此。 它的质量不同于粒子C的质量。 它可以更大或更小。 与粒子C不同，它长时间不存在。 并且它不满足实际量子必须满足的振幅条件。 相反，与图C中存在一段时间的粒子C不同。 如图2所示，仅当A与B相交时才存在非共振扰动。

但这并不意味着它不影响任何东西。 例如，它可能导致粒子A和B彼此反弹。

$$

$$A_ \ rightarrow + B_ \ leftarrow→C_ {暴怒}→A_ \ leftarrow + B_ \ rightarrow$$

通常，在三维空间中，回弹或散射会导致A在任何方向上移动而B在相反方向上移动的事实。 这种过程的示例包括由于虚拟光子引起的电子和正电子散射，或由于虚拟胶子引起的夸克和反夸克散射。

在D和E存在其他场的情况下，它们与C相互作用并参与运动方程C

$$

$$d ^ 2C / dt ^ 2-c ^ 2 d ^ 2C / dx ^ 2 =（2 \ pi \ nu_ {min}）^ 2 C + y A B + y D E$$

可能会发生更多有趣的过程：

A + B→C _扰动 →D + E

是的：由于虚拟粒子C，粒子A和B可以消灭，并导致出现新粒子D和E。这是创建新粒子的第二种方法！ 例如，电子可以与正电子发生碰撞，通过虚拟光子（灭（请记住，这意味着“通过以与共振不符的频率对光子场进行扰动”），然后变成μ子和反μ子，或夸克和反夸克。 下夸克和上反夸克可以碰撞，通过虚拟的W粒子歼灭，并变成电子和反中微子。 或两个胶子可以碰撞，通过虚拟胶子歼灭，然后变成上夸克和上反夸克（这是在LHC上获得上夸克的最常见方法）。

2.如果场A和B中的两个波具有不同的频率νA和νB怎么办？ 在合适的频率下，粒子C可能仍会出现，但是共振条件将有所不同，并且生成的粒子C将不会静止。 让我们弄清楚。

如果它们具有不同的频率，那么两个碰撞的无质量量子将具有

•各种能量 $$$E_A = h \ nu_A$ 和 $$$E_B = h \ nu_B$
•各种冲动 $$$p_A = + h \ nu_A / c$ 和 $$$p_B =-h \ nu_B / c$ （在这里，加号表示右边，负号表示左边）。

现在总动量p _A + p _B不为零。 但是这种势头依然存在。 因此，如果粒子C由于粒子A和B的an灭而发生，它将具有动量p _C = p _A + p _B ，因此它将向左或向右移动，并且不会停滞。 如果νA>νB，它将向右移动，否则向左移动。

产生运动的粒子C需要多少能量？ 为此，比静止的能量需要更多的能量-像任何大颗粒一样，其能量和动量必须满足

$$

$$E_C ^ 2 =（p_Cc）^ 2 +（mc ^ 2）^ 2$$

这意味着如果p _C = 0，则E _C = mc ^2；如果动量不为零，则E _C = mc ² 。 能量和动量守恒定律告诉我们：

$$

$$E_C = E_A + E_B$$

$$

$$p_C = p_A + p_B = E_A / c-E_B / c$$

我从哪里得到最后一个方程式？ 对于无质量的粒子，p = E / c，对于碰撞的粒子A和B，它们的动量是相反的，因此它们的符号不同。 将其替换为前面的公式即可得到：

$$

$$（E_A + E_B）^ 2 =（E_A-E_B）^ 2 +（mc ^ 2）^ 2$$

术语E _A ²和E _B ²相互抵消，并且将术语E _A E _B移到左侧，我们得到：

$$

$$4 E_A E_B =（mc ^ 2）^ 2$$

除以h ²并使用关系m =hνmin / c ² ，我们得到共振条件：

$$

$$（2 \ nu A）（2 \ nu B）= \ nu_ {min} ^ 2$$

当νA =νB到静止粒子C的等式2ν=νmin时，它正确地减小。 如果不满足此条件，则无法创建粒子C。 如果满意，那就有可能。

3.我注意到，与磁场C的运动方程包含项AB相同，因此磁场B的方程包含项AC。 回忆这些方程式：

$$

$$d ^ 2B / dt ^ 2-c ^ 2 d ^ 2B / dx ^ 2 = y A C$$

$$

$$d ^ 2C / dt ^ 2-c ^ 2 d ^ 2C / dx ^ 2 =（2 \ pi \ nu_ {min}）^ 2 C + y A B$$

因此，如果波A和B的叠加导致在场C中出现波，则使其变为非零值，如图2所示。 1，我们是否需要担心这个新波C与现有波A重叠并导致场B发生变化的事实？ 我回答说：“是的，但是我们可以忽略这一点。” 由于两个原因的结合，我们可以忽略。

首先，由于数字“ y”出现在AB和BC的乘法运算之前。 对成员AB的场C的影响与y乘以B的乘积成正比。对成员AC的场B的影响也与y乘以C的乘积y乘以y，但这又等于对y ²乘以A的乘积y。乘以A乘以B。只要y小于1，y ²就会小于y，因此，与AB成员对C的影响相比，AC成员对B的影响很小-至少对于小浪A和B而言。在实践中，这些波通常很小：粒子A是场A中波的一个量子；因此，波A的振幅很小 d。

从中可以得出第二个更奇怪但更令人信服的理由：我们看到，如果一个量子A遇到一个量子B并变成一个量子C，则波A和B消失（ni灭）。创建C之后，不再存在任何波A，因此AC为零，即对场B无效。

最后一点：尽管没有其他计算也无法证明这一点，但是即使A波和B波由一个量子组成，如图2所示。2，则过程如图。如果y大于1，则2会复杂得多。因此，我讲的故事简单起见，要求y的值较小。实际上，粒子物理学中的大多数非线性项通常很小，因此我所说的适用于大多数实际适用的情况。异常非常有趣-它们导致了质子和其他强子等复杂物体的产生。