最初的公理 ：如果我们假设物质的产生，其日趋复杂的多样性的后续转变和表现离不开运动，那么认知的主要且显然是唯一的问题是澄清物质主要属性的起源-实际运动。 在这种情况下，仍然可以假设仅存在一个拓扑环境，该拓扑环境由无限和有限两个结构部分组成。 这些对立面彼此定义，没有另一对面就不存在。 因此，有限和无限的相互作用是物质的体现。
物质表现的物理学。 首先，我们注意到任何封闭的壳体都会将拓扑环境分为两个部分（区域）：内部和外部，或者有限和无限。 此外，如果封闭的壳体与内部区域的中心均匀地间隔开，则不可避免地采取球形。 该壳的收缩运动意味着内部区域趋向于小而最终的状态，而外部区域趋于于向大而无限的方向发展。 同时拉伸外壳会导致共轭反作用。 下极性下限的存在（它不能为零，因为物质的定义会丢失，所以不能为零）分别对大状态的表达施加了限制。
因此，物质的表现范围受到中，大，小状态共轭抽吸的限制，并且与球形壳的收缩和伸展有关。 但是，小和大的比率和增长率却大不相同。 例如，如果将外壳尺寸减半，则内部区域的体积减少八倍，而我们强调的是，相应地，外部区域的体积同时增加将是微不足道的。 换句话说，拓扑环境向小规模的趋势显着地表现出来，而对大环境的相应渴望却是微不足道的。 但是两极是等价的，这意味着对环境的这些渴望也必须以同样的方式体现出来！ 也许这就是拓扑环境中最严重的张力的表现，需要保持平衡！
同样重要的是要注意，在边界壳体的离心抽吸中，球形表面的面积呈三次方递增，并且径向运动（脉冲）的强度可能会降低。 因此，在离心过程中在连续的同心夹层之间观察到的稀疏过程和在向心过渡过程中的脉冲凝结已经与两个相互垂直方向上的横向（横向）脉冲联系在一起，从而产生并增强了圆周运动。 换句话说，同心品种（旋转运动）的增长可以补偿径向运动的减弱。 反之亦然。 这些在三个垂直方向上相互关联的变化一起生成广义单位，生成一致的运动量。
实际上，正是由于这两种运动的反复交替和协调，才实现了与相应的径向同心层相互内置的一组球形壳体的实现，以及它们从最小到最大的顺序过渡，反之亦然。 边界区域由宏观的多层拓扑空心球表现出来，该空心空心球由许多相互缠绕的同心层组成。
然后，边界区域的总应力均匀地分布在给定的彼此内置的一组壳内，最初定义了一种由玩偶建造的相互布置形式。 因此，可以将有关物质知识的整个后续问题简化为研究所呈现边界层表现形式的特征。 它是特定的，并且包含物质的深层遗传本质。 因此，引入一个新概念是合乎逻辑的：例如，胚胎状态或仅是宇宙的胚胎（图1）。 为了使认知的棘手和蜿蜒的道路变亮，这种多层嵌入（嵌套）的设计可以平滑地改变关系和拓扑极性的过渡，可以用漫画图来说明（图2）。
图 1.以一般形式以及在运动流的情况下边界区域的初始状态的肖像（r是曲率最大为C max的最小球形中间层的半径； R是曲率最小为C min的最大中间层的半径）因此，小努力成为大。 到达无限大后，它的运动方向改变为相反方向，依此类推。 广告无限。 前述可以表示为宏观多层拓扑球的脉动，并将其与弹性下降并相应旋转的球从某个表面周期性地掉落和回弹相关联。 因此，您可以想象一下电压继电器（惯性）从最大浓度到最小中心气泡（反之亦然）的传输的物理图景，再加上径向运动相互转换成圆形（反之亦然）的过程，总之一定。 结论：运动的惯性是物质表现的本质，它从一开始就伴随着它。
图 2.开玩笑的形象是“嵌套娃娃”结构的物质结构
必须承认，大量带有薄中间层的球形壳的内置形式（径向同心运动形式）是非常密集的物质堆积。 通过壳的内部凝结，很容易实现一个无限小的地方（字面上的边界为零），但是，大环境在环境中的共轭表现（相信它们是等效的）仍然非常适度。
注意到物质的简洁表现，显然可以给出更具体的拓扑基础。 因此，在胚胎中，所有径向运动，包括发散和会聚的波纹，都得到了最充分的呈现，无一例外。 然而，从中央微泡向外周膜反之亦然，有条件地沿顺时针和逆时针方向运动的同心变化却从宏观的角度被这种极端的膜所限制。 另一方面，如果未找到并建立该极限，则离心方向上的同心脉动本身（反之亦然）及其相互转换将是有问题的。 但是相互嵌入的球形壳压缩状态的主要缺点（局限性）是它们都是单侧弯曲的-向内弯曲，仅实现一个中心，并且不被曲率相反，具有相应中心的壳平衡。
从集成的，闭合的，一侧弯曲的形状切换为极性比率的平行（并排，打开，全面展开）拓扑时，无限大介质的表现形式的其他储备会稍微打开。 在这种情况下，通过重复地分成两半（平衡，因此在每次动作过程中都沿着外壳溶解），通过几何级数将胚按体积方向由内向外翻转，直到球完全分层为最小的外壳。 在这方面，宇宙的体积增加了很多倍，没有任何通货膨胀和大爆炸。
宇宙胚胎拆包力学显然，在上外层中，径向和同心脉冲是相等的，因此，在离心向心运动方向上发生的定向丢失了。 但是有可能在相反的方向上使胚的外球形表面的区域局部弯曲。 换句话说，由于在这组层中发生共振现象，自然会出现“凹痕”。 当一对凹痕出现在胚胎的直径相对的区域中时，它通过径向相对的轴转化为单个凹痕，该凹点的每个点表示一定的平衡中心，两个横向轴的泛化，它们的相互过渡，即中心轴的形成和旋转运动这样。 有一个全局的通用轴，所有物质都围绕该轴开始旋转，而不是更早的许多径向会聚，离心向心抽吸（图3）。
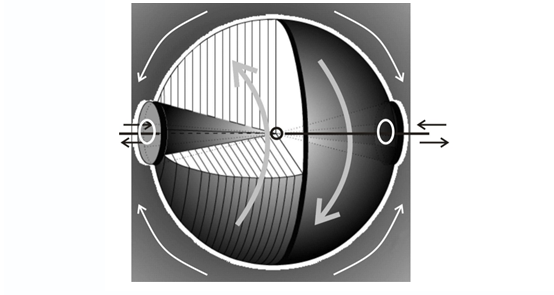图 3.宇宙的一半减半之前的胚胎物质被转换成许多平坦的圆盘运动，在赤道处巨大，并逐渐减少为两个极点，绕指定的轴串起并旋转（在半轴中为相反方向）。 再次，共振现象，现在应用于沿给定轴（向中心并远离中心）以相反方向旋转的半球盘，导致平衡地分成两部分，随后将它们凝聚成两个球，伴随着一个中间壳的溶解，并填补了产生的中间间隙胚胎分裂产品。 这种物质的解决方案可以看作是空间，或者甚至可以更好地用作中值平衡场-SOE，张力，拉直，拉伸，倾向于在一种裂变产物和另一种裂变产物上均等地分层，但是到目前为止，它被迫以多种方式波动。
依此类推，沿着几何级数，会发生胚胎向最内部中央微泡的分层（图4）。 这种级联的转换的结果是，拓扑介质显示为均匀分布在SOE中的大量微气泡，就像在晶格的节点中一样，形成了Universe（SLE）的全局字符串框架。
微气泡的应变立方拓扑结构只能在每个节点中严格在三个相互垂直的平移返回方向上产生脉冲运动。
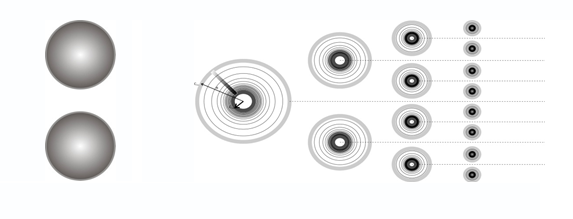图 4.宇宙的胚胎按顺序分为两部分然后按指数划分的图片在这种情况下，物质的运动被严格地渠化，没有其单一的，广义的中心的表现，而是均匀地分布在每个微泡中。 结果，就没有这样的冲动传递的离心向心方向，即，收敛的发散径向以及同心积分的运动类型。 有充分的理由将这种状态（阶段，阶段）限定为平行（并排），完全解压缩的存在形式（图5）。 这是物质三维的明显来源和客观基础。
造成这种情况的重要原因是什么？ 首先，这三个相互垂直且相交的轴平面方向代表基本的，遗传上的节点，最大表达的拓扑基础，它们能够生成，表现出任何其他组合的物质运动，包括将其恢复为原始状态，从而进行拓扑循环。
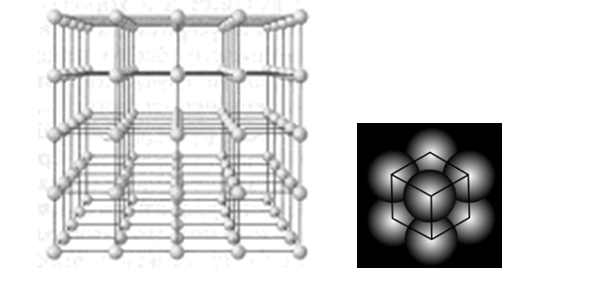图 5.微观气泡在集合（宇宙的弦框架）中以及局部在微观水平上的相互排列的立方形式在这里，有必要阐明与物质从封闭相到开放相的转变相关的运动的特殊性，并进行拆箱。
首先解释。 无论我们如何揭示“运动”概念的内容，我们的意识都会受到质疑，并且需要澄清它仍然在运动：任何物体，以太，空虚，什么都没有？ 这是因为，按照我们的理解，运动不是没有意义的，而且我们根本无法想象“赤裸运动”本身。 因此，有必要再次清楚地指出，运动被理解为整个边界区域的位移，而后者恰好是两个拓扑极性相互作用的产物。 有限和无限的各种比例构成了运动的主题。
第二种解释。 我们证明宇宙的胚胎不会在任何地方移动，但是内部的球形波会在离心向心方向上周期性地循环通过它。 另外，在其中，同时有条件地，顺时针和逆时针地在圆周上绕径向方向进行扫描，总体上表现出各种拓扑极性比率。 在这种情况下，仅发生运动脉冲（惯性）的顺序传输。 因此，胚胎可以由一个单一的“胶状果冻”团块代表，其中充满了上述的中继传递和振动。
第三种解释。 最后，物质的分解，胚胎的分层伴随着看似显着的动力学，但通常意义上没有运动。 有一个解开的，拓扑极性的详细并行排列，简化为一个共同的分母，以统一和离散的形式，自然地表现出最大和最小的完整和极端的表现。 在大量的物质表现中，仅再次观察到了不同形式的干扰。
但是，对运动的这种理解仅在微泡由内而外（离开它们的内部集中状态并将其活动指向外平面）并由此发展出物质的自主微观量子之前，仍然是有效的。 后者表示极性的非常特定的相关性，能够与其他类似的量子相互作用，因此能够以一个速度或另一个速度和一个加速度在一个或另一个方向上显示独立运动。 在这种情况下，我们开始将运动与物质砖块位置的变化联系起来，然后与由它们组成的肿瘤联系起来，在相互运动（变化）的过程中，它们获得了相当确定的形状，大小和其他理化特性。
因此，开放相中的物质表现为两个肿瘤-中位平衡场（SOF）和其中的许多漂浮微泡（SLE）。 从那时起，SOF作为气泡之间的空间，在物理上表现为一种超大的，拉直的，因此非常紧张，展开，全面但仍然有限的肿瘤。 此外，它充满了动态的量化波纹：从巨大的半波（由于宏观胚胎最初的分裂分层成两半，然后沿几何级数逐渐扩展）到内置的先前相对于其中间状态逐步降低的扰动（根据定义）。
物质表现形式的最终外翻阶段物质运动的这一阶段与SCC和SLE从其中平衡状态附近的无限单调脉动的释放，身体向成熟运动的转变，运动创造力，以及上述三维碱基的遗传组合有关。 就此而言，仅需再次展示来自两个方面的平衡努力。
SCS和SCR之间这种相互作用的根源再次是共振-在第一个宏观情况下，SCS振动和弦结构（许多气泡的线性顺序组合）的相应模态的重合，然后在第二个微观情况下与微气泡的自然振动重合。
在第一种情况下，它们导致以最小的差异，收敛而不是严格的平行度和直角形式出现的与脉冲传播的规则立方形状的偏差可忽略不计。 结果，出现了许多均匀分布的区域-环形和椭圆球形的线形拓扑壁ches。 在第二种情况下，与超细微观模态相同的共振现象，即与单纯形中微气泡的固有频率相一致的频率，会导致它们分裂成碎片，将碎片向内翻转，并从中重新装订基本粒子。 并且已经出现的拓扑生态位开始为后者充当随后的物质运动及其加速器的通道（图6）。
换句话说，在显着的拓扑利基内部，运动的粥开始“酿造”-物质的物质形式，与运动的脉冲传递形式完全不同。 物质身体有机会表现出各种类型的运动，具有自己的血统，个体轨迹，自身的形成，合作历史等。 运动中心的创建和泛化，震中（首先是银河系，然后是普遍的）的探索时代开始了。
为了进行这种理解，您需要知道没有外围就没有定义中心，并且在环境之外没有意义。 , , , , , . () , , , . , , .
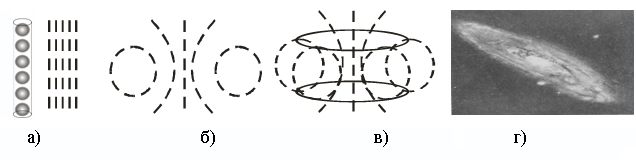
图 6. : ) ; ) ; ) ; )
, , . , , : . ( ) ( ), , . .
. — , , . , , , «». - - , , , .
. ? , - , . , .. , (). , . , , , , . . (, , ) , - ( , 360º) . - .
, , - . , , ( ), , .. () . , . , .
, - .
. - - - , , -, - . : , , , . . , , , ( ) - . , , . . . - .
, , , , . (, , ) . , -, (Hubble Deep Field), . . - . . , .
, . , , . . , , – « », . , . , - , .
, — . , . « », . (, ), .
, , . , - , . – . ? , . ?! , , . , , . , , . , , , . . , , — , . , , , , . . , – .
, , , . — ( ). , . , .
- — , . , , — , , . , , , - .
结论 , - , ( ). - , . - , , - , - , (. 7).
« » , . , , , - — . . (), . , , . , , , . , . . , , ! , – , , , . , .
图 7. -, . , -, , , . . , . .
, - – . , – . , , , , . , – . , , . - - .
. , , . . , «» , , , - , - – . , . , .
«» , - , . , , .
, , ., , «» , , -. - , , : , , . , , , . -, , , . . .
, , . , . , . , .
, . . . , , , , – , , , , , .
: . – , Altaspera. — 2012. -352 . ( ); – – . – .: . — 2017. – 368 .