希格斯字段如何工作：2）为什么希格斯字段平均非零

希格斯场如何工作：

1. 主要思想
2. 为什么希格斯场平均非零
3. 希格斯粒子如何出现
4. 为什么希格斯字段必不可少

自然界中的希格斯场的平均值不为零，而我们知道的自然界中的其他（显然是基本）场的平均值为零是怎么回事？ [非常小的字样：除了最低级别的引力场外，其他字段都称为度量，这使您可以确定空间和时间的存在]。

首先，费米子场本质上不能具有较大的常数非零值。 这是由于费米子和玻色子之间的差异。 玻色子可以平均非零，但费米子不能。 因此，您可以忘记电子（以及它们的近亲介子μ和tau），中微子和夸克。 小字体：费米子可以彼此配对或与反费米子配对并制成复合玻色子，玻色子平均非零。 上夸克和下夸克及其反夸克，以及超导体中的电子都是如此。 但这是一个漫长的故事，它并不直接关系到我们。

光子，胶子，W和Z的场如何？ 这些都是玻色子。 原则上，这些字段在整个Universe上可以具有恒定的非零平均值。 但是实验，而不是理论，说事实并非如此。 足够大的非零电场值会导致出现各种效果，而我们没有观察到。 其中最重要的是大规模违反旋转不变性。 电场是矢量（spin-1），它沿某个方向指示，因此，如果非零，则该值指示的方向应与所有其他方向不同。 （图1，左下方）。


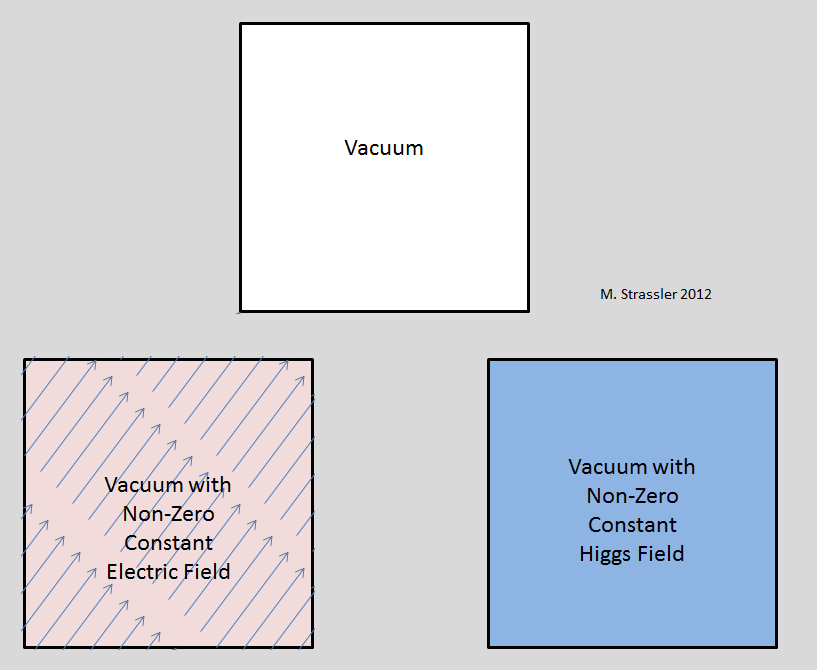图 1个

希格斯（Higgs）字段是标量（spin-0），它不指示任何位置。 在其他标量场（既不是基本场也不是相对论场）中，我们可以举出空气密度场，地球内部的压力场和海洋温度的示例。 在空间和时间的每个点上，密度或压力或温度只是一个数字，而电场是一个数字和一个方向。 因此，如果希格斯字段具有非零值，则不会出现首选方向-图。 1，右下角。 更奇怪的是（因为它是相对论的），希格斯字段不会生成任何首选的参考系。 对于空气密度，有一个首选的参考系统，因为您要么相对于空气静止不动，要么穿过空气。 但是对于希格斯领域来说并非如此。 所有观察者都相对于他休息。 因此，描述各种现象的爱因斯坦SRT的成功并不矛盾非零相对论标量场（例如希格斯场）的存在。 简而言之，在存在非零希格斯场的情况下，真空的行为与在H = 0时的行为完全相同； 它的存在只能通过对粒子质量的影响（或通过更剧烈的变化，例如使用LHC来制造希格斯粒子）来检测。

对于希格斯场，最简单的方法是在整个宇宙中保持非零值，前提是它具有一个非零平衡值H ₀参与其1类运动方程：

$$

$$d ^ 2H / dt ^ 2-c ^ 2 d ^ 2H / dx ^ 2 =-（2 \ pi \ nu_ {min}）^ 2（H-H_0）$$

（应该是1类，而不是0类，原因是在讨论希格斯粒子后我们会明白的原因）。 实际上，情况要复杂一些。 正确的公式如下所示：

$$

$$d ^ 2H / dt ^ 2-c ^ 2 d ^ 2H / dx ^ 2 = a ^ 2 H-b ^ 2 H ^ 3$$

其中a和b为常数（它们的平方为正！请注意² H前面的加号，并将其与上一个方程式中的负号进行比较），我们将在后面学习。 可以重写为：

$$

$$d ^ 2H / dt ^ 2-c ^ 2 d ^ 2H / dx ^ 2 =-b ^ 2 H（H ^ 2-[a / b] ^ 2）$$

如果H（x，t）在空间和时间上是常数，则dH / dt = dH / dx = 0，因此

$$

$$0 =-b2 H（H2-[a / b] ^ 2）$$

（当H（x，t）是x和t中的常数）时，他具有解（目前，我们将大大简化所有内容）：

1. H = 0
2. H = + a / b
3. H =-a / b

换句话说，平衡位置是三个，而不是一个。 细则：我在这里大大简化了它，但不影响其含义。

目前尚不清楚，但是解H = 0是不稳定的。 这种情况类似于图1所示形式的碗中球的运动方程。 2-类似于酒瓶的底部。 他还具有三个平衡位置，一个处于0位置，两个处于±x _0位置 。 但是很明显，位于0的位置是不稳定的-任何推动都会导致红球滚动到x = 0以外，这是这种情况的主要变化。 相反，在x = x ₀处的平衡_是稳定的，因为任何推动都会导致绿色球在x = x ₀点附近以较小的幅度振荡-而不是剧烈变化。 对于x = -x ₀的浅绿色球也是如此。 同样，尽管H = 0将是希格斯场方程的解，但事实证明，我们宇宙的历史非常复杂，无法保证应正确踢希格斯场，因此它不能停留在该位置。 取而代之的是，希格斯字段处于非零值且处于稳定状态的解决方案中。



几十年来，由于实验和理论的结合，我们知道希格斯场（传统上称为“ v”）的值为246 GeV。 这使我们对常数a和b有了一个概念：

a = vb =（246 GeV）b

因此，我们可以确定a到b，然后可以重写希格斯运动方程：

$$

$$d ^ 2H / dt ^ 2-c ^ 2 d ^ 2H / dx ^ 2 =-b ^ 2 H（H ^ 2-v ^ 2）$$

但这并没有给我们b的概念。 在下一篇文章中，我们将了解有关他的更多信息。

现在，尽管我已经做好了一切准备，使得H可以等于v或–v，但是希格斯字段是正数还是负数都没有关系（实际上，还有更多可能性，请参见下文）。 由于没有任何东西取决于H的符号，因此世界将具有完全相同的物理性质。 它并没有立即变得明显，而是； 一个提示-无论您在我描述的方程式中还是在希格斯场的工作原理描述中找到H时，H ²随处可见，不仅H-而且H ²不依赖于H = v或H = -v 。 [小写：实际上，H是一个复数字段，具有实部和虚部，因此H可以等于v乘以任何复数z，其中| z | = 1； 实际上，H * H = | H | ² ，但不取决于z。 甚至还不是全部！ 但是今天足够了。]

如果您找到某种方法（例如，通过在大型强子对撞机上相互碰撞质子）以某种方式将希格斯场推入或引入扰动，则它将来回振荡-也就是说，波以形式出现

$$

$$H = v + A cos [2 \ pi（\ nu t-x / \ lambda）]$$

其中A是波幅，ν和λ是频率和波长，并且ν和λ之间的关系取决于运动方程的确切形式，尤其是b和v。 由于希格斯场是量子，因此这些波的振幅将被量化，这些波的量子就是我们所说的希格斯粒子。 下次我们将考虑这些粒子的特性。